基于FastSLAM的绳系机器人同时定位与地图构建算法
2021-03-27王小涛张家友王邢波韩亮亮
王小涛,张家友,王邢波,韩亮亮
1. 南京航空航天大学 航天学院,南京 210016 2. 南京邮电大学 自动化学院,南京 210023 3. 上海市空间飞行器机构重点实验室,上海 201108
火星和月球表面存在着大量极端地形区域,如陡峭斜坡、松软土壤、高耸悬崖、沟壑等[1],对这些区域的探索可以提供大量有价值的信息[2]。人们提出多种极端地形机器人用于这些地形的探索。按照是否使用绳索,极端地形机器人分为绳系机器人和非绳系机器人。绳系机器人还可以进一步分为绳系腿式机器人(如Dante II[3-4]),绳系轮式机器人(如Cliffbot[5]、TRESSA[6]、Axel[7-8]和vScout[9-11])和绳系履带式机器人等。在绳索的辅助下,绳系机器人能够攀爬陡峭斜坡、高耸悬崖等,可用于完成极端地形区域的探测任务。
在复杂环境中运动时,绳系机器人的绳索会接触并缠绕障碍物,从而在绳索与障碍物之间构成接触点。在返回出发点时,机器人必须沿着与出发路径同伦的路径移动,从而能够按顺序依次解除各接触点,避免出现绳索缠绕现象。人们常采用下列2种绳索管理方法解决绳系机器人的绳索缠绕问题[12],第1种方法是通过机器人运动规划避免绳索缠绕,该方法需要环境地图信息、机器人位置信息以及障碍物位置信息等先验知识,严重限制了绳系机器人的实用性;第2种方法是定位绳索与障碍物之间的缠绕位置,在返回时机器人沿同伦路线运动以解除绳索缠绕。Kumar和Richardson[13]提出绳索缠绕检测方法,利用绳索方位角和绳索张力检测绳索的缠绕位置,在此基础上利用“绳索跟随”法解除绳索缠绕。然而该方法仅利用绳索方位角和张力的不一致性来 “暴力定位”接触点,因此该方法本质上属于避免缠绕发生[14]的方法。Murtra和Mirats[15]融合绳索长度数据、惯性导航单元及轮式里程计数据,利用非线性优化方法解决管道检测机器人的定位问题。该方法仅将绳索长度作为约束条件来提高机器人定位精度,并没有解决绳索缠绕位置的定位问题。
针对绳索缠绕问题,McGarey等[16]利用基于粒子滤波器[17-19]的FastSLAM[20]框架估计绳索缠绕位置,并实现绳系机器人的同时定位与地图构建(Simultaneous Localization and Mapping, SLAM)。McGarey等[21]进一步基于机器人SLAM问题的数学描述[22],提出绳系机器人的TSLAM(Tethered Simultaneous Localization and Mapping)框架,并利用批量处理方法解决绳系机器人的SLAM问题。该方法与视觉SLAM中的光束平差法[23]类似,将最大后验概率估计问题转化为求目标函数最小值的非线性优化问题,但该方法不满足实时性要求,无法在线运行。
针对绳系机器人与障碍物间接触点之间的相关性及机器人运动模型和观测模型的非线性,本文提出基于改进FastSLAM框架的绳系机器人同时定位与地图创建算法。该算法将绳系机器人的SLAM问题分解为机器人位姿估计问题和接触点位置估计问题。利用无迹滤波器估计接触点的位置;利用粒子滤波器计算机器人位姿的后验置信度,并利用观测模型的无迹变换处理来简化粒子权重的更新过程。
1 绳系机器人机械模型
针对极端地形区域的探测任务,设计了绳系轮式机器人,其机构模型如图1所示。绳系轮式机器人的结构部分主要包括2个车轮、1个连接轴体、脚轮臂和绳索等部件,同时还包括车轮、脚轮臂和绳索绞盘相应的驱动传动系统等部分。绳系机器人主要通过电机驱动和齿轮啮合传动的内置绞盘来实现绳索的卷绕和伸展。
绳系机器人装有惯性测量单元来感知自身运动状态。机器人还安装张力传感器,使绳索保持足够张紧状态,实现绳系机器人在陡峭地形上工作的能力。
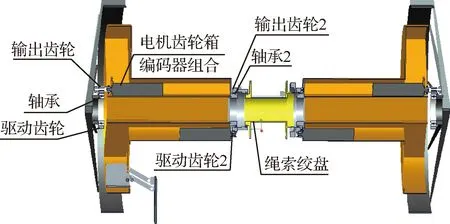
图1 绳系机器人模型Fig.1 Model of tethered robots
2 绳索机器人的运动模型和观测模型
2.1 移动机器人的运动模型和观测模型
当机器人在未知环境中运动时,需要同时解决机器人自身定位和环境地图构建问题,这2个问题相互影响,机器人自身定位影响着地图的观测信息,反过来环境地图又影响着机器人的定位。移动机器人的SLAM问题涉及到机器人运动模型和观测模型。给定t-1时刻机器人的控制输入ut-1和机器人状态xt-1,则机器人的运动学模型可表示为
xt=f(xt-1,ut-1)+wt-1
(1)
式中:f(xt-1,ut-1)为非线性状态转移函数;wt-1为均值为0、协方差矩阵为Qt-1的高斯白噪声。
t时刻机器人对第n个路标点的观测值为
zt,n=g(xt,yn)+vt
(2)
式中:g(xt,yn)为非线性测量函数;yn表示第n个路标点的位置;vt为均值为0、协方差矩阵为Rt的高斯白噪声。
当机器人在二维空间运动时,机器人t时刻的状态可用3维向量xt表示:
(3)
式中:xt、yt为t时刻机器人的位置;θt为t时刻机器人的方位角(机器人移动方向相对于x轴正方向的夹角)。t时刻机器人的运动学模型表示为
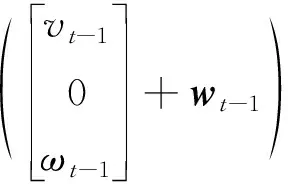
(4)
其中:T为采样时间间隔;vt-1和ωt-1分别为t-1时刻机器人的线速度和角速度。
2.2 绳系机器人的观测模型
在绳系机器人的运动过程中,其绳索与障碍物之间发生接触甚至出现缠绕现象,如图2所示,其中黑色实线表示机器人的移动轨迹,虚线表示机器人未来运动轨迹,箭头表示机器人运动方向,点划线表示缠绕在障碍物之间的绳索部分,点虚线表示当前障碍物与机器人之间的绳索部分。
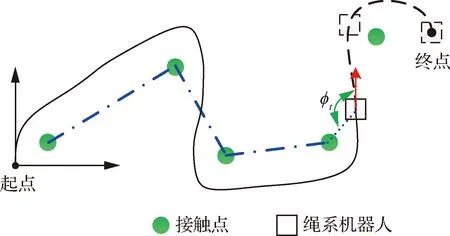
图2 绳系机器人系绳缠绕Fig.2 Tether winding of tethered robots
设t时刻机器人与障碍物之间的当前接触点为第n个接触点,其坐标yn定义为
(5)
式中:xn、yn为第n个接触点的位置坐标。t时刻
接触点的位置可根据机器人当前绳索总长度与方位角测量值计算得到。
t时刻机器人的测量值zt表示为
(6)
式中:dt为t时刻机器人所释放的绳索总长度;φt为t时刻当前接触点和机器人之间绳索与机器人前进方向之间的夹角。
t时刻机器人所释放的绳索由2部分组成:一部分为固定长度的绳索部分dfixed,t,即点划线所表示的接触点之间的绳索部分;另一部分为自由长度的绳索部分dfree,t,即点线所表示的当前接触点与移动机器人之间的绳索部分。由图2可知机器人所释放的固定部分绳索长度为
(7)
机器人所释放的自由部分绳索长度为
(8)
则t时刻机器人所释放的绳索总长度为
dt=dfixed,t+dfree,t
(9)
t时刻机器人和当前接触点间绳索与机器人速度方向之间的夹角φt为
(10)
则机器人观测模型可表示为
(11)
在传统移动机器人SLAM问题中,机器人每时刻可以观测到多个路标点,且各路标点之间是相互独立的。而在绳系机器人运动过程中,其绳索与障碍物之间可能发生接触甚至出现缠绕现象,因此绳系机器人的SLAM问题与传统SLAM问题的区别在于:① 绳系机器人的观测值与所有接触点相关;② 由于绳索的存在,接触点之间不相互独立,如图3所示,其中向量xt(t=1,2,3,4)表示绳系机器人不同时刻的状态。

图3 绳系机器人的SLAM问题Fig.3 SLAM problem of tethered robots
已知t时刻绳系机器人的位姿,当前接触点的坐标可由式(9)和式(11)计算得到:
(12)
由式(12)可知t时刻当前接触点的位置与其他所有接触点相关,如图3所示,其中点虚线表示机器人与当前接触点之间的绳索部分,加粗虚线表示机器人对应的其他接触点。
2.3 绳系机器人SLAM问题描述
绳系机器人的SLAM问题可描述为:根据机器人传感器的测量值和控制信息,计算机器人运动状态和接触点位置的后验概率密度为
p(x,y|z,u)
(13)

机器人运动状态和接触点位置的后验概率分布式(13)可通过2种方法得到:滤波算法和最大似然估计方法。后者需要利用非线性优化方法来解决最大值估计问题,所需计算量非常大,难以在嵌入式设备上实时实现。本文采用滤波算法解决上述绳系机器人的SLAM问题。
因为当前时刻的观测值可能是由当前接触点产生的,也可能是由新接触点产生的,甚至可能是由噪声产生的,因此观测值为多模态分布。扩展卡尔曼滤波算法是基于单峰高斯分布的,不适用于绳系机器人的SLAM问题。粒子滤波可用于非线性、非高斯及多模态概率模型,因此可用于解决绳系机器人的SLAM问题。本文将绳系机器人的SLAM算法分解为用于机器人状态估计的粒子滤波算法和用于接触点位置估计的无迹滤波算法2部分。与McGarey等所提出的基于FastSLAM框架的绳系机器人SLAM算法[16]的不同之处在于:① 利用无迹滤波算法代替扩展卡尔曼滤波算法来估计接触点的位置;② 在机器人状态估计的粒子滤波算法中,用非线性观测模型的无迹变换方法简化粒子权重更新过程。
3 基于粒子滤波的FastSLAM算法
针对绳系机器人观测模型的非线性和多模态特性,本文基于粒子滤波算法和无迹变换提出改进FastSLAM框架来解决绳系机器人的SLAM问题。
3.1 SLAM问题分解
Doucet等[18]提出的Rao-Blackwellized粒子滤波器对联合后验分布的估计问题进行因式分解,可用于高效解决机器人定位和地图构建问题。Montemerlo等[20]将该方法扩展到机器人的SLAM问题,将机器人位姿和路标点位置的联合后验概率分布p(x1:t,y1:k|z1:t,u1:t)的估计问题分解为用于机器人位姿估计的粒子滤波器和基于机器人轨迹的地图创建部分。基于上述思想,绳系机器人的后验概率密度函数也可分解为
p(x|z,u)·p(y|x,z,u)=
p(x|z,u)·p(y|x,z)
(14)
式中:最后一个等式是根据下列假设得到的:接触点位置y只与机器人位姿x和观测值z相关,而与控制输入无关。
一般FastSLAM框架将各个路标点看作是相互独立的,因此p(y|x,z)可分解为各个路标点的后验概率密度函数的乘积[21]。而绳系机器人的观测值与当前时刻所有接触点相关,为了能够利用FastSLAM算法,本文对观测模型进行近似处理:
p(zt|xt,y)≈p(zt|xt,yn)
(15)
式中:yn为当前接触点。式(15)表示观测值只与当前接触点相关,与其他接触点无关,因此式(14)分解为
(16)
其中:N为当前接触点的总数量。
粒子滤波器使用有限的粒子集来近似后验概率密度,其中每个粒子表示一种可能的系统状态。根据式(16),粒子可表示为
(17)

3.2 新接触点检测
在运动过程中绳系机器人可能与新的障碍物发生接触,从而产生新接触点,因此在每一时刻必须判断是否有新接触点产生。新接触点是根据绳索长度测量值和估计值之间的不一致性来确定的,检测方法如图4所示。t时刻绳系机器人与当前接触点之间的距离估计值为
(18)
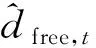
(19)
则表示有新接触点yn+1产生;否则表示没有新接触点产生。
当有新接触点产生时,其位置初始化为
(20)
式中:机器人与新接触点之间的距离d2可由三角形余弦定理计算得到:
(21)
其中:
(22)
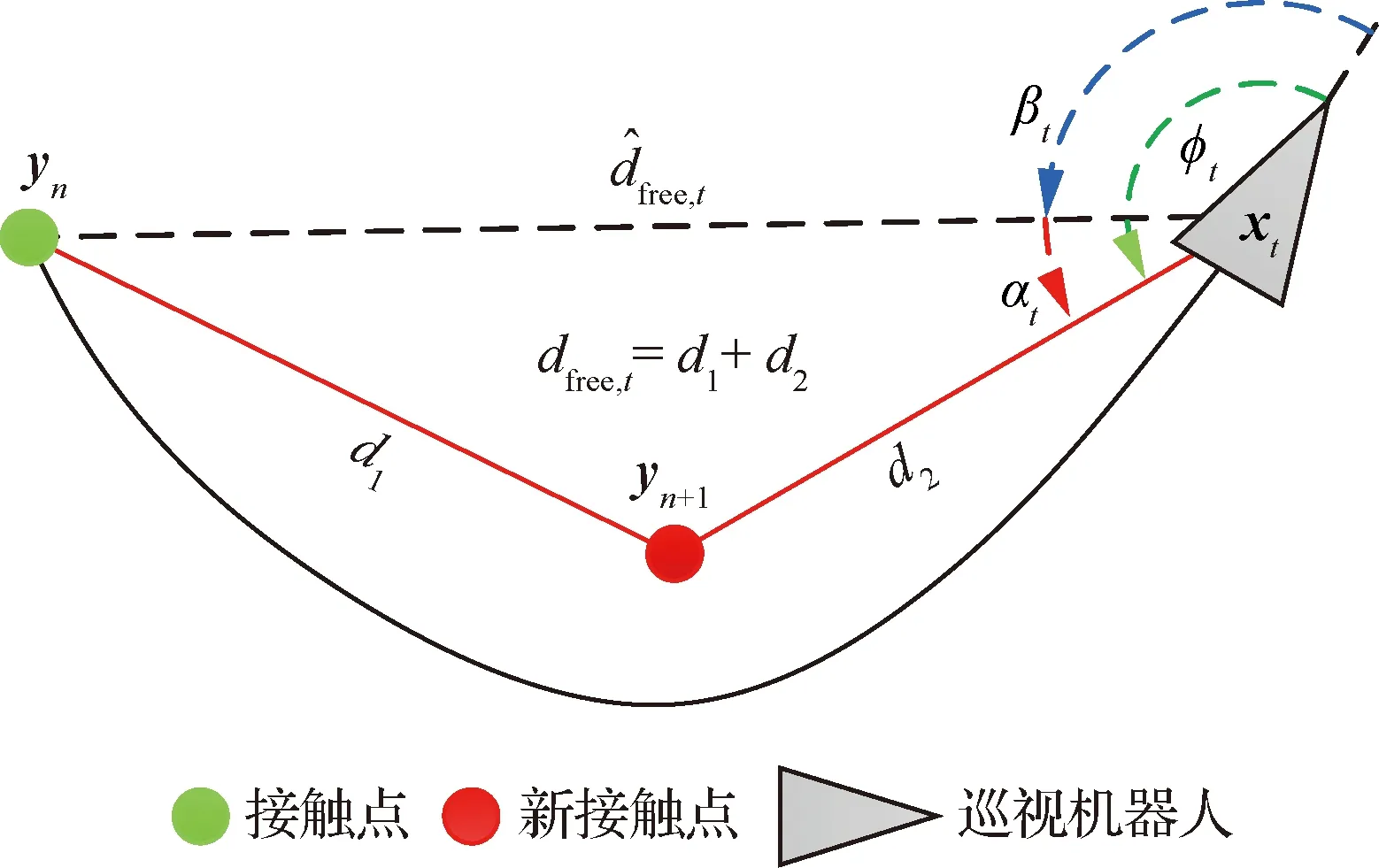
图4 检测新的接触点Fig.4 Detection of new contact point
3.3 FastSLAM算法
FastSLAM算法根据上一时刻的机器人状态后验置信度、控制输入和观测值计算机器人当前时刻的状态后验置信度,并迭代更新接触点的均值和协方差阵,具体步骤如下。
根据t-1时刻的测量值z1:t-1和控制输入u1:t-1预测t时刻的机器人状态xt的置信度:
u1:t-1)dxt-1=
(23)
式中:bel(xt-1)为t-1时刻的机器人状态后验置信度;p(xt|xt-1,ut-1)为机器人运动方程的概率模型。
粒子滤波算法利用有限的粒子集近似后验概率密度,其中每个粒子表示一种可能的系统状态。从先验置信度bel(xt-1)抽取随机样本集为
(24)
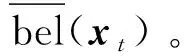
2) 更新接触点均值和协方差矩阵
当没有新接触点产生时,根据贝叶斯准则,接触点的后验置信度更新如下:
p(yn|x1:t,z1:t)=
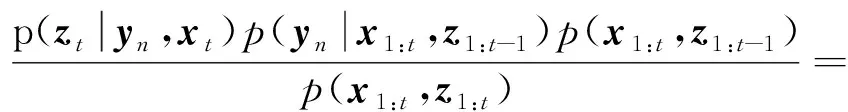
ηp(zt|yn,xt)p(yn|x1:t-1,z1:t-1)
(25)
式中:η表示归一化常数;p(zt|yn,xt)为观测值概率模型;p(yn|x1:t-1,z1:t-1)表示接触点的先验置信度。当没有新接触点产生时,接触点的先验置信度可用t-1时刻的接触点后验置信度代替。
由于观测模型为非线性函数,这里使用无迹滤波方法估计接触点位置,该方法能够极大提高接触点定位精度。根据t-1时刻接触点位置的均值和协方差,无迹变换的2n+1个σ点选取如下:
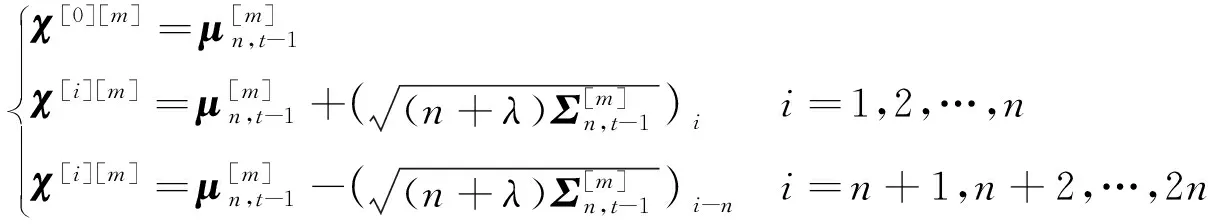
(26)
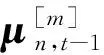
利用观测方程得到2n+1个σ点的观测预测值为
(27)

(28)
其中:权重wg和wc的计算公式为

(29)
其中:β=2。
基于当前时刻观测值zt,利用卡尔曼滤波增益更新地图中接触点的均值和协方差矩阵:
(30)
其中卡尔曼滤波增益矩阵计算式为
(31)
当机器人绳索与障碍物之间产生新接触点时,接触点位置均值和协方差的初始化可通过无迹变换方法得到:
(32)
式中:zt为当前观测值;Rt为观测值噪声协方差阵;g-1(·)为测量方程的逆。则新接触点的均值和协方差矩阵为

(33)

3) 计算粒子权重
利用当前时刻的所有控制输入和测量值,计算当前时刻机器人状态xt的后验置信度:
bel(xt)=p(xt|z1:t,u1:t)=
(34)
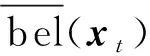
(35)
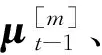
利用无迹变换方法对观测模型进行线性化处理,可以得到式(35)的闭式解。此时粒子权重为
(36)
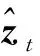
(37)
由于部分粒子的权重非常小,它们所表示的状态的可能性非常低,保留这些粒子并不会对系统有显著的性能改善,因此需要对粒子集进行重采样。重采样后的粒子集为
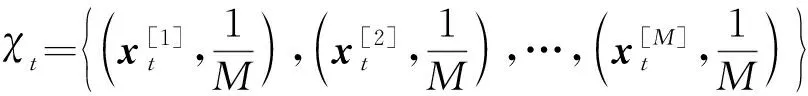
(38)
此时每个粒子具有相同的权重,新粒子集不包含权重较低的粒子。一般来说,不需要在每次迭代过程中都执行重采样,典型方法是根据粒子的有效性Neff来确定是否进行重采样[24],Neff的计算式为
(39)
当Neff低于设定阈值时,进行粒子集重采样。
综上所述,整个算法流程如图5所示。
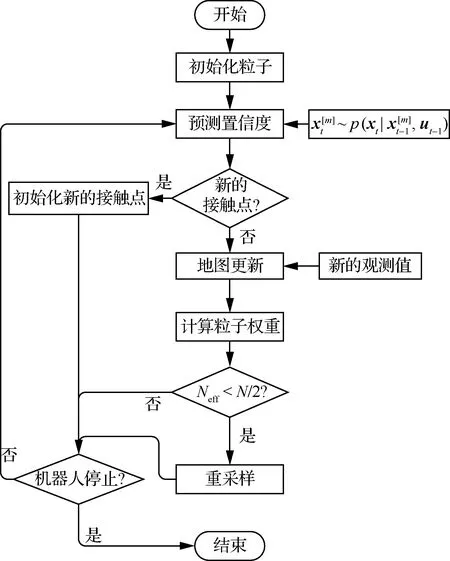
图5 所提算法流程图Fig.5 Flow chart of the proposed algorithm
4 仿真实验
本节利用Monte Carlo仿真实验来验证本文所提出的基于FastSLAM框架的绳系机器人SLAM算法的性能。设仿真步长为0.01,仿真步数为500。绳系机器人的初始坐标为(0,1),绳索固定于(0,0)点。机器人携带传感器测量其所释放绳索长度和绳索与机器人前进方向之间的夹角,假设每个传感器的测量噪声为均值为0.003、协方差为0.002 5的高斯白噪声。绳系机器人在二维平面内沿规划路径运动,在每一时刻利用传感器检测绳索长度和方位角信息,并利用不同算法估计接触点位置和机器人运动轨迹。
利用里程计和本文提出的绳系机器人SLAM算法得到的机器人运动轨迹分别如图6所示。其中三角形表示所给定的机器人与障碍物之间的接触点位置,虚线表示机器人的规划轨迹(真实轨迹),点划线表示基于里程计得到的机器人估计轨迹,实线表示基于本文算法得到的机器人估计轨迹。由图可知,基于本文算法得到的机器人估计轨迹比利用里程计得到的机器人估计轨迹更接近机器人真实轨迹,所以本文算法可有效估计机器人的运动轨迹。
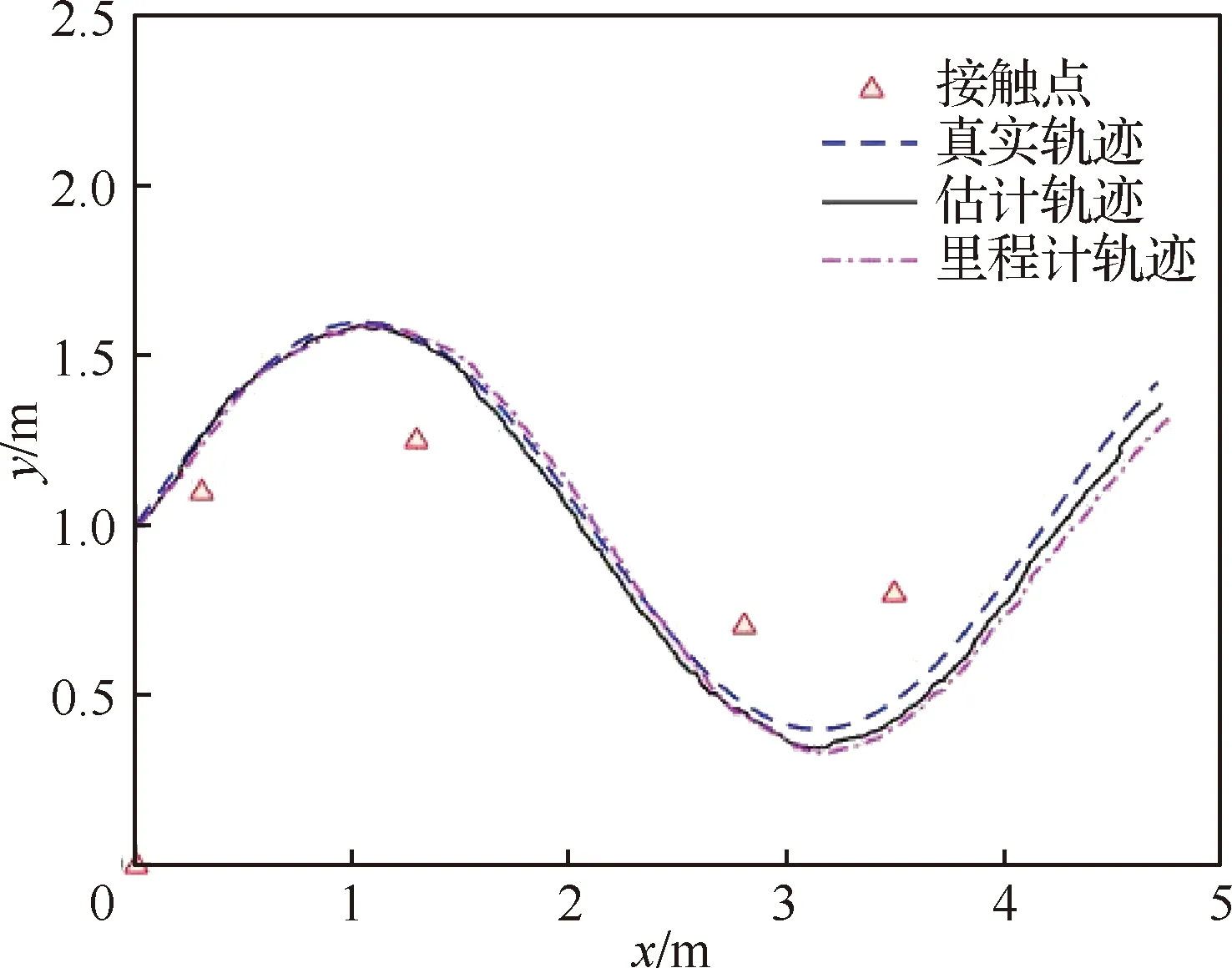
图6 绳系机器人的运动轨迹及其估计Fig.6 True and estimated trajectories of tethered robots
当绳系机器人沿规划路径运动时,其绳索与障碍物发生接触并构成接触点。绳系机器人的绳索在接触点之间的分布状况如图7所示,其中三角形表示接触点位置,虚线表示机器人的规划轨迹,实线表示机器人从起点运动到终点后绳索状况。圆点表示利用本文算法得到的接触点估计位置。由图7可知,接触点估计位置逐渐收敛到接触点真值附近,表明本文算法可有效地定位接触点位置。

图7 机器人系绳的轨迹Fig.7 Tether trajectory of robots
本文对里程计方法、McGarey算法[16]和本文算法的估计性能进行了比较。利用这3种算法得到的绳系机器人位姿估计均方根误差RMSE (Root Mean Square Error)如图8所示,其中PF+UKF表示本文所提出的绳系机器人SLAM算法,PF+EKF表示McGarey所提出的绳系机器人SLAM算法。仿真结果表明:本文算法比其他2种算法的估计性能更好。主要是因为本文的绳系机器人SLAM算法采用无迹滤波算法代替扩展卡尔曼滤波来估计接触点位置。该方法提高了接触点的位置估计精度,进而改善了机器人位姿估计精度。

图8 不同算法得到的绳系机器人位姿的估计误差Fig.8 Estimated errors of different algorithms for tethered robots pose
本文还对McGarey的绳系机器人SLAM算法和本文的绳系机器人SLAM算法的运行时间进行比较。本文算法单步执行时间大约为0.071 8 s,McGarey算法单步执行时间大约为0.073 1 s。本文算法的计算复杂度较低,主要因为McGarey算法在粒子滤波重采样过程中将每个粒子分裂为3个副本。而绳系机器人在每一时刻只有一个当前接触点,McGarey算法产生了大量冗余重复粒子,这种冗余随着时间推移逐渐加重,降低了粒子的多样性,增加了计算复杂度。
5 结 论
基于无迹变换和粒子滤波算法,提出利用FastSLAM框架解决绳系机器人的同时定位和地图创建问题。该算法利用无迹滤波估计接触点位置;利用粒子滤波估计机器人位姿,并利用无迹变换简化粒子权重更新过程。仿真结果表明本文算法可有效估计绳索与障碍物之间接触点的位置、提高机器人位姿估计的精度,而且降低了计算复杂度。但本文提出的绳索机器人SLAM算法具有以下局限性:
1) 在运动过程中绳索需要保持拉紧状态,因此该算法仅适用于2D场景。
2) 假设机器人与障碍物之间的接触为点接触,不影响绳索长度。
在后续研究中,将进一步考虑没有上述局限的机器人SLAM算法;利用多传感信息融合方法改善机器人和接触点定位精度;将绳系机器人应用于实际场合。
