基于干扰观测器的柔性空间机器人在轨精细操作控制方法
2021-03-27刘璟龙张崇峰邹怀武李宁吴琳娜
刘璟龙,张崇峰,邹怀武,李宁,吴琳娜
1. 上海宇航系统工程研究所,上海 201109 2. 上海市空间飞行器机构重点实验室,上海 201109 3. 上海航天技术研究院,上海 201109
近年来,空间作业任务越来越复杂,其要求也越来越高。为了把航天员从危险的外太空操作任务中解放出来并排除人为操作的失误率,空间机器人的使用越来越频繁,其应用前景也越来越广阔[1]。这些机器人根据功能划分,可分为观测机器人、搬运机器人、精细操作机器人等[2](如图1所示)。其中,精细操作机器人多用于完成螺钉旋拧、接插件插拔等拆装任务,对末端操作的精细程度提出了很高的要求[3-6](如图2所示,图中可移动基座系统(Mobile Base System, MBS)是加拿大Ⅱ臂的基座平台,该移动服务系统还包括一个空间站远距离机械臂系统(Space Station Remote Manipulator System, SSRMS)和一个特殊用途灵巧机械臂(Special Purpose Dexterous Manipulator, SPDM))。

图1 在轨组装任务Fig.1 On-orbit assembling task

图2 在轨服务任务Fig.2 On-orbit service task
以太空维修任务中的螺钉、电连接器的操作为例,通常要求关节角精度优于0.01°,末端位置精度优于1 mm,末端姿态精度优于0.5°,对准接触下的力柔顺精度优于2 N和1 N·m。空间精细操作机器人通常具有关节刚度低、摩擦及操作接触力非线性强等特征,这些特征会造成机械臂关节角跟踪精度降低、甚至发散,而关节角的静态和动态误差会逐步累积,最终影响末端跟踪精度。串联空间机器人(机械臂)是多输入多输出系统的典型代表,由于多体系统动力学、关节与电机之间不可忽略的柔性、未建模动态等,使得这类系统的控制变得更加困难。


图3 柔性关节机器人的关节位置PD控制Fig.3 Flexible joint robot PD joint angle position control
针对以上问题,本文提出了一种基于非线性干扰观测器和动力学极点配置相结合的柔性机器人在轨精细操作控制方法。将柔性机器人的关节角位置控制问题转化为两个子问题。内环为柔性关节机械臂的关节力矩环设计,外环为柔性关节机械臂的关节位置环设计。实际工程中传感器的信号较少,内环系统的非线性动态很难获得。针对此问题,本文引入了一类非线性干扰观测器(Nonlinear Disturbance Observer, NDO),可有效准确地估计除输入项之外的集总干扰。若将其作为内环控制律的补偿信号,可有效提高内环系统的鲁棒性。
1 问题描述
一般将柔性机器人分为两类:一类是具有分布式柔性的机器人,称作柔性杆机器人;另一类是指关节处具有集中柔性的机器人,称作柔性关节机器人[13-14]。从本质上看,无论是杆件柔性还是关节柔性都给机器人引入了额外的自由度。其中,杆件柔性更是将原本有限的自由度扩展为无限的自由度。关节柔性的建模主要是基于Spong模型[15]。在此基础上,Farid和Lukasiewicz将杆件柔性引入到模型中,并将关节柔性和杆件柔性对系统的影响进行了对比,得出了关节柔性更突出的结论[16]。本文研究的机械臂,由于其臂杆的基频较高,所以不考虑臂杆柔性,仅对具有刚性杆柔性铰的空间机器人的在轨精细控制问题作深入分析。
可以将柔性关节机器人的动力学模型简化为
(1)

(2)
式中:第1个微分方程为关节动力学方程,第2个微分方程为电机动力学方程,第3个方程为等效关节柔性方程,参考Spong的假设,将关节柔性等效为一个介于电机转角(θ)与关节的实际转角(q)之间的无惯量无阻尼的线性扭转弹簧。此等效弹簧所产生的力矩既是电机动力学方程的反作用力矩,又是关节动力学方程的驱动力矩。系统中存在的其他不确定项(如外力矩项),可与阻尼项、摩擦项一同考虑,都视为集总干扰。由式(2)可以看出,各状态间的相互耦合、各通道中的非线性项使得柔性关节机器人的动力学控制更加复杂。因此,如何解耦变量和增强控制器鲁棒性是设计的难点和关键。
根据时标分离原理和奇异值摄动原理[17],把非线性系统中诸多状态划分为快慢程度不同的状态组而分别进行控制器的设计。实际工程中,由于有柔性的作用,关节角的调节时间一般都会慢于电机转角或者电机力矩的调节时间,所以可以应用上述原理将系统的状态进行分组来分别设计控制器。本文选择关节力矩作为快子系统的状态,而关节角作为慢子系统的状态,将式(2)变形为
(3)
式中:
式(3)中,关节角微分方程中的惯性参数和摩擦可由动力学参数辨识得到。关节力矩微分方程中的关节刚度可由刚度测试实验获得,a、b项可计算得到。为了克服外扰和未建模动态,需要设计专门的估计器或观测器。关节力矩微分方程中的g项只由关节刚度和电机惯量决定,可以认为是已知项。
2 精细操作动力学控制

图4 所提方案的整体原理图Fig.4 Overall schematic diagram of proposed scheme
2.1 非线性干扰观测器的设计
通常来说,广义的干扰观测器技术不仅指对外部扰动的估计,而且还包含模型不确定性影响下的内部扰动的估计[18]。假设一个系统的动态方程表示为
(4)
式中:A、Bu、C、Du表示实际情况下的系统矩阵,令Bd、Dd分别为相应维数的单位阵。用标称参数可将式(4)重写为
(5)
式中:An、Bn、Cn、Dn表示标称情况下的系统矩阵,dlx、dly分别表示状态方程中的集总干扰和输出方程中的集总干扰。令Bld、Dld也为相应维数的单位阵。比较式(4)和式(5)可得:
(6)
由式(6)可知,dlx、dly是包含了模型摄动和外扰的集总干扰。干扰观测器的设计目标就是利用输入、输出和状态信息来估计集总干扰dlx和dly。其中,dly的估计可直接由式(5)得到:
(7)
对于式(5)可以设计如下的非线性干扰观测器(NDO)来估计式(5)中的集总干扰dlx:
(8)
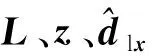
令该干扰观测器的误差为
(9)
则可以证明如下:
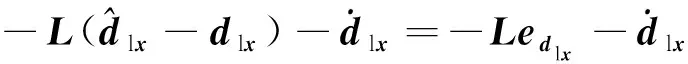
(10)

由2.2节可知,可将式(13)重写为
(11)

(12)
2.2 柔性关节机械臂关节力矩环设计
由第1节所述,将电机力矩作为输入,将关节力矩作为输出,考虑模型摄动、参数漂移和外部扰动,则柔性关节的关节力矩微分方程可表达为
(13)
式中:Δτ为电机动力学模型摄动。此处,认为电机力矩的控制律由两部分组成:
τm=τm0+τm1
(14)
式中:τm0、τm1分别为电机力矩控制律的标称项和扰动补偿项。首先,设计电机力矩的标称控制律,使状态达到理想动态。其次,设计电机力矩的扰动补偿控制律,能够抵消关节力矩微分方程中的aτ+b+Δτ项。
定义关节力矩误差项:
eτ=τd-τ
(15)
设计电机力矩的标称控制律为
(16)

设计电机力矩的扰动补偿控制律为
(17)

若将式(14)代入式(13)中,可得
(18)
由极点配置原理可知,当c2、c3均为正数时,若采用控制律式(16),则关节力矩环闭环系统渐进收敛。
2.3 柔性关节机械臂关节位置环设计
由第1节所述,将关节力矩作为输入,将关节角位置作为输出,则柔性关节的关节位置微分方程可表达为
(19)
式中:Jl为柔性关节的惯量矩阵;Cl为包含哥氏项和离心力项的阻尼矩阵;Δq为关节动力学模型摄动。与2.2节类似,可以设计一个综合控制律τ,使闭环系统既能满足理想的动态又能补偿掉所有未知的不受控的集总干扰。Δq可由干扰观测器测量得到,也可将其视为关节角动力学方程的摄动项(由一次项和常数项组成),可由动力学参数辨识得到。假设动力学参数辨识准确,则式(19)中,各参数已知。
此处,认为关节力矩的控制律由两部分组成:
τ=τd=τ0+τ1
(20)
式中:τ0、τ1分别为关节力矩控制律的标称项和非线性补偿项。定义关节位置误差为
eq=qd-q
(21)
设计关节力矩的标称控制律为
(22)

设计关节力矩的非线性补偿控制律为
(23)
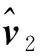
(24)
由极点配置原理可知,当c0、c1均为正数时,若采用控制律式(22),则关节位置环闭环系统渐进收敛。
2.4 二阶低通滤波器的设计
为了求解某指令信号的零阶平滑信号、一阶微分信号和二阶微分信号,本文还设计了两个二阶低通滤波器[19-21]。其中,内环指令滤波器设计为
(25)
外环指令滤波器设计为
(26)
式中:ξ1、ξ2、ωn1、ωn2分别表示内环和外环指令滤波器的阻尼比和自然角频率。为了让内环指令的响应速度更快,令ωn1>ωn2。
3 仿真验证
3.1 关节角控制仿真验证
为验证本文所述方法的正确性和有效性,以某四自由度柔性空间机器人在轨维修任务为例,其标称参数如表1所示,动力学模型及参数定义可参考文献[14]。对其进行关节角位置精细控制,示意图如图5所示。按照本文所提方法,设计了基于干扰观测器和动力学极点配置的控制仿真实验。

表1 本实验采用机器人的标称参数[14]Table 1 Nominal robot parameters in this paper[14]

图5 4自由度柔性空间机器人在轨维修示意图Fig.5 On-orbit maintenance diagram of 4DOF flexible joint space robot
参考式(2)建立电机动力学和关节动力学模型,此处模型假设为杆件刚性、关节柔性,将关节摩擦等效到电机端,考虑电机端摩擦和其他外扰,将电机摩擦f、关节动力学模型摄动Δq、电机动力学模型摄动Δτ分别指定为
(27)
用MATLAB/Simulink仿真3 s,令关节1在0.5 s时刻跃变为1°,令关节2在0.6 s时刻跃变为1.2°,令关节3在0.7 s时刻跃变为1.4°,令关节4在0.8 s时刻跃变为1.6°。其中,如2.4节所述,为了使所有的指令能够平滑变化,将两个指令滤波器的参数设置为
(28)
为了与不含干扰观测器的两环动力学极点配置控制仿真进行对比,外环控制器的结构和参数均不变,本文对内环不含扰动补偿控制律的情况进行了仿真。仿真结果如图6和图7所示。

图6 无干扰观测器时关节1-2位置跟踪对比Fig.6 Comparison of joints 1-2 position tracking without disturbance observer

图7 无干扰观测器时关节3-4位置跟踪对比Fig.7 Comparison of joints 3-4 position tracking without disturbance observer
如图7所示,由于4号电机的非线性摩擦f4=-40 N·m较大且为常值,故当控制律中不含扰动补偿项时,传统的控制律至多只能保证收敛,但还会产生一个较大的稳态误差。相反,由于3号电机的非线性摩擦f3=30 N·m为正值,故关节3的实际角位置输出q3为负偏差。如图6所示,同理可分析关节1的实际角位置输出q1为负偏差,关节2的实际角位置输出q2为正偏差。所以,在内环同时含有未知的电机摩擦f和电机动力学摄动Δτ时,由于内环只有标称控制律,无法补偿掉集总干扰aτ+b+Δτ产生的影响,在此情况下其实际信号并不能准确跟踪理想指令。换言之,这样的控制律在同时含有未知电机摩擦f和未知的电机动力学摄动Δτ时,并不能满足要求。
本文所述方案的仿真结果如图8~图11所示,在内环同时含有未知的电机摩擦f和电机动力学摄动Δτ时,内环所有通道的集总干扰都能快速、准确地被估计,并直接补偿到内环控制律中,使得外环和内环的指令都能被准确跟踪。其中,由于仿真中假设3号和4号电机的非线性摩擦都较大,而关节4除了自身因素外,还受关节3的影响,所以初始时刻,需要内环产生的电机力矩控制量较大,初始的关节4的位置偏差和关节4的关节力矩偏差都较大,但是非线性干扰观测器和干扰补偿控制律迅速产生作用,使得该位置偏差在0.1 s左右就迅速衰减,故对任务执行所产生的影响很小。后续跟踪平稳准确。实验证明,4个关节角位置动态响应的超调均为0,其关节角位置精度均优于0.01°,满足在轨精细操作的要求。本实验证明了本文所提方案的正确性和有效性。

图8 基于干扰观测器方案的关节位置跟踪Fig.8 Joint position tracking with disturbance observer

图9 基于干扰观测器方案的关节力矩跟踪Fig.9 Joint torque tracking with disturbance observer

图10 内环集总干扰关节1-2估计Fig.10 Joints 1-2 lumped disturbance estimation in inner loop

图11 内环集总干扰关节3-4估计Fig.11 Joints 3-4 lumped disturbance estimation in inner loop
3.2 末端柔顺控制仿真验证
为使末端工具在接触环境之后能够适应环境,并验证本文方法与柔顺控制的兼容性,本文另设计了关节空间基于位置的阻抗控制策略。为使末端轨迹运动更直观,本文还进行了关节角驱动正运动学的仿真实验。其中,将环境刚度设置为Ke=104N/m,末端的z向位置由0.1 m处运动到0.063 9 m处附近,假设0.07 m处接触环境,由此产生的环境力由Fe-z=Ke(0.07-yz-actual)计算。简单起见,只在z向受平移力,则将笛卡尔空间六维环境力向量(三平移三扭转)定义为Fe=[0 0Fe-z0 0 0]T。由于任何机器人执行都是在关节空间中执行的,还需要利用δτd=JTFe,将笛卡尔力转换为关节空间的力。最后通过目标阻抗关系式,将关节力矩指令增量映射为关节角指令增量,补偿到原有的关节角指令中。
(29)
下面将带柔顺控制的实验结果与其他结果做比较,仿真结果如图12~图16所示。
图12~图15的图例中,下标d表示理想末端位置指令,下标2Dyna表示传统的两环动力学控制,proposed表示本文所述方案不带柔顺控制,proposed with compliant表示本文所述方案带柔顺控制。图16的图例中,下标τd1-C表示带柔顺控制的关节力矩指令增量。如图12所示,由于4个关节角指令在1.75 s附近叠加了非零的柔顺控制补偿指令,使实际关节角减小了原本的偏转幅度。如图13所示,带有柔顺控制的基于干扰观测器的方案,不但能够补偿扰动的影响,还能使末端根据实际环境约束来调整关节角指令的大小,以改变末端实际位置。如图14所示,假设在0.07 m时接触环境,产生环境力,然后柔顺控制策略起作用,使末端z向位置稳定在0.07 m处。如图15和图16所示,柔顺控制策略使得因接触环境而产生的笛卡尔空间z向力和关节空间的关节力矩都迅速减小。

图12 带柔顺控制的基于干扰观测器的关节位置跟踪Fig.12 Joint position tracking with DO and compliance control
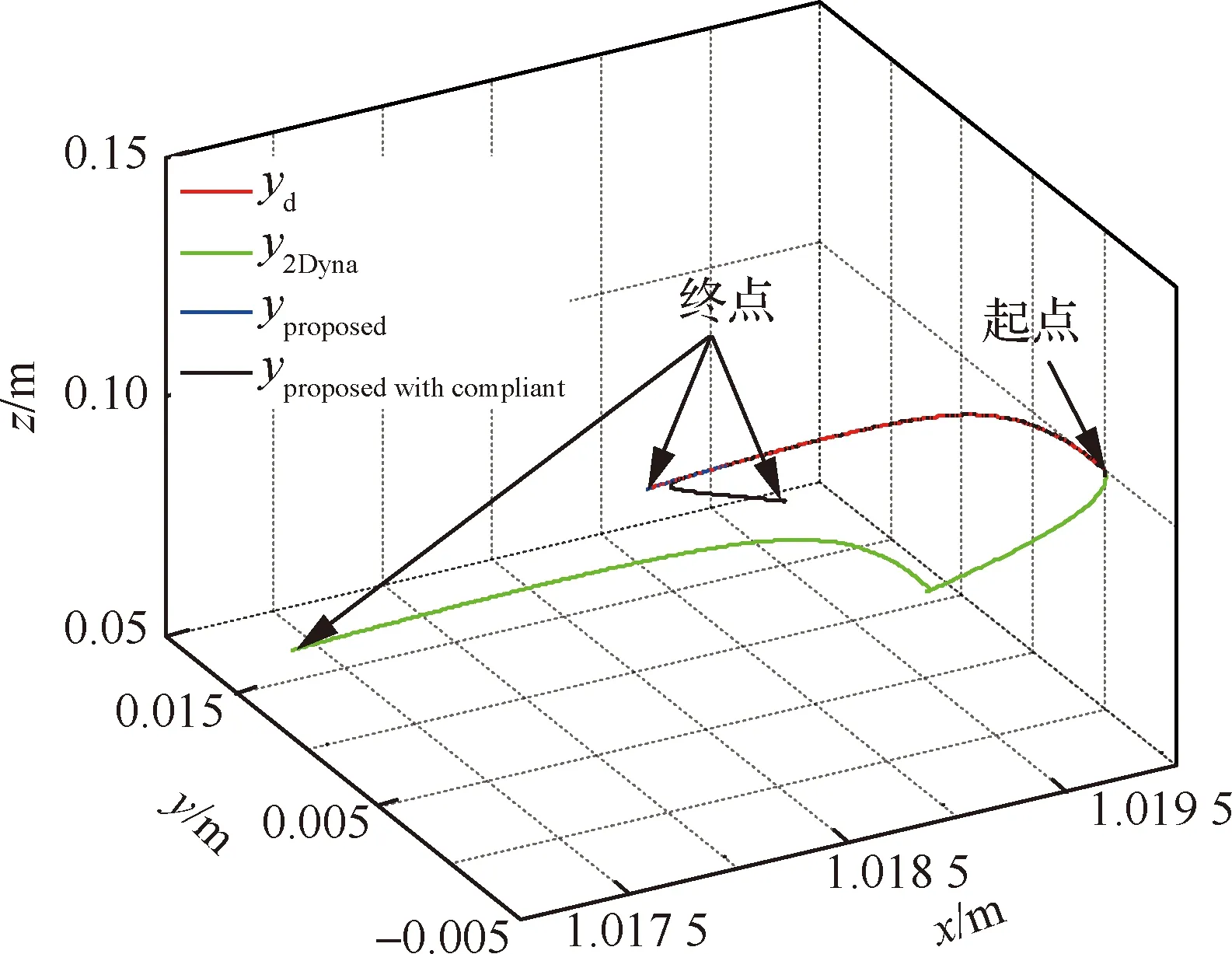
图13 末端位置跟踪对比Fig.13 EE position tracking contrast

图14 末端z向位置跟踪对比Fig.14 EE z axis position tracking contrast

图15 末端z向接触力对比Fig.15 EE z axis force tracking contrast

图16 柔顺控制补偿关节力矩指令对比Fig.16 Joint torque command compensation with compliance control
4 结 论
本文针对空间机器人在轨精细操作控制中遇到的模型摄动、柔性激振引起的PID控制困难等问题,建立了柔性关节空间机器人的数学模型,提出了一种基于非线性干扰观测器和动力学极点配置相结合的方法,并对干扰观测器的收敛性进行了证明。关节角控制仿真实验表明,本文所述关节角控制策略可准确抵消内环干扰对标称模型的影响,并使关节力矩误差为零且关节角位置精度满足要求。末端柔顺控制仿真实验表明,本文所述柔顺控制策略可使末端工具在接触环境之后迅速适应环境,并使末端接触力和末端位置满足精度要求。后续工作将对Δq不为0时,动力学辨识不够准确的情况进行分析,试图用非线性干扰观测器来估计出外环的集总干扰,以使整体方案具备更好的鲁棒性。
致 谢
感谢上海市空间飞行器机构重点实验室和空间结构与机构技术国防科技重点实验室对本文研究的大力支持。
