轮地力学模型参数灵敏度分析与主参数估计
2021-03-27周如意丰文浩邓宗全高海波丁亮李楠
周如意,丰文浩,邓宗全,高海波,丁亮,李楠
哈尔滨工业大学 机器人技术与系统国家重点实验室,哈尔滨 150080
星球车作为典型的轮式移动机器人,不仅在深空探测领域发挥着关键作用,还是移动控制的重要研究对象。由于星球表面的地形松软崎岖,多辆星球车曾发生车轮打滑或沉陷事故。为了改善这种情况,提高星球车的移动性能,考虑轮地相互作用的控制算法[1-2]受到了广泛的关注和研究。地面力学参数是轮地相互作用模型的重要组成部分,对星球车的控制效果具有直接影响。但由于载荷的限制,星球车几乎无法搭载测量星壤力学特性的专用设备[3-4],大部分地面力学参数无法通过直接测量获得,因此地面力学参数的准确估计已成为限制控制算法应用的关键。主流的地面力学参数估计方法以轮地相互作用模型为基础,但该模型形式复杂,参数众多,通常无法同时对所有参数进行准确辨识。因此,对轮地相互作用影响较大的主导参数进行实时估计,以反映地形变化情况,对非主导参数进行在线调整,以提高参数精度,成为支持实时控制的一种折衷办法。
为了筛选出模型的主导参数,通常需要分析参数的灵敏度。在地面力学领域,一般采用局部分析法求解地面力学参数的灵敏度。Li等[5]采用直接求导法分析了地面承压特性模型和剪切特性模型中参数的灵敏度,结合参数取值获得模型的主导参数。但局部分析法只能求解参数在值域内某点附近的局部灵敏度,当输入变量的变化处于不同量级时或模型具有非线性特性时,对应的灵敏度分析能力有限。而全局灵敏度分析方法对分析较复杂的模型具有较大优势,已有多种全局灵敏度分析方法被提出,如Morris方法[6]、Sobol方法[7]、傅里叶幅值敏感性测试[8]等,并广泛应用于水文模型分析[9]和工程结构分析[10]等领域。邓宗全等[11]采用数值法分析了车轮沉陷量,驱动阻力矩和挂钩牵引力对土壤参数变化的敏感程度,得出土壤承压特性参数主要对车轮沉陷量产生影响,土壤剪切特性参数对驱动阻力矩和挂钩牵引力的影响较大,轮地作用对于接触角系数的变化不敏感等定性的结论。
由于地面力学参数较多,利用轮地作用力学平衡方程一般无法直接求解所有参数值,通常利用不同工况(例如不同滑转率)下的车轮状态数据迭代优化求解。Ding等[12]推导了封闭形式的地面力学参数解析解耦方程,并提出将地面力学的8个参数分为3个阶段逐步进行求解的在线辨识方法。Hutangkabodee等[13]使用复合辛普森法则代替轮地相互作用模型中应力的直接积分,简化了轮地相互作用模型,并采用广义牛顿-拉夫森方法实现了地形参数的实时辨识,所提出的方法在车轮牵引力预测中得到运用。Song等[14]根据车轮受到的垂直载荷和电机驱动力矩,采用递归神经网络分别对地面承压特性和剪切特性参数进行了自适应辨识。Xue等[15]使用了多输出最小二乘支持向量机,在不需要测量车轮沉陷量的情况下,利用车轮滑转率、载荷和转矩等信息完成了地形剪切特性参数的在线预测。为了进一步提高参数估计的实时性,适应实时控制的需求,部分工作通过推导解析模型进行实时参数估计。Iagnemma等[16]通过线性化应力公式简化了轮地作用模型,并推导出松软地面下土壤内聚力和内摩擦角的解析表达式,用于在线计算土壤参数。Li等[5]利用三角函数拟合车轮的应力分布以简化传统的轮地相互作用模型,并提出了一种具有容错开关的鲁棒卡尔曼滤波器用于模型中的主要参数实时估计,所提出的估计方法能够快速适应土壤类型的变化。其后在此基础上又提出了地形参数估计的双层结构[17],内层实现主导参数的实时更新,外层采用递归高斯-牛顿算法对所有参数进行调整,提高了估计结果的精度。
总体来说,现有面向轮地力学模型的参数灵敏度分析以局部分析为主,且局限于定性层面,缺乏面向全局的定量分析研究。多数参数估计方法依赖于不同工况下的状态数据,且以地面性质均一稳定为假设。不同工况通常需要人为变换车轮控制策略,难以满足控制实时性需求,均质地面假设在实际应用中也较难满足。因此,亟需面向轮地相互作用模型开展地面力学参数的全局灵敏度定量分析,筛选出主导参数并提出对应的估计方法,为实时控制奠定基础。
区别于定性的参数灵敏度分析和工况要求苛刻的全参数估计方法,本文的主要贡献为:创新地引入了Sobol分析方法,定量地分析了轮地相互作用模型中地面承压特性参数和剪切特性参数的全局灵敏度,为主导参数选取提供了更可靠的依据;推导了解析形式的主导参数估计模型,仅通过单一工况下的状态数据估计主导参数以反映地面承压和剪切特性变化。所提出的主参数估计方法适用于多种滑转工况,且估计结果可用于牵引力预测,以提高星球车控制的安全性和稳定性。
1 考虑轮刺效应的轮地相互作用模型
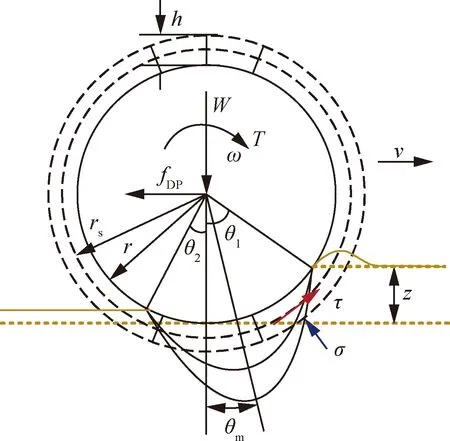
为了增强星球车的移动性能,通常在星球车车轮轮周安装轮刺以提高其牵引能力。例如机遇号火星车,其车轮轮周均匀排布着截面较小的竖直型轮刺。星球车在平坦地面上平稳运动时,轮地接触区域的相互作用如图1[12]所示。图中,ω为车轮转速;v为车轮前进速度;z为车轮沉陷量;r为车轮半径;h为车轮轮刺高度。
车轮所受到的外力包括竖直方向的垂直载荷W,水平方向的前进阻力fDP,电机的驱动力矩T和土壤对车轮的作用力。松软土壤对车轮的作用力表现为连续的正应力σ和剪应力τ,分布情况受到车轮进入角θ1和车轮离去角θ2的影响,且在θm处产生最大应力。由于轮刺的存在,当车轮转动时,车轮轮周表面与土壤的摩擦转变为土壤与土壤之间的摩擦,并可等效为以等效剪切半径rs(图1中虚线所示)作用于车轮,对应的剪切应力相较于光轮情况显著增加。应力的微观作用通过积分表现为宏观上的力和力矩,即法向力FN、挂钩牵引力FDP和驱动阻力矩MR。
星球车的行驶速度较低,其稳定行驶时各时刻车轮的运动状态可视为准静态。不考虑车轮侧偏,可通过应力积分列写平衡方程[12]:
(1)
式中:b为车轮宽度;θ为轮地作用角;σ1和τ1分别为车轮前部分的正应力和切应力;σ2和τ2分别为车轮后部分的正应力和切应力。当轮刺高度为h时,等效的剪切半径rs可表示为
rs=r+λsh
(2)
式中:λs为轮刺系数,通常取0.5[12]。
为了适应车轮的形状特征,以Bekker承压模型[18]为基础,正应力可表示为轮地接触角的函数:
(3)
式中:kc、kφ、N是描述土壤承压特性的固有参数,分别为土壤内聚变形模量、摩擦变形模量和沉陷指数。轮地接触角θ1、θ2和θm是沉陷量与应力分布系数系数c1、c2和c3的函数。
(4)
θm=(c1+c2s)θ1
(5)
θ2=c3θ1
(6)
式中:s为滑转率。
通常情况下θ2较小,可将其简化为0。
为了表现车轮滑转沉陷的动态效应,沉陷指数N可表示为滑转率s的线性函数[19]
N=n0+n1s
(7)
(8)
同时,考虑车轮轮刺对于剪切应力的影响,以Janosi剪切模型[20]为基础,土壤剪切应力τ可表示为
(9)
式中:c、φ、K为土壤固有的剪切特性参数,分别表示内聚力、内摩擦角和剪切变形模量;j(θ)为土壤的剪切位移;σ(θ)为正应力。考虑轮刺效应时的剪切位移[12]可表示为
j(θ)=rs[(θ′1-θ)-(1-s)(sinθ′1-sinθ)]
(10)
(11)
(12)
式中:θ′1为考虑轮刺效应的进入角;Rj为考虑轮刺效应的等效剪切半径;sj1和sj2为过渡滑转率。一般情况下,sj1=0.15,sj2=0.5。
根据以上分析,轮地相互作用受到地面力学特性的影响,分别由法向承压特性参数组{kc,kφ,N}和切向剪切特性参数组{c,φ,K}具体表征。通过地面力学参数利用轮地相互作用模型可计算轮地相互作用力和力矩;反之亦可利用轮地相互作用力和力矩进行地面力学特性参数的估计。
2 地面力学特性参数灵敏度分析
参数的灵敏度反映了参数变化对数学模型响应的影响程度,灵敏度较大的参数对模型拥有更强的调整能力,可视为主导参数用于直接反映模型的变化情况。对轮地相互作用模型中的参数进行灵敏度分析能够确定模型的主导参数,在应用中可仅用主导参数估计结果反映相互作用力变化,以提高控制的实时性。轮地相互作用模型中含有积分公式,为非线性模型,参数间还存在较强的耦合性,用局部法分析各参数的灵敏度过程复杂且精度不高。因此,根据轮地相互作用模型的特点,采用Sobol方法对模型中的地面力学特性参数进行全局灵敏度分析。
2.1 Sobol灵敏度分析方法
Sobol灵敏度分析方法[21]是基于多重积分的分解方法,可以对非单调、非线性、非叠加等复杂模型进行分析,且允许分析各参数同时变化的情况,用于获得参数之间的耦合作用,参数的变化范围可拓展到整个参数定义域。
Sobol灵敏度分析方法假设模型中需要分析的参数个数为n,根据各参数的取值范围,定义一个n维单元体In={x|0≤xi≤1;i=1,2,…,n}作为输入参数的空间域。Sobol方法的核心思想是把平方可积函数f(x)分解为如式(13)所示的常数项、单个参数以及各参数间相互结合的函数项[22]
+f12…n(x1,x2,…,xn)
(13)
式中:f0为常数项。其他各子项对其所包含每个元素变量的积分为0,即
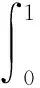
(14)
将式(13)的左右两边分别在整个参数空间域内平方并积分,结合式(14)可以得到
(15)
则函数f(x)的总方差可以表示为
(16)
(17)
根据式(17)函数总方差等于各阶方差之和,有
(18)
f(x)的各阶偏方差与其总方差的比值就是参数的各阶灵敏度,则全局灵敏度指数Si1i2…is为
(19)
同时,根据式(19)可得所有参数的灵敏度之和为1,即
(20)
在Sobol方法中,低阶灵敏度反映了单个参数对模型输出的影响,高阶灵敏度反映了参数间的耦合关系。由式(19)推导出的Si是参数xi的一阶灵敏度,表示参数xi发生变化时对函数f(x)的影响。Sij(i≠j)为二阶灵敏度,反映参数xi与xj同时变化时对输出的影响,同时考虑2个参数之间的耦合关系。
根据以上的理论分析,在实践中利用蒙特卡洛法进行数值积分代替解析积分估计输出结果的方差,当模型参数样本数足够大时,计算结果逼近解析解。因此可由以下公式进行灵敏度分析
(21)
(22)
(23)
(24)
式中:xim为求解域In空间中的采样点;l为蒙特卡洛采样数;上标(1)和(2)表示参数xim的2个l×n维求解域内的采样数组;x(~i)m表示除参数xim外的参数,即
x(~i)m=(x1m,…,x(i-1)m,x(i+1)m,…,xnm)
(25)
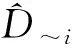
(26)
(27)
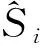
本文分析各地面力学参数对轮地相互作用力和力矩的影响,使用各参数的一阶灵敏度及其总阶灵敏度作为评价指标。
2.2 地面力学参数灵敏度分析
采用Sobol全局灵敏度分析方法,分别以轮地相互作用力和力矩为研究对象,对地面力学参数进行灵敏度分析。轮地作用模型中车轮所受土壤的宏观作用力在微观表现为正应力和切应力的组合积分,因此可分别从表征地面正应力和切应力的力学参数中筛选出主导参数,即分别对承压特性参数kc,kφ和N,剪切特性参数c,φ和K进行灵敏度比较。通常情况下,应力最大值位于进入角和离去角中间,应力分布系数c1和c2变动范围不大且受到车轮形状的影响,因此不对其做灵敏度分析,一般在研究中给定典型值。本文在试验过程中,应力分布系数的取值分别为c1=0.5,c2=0。
对地面力学参数利用Sobol方法进行灵敏度分析需要确定各参数的定义域。根据多种土壤各地面力学参数的测量值[13,16,24-25]确定取值范围,如表1所示。

表1 地面力学参数取值区间Table 1 Value range of terrain mechanical parameters
轮地相互作用模型中的其他参数设置如下:车轮宽度b=0.15 m,车轮半径r=0.14 m,等效剪切半径rs=0.145 m,滑转率s=0.3。
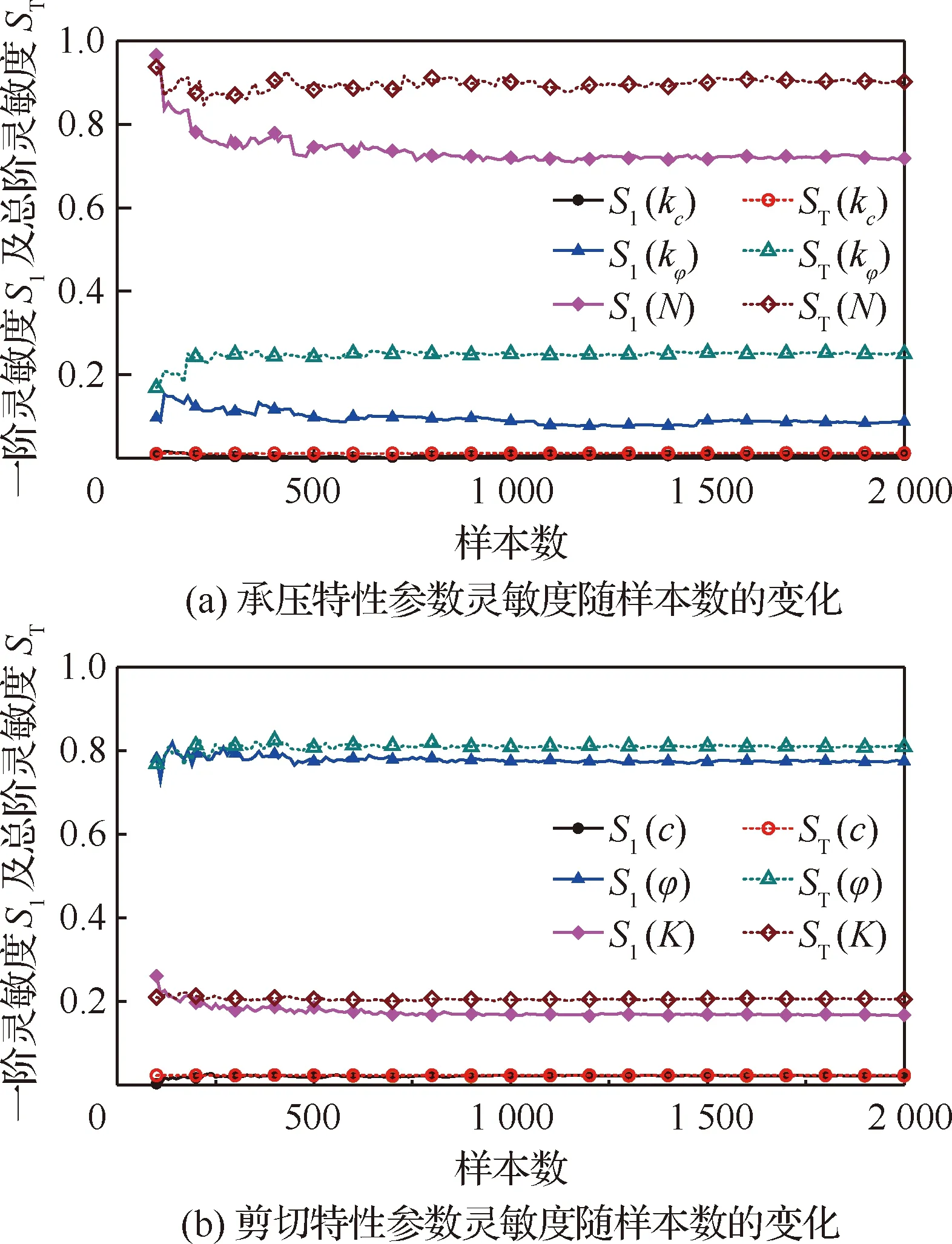
采用Sobol方法对参数进行灵敏度分析需要选择合适的采样数,采样数过少时灵敏度分析结果无法收敛,采样数过大则浪费计算资源。这里通过分析沉陷量z=0.03 m时各参数对挂钩牵引力的灵敏度随样本数的变化情况用于确定合适的采样数。对承压特性参数进行分析时,控制剪切特性参数不变,参数取值分别为c=2 kPa,φ=30°,K=0.015 m。同理,在进行剪切特性参数分析时,保持承压特性参数不变,参数取值分别为kc=5 kPa/mN-1,kφ=1 500 kPa/mN,N=1。
不同采样大小下的各地面力学参数的一阶及总阶灵敏度分析结果如图2中所示。由曲线可以看出,在样本数小于500时各参数的灵敏度存在较大的波动,样本数大于1 000后灵敏度分析结果趋于稳定。因此,在后续试验中设置样本数为1 500,可使得灵敏度分析结果收敛并得出具有代表性的结论。整体变化趋势表明样本数对参数的灵敏度影响不大。其中,沉陷指数N始终是承压特性中灵敏度最大的参数,其一阶灵敏度约为0.7,总阶灵敏度稍大,约为0.9,说明沉陷指数与其他参数存在耦合关系;在剪切特性参数中,内摩擦角灵敏度最大,一阶灵敏度和总阶灵敏度约为0.8。
地面承压模型中正应力为沉陷量的函数,剪切模型中切应力又与正应力有关,因此参数灵敏度的分析需要考虑沉陷量的影响。使车轮的沉陷量在0.01~0.06 m之间变化,利用轮地相互作用模型计算各参数的灵敏度。根据前面的分析,设置样本数量为1 500。不同沉陷量下,各地面力学参数对于车轮受到的法向力、挂钩牵引力和驱动阻力矩的总阶灵敏度如直方图3(a)~图3(c)所示。承压特性参数方面,总体上各地面承压特性参数的灵敏度受沉陷量影响较小,沉陷指数N相对于法向力FN、挂钩牵引力FDP和驱动阻力矩MR的灵敏度均大于0.8。剪切特性参数方面,在沉陷量为0.01 m时,土壤剪切变形模量K和内摩擦角φ都表现出较高的灵敏度,内摩擦角的灵敏度略大。随着沉陷量的增加,内摩擦角的灵敏度逐渐增大,土壤剪切变形模量的灵敏度相对减小,在沉陷量为0.02 m时,内摩擦角相对于各力和力矩的灵敏度约增大至剪切变形模量的2倍。
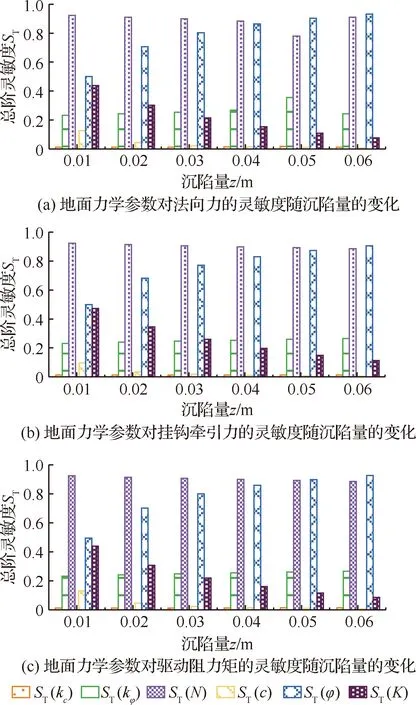
综合以上灵敏度分析结果,可以得出:① 在表征地面承压特性的参数中,沉陷指数的灵敏度最高,总阶灵敏度高于0.8,其对正应力的影响最大;② 在表征地面剪切特性的参数中,内摩擦角对于切应力的影响在总体上来说最大,同时土壤剪切变形模量在沉陷量较小时对于切应力的影响也不可忽略。因此,选择沉陷指数N和内摩擦角φ作为轮地相互作用模型的主导参数,通过估计这2个参数反映地面在承压和剪切特性方面的变化情况;其他参数(土壤内聚变形模量、土壤摩擦变形模量、土壤内聚力和土壤剪切变形模量)作为非主导参数,可根据经验赋予典型值,以提供更准确的主导参数估计结果。
3 主导参数估计
3.1 主导参数解析模型
在轮地相互作用模型中轮地作用力宏观表现为土壤应力的积分,在应力公式的原始形式下,积分难以直接求解,因此需要对应力的形式做适当的简化。参考常用的轮地相互作用模型的简化方法[25],对沿接触区域的轮地作用应力分布进行线性化处理
(28)
(29)
式中:σm为最大正应力;τm为最大切应力。
(30)
(31)
jm=rs[θ′1-θm-(1-s)(sinθ′1-sinθm)]
(32)
式中:jm为最大剪切位移。采用该线性化方法计算应力的简化误差小于15%[26]。其中最大应力角θm可表示为
(33)
该假设在滑转率较大的情况下合理成立。在大部分情况下,c1约为0.4,c2小于0.3[16]。又因为θ2约为0,θm接近θ1的一半。
利用轮地相互作用平衡方程估计主导参数,由于待辨识的主导参数仅有2个,而轮地相互作用平衡方程有3个,存在冗余,可选择其中2个方程用于主导参数求解。在实际应用中,为了减轻载荷,星球车车轮上一般不配备多维力传感器,无法直接获得车轮所受力与力矩数据。星球车的正常行驶速度较低,车轮的垂直载荷W可通过准静态分析求解得到,车轮的电机驱动力矩T可由车轮电机的输入电流估计得到,而前进阻力fDP不易直接获取或求解。因此,选择车轮垂直载荷W和电机驱动力矩T的平衡方程(式(1))用于参数求解,将简化后的正压力和切应力代入其中,经过积分与变换合并,可推导出主导参数解析表达式为
(34)
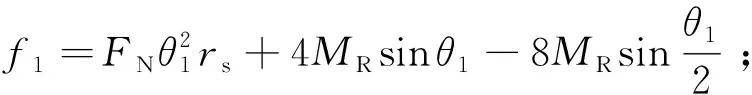
在该主导参数解析模型中,沉陷指数N的解析表达式是关于{θ1,FN,MR,kc,kφ,r,b,rs}的函数,其中{θ1,FN,MR}是系统状态参数,{kc,kφ}是非主导地面力学参数,{r,b,rs}是星球车的车轮尺寸参数;内摩擦角φ的解析表达式则是关于{s,θ1,θ′1,FN,MR,c,K,r,b,rs}的函数,其中{s,θ1,θ′1,FN,MR}是系统状态参数,{c,K}是非主导地面力学参数,{r,b,rs}是星球车的车轮尺寸参数。系统状态参数可通过直接或间接测量得到,车轮尺寸参数与车轮设计相关可视为已知参数,而非主导参数则可根据地面力学特性赋予适当的典型值,以完成对主导参数的估计。
3.2 基于解析模型的主导参数估计方法
基于提出的主导参数解析模型,固定非主导参数,可对主导参数进行估计。该方法本质上是将主导参数视为模型整体性质的外在表现,主导参数的变动情况可以直接反映土壤性质的变动,从而使星球车可以根据土壤性质的改变调整其控制和规划策略以提高其移动性能。具体估计方法如图4所示。
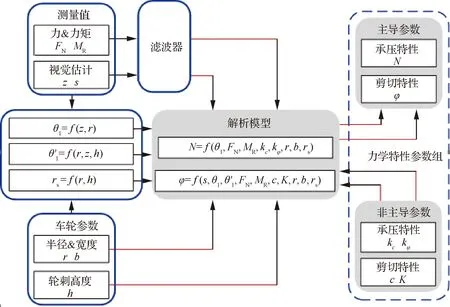
车轮所受的法向力FN和驱动阻力矩MR通过车轮垂直载荷W和电机驱动力矩T反映,且分别通过车体准静态分析和电机电流估计得到。车轮沉陷量z可通过外部视觉系统[27]或车体的位姿进行估计,滑转率s通过测量车轮转动角速度和行驶的线速度求解得到。车轮的角速度则通过车轮中安装的编码器测量,线速度可通过惯性导航原件测量[26-27]或通过视觉里程计[28]和车体运动学求解。星球车车轮尺寸参数已知,中间参数θ1,θ′1和rs可由r,z,h间接计算得到。另外,非主导地面力学参数可根据地形赋予典型估计值。
由于系统状态参数的测量值存在噪声,因此对数据进行滤波处理以减弱噪声对估计结果准确性的影响。考虑星球车不同的运行状态,当其稳定低速行驶时采用递推平均滤波方法;当车轮经过不同地形交界处时,由于地面的力学特性发生变化,对应的系统状态参数将随之剧烈变化,若变化幅度超过设定阈值,则采用中值滤波对原始数据进行处理。采用均值滤波可以抑制车体平稳运行时的数据噪声,同时起到平滑的作用;在地形变化处利用中值滤波的方法能够保护数据尖锐的边缘信号,实现数据的快速改变;均值滤波与中值滤波相比计算复杂度低,可在车体平稳运行时加快计算速度。对应伪代码如算法1所示。

算法1 主导参数估计输入:沉陷量序列Sz={z1, z2, …, zn}, 滑转率序列Ss={s1, s2, …, sn}, 法向力序列SF={FN1, FN2, …, FNn}, 驱动阻力矩序列SM={MR1, MR2, …, MRn}, 元素数量为n,非主导参数{kc, kφ, c, K},车轮尺寸参数{b, r, rs, h},滤波器宽度L,滤波器切换阈值{T1, T2, T3, T4},终止条件Ne输出:沉陷指数序列SN, 内摩擦角序列Sφ1: fori←1 tondo2: ^zi←DATAFILTER({z1, z2, …, zi}, L, T1)3: ^si←DATAFILTER({s1, s2, …, si}, L, T2)4: ^FNi←DATAFILTER({FN1, FN2, …, FNi}, L, T3)5: ^MRi←DATAFILTER({MR1, MR2, …, MRi}, L, T4)6: θ1←θ1(^zi, r)7: θ'1←θ'1(^zi, ^si, r, h)8: ^Ni←N(θ1, ^FNi, ^MRi, kc, kφ, r, b, rs)9: ^φi←φ(^si,θ1,θ'1,^FNi, ^MRi, c, K, r, b, rs)10: i←i + 111: add ^Ni to SN

12: add ^φi to Sφ13:end for14:15:Function DATAFILTER(S, L, T)16: i←number of elements in sequence S17: ai←i-th element in sequence S18: ai-1←(i-1)-th element in sequence S19: flag L20: ifi
4 试验验证
4.1 基于仿真的地面力学特性主导参数估计试验
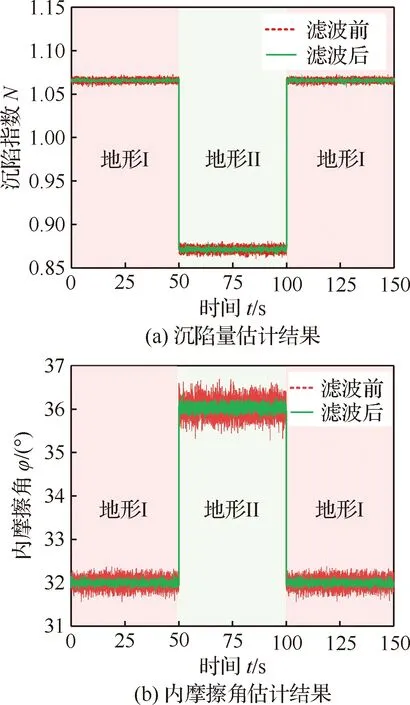
为了检验模型的准确性,通过仿真模拟轮地相互作用力和力矩进行地面力学主导参数估计试验。仿真所用车轮相关尺寸参数参考星球车原理样机的车轮[12]设置,各参数取值为:r=0.135 m,b=0.11 m,h=0.015 m。仿真模拟星球车车轮由地形I经地形II再到地形I的直线行驶过程,地形I和地形II的地面力学参数[29]如表2所示。仿真所得系统状态参数FN和MR通过添加高斯白噪声以模拟实际测量值误差,不同参数所添加的噪声标准差列于表3中。各系统状态参数的采样频率设为100 Hz。

表2 仿真地形的地面力学参数值Table 2 Mechanical parameters of terrain in simulation

表3 系统状态参数噪声标准差Table 3 Standard deviation of system state parameter noise
对仿真数据进行主导参数估计,所用滤波器的宽度L设置为11,滤波方法切换的阈值Thx为5倍白噪声的标准差。经过滤波处理和未经滤波处理的主导参数估计结果对比如图5所示。从图中可以看出,对系统状态参数测量值进行滤波可明显改善噪声对主导参数估计结果的影响,在第一种地形中沉陷指数和内摩擦角估计结果的标准差分别由1.97×10-3和0.117°减小为6.20×10-4和0.036 3°。同时,所设计的滤波方法能够快速跟随地形的变化,对地形交接处突变数据的估计结果也能保持较好的波形。对地形I,沉陷指数的平均估计误差为3.11%,内摩擦角的平均估计误差为0.03%。对于地形II,相应的误差分别是3.12%和0.11%。在同一地形中采用递推平均滤波代替中值滤波有效地降低了计算量。因此,主导参数估计方法能够快速跟随地面特性的变化,同时较大程度上抑制测量噪声,获得较为准确的估计结果。
4.2 基于单轮试验的地面力学特性估计试验
为了检验主导参数解析模型及其估计方法在真实轮地相互作用中的效果,使用哈尔滨工业大学研制的星球车单轮测试平台(如图6所示)进行不同工况下的轮地相互作用试验进行验证。使用单个星球车车轮在平坦的模拟月壤[29]中进行轮地相互作用试验,所用模拟月壤经过通风干燥、过筛和烘烤等处理,其地面力学参数已在表4中列出。所用车轮半径r为0.157 3 m,车轮宽度b为0.165 m,车轮轮周均布24个高度h为0.015 m的直型轮刺。

表4 模拟月壤的地面力学参数值Table 4 Terrain mechanical parameters of lunar simulant
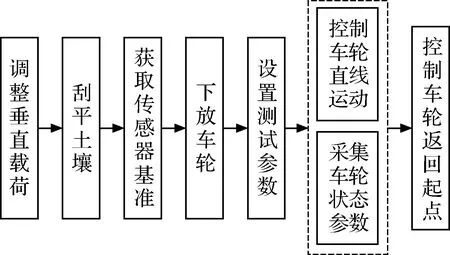
单轮测试台驱动车轮运动,车轮的实际速度由拖拽电机控制,角速度由驱动电机控制,通过改变2个电机的转速实现不同滑转率的工况。车轮上方安装有直线位移传感器用于测量车轮沉陷量。车轮与支架连接处安装有六维力传感器和扭矩传感器,能够测量车轮垂直载荷、前进阻力及电机驱动力矩。实验中,车轮轮刺的存在使得载荷波动范围较大,为了减小载荷波动带来的相对误差,将垂直载荷设定为比较有代表性的80 N。参考实际星球车的移动速度,设定车轮的线速度为0.01 m/s,为避免车轮发生过大的沉陷,设定车轮滑转率在0~0.6之间变化。驱动车轮在模拟月壤I中进行直线运动实验,在车轮达到稳定状态后采集力、力矩和沉陷量等车轮状态数据,系统的采样频率为6.67 Hz。具体试验过程如图7所示。

由于轮刺的作用,采集到的力和力矩数据存在周期性的小幅波动,根据对数据波形的分析,设置滤波器的宽度为3个波动周期,滤波器方法切换的阈值为4倍波形幅值。利用采集的数据通过主导参数解析模型对沉陷指数N和内摩擦角φ进行估计。
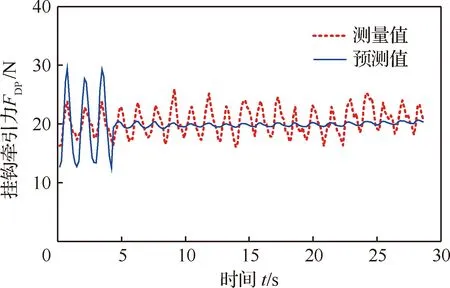
滑转率为0.4时的地面力学主导参数估计结果如图8所示。在轮刺造成波动的前3个周期内,测量得到的参数不满足滤波条件没有进行滤波,故估计结果存在较大的波动;第3个周期之后,沉陷指数和内摩擦角的估计结果分别约在1.17和32°附近小幅波动。估计得到的地面力学主导参数以及系统状态参数可代入式(1)中预测车轮受到的挂钩牵引力,预测值与实际测量值如图9所示。测量值在17~25 N间波动,预测值约在20 N附近,表明利用求解得到的地面力学主导参数能够较准确地预测地面给车轮的牵引力。
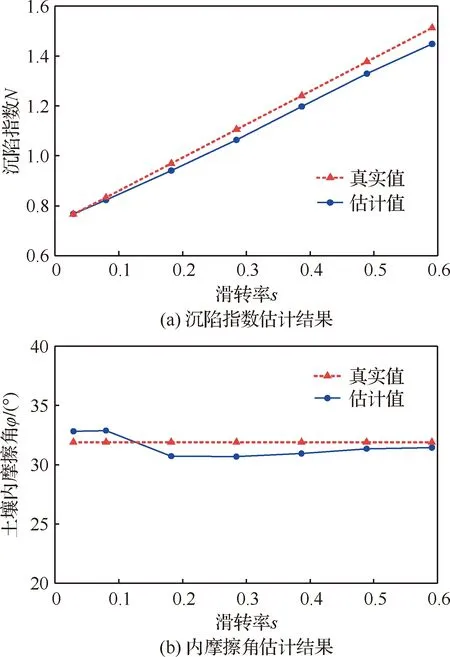
4.3 滑转率对估计结果的影响
此外,本文还利用不同滑转率下车轮在模拟月壤II中的轮地相互作用实验检验了该估计方法的滑转率适用范围。车轮滑转率在0~0.6之间的地面力学特性主导参数估计结果如图10所示。从图中可以得出,沉陷指数与滑转率呈线性关系,这也说明了将沉陷指数表示为N=n0+n1s的形式的合理性。沉陷指数预测值与真实值的误差非常小,不同滑转率下的平均相对误差为2.8%。内摩擦角在滑转率0~0.6之间的估计值与真实值偏差较小,平均相对误差为2.8%。
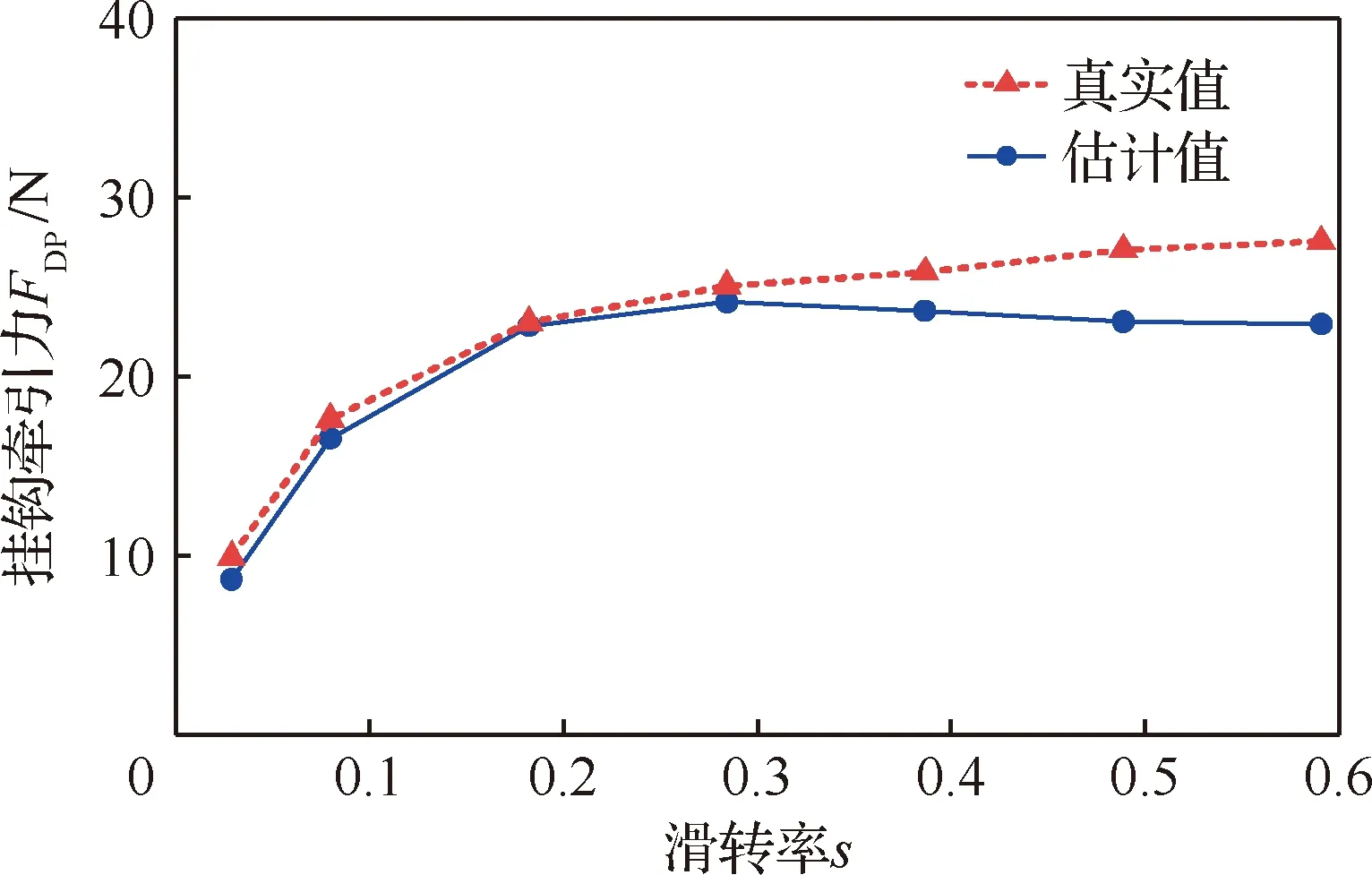
利用主导参数的估计值预测车轮的挂钩牵引力(图11),在滑转率小于0.3时,预测值与测量值相差较小,随着滑转率增大,两者之间的偏差逐渐增大,平均满量程误差为7.4%。在主导参数估计和挂钩牵引力预测过程中,测量值与预测值之间较大的偏差主要由固化轮地接触角系数c1,c2和c3的参数值引起,在仅以有限主导参数拟合模型的情况下,对挂钩牵引力7.4%的平均满量程误差结果在可接受范围内。
4.4 非主导参数对估计结果的影响
在验证试验中,为了说明主导参数解析模型的效果,采用了准确的地面力学特性非主导参数值用于估计。而在实际应用中,非主导参数通常基于经验赋予标称值,该标称值可能与真实值之间存在偏差,因此需要分析非主导参数的变动对于估计结果的影响。
根据前文地面承压特性参数和剪切特性参数的灵敏度分析结果,得出灵敏度仅次于沉陷指数N和内摩擦角φ的参数分别为土壤摩擦变形模量kφ和土壤剪切变形模量K,而土壤内聚变形模量kc和土壤内聚力c的灵敏度都接近于0,其对于主导参数求解结果的影响可以忽略。为了验证估计方法对于非主导参数变化的鲁棒性,变换不同的kφ和K进行估计试验。同时为了说明车轮沉陷量的影响,控制沉陷量在0.01~0.06 m内改变,估计结果如图12所示。

由图12可知,土壤摩擦变形模量kφ的减小,会使沉陷量指数N的估计值降低,并且所选用的kφ典型值与真实值偏差越大,对应的沉陷指数估计值降低得越快,当所选用的kφ典型值的与真实值的偏差在500 kPa/mN范围内时,N的估计误差小于0.1。同时,随着沉陷量的增加,kφ变动对于N的影响稍有增加。对于内摩擦角,随着土壤剪切变形模量K的增大,φ的估计值也会相应地增大,沉陷量为0.01 m时,K的值在0.003 m内变化,φ的偏差小于4°;另外,随着沉陷量的增加,内摩擦角的估计结果受到土壤剪切变形模量的影响越小,K的影响就相应减弱。当沉陷量z=0.06 m 时,K的值增加一倍,其对于φ的影响小于6°。从总体来说,土壤摩擦变形模量kφ和土壤剪切变形模量K对于主导参数估计结果的影响较小,并且当取适当的典型值时,估计结果可以保证有较高的精度。
5 结 论
1) 在表征地面承压特性的参数中,沉陷指数N的总阶灵敏度高于0.8,在地面承压特性参数中灵敏度最高,对轮地作用力和力矩的影响最大;内摩擦角对于轮地作用力和力矩的影响在地面剪切特性参数中最大。因此,沉陷指数N和内摩擦角φ可作为主导参数用于反映地面承压和剪切特性的变化。
2) 所推导的地面力学主导参数的解析模型以轮地相互作用力和力矩为输入,以地面力学特性主导参数为输出,在已知车轮尺寸参数的情况下,以标称值固定非主导参数的方式,可用于地面力学特性主导参数估计。
3) 所提出的主导参数估计方法通过对系统状态参数进行滤波以抑制测量噪声能够快速跟随地形的变化。在不同滑转率下,主导参数估计结果总体上表现出较小的误差,沉陷指数估计值较真实值的平均相对误差为2.8%,内摩擦角的平均相对误差小于3%,且估计结果对非主导参数的变化具有鲁棒效果。本文的估计方法对精确的全参数估计和基于轮地相互作用的控制均具有参考价值。
