基于GNSS多径信号的反射面参数估计算法

邵乙伦，赵娟，刘承禹，王岩，陈新

(1.上海交通大学 电子信息与电气工程学院，上海 200240；2.96901部队25分队，北京 100094)

0 引言

无人机、智能车等移动载体利用各式传感器收集环境反射信号来感知周边环境.该环境信息可应用于场景感知、避障、路径规划和定位增强等领域[1-2].在全球卫星导航系统（GNSS）多径反射信号利用方面，全球卫星导航系统反射（GNSS-R）技术是一种新型的微波遥感技术.该类技术的核心是通过观测目标GNSS反射信号特征参数来估算目标参数，如测算海面高度、海面风场、土壤湿度等[3-4].然而上述研究无法直接应用于接收机周边环境感知及导航定位.在城市峡谷环境下，GNSS信号被城市建筑等障碍物阻挡并产生大量多径信号.目前，该类多径信号主要被归类为有害干扰信号并被GNSS接收机加以抑制或剔除[5-7].若能有效利用多径信号中的空间环境信息，则可以在不增加额外开销的情况下提高接收机的环境感知能力.

针对上述问题，本文提出了一种基于GNSS多径信号的反射面参数估计算法.在GNSS多径信号感知和特征参数提取方面，码相位延迟幅度联合跟踪算法（CADLL）对接收机跟踪环路的时域相关峰进行检测，在多径信号存在时利用标准参考波形对发生畸变的时域相关峰进行扣减，将多径信号成分从时域相关峰中剥离[8].该算法在抑制多径误差的同时能够实现多径信号特征参数的提取.在分析了GNSS多径信号结构及其几何传播过程后，给出了多径信号传播模型.由于相关模型含有大量的非线性运算，本文选用粒子滤波算法作为反射面定位算法.粒子滤波算法是一类贝叶斯估计方法，该算法利用蒙特卡洛法对复杂的统计积分公式进行数值估计，能够对非线性及非高斯噪声系统参数进行估计[9-10].GNSS真实信号实验结果表明，本文所提算法能够有效估计GNSS多径信号反射面位置参数.

1 系统模型

1.1 GNSS多径信号特征参数

城市峡谷等复杂场景下，GNSS信号经一次或多次反射到达接收机天线，产生多径效应.接收机接收到卫星直达径（LOS）信号和多径信号.根据GNSS信号结构，接收到的GNSS信号s(t)可表示为

式中：i=0表示LOS信号；A为LOS信号的幅值；D(t)为导航电文；αi为多径信号相对LOS信号的衰减系数；C(t−τi)为扩频码；τi为多径码相位延迟；f0为载波频率；fdi为载波多普勒频率；φi为多径信号相对LOS信号的相位变化.易知α0=1，τ0=0，φ0=0.多径信号特征参数，即多径衰减系数αi、码相位延迟 τi、多普勒频率fdi和相位偏移 φi，唯一确定了GNSS多径信号.

1.2 GNSS多径信号传播模型

根据卫星、接收机、反射面间的几何关系，建立GNSS多径信号传播模型.该模型假设多径信号经反射面单次反射后到达接收机天线.以接收机初始时刻位置为原点建立东、北、天（E、N、U）地理坐标系.下文所述的位置、速度参数均使用该地理坐标系表示.传播模型的几何关系如图1所示.卫星位置为psat，卫星速度为vsat，反射面镜像卫星位置pmirsat，镜像卫星速度为vmirsat，接收机位置为precv，接收机速度为vrecv，反射面法向量为np，反射面距离为d，反射面方位角φazi定义为反射面法向量在地理坐标系水平面内的投影向量与N方向间的夹角（北偏东为正），反射面俯仰角θele定义为反射面法向量与法向量水平面投影间的夹角（法向量指向天向时为正）.反射面法向量、反射面距离、反射面方位角、俯仰角、距离唯一确定了反射面位置参数.

图1 GNSS多径信号传播模型几何关系

反射面法向量可以由反射面方位角、俯仰角表示：

反射面解析方程表达式如下：

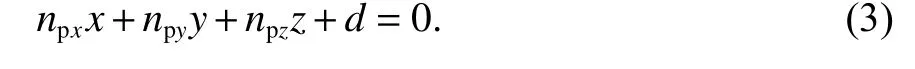
镜像卫星的位置速度参数可以利用反射面解析方程计算得出，也可以采用类似于姿态求解过程中等效旋转矢量的思路来求解[11].基于等效旋转矢量方法，公式（4）、（5）给出了镜像卫星位置速度求解公式.

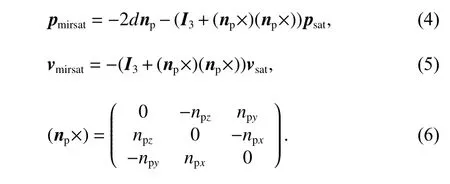
式中：I3为三维单位向量，(np×)为反射面法向量的反对称矩阵.

由于多径反射信号的幅值与反射面的介质相关，因此很难建立幅值与反射面位置参数的数学模型.本文主要对多径码相位延迟τ和多普勒频率漂移fdfading进行建模分析.

多径信号的码相位延迟 τ是由LOS信号和多径信号的传播路径长度差异造成，因此可以利用式（7）建立模型.

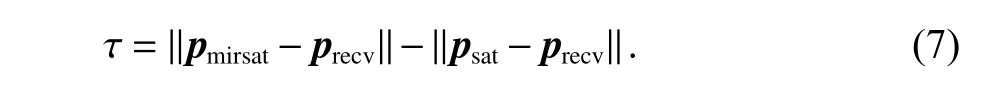
式中，“ ∥∥”为向量取模运算.

多径多普勒频率漂移fdfading反映了多径信号多普勒频率相对于LOS信号多普勒频率的偏移，与卫星和接收机的运动有关，可以建模为式（8）.

式中：λ为载波波长；“·”为向量点积运算.

2 粒子滤波多径反射面参数估计

在接收机跟踪环路，CADLL算法实现了GNSS多径信号的感知和特征参数提取，为反射面参数估计提供了多径码相位延迟 τ和多普勒频率漂移fdfading原始观测量.接收机PVT解算模块提供的接收机、卫星的位置、速度信息为GNSS多径信号传播模型提供参数信息.由传播模型可以看出，反射面位置参数与多径信号观测量之间存在大量的非线性运算，常规的卡尔曼滤波已无法满足此类非线性观测需求.因此，本文采用适用于非线性系统的粒子滤波算法来估计反射面位置参数信息，计算过程分为以下几个步骤：

1)初始化

由于算法中所讨论的GNSS多径信号反射面主要指城市建筑外墙，因此反射面俯仰角初始化值的取值范围限制在[−10,10]°；反射面方位角初始化值的取值范围是[φazisat−90,φazisat+90]°，其中 φazisat为卫星方位角；反射面距离初始化值的取值范围是 [0,τ0]m，其中 τ0为初始多径码相位延迟.

2)系统状态更新

本文假设反射面为单一平面且保持静止，因此粒子更新方程如下式所示：

3)计算多径观测量预测值

根据每个粒子的方位角、俯仰角、距离值及接收机、卫星的位置、速度信息，利用多径信号传播模型中式（7）、（8）计算预测多径码延迟和预测多普勒频率漂移

4)粒子权重更新及归一化

本文假设多径观测量服从独立的二维高斯分布，则粒子权重更新过程如下式所示：

式中：σ1表示码延迟观测噪声标准差；σ2表示多普勒频率漂移观测噪声标准差.

若粒子俯仰角不满足[−10,10]°取值范围或粒子方位角不满足式（13）所示的取值范围，

式中，θelesat为卫星俯仰角，则认为该粒子值不满足镜面反射几何关系并将该粒子的权重归零.

粒子权重归一化过程如下式所示：

5)粒子重采样

根据更新后的粒子权重对粒子进行重采样操作，防止粒子退化.根据更新后的粒子权重值，计算权值累积分布函数（CDF），如下式所示：

6)计算反射面位置参数估计值

7)计算多径信号反射点位置

多径信号反射点坐标(prpx,prpy,prpz)可通过求解如下方程组得到：

式中：t为辅助参数；(precvx,precvy,precvz)为接收机位置坐标；nmp为镜像卫星单位视线矢量，坐标为(nmpx,nmpy,nmpz)，计算公式如下：

3 实验结果与分析

本文分两次实验对算法进行测试.两次实验分别是上海交通大学微电子楼天台的标定实验以及上海市陆家嘴市区环境实验.实验使用GNSS中频采样设备对GNSS原始信号采样得到中频原始数据，利用实验室包含CADLL算法的软件接收机对中频原始数据进行基带信号处理和PVT解算得到多径信号观测数据及定位解算导航信息.将观测数据代入粒子滤波反射面参数估计程序，计算得出反射面参数估计结果，其中反射面估计频率为10Hz.

GNSS信号中频采样过程中尽量增加采样带宽以提高多径特征参数提取精度，本文GNSS信号采样带宽为32MHz.

3.1 微电子楼天台标定实验

上海交通大学微电子楼天台北侧和西侧天空被建筑外墙遮挡，另外两侧天空则是开阔的.接收机天线置于天台地面，方位角接近90°的低仰角卫星信号经西侧建筑外墙反射产生多径信号，GNSS天线同时接收LOS信号和多径信号.微电子楼天台标定实验中，GNSS信号及接收机参数如表1所示.

表1 天台标定实验GNSS信号及接收机参数

使用高精度实时动态（RTK）接收机测量墙面标定点坐标，通过解析几何计算可以得到地理坐标系下的反射面参数标定值.相对接收机位置处的地理坐标系，天台实验的标定结果为反射面方位角φazicali=69.8°，俯仰角θelecali=0°，距离dcali=19.6m.将多径观测数据代入粒子滤波反射面估计程序，反射面估计结果如图2所示.

图2 天台标定实验反射面参数估计结果

根据反射面参数估计结果和反射面参数标定值，评估反射面估计效果.反射面估计的绝对值误差如图3所示.

图3 天台标定实验反射面参数估计绝对值误差

计算反射面估计的均方根误差（RMSE），计算公式如式（23）所示，计算结果如表2所示.

式中：y为反射面参数估计值；ycali为反射面参数标定值；N为实验数据长度.

表2 天台标定实验反射面位置估计RMSE

从实验结果可以看出，反射面位置参数估计结果收敛于标定值，估计RMSE较小，算法实现了对微电子楼天台西侧建筑外墙反射面位置参数的估计.

3.2 陆家嘴市区环境实验

在陆家嘴市区环境进行数据采集并进行粒子滤波反射面参数估计，GNSS信号及接收机参数如表3所示，反射面参数估计结果如图4所示.对反射点位置坐标求平均值得到反射点位置估计，如图5所示.

表3 陆家嘴市区环境GNSS信号及接收机参数

图4 陆家嘴市区环境实验反射面参数估计结果

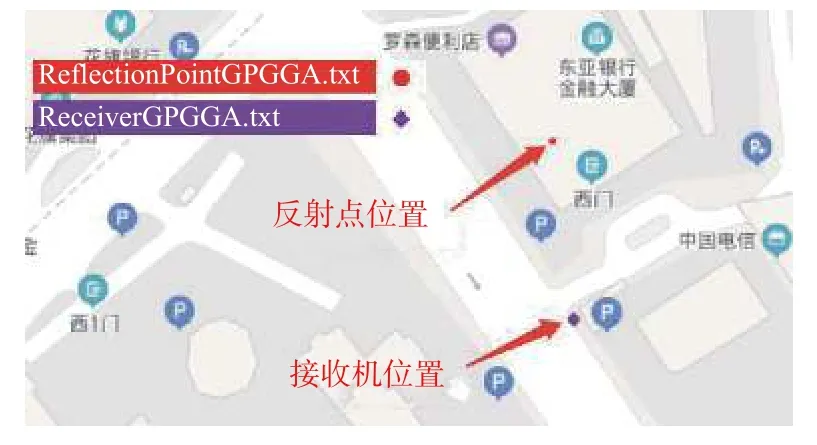
图5 陆家嘴市区环境实验反射点位置估计结果

图6为粒子滤波反射面参数估计算法多径码相位延迟原始观测值.由图6可知，码相位延迟值小于80m.根据GNSS多径反射信号传播几何关系，该多径信号的反射面距离小于80m.由卫星方位角为173.9°可知，反射面方位角的取值范围为 [83.9,263.9]°.利用百度地图接收机所在位置处的全景地图，满足上述方位角和距离要求的反射面仅有如图5所示的东亚银行金融大厦.算法实现了市区环境GNSS多径信号反射面感知与参数估计.

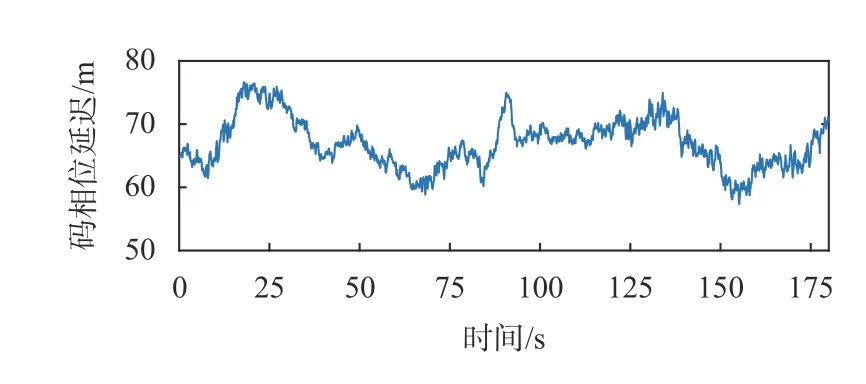
图6 陆家嘴市区环境实验多径码相位延迟观测值

由反射面估计结果可知反射面方位角在175°左右.由于本文反射面法向量定义为由反射面指向地理坐标系坐标原点，而卫星方位角或百度全景地图朝向的法向量定义为地理坐标系中由接收机指向目标，因此实验估计的反射面在百度地图全景功能中的朝向为355°.图7为利用百度全景地图得到的多径反射场景示意图，其中反射点所在建筑为东亚银行金融大厦.

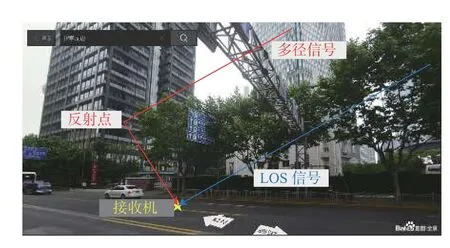
图7 陆家嘴市区环境实验多径反射场景

4 结束语

本文对城市峡谷环境下GNSS信号中的LOS信号和多径信号的传播模型进行建模分析，基于粒子滤波算法实现了多径反射面的位置参数估计.该算法具有较高精度.静态环境下，反射面方位角RMSE小于10°，俯仰角RMSE小于5°，距离估计RMSE小于10m.在不增加传感器的情况下，本文所提算法提高了接收机的周边环境感知能力，相关感知信息可应用于场景感知、避障、路径规划和定位增强等领域.