基于PCA-SMO的CSI指纹定位方法

孟俊剑，邹进贵，赵胤植

(1.武汉大学 测绘学院，武汉 430079；2.桂林理工大学 广西空间信息与测绘重点实验室，广西 桂林 541006)

0 引言

随着移动互联网技术及物联网等的不断发展，使得基于位置的服务(LBS)在人们生活中的重要性日益突出[1-4].在室外可以通过目前比较成熟的全球卫星导航系统(GNSS)技术获得亚米级的精度，然而在室内环境中，由于建筑物的遮挡现象比较严重，使得可利用的GNSS信号难以满足室内定位的需求.在室内定位领域的众多解决方案中，由于W i-Fi设备的普及率较高，W i-Fi信号广泛存在于各种室内空间，使得W i-Fi信号成为一种比较理想的定位源[5-6].

传统的基于W i-Fi接收信号强度指示(RSSI)的定位方法操作简单，但由于RSSI易受多径、时变等因素的影响[7]，基于RSSI的定位方法定位精度难以有效提升.随着IEEE 802.11n系列无线局域网通讯协议中应用了多输入多输出(M IMO)和正交频分复用(OFDM)等技术，使得收发端设备之间的信道特征即信道状态信息(CSI)可以在物理层进行估计[8].CSI揭示了散射、衰落及功率随距离衰减等综合效应，是无线信号在空间传播更为本质的描述，其为提升定位精度及改善多径效应等问题提供了新途径[9-10].

现有的基于CSI的室内定位方法大致可以分为指纹匹配、测角和测距三类[11]，其中基于指纹匹配的定位方法由于受多径效应影响较小、易于实施等优点而备受关注.相比于RSSI，CSI中包含更为丰富的特征信息，可以构建更高维的指纹库[12-14]，但同时也导致构建的指纹库存储量大、构建定位模型所需的计算和时间开销大及实时定位计算量大等问题[15].对此本文提出首先使用主成分分析(PCA)的方法对原始指纹信息进行降维得到主要特征，而后利用序列最小最优化(SMO)算法构建指纹点主要特征与其位置的回归模型并用于位置预测.

1 CSI指纹定位方法

基于指纹的定位方法通常分为离线阶段和在线阶段.在离线阶段，首先将定位区域划分为若干格网，而后分别在各个格网处利用终端采集来自各个接入点的无线信号，然后提取无线信号的特征构建指纹库；在线阶段利用同样的方式得到待定点的指纹特征，将其与指纹库中记录逐条比对来确定待定点的位置.

1.1 CSI的获取

CSI反映了无线通信链路的信道属性，相比于MAC层的RSSI，物理层的CSI是一种更细粒度的信息.对于OFDM系统的窄带平坦衰落信道，其信道模型可以表示为

式中：Y和X分别表示接收向量及发送向量；H为信道矩阵；N为高斯白噪声.信道矩阵H可通过下式进行估计：

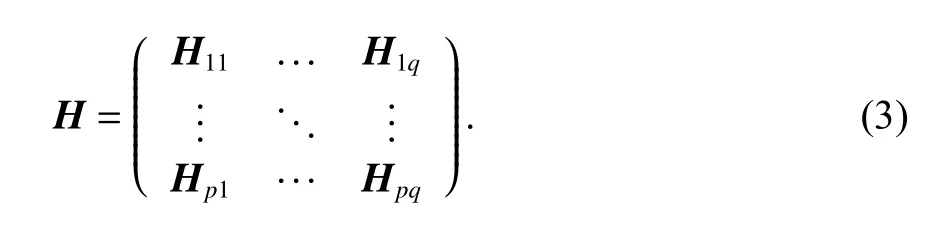
式中：p和q分别为发射和接收天线的个数；Hpq表示第p根发射天线和第q根接收天线组成的通信链路对应的信道矩阵，并且有

式中：n为OFDM系统中子载波个数；Hpq,i为链路Hpq第i个子载波对应的CSI信息，其可以表示为

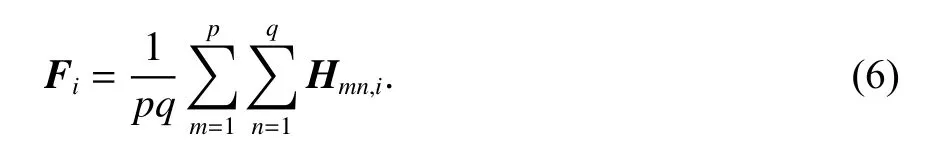
1.2 CSI指纹数据预处理

使用CSI采集工具得到的原始CSI信息为形如a+bi型的复数值，幅值 |H|和相位 ∠H可按下式计算：

在数据采集过程中，由于硬件设备的不稳定及人员走动等因素的影响使得采集的信号中难免会有一些异常值，因此有必要对其进行过滤和剔除.本文采用拉依达准则（3σ准则）剔除CSI幅值和相位数据中的异常值，而后通过均值滤波的方法得到该点的指纹特征.

1.2.1 CSI幅值预处理

按式(7)可计算出CSI的幅值，图1给出了在同一位置采集的200个数据包的对应原始幅值，可以发现同一子载波的振幅大都集中在某一范围内，但也存在少许偏差较大的异常值，图2给出了利用3σ准则对异常值剔除之后的幅值，可以发现原始幅值中的异常值可被有效的剔除.

图1 同一位置200个数据包的原始幅值

图2 剔除异常值之后的幅值

1.2.2 CSI相位预处理

与CSI幅值不同，利用式(8)计算得到的相位值不能直接利用，这是由于硬件设备的限制，使得发射端和接收端的同步误差不能完全消除，使得接收端接收到的CSI中包含由时钟同步误差引起的采样频率偏移以及由不同载频误差引起的载波频率偏移.这也使得CSI相位信息在室内定位中的应用受到限制，目前常用的一种做法是采用线性变换的方法对原始相位进行校正[16-17]，但由于测量得到的原始相位是缠绕相位，如图3所示需要先对其进行解缠，然后对解缠后的相位进行校正.图3是在同一位置处采集的200个数据包对应的原始相位，解缠后的相位如图4所示.

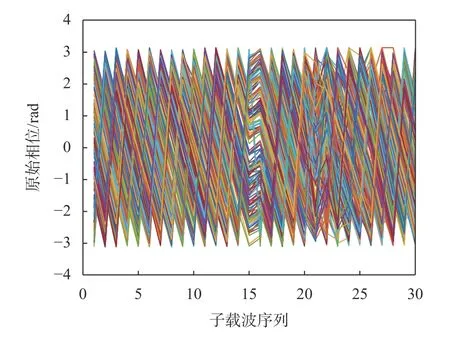
图3 同一位置200个数据包的原始相位

图4 解缠后相位

线性变换的方法如下：设第i个子载波解缠后的相位为，则有

式中：φ为第i个子载波的真实相位；mi为第i个子载波的编号；N为快速傅里叶变换的大小，在802.11 a/g/n协议中N为64；∆t为由采样频率偏移导致的时间偏差；β为由载波频率偏移引起的相位偏移；Z为测量噪声.由于∆t和β均为未知量，故难以直接计算真实相位，但可以通过的线性变换消除这两个未知量，这里引入两个中间量k、l，其中：

图5给出了经线性变换后的相位，图6给出了使用3σ准则剔除异常值后的相位.

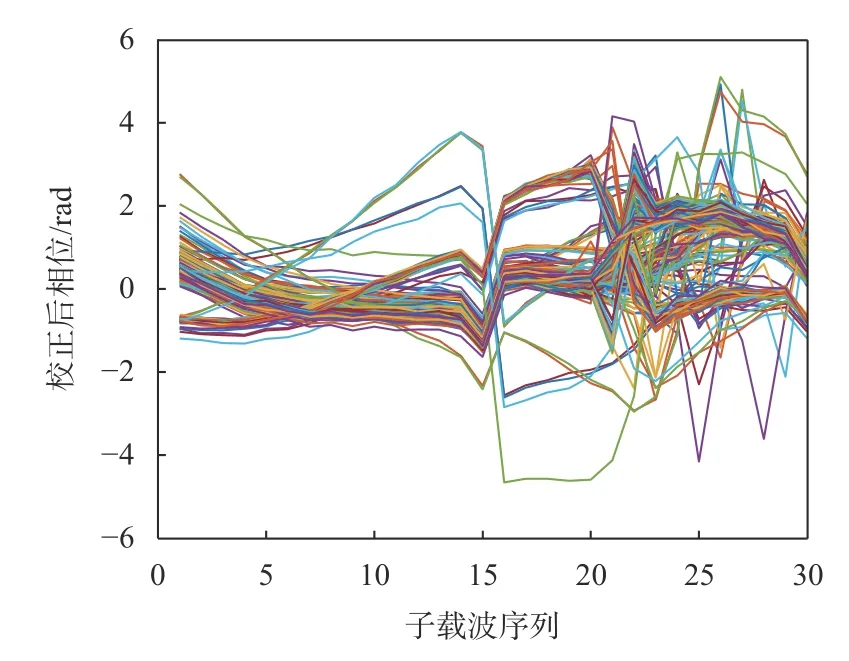
图5 线性变换后相位

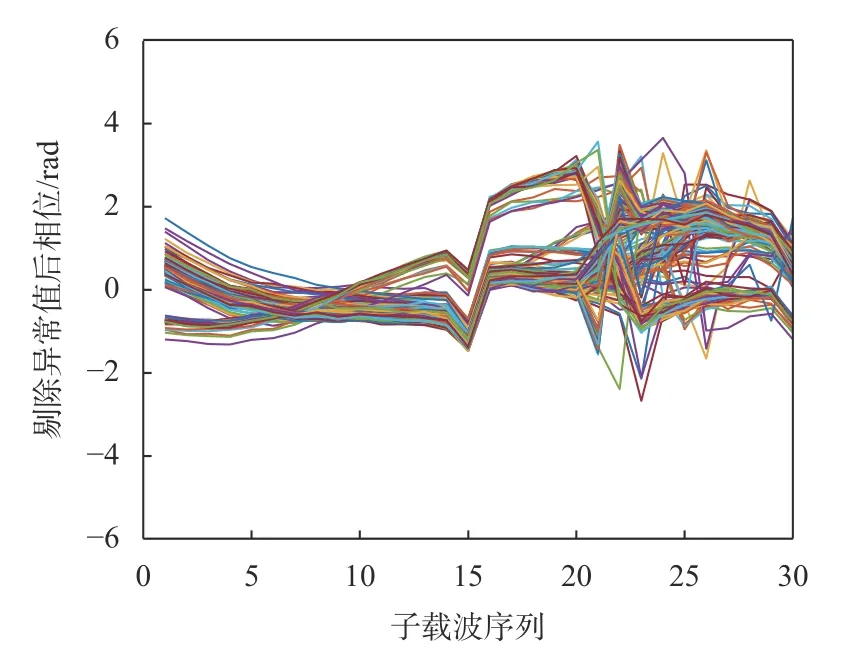
图6 剔除异常值后相位

2 PCA-SMO定位算法

本文使用的算法首先在离线阶段提取出指纹点CSI的幅值和相位特征构建原始指纹库 (Fi,Li)，i=1,2,···,n，其中，Fi=(fi1,fi2,···,fit)为原始指纹特征，t为原始指纹特征维数，Li=(xi,yi)为对应指纹点的坐标，n为指纹点的个数；而后对原始指纹库进行PCA降维提取出主要特征，得到降维后的指纹库其中，m为降维后的特征维数；然后利用SMO算法建立指纹点的主要特征与其位置的支持向量回归(SVR)模型：并利用此关系模型对测试点的位置进行预测.

2.1 PCA变换

PCA作为一种重要的数据降维方法，已被广泛应用于数据分析、图像处理及机器学习等领域，用以减少数据冗余及数据去相关等[18].其核心思想是将原始数据通过线性变换投影到一个新的数据空间（即主成分空间），通过选取对原始数据方差贡献最大的若干维主成分来实现数据的降维.本文利用PCA对原始CSI指纹特征进行降维基于这样一种假设：由一对收发天线组成的通信链路上的各子载波信号从发射端到接收端的传播路径是趋于一致的，即受到多径等因素的影响相当，故这组子载波的信号特征存在一定的相关性，可以通过降维减少数据冗余.原始数据与保留的主成分之间的转换可以通过一个投影矩阵来实现，表1给出了PCA变换的伪代码.

表1 PCA变换伪代码

2.2 SMO算法

SMO算法是由Platt在1998年提出的用于训练支持向量机(SVM)的一种快速算法[18].本文旨在利用SMO算法建立降维后的指纹点特征与对应位置坐标的SVR模型

进一步可得SVR的解的表达式：

式中，σ为高斯核函数的带宽.

SVM的分类及回归问题均可化为求解凸二次规划的问题，此类问题具有整体最优解，但在训练样本数量较大时，计算开销正比于样本量且实现较复杂，SMO算法的出现很好地解决了这一问题.SMO算法是一种启发式算法，其基本思路是每次循环选出两个需要更新的变量 αi,αj，并固定其余参数，利用解析的方法对式(16)快速求解并更新 αi,αj，循环将原问题分解为子问题并对子问题进行求解，最终达到求解原问题的目的.本文采用开源的机器学习及数据挖掘软件Weka中提供的SMO回归算法包构建回归模型，选用的高斯核参数σ=0.015，本文算法的整体框架图如图7所示.

3 实验与分析

3.1 实验环境

实验地点在武汉大学测绘学院114实验室(7.0m×6.5m)，实验室摆有桌椅等杂物.实验选取大小为4.8m×4.8m的方形区域，布设41个指纹点，如图8实心点所示，图中格网边长为0.6m，另外随机选取30个测试点用于算法的精度评估.实验使用一台不设密码型号为TL-WDR5620的双发双收四天线路由器，接收终端为一台装有Intel 5300无线网卡（三个接收天线）的笔记本，CSI采集工具为安装在Ubuntu 14.04操作系统上的linux-80211n-csitool开源工具包[19].数据采集过程中路由器放于地面，采集者首先操作笔记本连接路由器，然后依次站在设定的位置利用ping命令进行数据包的采集.同时为模拟真实环境，实验过程中保持实验区域有人员走动，每个指纹点和测试点均采集250个数据包.数据采集完成后，利用文献[19]中提供的linux-80211n-csitool-supplementary工具包对各个点位的原始.dat文件进行解析，得到原始的CSI信息.

图8 实验区域指纹点布设示意图

3.2 实验结果分析

根据实验配置，离线阶段构建的原始指纹特征维数为60，通过PCA变换选择保留原始指纹95%的主成分信息，得到新指纹特征的维数为4.经过PCA变换之后的指纹库存储量约为原始指纹库的1/15.显然，在建立降维后的特征与对应坐标的回归模型时所需的计算开销及时间成本也将大大减少，这一点对于以手机为代表的计算资源有限的移动定位终端来说具有重要意义.

经过PCA变换，原始指纹信息不可避免的存在一定程度的损失.文章首先探究了先进行PCA变换再通过SMO算法建立降维后指纹特征与对应位置的回归模型以及直接利用SMO算法建立原始指纹特征与对应位置的回归模型两种方式对定位精度的影响，图9给出了在分别利用25、50、100、150、200及250个数据包对测试点进行定位时PCA-SMO与SMO算法的平均定位误差.

图9 PCA-SMO与SMO算法平均定位误差对比

从图中可以看出，SMO算法的定位精度整体上均优于PCA-SMO算法，但随着定位所利用的数据包数量逐渐增多，两者定位误差的差距逐渐缩小，最终稳定在5 cm之内.总的来看，在综合考量离线阶段建模的计算及时间开销、定位的实时性等因素时，PCA变换带来的精度损失是可接受的，尤其是在以手机端为代表的消费级室内定位应用场景中，因此进行PCA变换是有必要的.

此外，本文还在相同实验条件下对比了PCA-SMO算法与邻近算法（KNN）、WKNN、FIFS[20]及CSI-M IMO[21]等算法的定位效果.图10给出了上述几种定位算法的定位误差累积分布函数.

图10 定位误差累计分布函数

由图10可得：本文算法整体是最优的且可靠性要高于其它几种算法；当定位误差小于等于1.5 m时，本文算法的累计概率为70%，而KNN、WKNN、FIFS及CSI-M IMO算法的累计概率分别为53%、35%、57%、43%；PCA-SMO算法在2m之内定位误差的累计概率可以达到97%，其它几种算法的累计概率依次为80%、70%、77%、87%.

最后，表2统计了上述几种算法的定位误差.其中本文PCA-SMO算法的平均定位误差为1.25m，其它几种定位算法的平均定位误差分别为1.52m、1.60m、1.56m、1.57m，相比于其它几种算法，本文算法的平均定位精度分别提升了21.6%、28.0%、24.8%、25.6%.

表2 几种定位算法的定位误差统计 m

4 结束语

W i-Fi作为室内定位领域的重要定位源之一，传统的基于RSSI的指纹定位方法由于可利用的特征信息有限，导致其定位精度受到限制.而CSI中包含丰富的特征信息，可以在一定程度上改善由于指纹特征不足带来的精度问题，但与此同时，离线阶段构建的指纹库存储量变大、构建定位模型的计算和时间开销以及定位的实时性等问题也应受到关注.对此，本文提出的PCA-SMO算法首先对原始指纹特征进行PCA降维，然后通过SMO算法构建降维后指纹与对应位置的回归模型，能够在保证定位精度的前提下，较好地克服上述问题.另外，在实时定位过程中由于人员流动等因素的影响，会使得CSI特征发生变化，寻找一种有效的异常值探测算法有待进一步研究.