基于卡尔曼滤波和改进DBSCAN聚类组合的GPS定位算法

葛倩，侯守明，赵文涛

(河南理工大学计算机科学与技术学院，河南焦作 454003)

0 引言

随着科技的不断进步，定位和导航技术不断成熟，以手机为移动终端的定位系统在经济建设、改善民生、社会生活等方面都得到普遍应用，例如:危险品运输车定位追踪[1]；无人机配送[2]；智能旅游等[3].尤其在智能旅游增强现实（AR）实景定位导航中，实时获取高精度地理位置信息处于至关重要的位置.用户通过AR实景定位导航系统获取实时坐标信息，并为游客规划清晰的旅游线路，省时、省心、省力的AR实景导航系统成为游客出行必不可少的工具.

目前，GPS系统是当前全球应用最为广泛的导航和定位系统，通过用户接收的检测卫星发送信号，从而对用户所在位置坐标进行准确定位.但由于GPS定位系统受信号传播误差、卫星特性误差和用户接收机内在误差等因素的影响，导致GPS系统定位精度低.为了提高GPS定位精度，近年，研究人员主要采用以下两种技术方法进行研究.第一种研究通过借助辅助设备：任超等[4]将移动定位技术（GPSOne）应用于智能手机定位系统，对其准确性和鲁棒性进行研究分析；Zandbergen等[5]对比了辅助GPS（A-GPS）、W iFi和蜂窝定位技术，在此基础上提高了高灵敏度GPS手机定位精准度[6].第二种研究利用智能手机自带芯片的设计算法来提高定位的精准度：杜晓辉等[7]分别将最小二乘法和卡尔曼滤波应用于静态单点定位，并比较了二者的定位误差，证明卡尔曼滤波算法可以有效地利用噪声统计特征对坐标量进行估计，得到较好的定位精度；刘志忠等[8]使用卡尔曼滤波算法消除了GPS数据中较大的数据波动,并通过模糊C-均值聚类算法确定数据中心，验证了此方法提高GPS定位的合理性；刘胜等[9]提出了一种基于模糊C-均值聚类算法和卡尔曼滤波算法的组合优化方法，首先通过卡尔曼滤波算法对GPS数据去噪，然后使用模糊C-均值聚类分析，聚类中心点为最终定位坐标，降低了定位成本，提高了GPS单点定位的精准度；崔少星[10]则首先采用DBSCAB密度聚类算法去除偏离度较大的数据点，然后对所剩的数据进行算术均值运算，即获得GPS精确定位的坐标数据信息；袁阳等[11]针对手机GPS定位系统采集的数据信息分别进行动态卡尔曼滤波和静态卡尔曼滤波设计，实验验证了卡尔曼滤波算法对处理手机GPS原始数据定位的可行性，其中，动态低速卡尔曼滤波算法定位结果最好.

基于上述对GPS单点定位算法的研究，虽然有效控制了GPS定位误差范围，但定位精度还需提高.因此，本文提出使用卡尔曼滤波结合改进的DBSCAN聚类思想提高GPS定位精度.首先通过卡尔曼滤波去噪缩小误差范围，然后提出一种基于DBSCAN二次聚类加权重心的GPS定位误差修正策略，进行二次去噪和聚类定位，并将此算法应用于AR实景定位导航系统中，以低成本提高GPS定位的精准度，且有较好的鲁棒性.

1 卡尔曼滤波模型及数据处理

卡尔曼滤波算法通过系统输入、输出的观测数据计算线性系统状态方程，将系统状态进行最优估计.由于受各种因素的影响，GPS采集到的数据存在很大波动，采用卡尔曼滤波算法能有效去除观测数据中的噪声和干扰信号，获得可靠的定位信息.

卡尔曼滤波模型由线性系统状态的预测方程和观测方程两部分组成：式（1）、式（2）中：A为状态转移系数矩阵；xk和xk−1分别为k、k−1时刻的系统状态变量；Wk−1为k−1时刻的过程激励噪声；Zk为观测变量；H为测量系数矩阵；Vk为对应经纬度上的高斯白噪声.卡尔曼滤波过程如下：

1）通过k−1时刻预测k时刻的状态

2）通过k−1时刻估算k时刻的系统误差Pk

式中，Q为观测噪声协方差矩阵。

3）更新卡尔曼增益Kk

式中，R为测量噪声协方差矩阵.

4）由预测值、观测值和更新后的卡尔曼增益，获得k时刻最优估计

5）在系统运行结束前，卡尔曼滤波需要计算当前时刻的系统误差，以便下一时刻进行计算.k时刻的系统误差Pk

式中，I为单位矩阵.

我们将手机GPS系统采集到的数据，采用卡尔曼滤波算法处理分析.图1（a）为原始GPS数据分布图，图1（b）为采用卡尔曼滤波后的GPS数据分布图.由实验分析可知，经过卡尔曼滤波去噪，有效消除数据中较大的数据波动，经纬度平均误差被控制在5.2 m，但获取更加精准的真实位置坐标点仍需进一步的数据处理.

图1 卡尔曼滤波后的GPS数据分布

2 DBSCAN聚类加权重心定位模型

DBSCAN作为基本的聚类分析算法，研究的目的是尽可能形成密度可达的数据点最大簇，能快速进行聚类且对噪声数据的区分，簇的形状可任意构成[12].采用改进的DBSCAN聚类思想对GPS采集的数据集进行二次聚类和二次去噪，并通过密度聚类分析，获取更精确的位置坐标.

2.1 DBSCAN算法的相关定义

1）邻域（Eps）：以对象p为核心，Eps为半径的圆，即

式中：Nε(p)为以p为核心以Eps为半径的圆内数据对象；D为样本数据；dist(p,q)为对象p、q两者间的距离.

2）数据阈值（M inPts）：在Eps邻域内，所有数据对象的数量最小阈值即为数据阈值MinPts.

3）核心数据对象：对象p的Eps邻域内的样本数大于或等于MinPts时，对象p即为核心数据对象.

4）直接密度可达：q在核心数据对象p的ε邻域内，即为对象q是从对象p的直接密度可达.

5）密度可达：在样本数据集D中，若存在一串数据对象p,p1,p2,···,pn,q，并且对象p1是从对象p直接密度可达，对象pi+1是从对象pi直接密度可达，即对象q是从对象p密度可达.

6）密度相连:在样本数据集D中,所有对象都是密度可达时，即称为互为密度相连.

7）簇和噪声：与核心数据对象p密度可达的所有对象即成为一个簇，不被包含在簇内的点，即称为噪声点.

2.2 DBSCAN原理

DBSCAN算法主要思想是将邻域内密度相连的数据点的最大数据集归类合并成一个簇，进而将所有各组密度相连的样本划为不同的类别.算法描述如下：

1）通过扫描整个数据集D，随机选择一个未分类的数据对象p；

2）根据对象数量Nε(p)和数据阈值MinPts进行判断：若Nε(p)≥MinPts，则p为核心数据对象，并且找到从该核心数据对象p出发的Eps邻域内所有密度相连的数据对象，构成一个簇；否则将p标记为噪声；

3）重复步骤2），直到将数据集D中的所有数据遍历完,即数据对象被归为某一簇或者认定为噪声，结束运行.

2.3 DBSCAN算法改进

为了进一步提高GPS定位精准度，我们对DBSCAN聚类思想提出改进.首先将分类后的数据进行二次聚类，将误判为噪声的点归入最近的簇内，然后在类中求算术均值和类间加权求重心，图2是算法流程图，算法步骤如下：

图2 改进DBSCAN算法流程图

1）输入终止迭代条件φ以及最大迭代次数Maxtimes；

2）计算各簇中心

通过计算各个噪声到簇中心点的距离，将误判为噪声的点归入最近的簇内，并重新计算该簇的中心点；

3）当迭代条件满足|E1−E2|<φ或者迭代次数为Maxtimes，结束算法，否则继续迭代.

4）将经过二次聚类的分类结果，求类中算术均值，即

5）类间加权求重心，即(Gx,Gy)

式中：H为数据集过滤后的数据总和；为加权之后的重心，即为最终GPS定位系统坐标.

3 实验结果与分析

GPS定位系统的精度容易受到环境因素影响，因此，本文以视野空旷的城市中心P1和偏僻的山谷P2为例，采用手机内置的GPS集成设备，对固定地点每隔5 s输出一次定位数据，将连续获取的200个数据组成原始数据集进行算法测试.

同时，考虑到AR实景导航系统APP对移动终端设备高性价比的需求，本文采用中低端移动平台华为畅享10手机作为算法测试平台，该终端性能参数如表1所示.

表1 华为畅享10手机参数

详细实验步骤及结果分析如下：

1）采用卡尔曼滤波处理GPS采集到的经纬度坐标数据.图3（a）为P1经过卡尔曼滤波后的数据分布，经纬度平均误差为4.7m；图3（b）为P2经过卡尔曼滤波后的数据集分布，经纬度平均误差为7.8m.

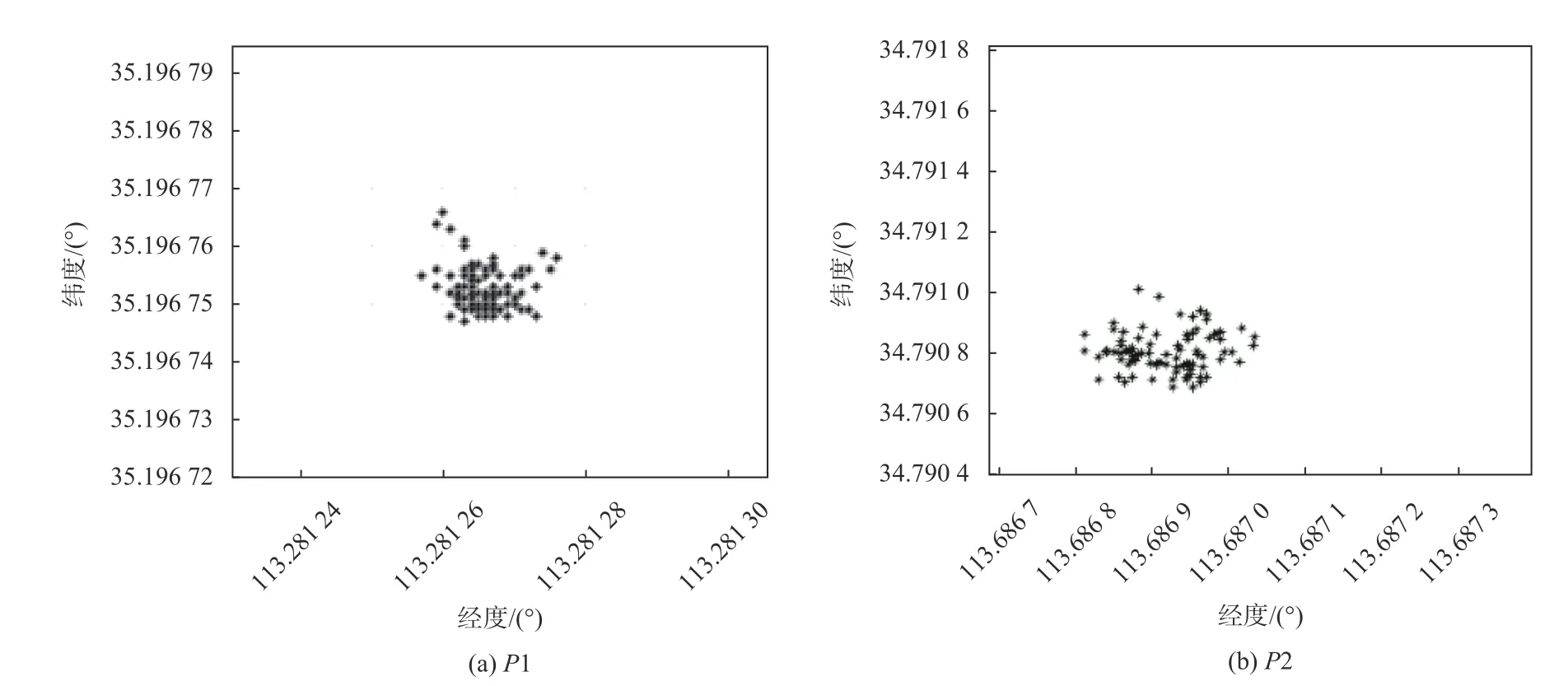
图3 卡尔曼滤波后的数据分布

2）使用改进后的DBSACN聚类思想对卡尔曼滤波后的GPS数据进行分析.由于GPS定位数据坐标的误差只有万分位以后的数据有变化，为了使实验结果更加明显，我们直接对变化的数据位数进行实验分析.

由于不同的Eps和MinPts的参数值直接影响聚-类结果，本文采用李文杰等[14]提出了基于K-平均最临近数据关联与DBSCAN相结合的K-ANN-DBSCAN算法获取参数，该算法根据数据集自身分布特点，自动选取最优参数值，并得到高准确度的聚类结果.实验结果显示，P1点：Eps=1.1，MinPts=3；P2点：Eps=28，MinPts=5是最优参数组合.

图4（a）和图4（b）分别为P1聚类前后的数据分布.图5（a）和图5（b）分别为P2聚类前后的数据分布.其中黑色为噪声点，不同颜色为不同的簇.

实验结果表明，P1和P2的数据被分为3簇，误差较大的点被准确的标记为噪声，误判为噪声点的数据经过二次聚类归为相应的簇内，聚类效果理想.

图4 P1聚类前后数据分布

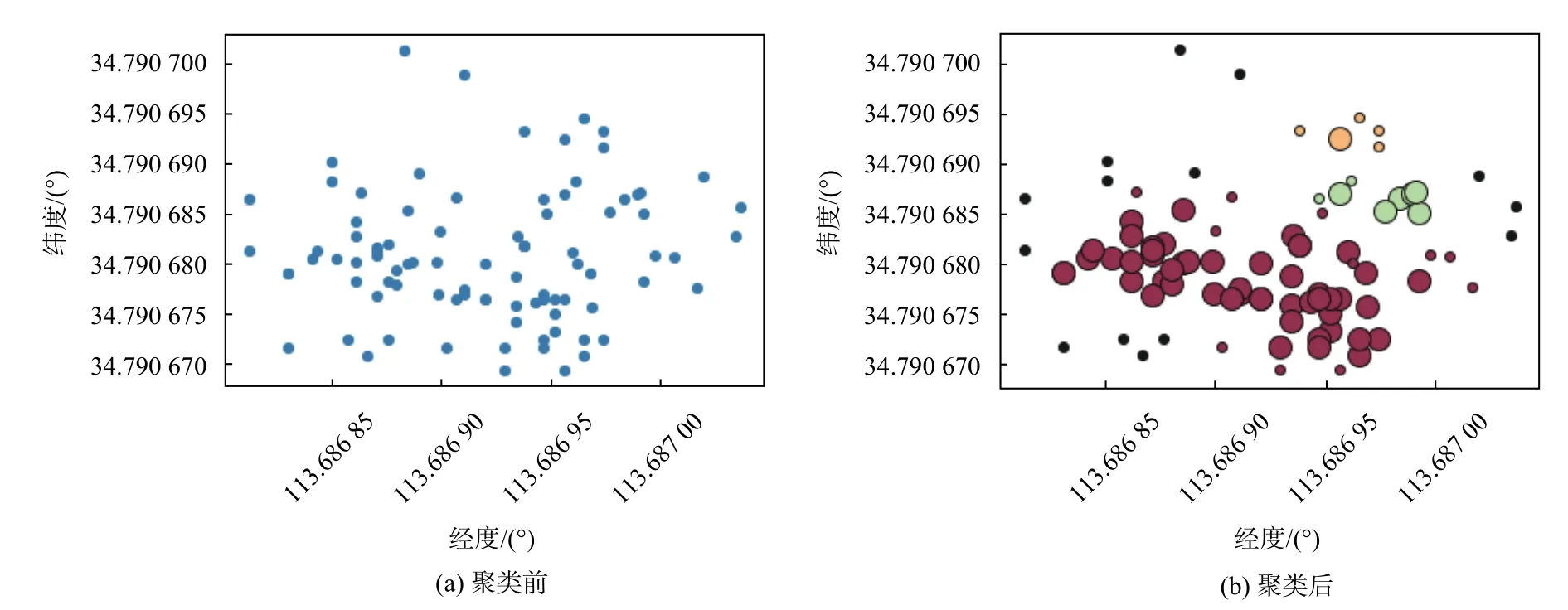
图5 P2聚类前后的数据分布

3）我们对聚类实验结果类中数据求均值，类间进行加权求重心.图6（a）和图6（b）分别为P1、P2加权求重心的聚类结果.其中三角形表示各簇中心点，五角星表示加权求得的重心，即GPS定位最终坐标点.

表2是本文算法计算得到的经纬度坐标值与真实坐标位置的误差分析.经过计算可得P1坐标平均误差是2.1m；P2坐标平均误差是3.4m.本文提出的算法经计算接近真实坐标，符合GPS系统定位误差3～5m的要求.

图6 P1、P2加权求重心的聚类结果

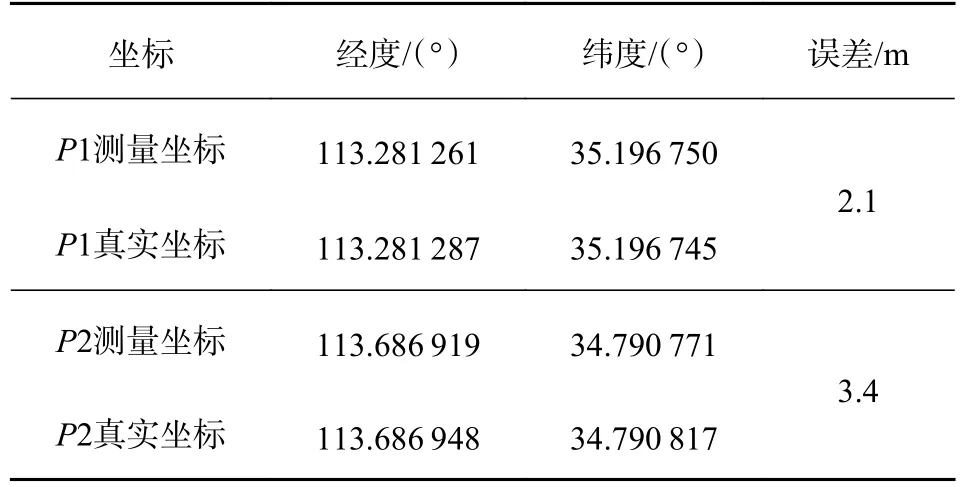
表2 P1和P2定位误差的比较

4）为了验证改进后DBSCAN算法的可靠性和准确性，我们以学校图书馆广场为例进行GPS数据采集，并与DBSCAN+算术均值算法[10]和扩展卡尔曼滤波算法[11]进行对比分析.表3是文献[10]和文献[11]的算法和本文算法在不同方向和维度的定位误差的比较分析结果.在文献[11]算法中我们主要针对低速动态卡尔曼滤波算法与本文算法的对比分析.

表3 不同算法定位精度数据对比

实验证明，本文算法与文献[10]算法相比较,在东向、北向定位精度分别提高10.72%和9.79%，在2D和3D不同维度分别提高9.81%和10.31%；与文献[11]算法相比较,在东向、北向定位精度分别提高6.40%和6.02%，在2D和3D不同维度分别提高6.36%和8.74%.本文算法有效控制了误差范围，进一步提高了GPS的定位精度.

图7～9分别是通过文献[10]、文献[11]算法和本文算法优化处理后的GPS数据分布.由图可知，本文算法相较文献[10]、文献[11]算法噪声点数量明显减少，数据误差控制在更小的范围内且集中向真实坐标点靠近.

另外，我们将此算法应用于开发的AR校园实景定位导航系统，通过在校园选择多地点进行测试，总体定位误差在3～5m，路径规划时间不足0.1 s，系统的流畅性完全满足AR实景导航系统的要求.如图10是不同方向AR实景导航路径效果图，图10（a）是西南方向，图10（b）是北方向；其中图的上部分是卫星导航地图，下部分显示实景地图.

图7 文献[10]算法定位实验结果

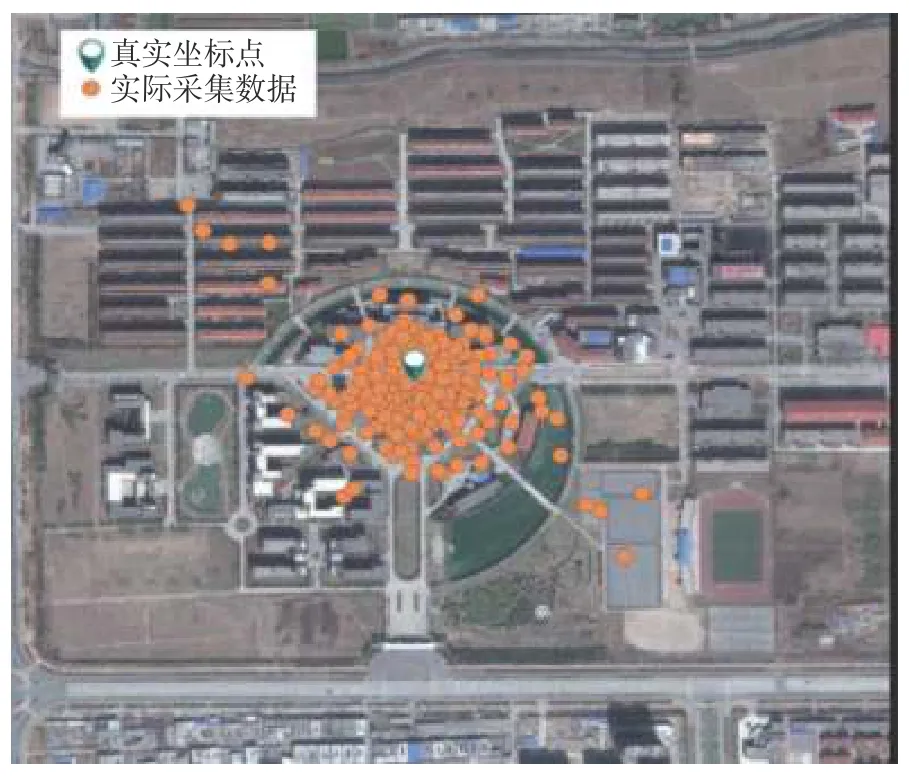
图8 文献[11]算法定位实验结果

图10 AR实景导航不同方向效果展示

4 结语

本文提出的使用基于卡尔曼滤波算法能有效控制误差范围，通过DBSCAN二次聚类加权重心修正GPS的单点定位误差的组合定位优化算法，与文献[10]和文献[11]的GPS定位算法相比，综合定位精度进一步得到提高，平均提高10.16%和6.88%左右，定位精度进一步得到提高。

基于智能手机自带GPS系统通过本文提出改进算法来提高定位的精准度，具有成本低，使用方便的优势，能够满足移动端AR实景导航系统定位精度、实时性和鲁棒性的需求.

本文未考虑复杂恶劣环境下GPS单点定位精度准确性和可靠性的问题.最近的研究表明，通过5G移动通信、多定位系统的组合[15]可以有效改善此问题.例如，彭勇等[16]提出对卡尔曼滤波算法做出改进设计，并将其应用于组合系统导航定位，提高了定位导航系统的精确度和稳定性；Zhao等[17]通过对北斗卫星导航系统（BDS）/GPS/低地球轨道（LEO）组合仿真，并在恶劣环境下进行模拟测试证明，多定位系统组合比单一定位系统的性能和定位精有所提高，但实现相对复杂；高晓等[18]将GPS/BDS组合系统应用于无人机中，改善无人机动态定位精度和可靠性.

由此，如何将本文算法进一步拓展应用于BDS/GPS/LEO组合系统导航定位，提高在复杂环境下的AR实景导航系统的定位精度将是我们下一步的研究工作.