基于PSO-LSSVM 的复杂试验不确定度分析

2021-03-25洪谭亮丁晓红王海华王神龙徐世鹏

上海理工大学学报 2021年1期

洪谭亮, 丁晓红, 王海华, 王神龙, 徐世鹏

（1.上海理工大学机械工程学院，上海 200093；2.延锋安道拓座椅有限公司，上海 201315）

测量不确定度用于表征合理赋予被测量的值的分散性[1]。目前常用的不确度评定方法是由《测量不确定度指南》（Guide to the Expression of Uncertainty in Measurement，GUM）[2]给出的A 类和B 类评定。但是当测量系统比较复杂且样本量少的时候，GUM 法评定不确定度效果不是很好。因此，2008 年8 个国际权威组织联合发表不确定度补充文件[3]，用蒙特卡罗法传递分布，补充了GUM法。计量学界广泛运用蒙特卡罗方法，崔孝海等[4]采用蒙特卡罗方法对微波功率进行了不确定度分析；孟令川等[5]通过蒙特卡罗方法与GUM 法对圆柱螺纹塞规中径的测量结果进行不确定度评定，证明了蒙特卡罗方法有更优的评估结果；朱大业等[6]采用蒙特卡罗方法对汽车座椅的鞭打试验得分进行不确定度分析，取得了很好的评价结果。陈怀艳等[7]通过小功率校准因子说明了蒙特卡罗不确定度评定方法的可靠性。

蒙特卡罗模型评定不确定度时需要根据输入量的概率密度函数产生的样本量计算出输出量，因此建立输入输出模型的精度至关重要。针对复杂试验输入与输出关系的复杂建模，目前通常采用回归监督机器学习的算法[8]： BP（ back propagation）神经网络、支持向量机（support vector machine, SVM）、迭代决策树（gradient boosting decision tree，GBRT）等回归算法。最小二乘支持向量机、BP 神经网络等算法可用于小样本、高维特征变量模型。BP 神经网络没有给定目标函数的任何假设，可以实现输入到输出的映射功能，但是对数据的要求高，对模型的训练也非常有挑战性[9]；而最小二乘支持向量机适合小数量样本，避免过学习问题，泛化能力强[10]。

本文采用具有训练样本少、预测精度高的最小二乘支持向量机算法，利用PSO 算法优化LSSVM的惩罚系数及核函数参数，解决最小二乘支持向量机在建模过程中惩罚系数及核函数参数难以确定的问题。以汽车座椅安全带拉伸试验为对象，采用PSO-LSSVM 对安全带拉伸试验建模，考虑安全带拉伸试验主要影响因素的概率密度函数，对其进行拉丁超立方试验设计，最后通过蒙特卡罗方法实现对安全带拉伸试验的不确定度分析，并以GUM 法对安全带拉伸试验的不确定度分析作为参考。

1 安全带拉伸试验不确定度影响因素

1.1 安全带拉伸试验简介

安全带是汽车发生碰撞过程中保护乘驾人员安全的基本装置，试验按照GB14167—2013 程序设置，座椅通过拉力F1和F2分别对上、下人体模块施加载荷，如图1 所示。对于M1 和N1 车型，对上下人体模块沿车辆纵向中心平面与水平方向成向上10±5 °的方向施加试验载荷，其中上人体模块施加13 500±200 N 的试验载荷，下人体模块施加相对座椅质量20 倍的载荷。试验过程中在4 s内加载到国标规定值并至少持续0.2 s，且安全带固定点不能失效，并且不能超过对应的参考面。

图1 安全带拉伸试验设置Fig.1 Safety belt tensile test setup

1.2 主要影响因素及其概率密度分布函数

安全带拉伸试验是最为复杂的汽车座椅静态试验，试验设置参数有很多，主要跟假臀和假胸的位置参数有关。根据试验标准和经验，安全带拉伸试验的主要影响因素有：假胸中心点与调角器中心点的竖直距离A、假胸倾斜的角度J、假胸与调角器的水平距离B、正视图中假胸中心线到安全带插口的水平距离O，如图2 所示。

根据工程师经验和一般统计规律可以得出A为韦布尔分布，J，B和O均为正态分布。

以某型号汽车座椅安全带拉伸试验为例，以B和O的尺寸上下极限值作为其各自概率密度分布95%置信区间的上下限，由概率统计区间估计可得出B，J，O的正态分布参数。正态分布函数记作N(μ,σ2)，其中： μ决定了其位置； σ决定了分布的幅度。同时对A设置韦布尔分布参数。韦布尔分布函数记作W(λ,k)，其中：λ为比例参数；k为形状参数。A，B，J，O的分布函数参数如表1所示。

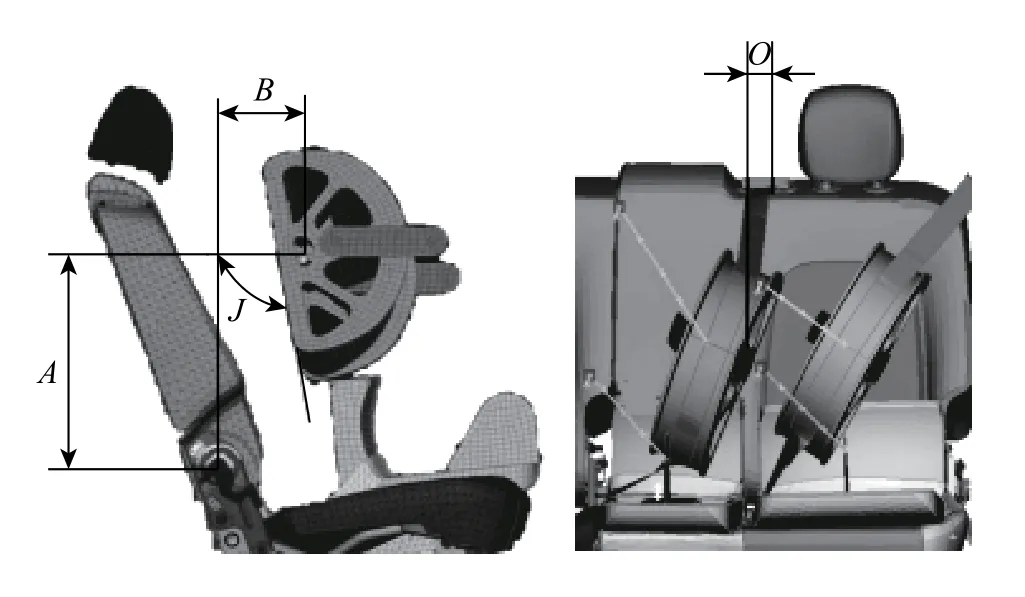
图2 安全带拉伸试验主要影响因素Fig.2 Main influencing factors of safety belt tensile test

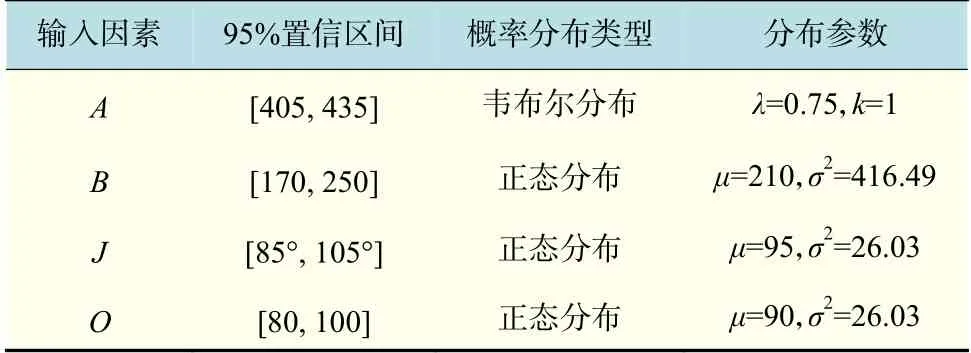
表1 A，B，J，O 的分布函数参数Tab.1 Distribution function parameters of A，B，J，O

2 安全带拉伸试验设计及仿真

2.1 有限元模型

考虑到安全带拉伸试验的成本和一些不可控因素的影响，汽车座椅安全带拉伸试验有限元模型的建立是本文进行不确定度分析的基础。依据GB14167—2013 规定的试验方法，结合某车型利用ANSA 软件对汽车座椅进行有限元建模。安全带拉伸试验有限元模型如图3 所示。

2.2 影响因素的试验设计

为了建立安全带拉伸试验输出和输入参数之间的数学模型，需要在不同输入参数下进行多组安全带拉伸试验，以便有足够的数据来建模[11]。当试验次数为固定值时，拉丁超立方采样设计非常适用。拉丁超立方采样设计对每个因子的水平数没有限制，适用于响应呈现非线性情况。抽样步骤如下：

步骤1选定设计变量，并初始化各个变量的分布区间，其各个输入参数概率密度函数如表1所示。

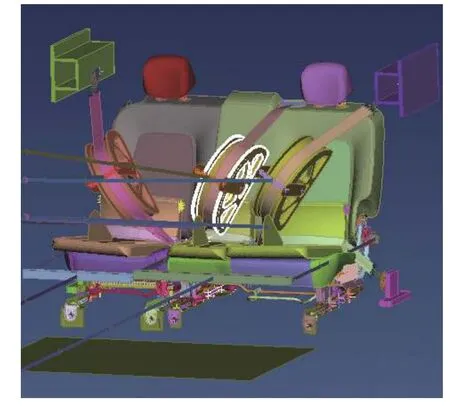
图3 安全带拉伸试验有限元模型Fig.3 Finite element model of safety belt tensile test

步骤2确定抽样次数l，考虑到设计变量的个数和试验成本，设定样本数为30。因为采取了拉丁超立方的方法抽样，30 组样本能准确地反映输入概率分布中值的分布，具有足够的代表性，得到的抽样样本具有足够的建模精度。增加样本数并不能对模型的精度有很高的提升，同时会增加训练样本的时间。将每个变量xD=(A,J,B,O)按其分布函数将纵坐标轴分成l个等分，每一等分宽度是1/l。为第D个变量的第L次抽样值，如图4所示。

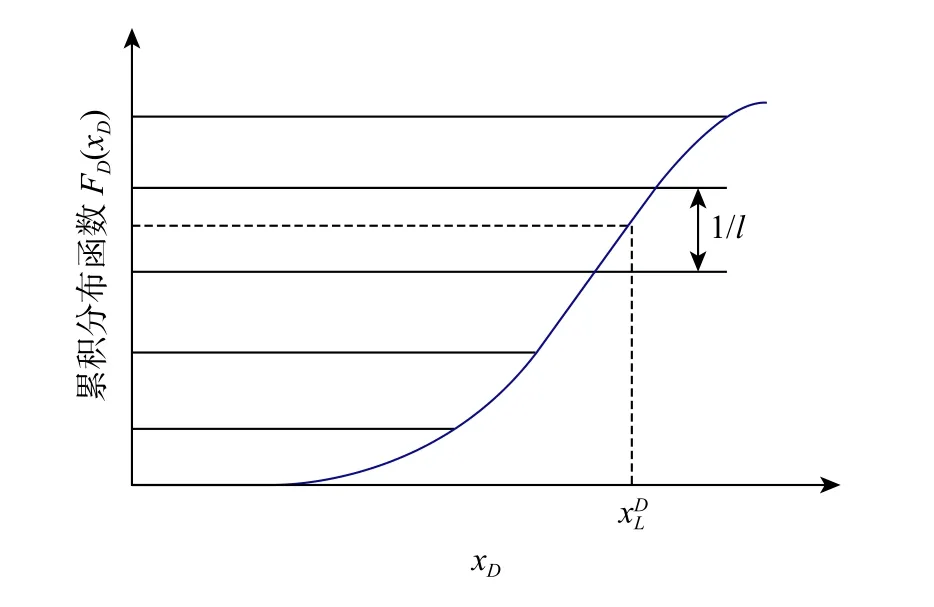
图4 考虑概率密度分布的拉丁超立方抽样Fig.4 Latin hypercube sampling considering probability density distribution

步骤3产生一个30×4 的矩阵，其每一行都是（1，l）整数随机序列，是该矩阵的第L行D列元素。

步骤4产生一个30×4 的矩阵，其每个元素均服从[0,1]均匀分布，是该矩阵的第L行D列元素。

步骤5通过计算得到30×4 的采样矩阵，为其L行D列元素。则

式中：L=1, 2, ···,l;D=1,2,···,d。

步骤6显示拉丁超立方抽样的30 组数据，如表2 所示。结合汽车座椅安全带拉伸试验有限元模型，根据试验号调整有限元模型中影响因素A，B，J，O的尺寸，可以得到安全带固定点X方向的位移BUCKLE_X，如表2 所示。

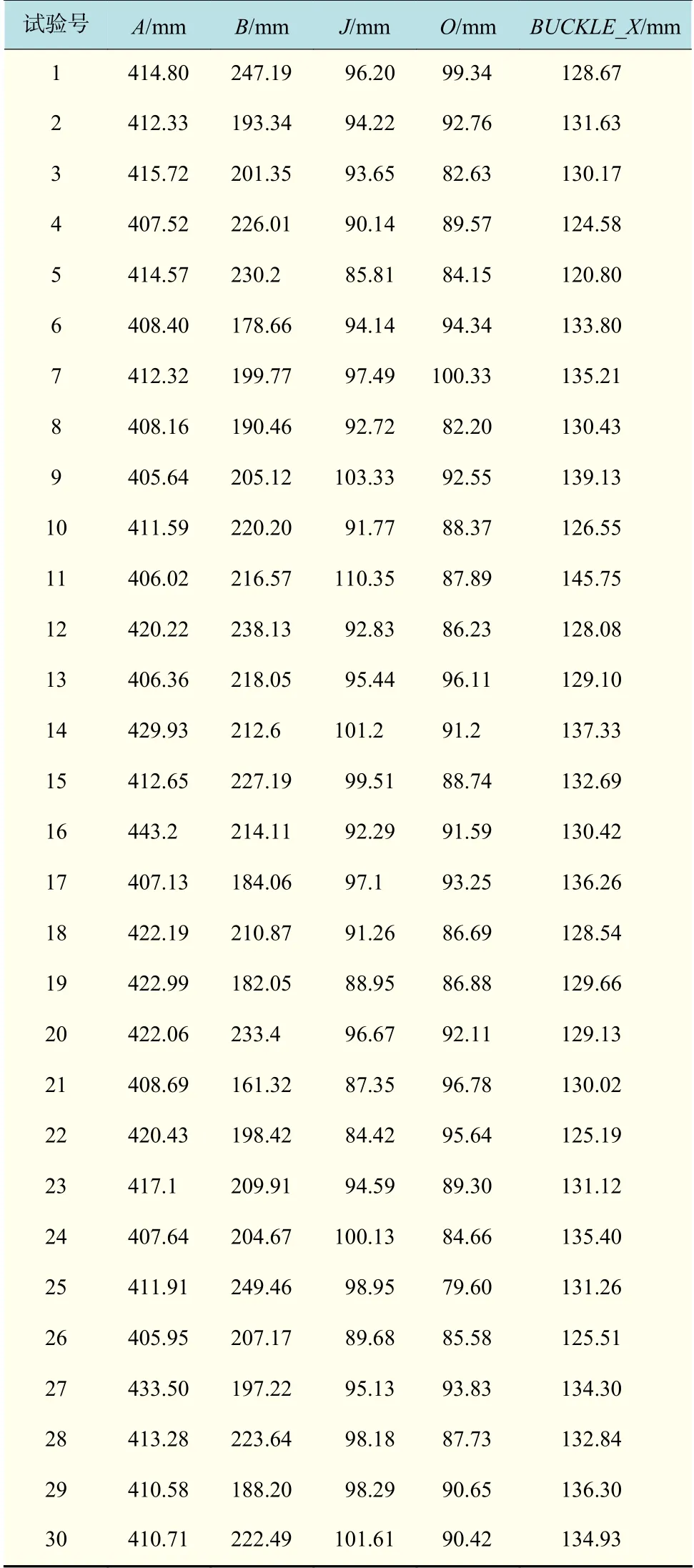
表2 安全带拉伸试验数据样本Tab.2 Data samples of safety belt tensile test

3 建模方法结果分析

选择采样得到前面20 组样本作为训练集，后面10 组样本作为预测集。利用粒子群优化算法来寻找最小二乘支持向量机核函数参数和正则化参数的最优值。设置粒子群的种群数为30，最大迭代次数为40，学习因子均为1.5，正则化参数的取值范围为[0.1,1 000]，核函数参数的取值范围为[0.01,1 000]。运用Matlab 软件运行PSO-LSSVM 模型，将寻找到的最优核函数参数和正则化参数重新更新，最终获得核函数参数为49.152 4，正则化参数为43.189 0。用训练好的PSO-LSSVM 优化模型对安全带拉伸试验进行预测。

为了验证和说明提出方法的有效性，采用BP 神经网络模型进行对比。其中BP 神经网络设置成输入层4 个节点、隐含层3 个节点、输出层1 个节点的网络，隐含层和输出层都是tansig 激活函数。预测结果如图5 所示，PSO-LSSVM 的预测结果与真实值更为接近，参数优化有效。因此采用PSO-LSSVM 建立安全带拉伸试验数学模型能有效地预测BUCKLE_X。

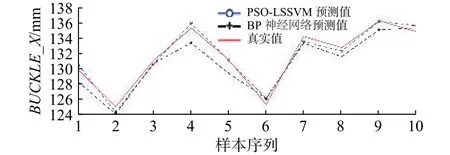
图5 PSO-LSSVM 与BP 神经网络建模对比Fig.5 Comparison of PSO-LSSVM and BP neural network modeling

为了评估回归模型的预测能力，通常采用两个重要指标来验证模型精度，即平均相对误差emr和均方误差ems，其值越小，代表模型性能越好。其中，平均相对误差是指预测值yˆi与真实值yi的绝对误差在真实值中所占比例的平均值，其计算公式为

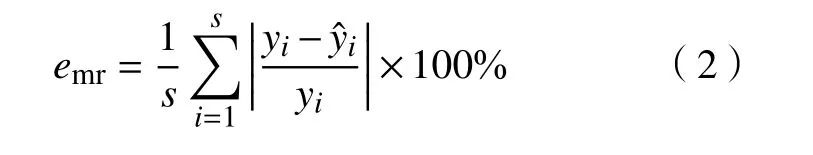
均方误差是指真实值与预测值差值的平方的期望值，其计算公式为

运用emr和ems两个回归预测性能指标，得到BP 神经网络和PSO-LSSVM 两种不同建模方法的emr和ems，其中PSO-LSSVM 和BP 神经网络预测结果的emr分别为0.38%和0.63%，ems分别为0.31 和1.07，如表3 所示。

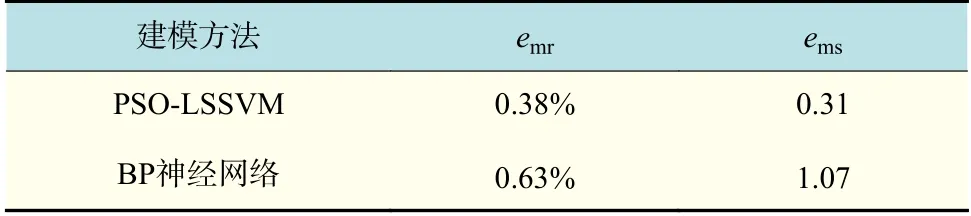
表3 PSO-LSSVM 与BP 神经网络的MRE/MSE 对比图Tab.3 MRE / MSE comparison between PSO-LSSVM and BP neural network

通过表3 对比可知，不论是平均相对误差还是均方误差，PSO-LSSVM 建立的数学模型精度都要高于BP 神经网络，其精度满足后续不确定度评定要求。在模型计算效率方面，采用4 核i5-7 300、主频2.5 GHz 的CPU 计算机运行模型，BP 神经网络运行时间虽然较长，但在可接受范围之内。

4 安全带拉伸试验不确定度评定

蒙特卡罗法（Monte Carlo method，MCM）[14-15]，与GUM 法不同，其采用分布传播方式来确定输出量的概率密度函数、估计值、不确定度以及包含概率区间。基于PSO-LSSVM 安全带拉伸试验的蒙特卡罗不确定度评定方法步骤如下所示：

步骤1蒙特卡洛法输入

a.定义需要被测量的量（输出量），安全带拉伸试验需要测量的量是BUCKLE_X；x1,x2,···,xd，安全带拉伸试验的不确定度来源是x1,x2,···,xd=(A,J,B,O)；

b.确定与输出量BUCKLE_X相关的输入量

c.建立输入量x1,x2,···,xd与输出量BUCKLE_X的测量模型；选PSO-LSSVM 建立输入输出关系的数学模型；

d.为输入量x1,x2,···,xd设定其概率密度函数；其中A符合韦伯尔分布，B，J，O符合正态分布；

e.选择蒙特卡罗试验次数M的大小；本试验选择试验次数M=106，因为M=106会为输出量BUCKLE_X提供95%的置信区间。

步骤2蒙特卡洛法传播

a.从输入量x1,x2,···,xd的概率密度分布函数中抽取106个样本值为第D个变量第R个样本值；

b.计算输出量BUCKLE_X的模型值(R=1,2···,M)。

步骤3蒙特卡罗法输出与结果

a.将这M个输出量按严格递增的顺序排序，通过排序模型得到输出量的分布函数如图6 所示。

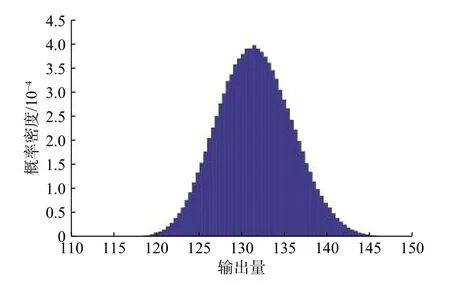
图6 输出量的概率密度分布函数Fig.6 Probability density distribution function of output

b.确定被测量BUCKLE_X的估计值y、标准不确定度u(y)，以及在给定包含概率95%时被测量BUCKLE_X的包含区间 [yl,yh]，如表4 所示。

表4 基于PSO-LSSVM 的安全带拉伸试验蒙特卡罗法不确定度分析结果Tab.4 Uncertainty analysis results of safety belt tensile test MCM method based on PSO-LSSVM

目前因为GUM 法使用普遍、计算简单等优点，其评定结果也可以用来作为参考。由GUM 法中的A 类评定可知，以30 组试验数据得到的BUCKLE_X结果均值当作估计值，平均值的标准偏差当作BUCKLE_X的标准不确定度，评定的结果如表5 所示。

表5 基于GUM 的A 类安全带拉伸试验不确定度分析结果Tab.5 Uncertainty analysis results of type a seat belt tensile test based on GUM

由表5 中A 类评定结果可知，除了估计值与蒙特卡罗模型得到的结果较接近外，标准不确定度和包含区间误差都比蒙特卡罗评定的误差大，标准不确定度从4.34 增加到4.95，增加了14%；95%包含的概率区间长度由16.94 增加到22.35，增加了32%。因为GUM 法规定的A 类评定在实际使用过程中只是对安全带拉伸试验BUCKLE_X位移进行了统计分析，没有体现出试验影响因素到试验结果的不确定度传递，且样本数目不多，因此GUM 法评定安全带拉伸试验不确定度的精度较低，也进一步证实了GUM 法不适用于复杂试验的不确定度分析。