用高考原题来组织课堂生成性片断教学①②——以2020年山东卷解析几何试题为例

李红庆 黄晓晓 喻 平

(1.海南华侨中学 570206；2.南京师范大学 210097)

2020年高考山东卷第22题，是继2019年全国Ⅲ卷考了圆锥曲线的一个通性：圆锥曲线C的准线l上一点D，自点D向C引两条切线DA，DB，那么切点弦AB过准线l对应的焦点，今年又考了圆锥曲线的另一个通性：圆锥曲线张角成直角的弦所在的直线过定点，即简称“张角成直角，弦过定点”．

在高考原题的启发下，教师应该引领高三学生去挖掘圆锥曲线的各种通性这一宝藏，因为这些圆锥曲线的通性都是人类科学智慧的结晶，所以挖掘宝藏需要倡导，需要传承．仅以刷题为目的组织教学，教学效果未必有成效．笔者认为应该借用高考原题来组织课堂生成性片断教学，每个片断都有生成性学生核心素养的目的，要建立片断间的内在联系，并且片断的切入点源于学生的通常思维，教师的责任是引领学生进行深层次的思考，找到解决问题的方法与手段．现仅以2020年山东卷解析几何试题为例，谈谈借用高考原题来组织课堂生成性片断教学．

1 通性简介与证明

设点A(x0,y0)是圆锥曲线C上一点，如果C的弦AM，AN满足∠MAN=90°，那么直线MN过定点R．

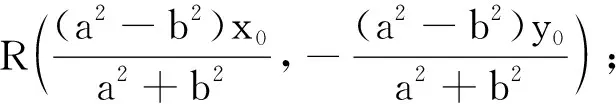
若C：y2=2px(p>0)，

则R(2p+x0,-y0)．

证明(片断教学设计)

仅证明椭圆C的情形：不失一般性，设直线MN的方程为y=kx+m(y0≠kx0+m)，M(x1,y1)，N(x2,y2),

(通常情况下是证明一般性情况，检验斜率不存在的特殊性情况)

得(b2+k2a2)x2+2a2kmx+a2m2-a2b2=0，

依根与系数关系，

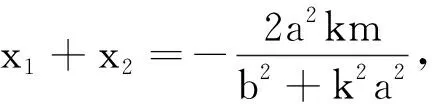
(1.1)

(1.2)

因为∠MAN=90°，于是

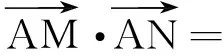
=(k2+1)x1x2+(km-ky0-x0)(x1+x2)

(1.3)

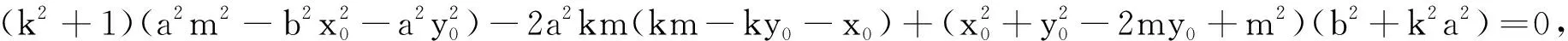
(a2+b2)m2+2(a2kx0-b2y0)m+(a2-b2)(kx0+y0)(kx0-y0)=0，

(1.4)

将式(1.4)分解因式，得

[(a2+b2)m+(a2-b2)(y0+kx0)][m-(y0-kx0)]=0，

解得

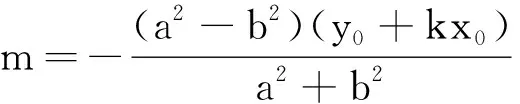
故直线MN的方程是

故直线MN经过点

若直线MN的斜率不存在时，不难检验结论也成立．

片断教学设计分享圆锥曲线的通性都需要一般情形来证明，证明过程中都涉及纯的字母算式的运算，考虑当前学生数学运算能力普遍偏弱，运算手段单一，培养学生数学运算能力这一核心素养就迫在眉睫.教师可以引导学生分析算式的归宿，即以算式的归宿作问题的驱使导向，这种运算技巧学生短期内掌握并不是很困难，关键是效果还非常好．

2 高考原题片断教学

2.1 高考原题

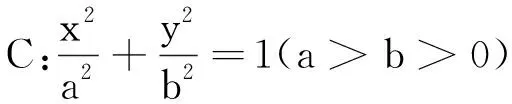
(1)求C的方程；

(2)点M，N在C上，且AM⊥AN，AD⊥MN，D为垂足．证明：存在定点Q，使得|DQ|为定值．

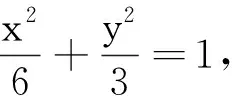
2.2 怎样寻找定点

从培养学生的逻辑推理这一核心素养的角度思考，希望学生要了解“张角成直角，弦过定点”这一通性，但并不是希望他们牢记定点的坐标，而是要把学生的大脑空间更多地留给逻辑思考，可以通过特殊情形找到定点，然后证明一般性．

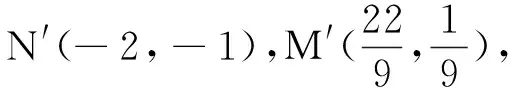
真正解题过程中，可以先通过草纸验算得到定点的位置，再根据题意选用恰当的方法得到结果．

图1

2.3 怎样利用定点解题

2.3.1 设直线MN的一般性方程

设直线MN：y=kx+m(2k+m≠1)，M(x1,y1)，N(x2,y2)，D(x0,y0)，

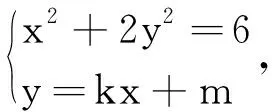
得(2k2+1)x2+4mkx+2m2-6=0，

依根与系数关系，得

于是

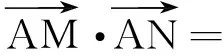
即得(3m+2k+1)(m+2k-1)=0，

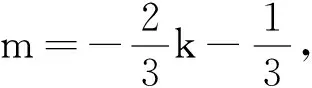
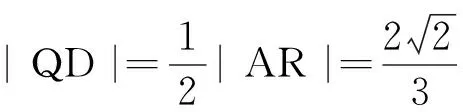
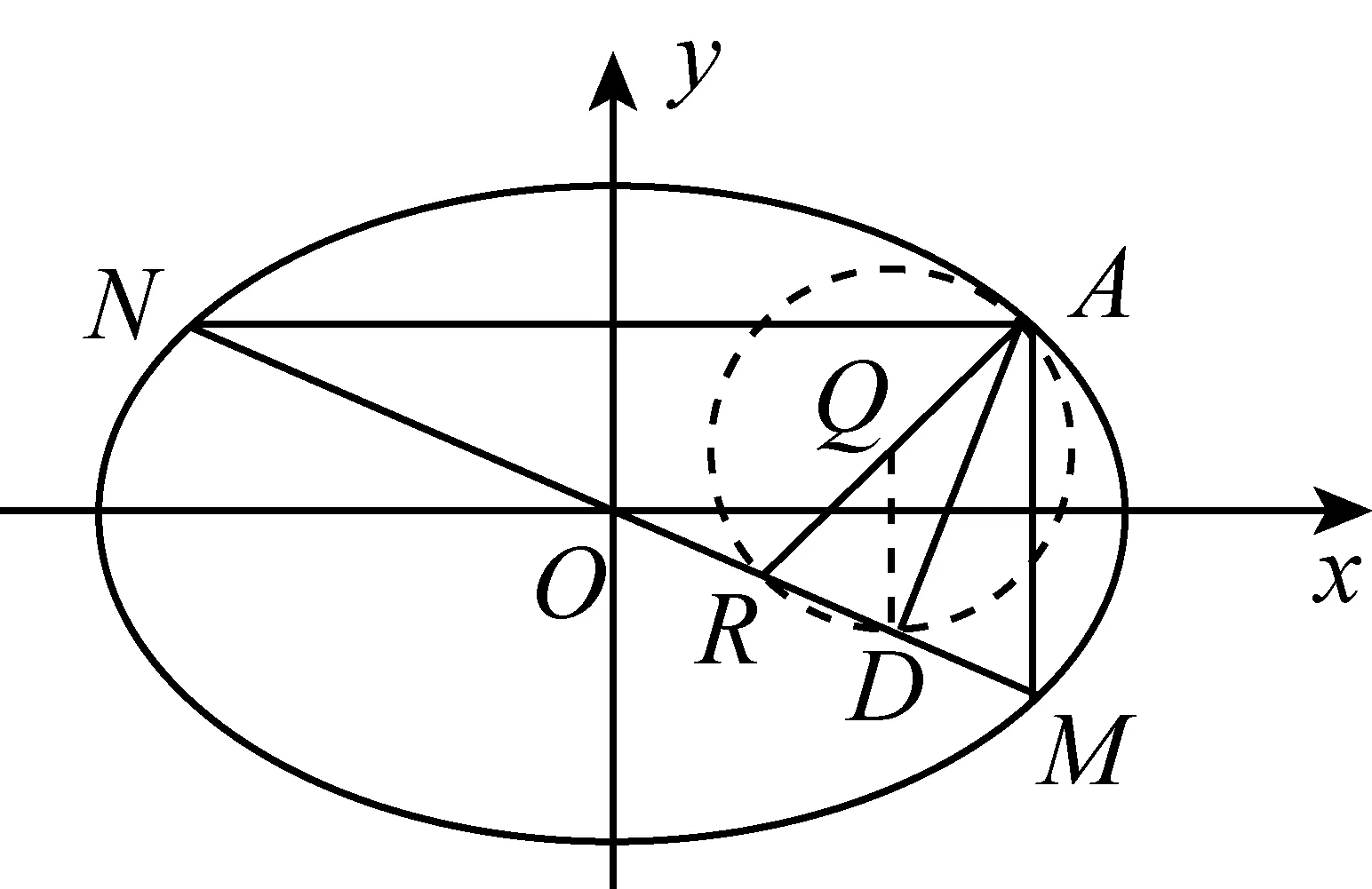
图2

上述方法是充分利用了定点R和平面几何的性质，如果没有注意到几何意义，纯代数方法也可以求解，下面设计没有利用定点的片断教学．

2.3.2 不利用定点的纯代数方法

(1.5)

(1.6)

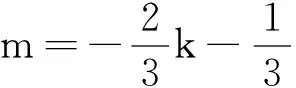
(1.7)

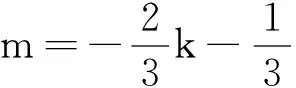
(1.8)

由式(1.7)、(1.8)，得

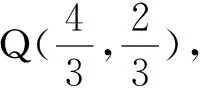
这个片断设计是基于发现[(k2-1)+2k]2+[(k2-1)-2k]2=2(k2+1)2的导向，而通过代数发现规律，要比通过几何性质发现规律往往要困难得多，当然如果没有定点的问题驱使为导向，纯代数计算也是天方夜谭.也可以把常量与变量换位思考，来设计片断教学．

本题还可以这样设计，点D在直线MN上，则y0=kx0+m，且k(y0-1)+(x0-2)=0，

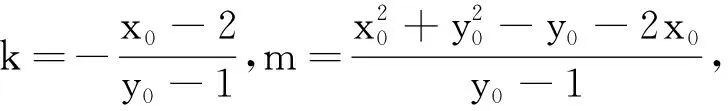
(问题驱使导向是把常量看作变量)

由AM⊥AN，得3m+2k+1=0，即得

2.3.3 充分利用定点解题

片断教学必须全方位考虑学生解题的各种切入的可能，解法不同，解题过程的难易差异很大，但这也不是绝对的，关键在于教师怎样引领，运算手段怎样选择，下面解法的切入点是多数学生会选择的，但如果没有定点作为问题趋使导向，没有整体思想，那么用这种方法解题，结果肯定是穷途末路．

设直线AM的方程y-1=k(x-2)，

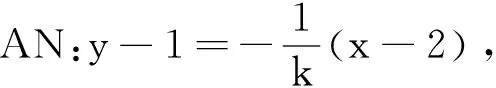
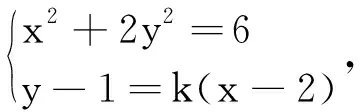
得(2k2+1)(x-2)2+(4+4k)(x-2)=0，

直线MN的方程是

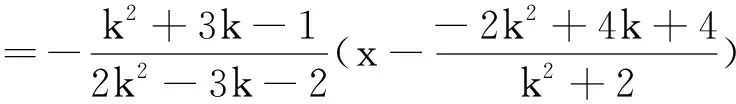
即得

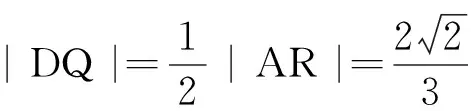
教学反思这种方法是为数不少同学解题的切入点，课堂片断教学是不能回避的，通过片断教学设计，向学生渗透整体思想方法，引导学生分析多项式运算的归宿，帮助学生养成关注定点的意识，如：多项式(2k2+1)(-k2+k)+(k2+2)(k+1)，算式的归宿是一元四次多项式，打乱运算规则，分别算出四次项-2k4，三次项3k3，二次项0，一次项3k和常数项2．

2.4 参数方程与射影定理

从辩证法观点来看，任何事物都有多种体现形式，这些形式都存在着内在的联系，有些性质容易发现，有些性质不易发现，往往不易发现的性质，使用起来可能更简捷．Rt△MAN内接于椭圆C，且点A为定点，AD⊥MN，容易发现的性质是射影定理．

设D(x0,y0)，直线MN的倾斜角为α，则直线MN的参数方程为

(1.9)

将式(1，9)代入C中，消去x，y得

(1.10)

又AM⊥AN，AD⊥MN，

由射影定理得|DA|2=-t1t2，

而|DA|2=(x0-2)2+(y0-1)2，所以

(1.11)

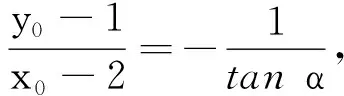
代入式(1.11)得

结束语高考试题是由命题专家命制的，它的科学性、示范性、经典性是不用质疑的．试题的各类解答专家心中都有数，但提供的解答必须是通性通法的解答．教师的教学就不限制于任何规定，可以充分挖掘各类解法，高三复习教学与其天天带着学生刷题，倒不如利用高考经典试题设计各种片断教学，来挖掘学生的潜能，激发学生的学习热情，培养学生的学科核心素养，让有限的课堂生成学生无限的能力，把数学教学提升到高层次的品味，让中国数学走向世界．