改进约瑟夫遍历和分段Logistic 映射的图像加密算法*

赵晓龙，李 博*，贾 芃，杨耀森

(1.中北大学仪器科学与动态测试教育部重点实验室，山西 太原030051；2.北方控制技术研究所，山西 太原030051)

随着互联网技术和多媒体技术的快速发展，人与人之间交流方式也发生了很大变化，数字图像能够生动地表达人们的意思，因此图像传输也成为信息交流的主要方法之一。 但传输过程如果不对图像进行加密处理，很容易被盗取和盗用。 数字图像其实就是二维的序列，其数据内容丰富，包含信息量大。 传统的加密算法会导致计算量大，效率低，难以适应现在图像加密的需求。 而混沌系统具有于随机性，遍历性，规律性等优点，同时具有初值敏感性和伪随机性等特征，可以产生复杂多变的伪随机序列，使得混沌系统非常适合应用于图像加密。

近些年来，伴随着许多研究者深入研究，混沌系统越来越多的被应用到加密图像中来。 但是现在已有的图像加密算法在实际使用中存在很大的安全隐患，还有很大的改进空间。 文献[1]提出了基于逻辑映射的图像加密算法，实际操作起来较简单，从结果来看具有良好的加密效果，但是仅仅是一种映射加密，安全性不足。 文献[2]利用Logistic 混沌映射对图像的像素位置置乱，在像素置乱中再次利用Logistic 混沌映射，通过二次混沌映射达到良好的加密效果，但这还是单一的混沌映射，算法秘钥空间小，不能有效抵御暴力攻击。 文献[3]中置乱与扩算方法采用的都是不同初始条件和不同的参数值生成的两个Logistic 混沌映射。 但仅仅依赖外部给定秘钥，容易被明文攻击，通过检索对应步骤的密码流可以被破解。 文献[4]利用效率较高的分块图像置乱算法，提高了加密效率，但没有解决Arnold 变换周期的问题，当扩散加密被破解后，置乱加密也会随之被攻破。

1 理论基础

1.1 约瑟夫遍历

约瑟夫环问题原本是一个数学问题:假设有n个人他们围着一张圆桌坐在一起，给他们编号从1到n。 任意取一个编号n0，从第n0个人由1 开始报数，数到a 的那个人出局；由出局后的下一个人开始继续从1 开始报数，数到a 的人接着出局；遵循这一规则进行重复报数，一直持续到圆桌最后一个人也出局，求出最后出局的人的序号。 运用递归算法可以解决这个问题，首先把m 个人的序号重新编号由1 到n-1，根据式(1)计算，最后出局的人的编号为f(n)+1。

例如当n ＝8，m0＝1，a ＝4，约瑟夫遍历的轨迹图如图1 所示。

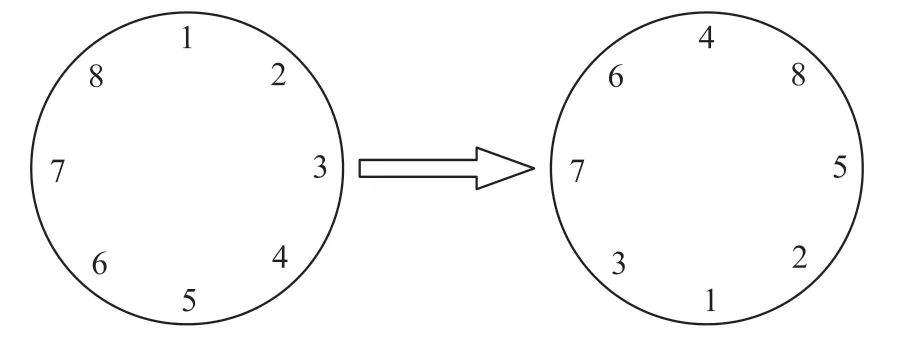
图1 n=8 时的经典约瑟夫轨迹

根据上述可知约瑟夫环问题包含三个变量，起始位置m0，出局的间隔a，参与总人数n。 该序列由于具有周期性，容易被人通过其周期性的特点而被破解，本文为了使得该变换产生的置乱空间更大，提出增加两个变量i 和t 作为参数，i 是约瑟夫遍历映射的报数间隔，t 表示报数的方向，t≥0 为顺时针方向，t＜0 为逆时针方向。 即:

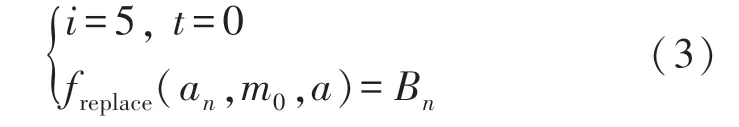
引入这两个参数可以增加秘钥空间，改善了其周期性的特点而且将加密图像与秘钥联系起来，从而提高了加密图像的安全性。

1.2 Logistic 映射

Logistic 混沌映射其实就是生态学中的虫口模型，可以用如下公式表示:

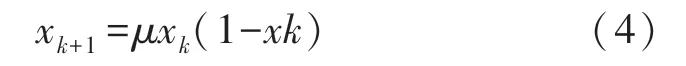
当3.569 9＜μ≤4 时，Logistic 混沌映射此时处于混沌状态。 在该公式下生成的伪随机序列是非周期性、非收敛而且对初值十分敏感[13]。 如图2 所示。

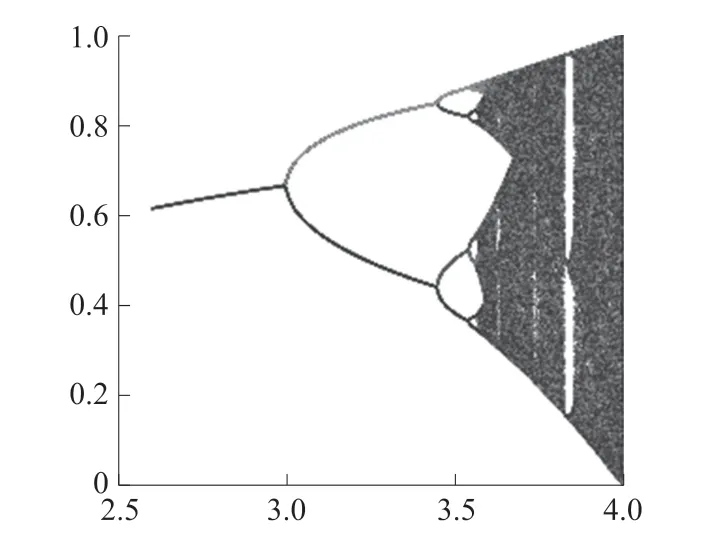
图2 Logistic 混沌映射

Logistic 混沌映射属于一维混沌系统，作为图像加密中最常见的一种方法[6]，它的特点是系统参数较少，混沌区间小，函数形式简单，混沌复杂程度低，由上图可以看出Logistic 混沌映射的参数范围较小，这是该混沌系统现有的缺点，通过对该混沌映射的公式改进可以有效扩大其参数范围，如文献[5]中改进Logistic 混沌映射的方程式:

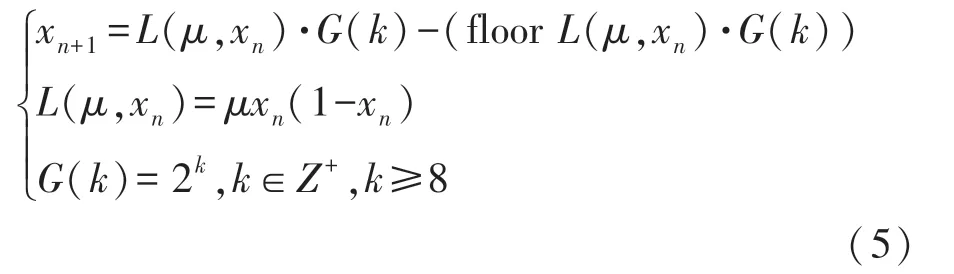
式中:floor 函数是向下取整函数，式(5)是式(4)的一种改进形式，L(μ，xk)就是μxk(1-xk)。

经过改良Logistc 混沌映射公式，混沌映射参数μ 的取值范围得到有效扩大，在0＜μ≤4 的范围之间该公式有良好的混沌状态，在[0，1]的范围之间混沌序列呈现出均匀分布，但该混沌序列仅仅依靠μ和x0的初值，为了进一步增强混沌序列的伪随机性，将上述混沌映射设计成一个分段函数，将原始图像的部分元素值作为一个秘钥参数引入到方程式中，经过改进后的分段Logistic 映射公式可表示为:

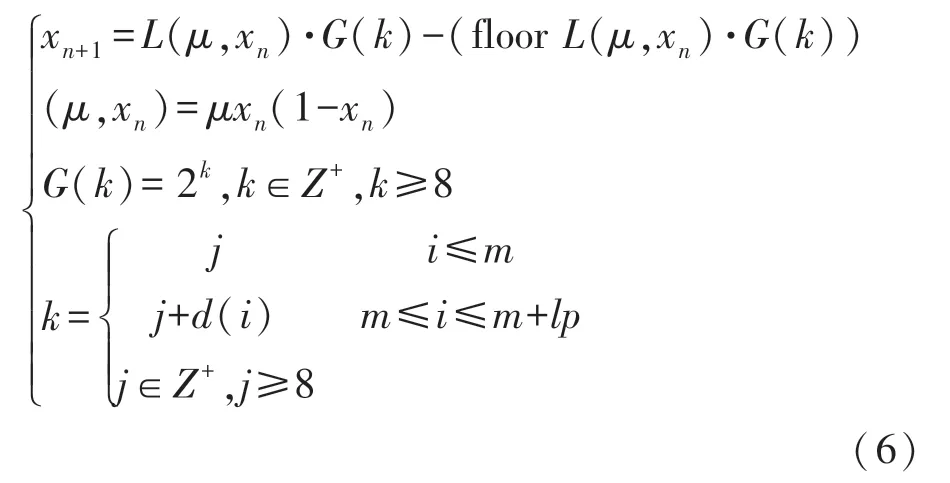
这里i 是迭代次数，m 是因为Logistic 映射会存在暂态效应故舍去混沌序列的前m 项，d(i)是加密图像的元素值，lp 是待加密图像的像素总数。 与Logistic 混 沌 映 射 相 比， 分 段 Logistic 映 射 的Lyapunov 指数更高，说明其混沌性更好，表明加密后的混沌序列更具有随机性。

2 加密算法的设计

2.1 像素全局置乱

输入原始图像的256×256 的灰度图像peppers，令lp ＝256×256，将灰度图像peppers 按照列优先的顺序将图像转化成一维向量P1，P1＝{a1，a2，…，alp}且初始参数取值范围分别为:序列An长度∈[0，lp-1]，取合理的初始参数m0＝1，step ＝11，i ＝5，t＝0，将向量P1代入式(3)可得

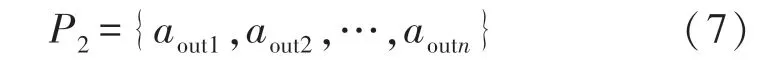
通过上述对P1进行置乱，可以得到图像P。

2.2 矩阵扩算和像素值替换

(1)将图像P 分解为两个4 位的矩阵H 和L，矩阵H 与L 分别是高四位和低四位的位平面矩阵。

(2)输入参数μ1，x1，利用式(6)和矩阵H 迭代n+lp 次得图像的部分元素值d(i)，舍去前n 个值得到秘钥序列K。

(3)利用序列K 对矩阵L 进行位置扩散，得到矩阵L1，置乱方法如下式:

序列K 按照从大到小的顺序排列可以得到位置序列T:T＝{t1，t2，t3，…，tlp}，利用序列K 对矩阵L进行位置扩散。

(4)选取随机序列K 小数点后第9～11 位数字，对16 取模，得到0 ～15 的一个伪随机整数序列K1，用K1与H 作异或运算，得到高四位位平面的加密矩阵H1。

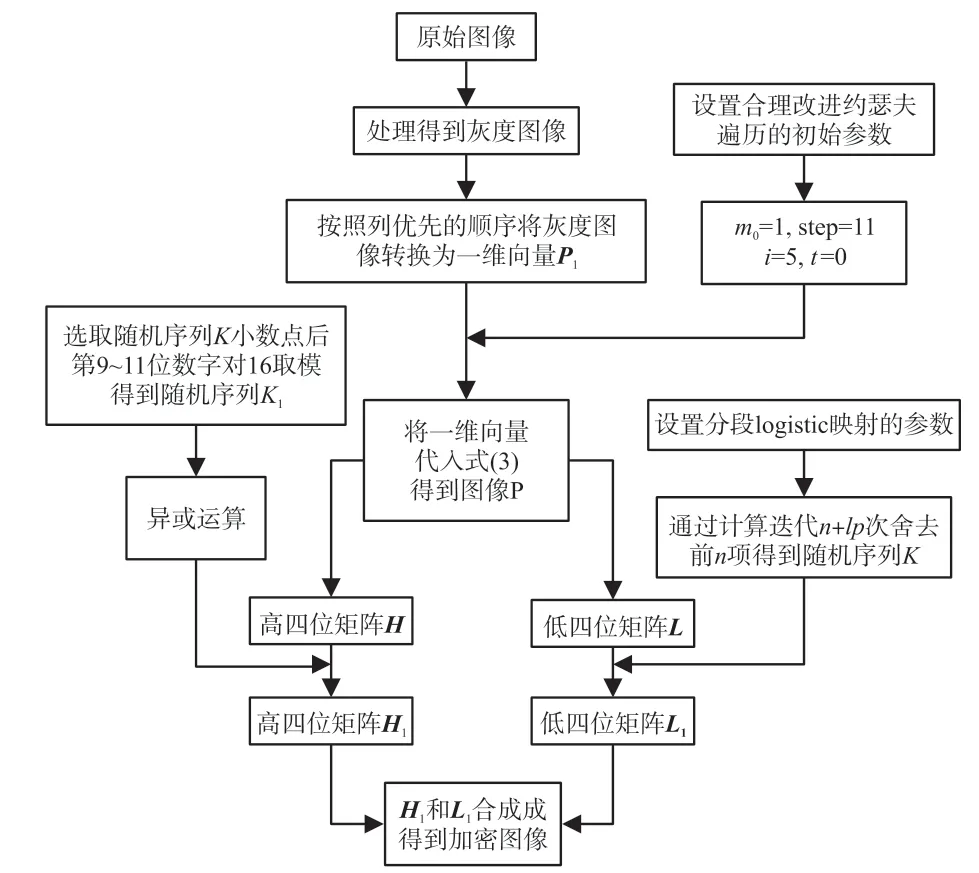
图3 加密算法流程图

(5)把H1和L1合成一个8 位矩阵，得到最终加密图像E。 加密算法流程图如图3 所示。

2.3 解密算法

解密的过程就是加密的逆过程，只要按照之前加密的方法输入正确的秘钥参数，进行相反的操作就可以解密出原始图像。

3 仿真结果

本文采用了大小为256×256 的peppers 图像作为加密图像，采用Win7 系统的电脑，内存为4G，通过MATLAB2014b 进行仿真实验，利用MATLAB 做完仿真试验后得到如下的图像结果。 图4 为peppers 的灰度原始图像，图5 为改进约瑟夫遍历置乱后的图像，图6 是加密后的最终图像，图7 是解密后正确图像。

图4 原始图像

图5 置乱图像

图6 加密图像

图7 解密图像

4 算法分析

4.1 秘钥空间分析

一个良好的加密算法必须拥有足够大的秘钥空间[7]，本文的算法秘钥是由两个不同的混沌映射控制的，秘钥的组成有μ1，x1，m0，step，i，假设计算机的储存精度是10-15，所以该改进算法的秘钥空间为1075，另外还有约瑟夫报数的方向与它的间隔等，因此该算法的加密空间估计为10100，因此可以更好地抵御穷举等暴力攻击。

4.2 密文统计特性

4.21 直方图分析直方图可以直观地反映图像不同灰度级像素出现的频率[8]，原始图像的明文分布具有自己独有的特殊性，在不同的区域明文分布大不相同，像素分布不均容易被人破解，通过加密方法可以有效改善图像像素的分布，可以很好地对明文图像进行隐藏，达到了预期加密的效果。

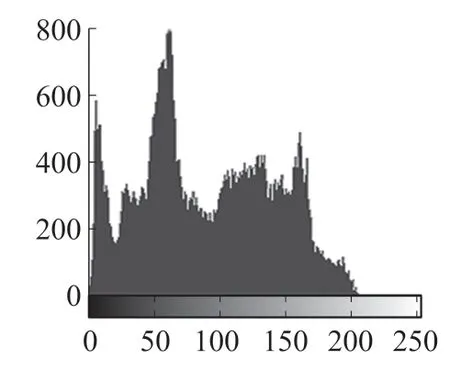
图8 明文灰度直方图

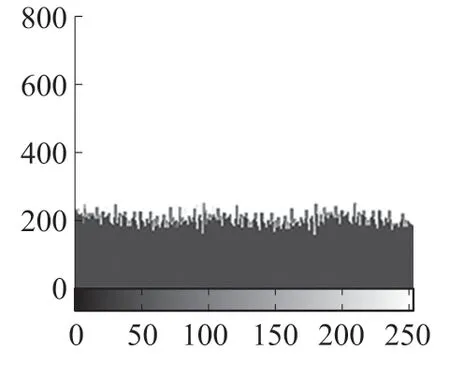
图9 密文灰度直方图

4.2.2 信息熵

信息熵是加密算法中一个常用的量化指标，也可以评价一个系统的复杂程度，加密图像像素分布越均匀，图像的信息熵越大，信息熵最大值为8，由式(9)可以计算出加密图像的信息熵:

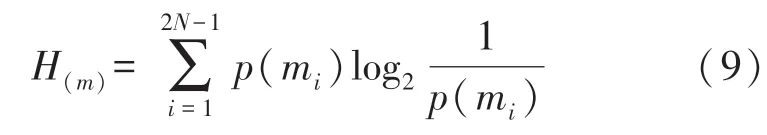
式中:mi是图像灰度值，本文改进后的算法信息熵为7.997 5，图像加密效果与其信息熵的值越接近8，图像加密效果越好，说明每个像素值分布的概率非常相似，加密效果好，结果表明熵攻击并不能对加密图像造成破坏。

4.2.3 相邻像素点的相关性

图像加密前后的相关性也是衡量加密效果的一个重要参数[9]，明文图像通常是较为清晰的画像，图像相邻像素点之间的相关性高，而密文图像破坏了原来图像的相邻像素的相关性，密文相关性越接近于0，加密效果越好。 利用仿真实验，以垂直，水平，对角线三个不同方向为例，x，y 是相邻两个像素值的灰度值，根据式(10)随机选取1 000 对相邻像素计算其相关性:

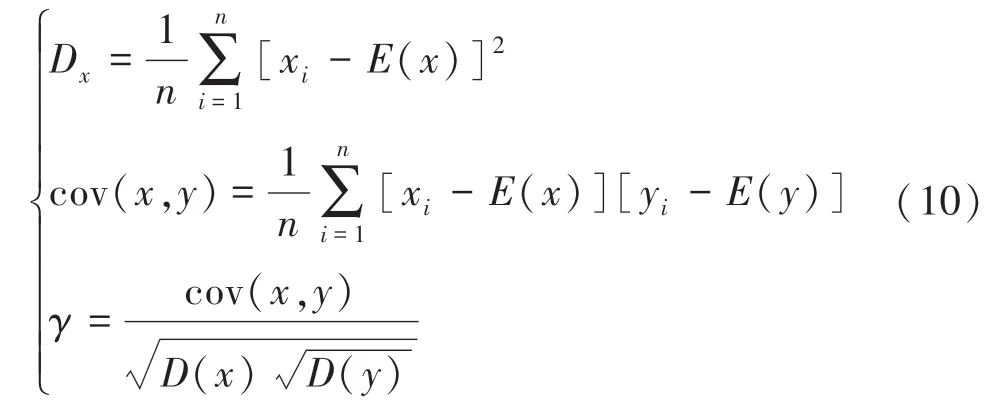
式中:Dx是方差，E(x)，E(y)是相邻像素值的期望，n 是像素点的个数，cov(x，y)是它的协方差；γ 是相关系数。

图像加密前后在三个不同方向像素点的分布情况可由图10～图12 表示，这是分别从三个不同角度分析得出其相关性的分布。 图10 ～图12 中左边代表了原始图像在3 个不同方向像素点分布的密度，右边代表加密图像在3 个不同方向的像素点分布的密度。 从图中可以看出无论是水平方向，垂直方向还是在y ＝x 方向，原始图像的点都集中在对角线的范围内，呈线性分布，显而易见明文图像的相邻像素点具有很强的相关性。 而加密图像的像素点的分布是随机无序的分布在图中，所以加密图像的相邻像素点相关性很弱。

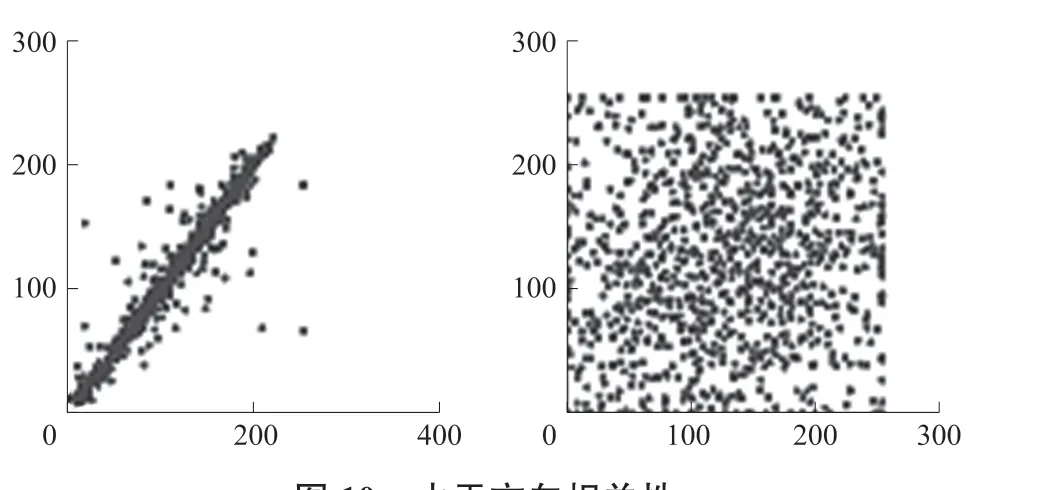
图10 水平方向相关性

图11 垂直方向相关性

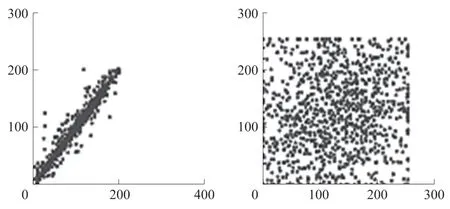
图12 对角线方向相关性

从表1 中可以看出，原始图像与加密图像的相关系数的值差别很大，相关系数的数值越接近1，图像相邻像素的相关性越高，反之数值越小相关性越弱[12]，所以可以得出结论:加密图像的相邻像素点之间几乎没有相关性。 跟其他算法比较，该算法相关系数小，具有良好的扩散性，加密性能更好。

表1 相邻像素点的相关系数的比较

4.2.4 差分攻击分析

差分攻击是通过对加密前后图像特定的区域进行比较分析来攻击密码算法的。 像素变化率NPCR(the number of pixels change rate)，归一化平均变化强度UACI(the unified average changing intensity)，其中NPCR 表示的不同密文图像在相同位置上灰度值互不相同的比率，而UACI 则表示不同密文图像之间的平均变化密度，通常用于图像加密抗差分性分析。 如果单个像素点的变化可以导致加密图像产生明显的改变，说明算法可以有效抵御差分攻击。 所以NPCR 和UACI 是有效分析抗差分攻击的重要指标，由公式(11)和(12)计算可得:

为了研究加密算法能否抵御差分攻击，可以通过改变原始图像中像素点来判断。 随机选取1 个像素点，对选出的像素值加1，对改变像素值后的图像进行加密，利用式(11)和式(12)计算。 通过计算得出NPCR 和UACI 的平均值分别是99.62% 和31.59%。 说明当原始图像中某个像素值被改变后，会使加密后的图像NPCR 变化接近100%，计算出UACI 的值也在31%以上。 通过上面的分析可以得出该加密算法可以有效抵御差分攻击。

5 对比分析

为了验证文章算法的创新性和其良好的加密效果，通过算法多样性，明文与密钥是否相关，加密时间，信息熵还有密钥空间进行分析，使用大小为256×256 的Lena 图像作为参考，通过与文献[10-12]进行对比分析结果如表2 所示。

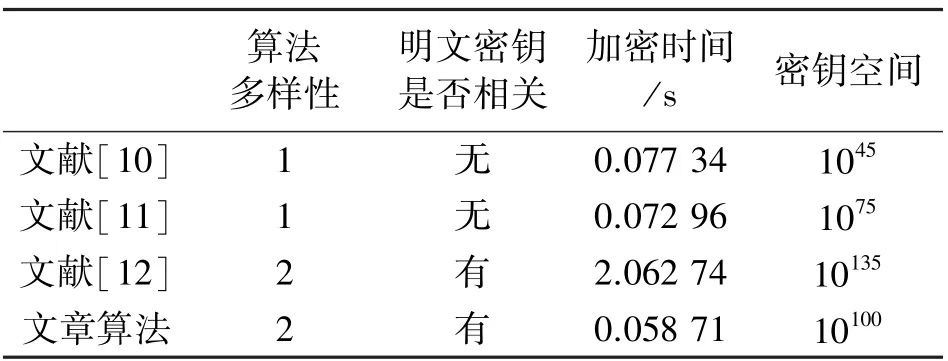
表2 不同算法对比分析结果

由表2 可以看出文献[12]和本文都是利用不同的加密算法进行加密，算法的多样性使得加密的安全性能大大提升。 而文献[10]和文献[11]只是单一映射，容易被人破解。 文献[12]和本文都引入明文参数，使得轻微的改变明文像素会使得密钥大大改变，从而提升了密钥破解难度，而文献[10-11]的密钥与明文无关，关联性不强，抗差分攻击弱。

表中的加密时间是利用MATLAB2014b 生成107个序列值的平均时间，通常密钥空间≥2100(相当于1030)。 由表2 可知文章的密钥空间处于中上水平，可以有效抵御穷举攻击。 虽然文章密钥空间不如文献[12]，但是由于改进Logistic 映射简单，生成序列时间段，因此本文加密时间会更短，可以较好地满足实际需要。

6 结束语

文章针对网络信息和图像传输安全提出了改进约瑟夫遍历和分段Logistic 映射的加密算法，通过利用改进后约瑟夫遍历进行图像的置乱操作，对于置乱后的图像进行分解，分解为两个四位的高低矩阵，对高四位矩阵进行分段Logistic 映射置乱，对低四位矩阵进行异或处理，再将高四位矩阵与低四位矩阵进行结合，最终得到加密图像。 该算法利用约瑟夫遍历，增加了该算法的加密空间，引入报数间隔和报数方向改善其周期性的特点，对分段Logistic 映射引入加密图像的元素值d(i)，使得秘钥不仅仅从外部获取。 仿真实验结果表明，该算法的秘钥空间大，加密后的图像置乱度高，将图像中的元素引入算法中，使得抗攻击性强，而约瑟夫遍历引入报数间隔和报数方向使得该置乱方法难以从周期性破解，安全性更高，因此改进后的算法加密效果更好。