基于二元多项式与中国剩余定理的多秘密分享方案

2015-01-04黄科华

长沙大学学报 2015年2期

黄科华

(泉州幼儿师范高等专科学校初等教育系，福建泉州362000)

秘密分享方案的主要目的是用来解决在特定用户(准入结构)中分享一个秘密.一个秘密分享方案(SSS)主要包含以下几个方面:秘钥分发者D，参与用户集合P，准入结构Γ，秘钥空间S，分配算法和恢复算法.

Shamir［1］和 Blakley［2］与1979年分别独立提出了(t，n)门限秘密分享方案，通过该方案，n用户中只要有t个及以上的人合作就能合成秘钥，而少于t个用户就得不到秘钥的任何信息.当然，两个方案都存在许多不足的地方，如1)秘密份额是一次性的，不能重复利用;2)秘钥分发者的权利过大，有可能导致秘钥分发者的欺骗，比如发送无效的份额;3)每次只能共享一个秘钥，秘钥的信息不够大等.在两个方案的基础上，Asmuth和Bloom［3］在1983年提出的基于中国剩余定理的门限方案;Brlckell［4］等人在1991年提出了理想化的秘密共享方案;黄科华［5］结合单向函数和二元多项式的方案解决了秘钥的一次性使用的问题，本文正是在此基础上，利用中国剩余定理，提供了一个多秘密的分享方案，而且在这个方案中，引入可验证的秘钥机制，来避免秘钥欺骗.

1 预备知识

1.1 陷门单向函数

陷门单项函数h(x)满足以下两个条件，(i)给定x，能够容易地计算y=h(x);

(ii)给定y，计算x=h－1(y)是困难的，但是如果知道陷门，可以容易地计算出y.

陷门单向函数可以选择离散对数函数或者RSA函数等.

1.2 中国剩余定理

设整数 m1，m2，…mn两两互质，对于任意整数 s1，s2，…sn，方程组:

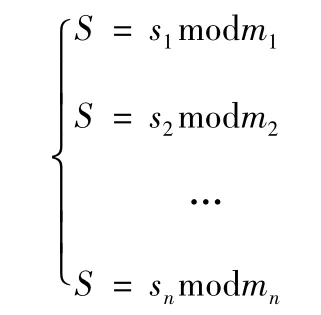
2 基于二元多项式与中国剩余定理的多秘密分享方案

2.1 秘钥生成和分发阶段

设有n个用户为P1，P2，…Pn.每个Pj自己选取一个向量作为自己的私钥(且yij≠ymn，i≠m 或者 j≠ n)，并计算 h(yij)，i=0，1，2，…t，j=1，2，…n.其中h(x)为无碰撞陷门单向函数，由秘钥分发者D选取并公布，陷门信息由D掌握.

设s1，si，…sn是需要分享的多个秘钥，秘钥分发者D选择n个互质的整数 m1，m2，…mn，通过中国剩余定理得到modM的唯一解S.

D构造一个二元多项式f(x，y)，表达式如下:

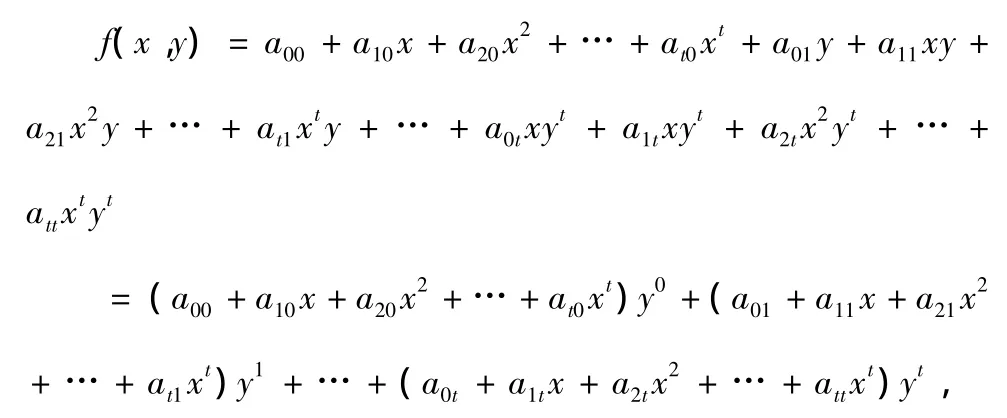
并使得a00=S(常数项为秘钥S)

D 计算 f(xi，yij)，i=0，1，2，…，t，j=1，2，3，…，n.并公布.

2.2 秘钥的合成过程

不妨设 f(xi，yij)=Aij，i=0，1，2，…，t，j=1，2，3，…，n

三个月前，他们瞒着所有的人，写了一份分手协议，分配了财产。但他们彼此各退一步，商定等孩子三年后上了大学，再公布于众。按照协议规定，他们互不打探干涉对方的私生活，仍在一个屋檐下或者另租居所，不过，每月孩子回来的那天必须琴瑟和鸣夫唱妇随。

t+1个用户合作可以通过以下方式恢复二元多项式，取得S.

从公告牌中的 xi，(i=0，1，2，…，t)可以得出下列方程组:

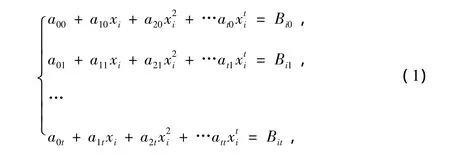
即

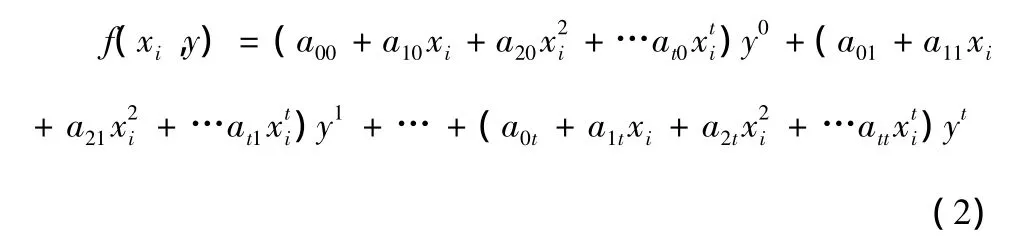
t+1 个用户可以拿出 yij0，yij1，…，yijt，

其中 0 ≤ j0，j1，…，jt(均为正整数)≤ n，i=0，1，2，…，t

代入(2)式可得:

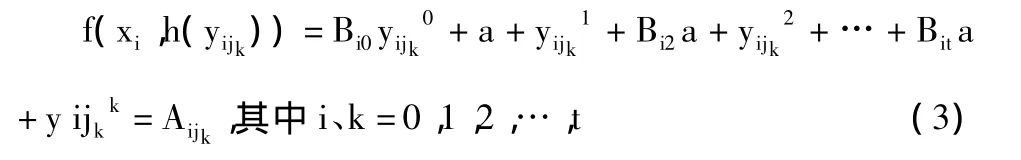
(3)可以写成方程组:

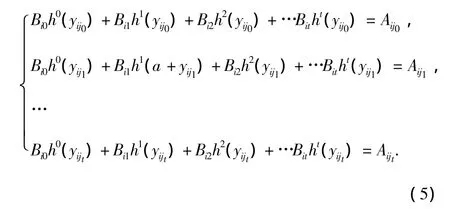
也即是以下的矩阵:

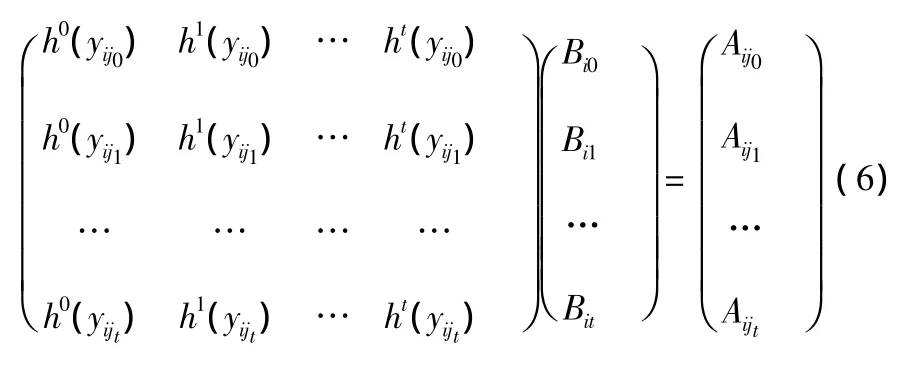
由(2)式可得下列方程组:

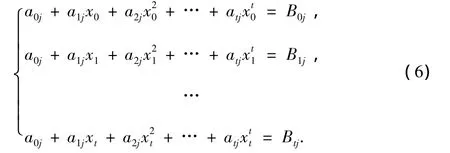
其中 j=0，1，2，…，t.

写成矩阵即为:

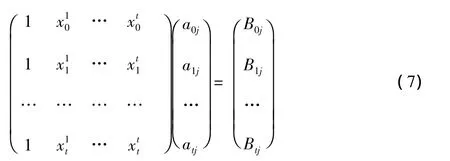
由于xi≠xj，i≠j，所以系数矩阵为范德蒙矩阵，能够解出唯一解:

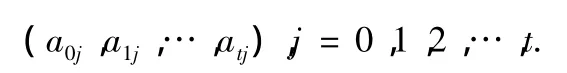
因为能够合成整个二元多项式，取得S.

取得S后，每个用户可以再从公布的m1，m2，…mn中解出所有的秘钥 s1，si，…sn.

3 分析

3.1 满足门限性

从方案中可以看出，该方案为(t+1，n)门限方案，t+1个人合作可以顺利恢复秘钥，而少于t+1，就无法从方程组4(或者矩阵 5)中恢复出(Bi0，Bi1，…，Bit)，i=0，1，2，…，t，因而，也无法从方程组6(或者矩阵7)中恢复出系数(a0j，a1j，…，atj)，j=0，1，2，…，t，故不能得到密钥 S.