相关衰落MIMO 信道下的联合天线子集选择*

杜文龙，黄 余

(1.江苏电子信息职业技术学院计算机与通信工程学院，江苏 淮安223003；2.圣路易斯大学研究生院，菲律宾 碧瑶2600)

多输入多输出(Multiple-Input Multiple-Output，MIMO)技术[1]可以明显提高系统性能。 这种多天线提供的额外自由度可通过空间复用[2]用于提高比特率，或通过空时编码技术[3-4]改善分集阶数。 然而，多天线部署需要多个射频(Radio Freqency，RF)链路，这些RF 链路通常是非常昂贵的。 因此，采用具有低成本、低复杂度技术的多天线具有相当大的吸引力，最优天线子集选择就是这样的技术，天线单元的选择可在发射机和/或接收机上使用，发送/接收是通过最优子集进行的。

关于天线选择的早期研究大多集中在多输入单输出信道或单输入多输出信道，主要包括混合选择/最大比合并算法[5]。 近年来，人们对天线子集选择技术在MIMO 信道中的应用研究产生了极大的兴趣。 文献[6]基于信道容量最大化准则，采用两个二进制编码字符串分别表示发射端和接收端天线选择的状态，提出将二进制猫群算法应用于多天线选择中；文献[7]基于二进制粒子群算法，提出了一种新的MIMO 系统联合收发端天线选择算法，以达到提高信道容量的目的；文献[8]表明天线选择技术可应用于低阶信道以提高信道容量；文献[9]研究了阵列天线中利用天线子集选择及智能算法等来实现信息安全传输的保密技术；文献[10]提出了一种采用线性接收机的空间复用系统的误码率最小化天线选择算法；文献[11]提出了采用Alamouti 码传输的天线选择提高平均信噪比(Signal Noise Ratio，SNR)的精确表达式。

本文采用空时编码技术Alamouti 码，基于相关衰落MIMO 链路上的精确信道知识(Accurate Knowledge for Channel，AKC)和统计信道知识(Statistical Knowledge for Channel，SKC)提出了2 种新的天线子集选择算法和性能分析的综合理论。 当AKC 可用时，选择算法选择天线子集以使信道Frobenius 范数最大化，从而使得数据流的接收SNR 最大化和瞬时误差概率最小化；当SKC 可用时，选择算法选择天线子集以使矢量化信道的协方差的行列式最大化，从而使全部可能信道实现的平均误差概率(Average Probability of Error，APE)最小化；而且进一步表明，对于某些信道模型，联合子集选择是解耦的，允许独立于接收天线而选择发射天线，或者反之。

1 信道与信号模型

考虑一个点对点无线链路，有MT个发射和MR个接收RF 链路，并假设有KT(KT＞MT)个发射天线单元和KR(KR＞MR)个接收天线单元，选择KT个中的MT个和KR个中的MR个天线单元并分别连接到发射和接收RF 链路，如图1 所示。 经过MIMO 信道(大小为MT×MR)的发射和接收是通过这些选择的天线子集来完成的，在接收机端假设正确的信道状态信息和最大似然解码，此外，还已知发射机端和接收机端的信道统计值；先给出文中所用到的记号，全部向量和矩阵皆为粗斜体。

XT:X 的转置运算；

XH:X 的厄米特转置运算；

‖X‖F:X 的Frobenius 范数；

[X]ij:X 的第(i，j)个元素；

X⊗Y:X 与Y 的克罗内克积；

E{·}:求数学期望；

vec{X}:向量化矩阵X；

det{·}:求方阵的行列式值。

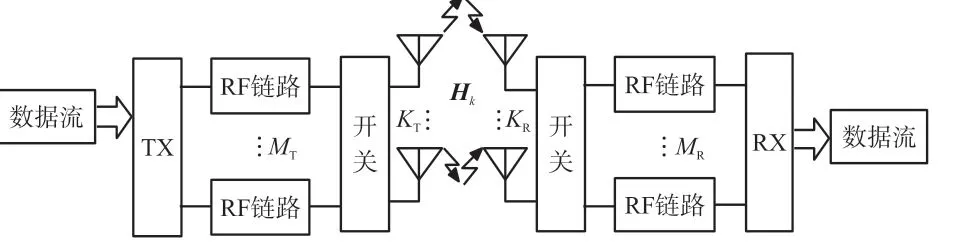
图1 MIMO 系统及天线选择示意图

1.1 信道模型

令HK(大小为KR×KT)为信道矩阵，假设信道为平坦瑞利衰落。 实际测量表明发射和接收之间存在相关性，因此假设在发射机和接收机之间存在相关散射，且信道矩阵可以建模为引起接收相关性的矩阵和引起发射相关性的矩阵的乘积，即:

1.2 信号模型

由于只有MT个发射和MR个接收RF 链路，将所选择的天线子集间的(MR×MT)信道表示为H，将所选择信道的发射和接收协方差矩阵分别表示为RT和RR，即H 是HK的一个子集，RT是RTK的一个主子矩阵，RR是RRK的一个主子矩阵。

令第k 个时刻从MT个发射天线发射的符号为s1[k]，…，sMT[k]，于是得到信号模型如下:

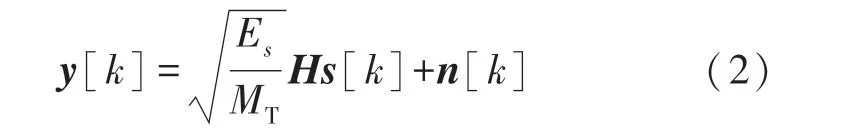
式中:y[k](大小为MR×1)为接收信号向量，Es为总的发射信号能量，s[k]＝[s1[k]，…，sMT[k]]T为时刻k 发射的信号向量，n[k](大小为MR×1)为加性白高斯噪声向量，H 为所选择的发射和接收天线单元之间的MR×MT信道矩阵。

假设每帧为T 个符号周期长，则将T 个接收到的信号向量叠加起来得到:

2 基于AKC 的天线子集选择

2.1 OSTBC 和最优选择

2.1.1 OSTBC

正交空时分组码(Orthogonal Space-Time Block Code，OSTBC)给出了相关衰落信道中的最大分集阶数，编码和解码是以接收数据流的SNR 实现的[3]，即:

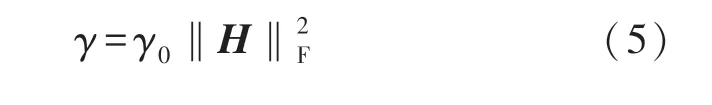
式中:d 为常数，依赖于所采用的星座图。 从式(5)和(6)可以看出:最大化信道Frobenius 范数会使SNR 最大化，从而使瞬时误差概率即误符号率最小化，所以可根据这一结果提出天线选择算法如下。

2.1.2 天线选择算法

2.2 算法性能分析及仿真

2.2.1 平均SNR 分析

选择算法选择KT个发射天线单元中的MT个，以使信道的Frobenius 范数最大化。 重写接收数据流的SNR 式(5):

式(10)和选择算法选择具有最大Frobenius 范数的列表明，我们需要采用式(8)的PDF 和式(9)的CDF 的KT个i.i.d.卡方变量中的MT个最大变量的一阶统计值。

式中:γ0MRMT为没有天线选择(或随机天线选择)时采用OSTBC 的平均SNR。

对于接收天线选择(这时KT＝MT，KR＞MR)的分析容易通过用KR替换式(12)中的KT和用MT替换式(12)中的MR来得到。

图2 所示为采用Alamouti 码传输MT＝2 时发射天线选择(KT≤MT，KR＝MR)的平均SNR 增益g 的曲线。 可以看到，选择带来的平均SNR 增益g 改善是非常明显的。 此外，还可看到，当采用较少数量的接收天线时，发射天线选择的增益g 更高，这是因为随着接收天线数量的增加，列平方的Frobenius 范数越来越接近，从而降低了选择的影响。

图2 基于AKC 的发射天线选择的平均SNR 增益g

图3 所示为采用Alamouti 码传输MT＝2 时的接收天线选择(KR≤MR)的平均SNR 增益g 的曲线。可以看到，对于MR＝2 时的接收天线选择增益g 与采用2 个接收天线的发射天线选择的增益g 是相同的(见图2 和图3 中最上端的一条曲线)，这是必然的结果，因为从前面的分析来看，这两种情况是相同的。

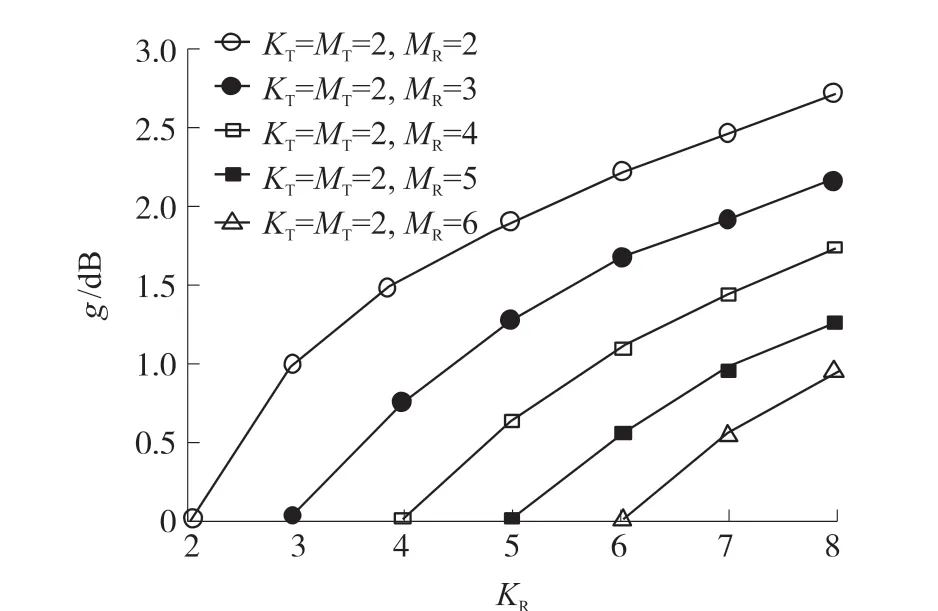
图3 基于AKC 的接收天线选择的平均SNR 增益g

3 基于SKC 的天线子集选择

基于SKC 的天线子集选择不同于AKC 中选择天线集是最小化瞬时误差概率，而是最小化平均误差概率(Average Probability of Error，APE，即平均误符号率)。

3.1 平均误差概率与天线选择

3.1.1 平均误差概率表达式

令S(i)为发送的码字，S(j)为与发送码字不相同的其他码字，定义第(i，j)个误差矩阵为Ei，j＝S(i)-S(j)。 根据切诺夫界(Chernoff bound)，解码码字S(j)而不是S(i)(i≠j)的概率由成对误差概率(Pairwise Error Probability，PEP)给出为:

在高信噪比下，它会降低到:

式(19)表明了分集阶数对发射和接收协方差矩阵的秩的依赖关系。 特别地，分集阶数是由RR和RT的秩的乘积决定，RT的秩减少会使分集阶数降低，对于RR的秩来说反之。

式(19)和式(20)的结果对应于发射和接收天线子集的一种特定选择。 通常，对于不同的选择，发射和接收协方差矩阵是不同的，而目标是选择使式(20)最小化的天线集。

3.1.2 天线选择算法

3.2 算法性能分析及仿真

令RTopt和RRopt分别为对应于最优天线子集的发射和接收协方差矩阵，RT和RR为任何其他选择子集的对应协方差矩阵。

3.2.1 编码增益

假设Ropt和R 都是满秩的，根据式(20)，性能改善可以表示为:

在高信噪比下，这种效应与系统中的编码一样，因此将这个增益称为编码增益，近似如下:

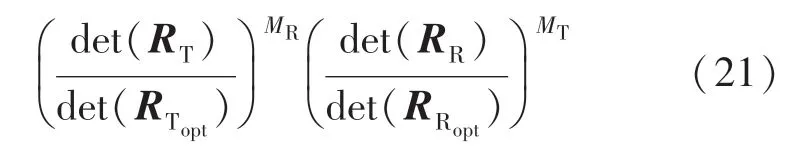
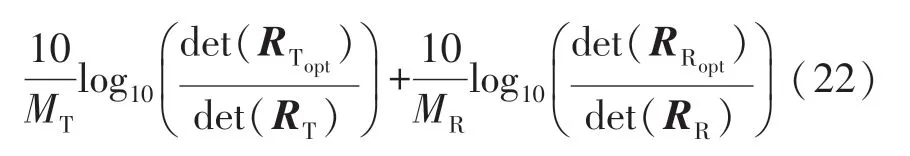
3.2.2 分集增益

在极其相关的信道条件下，有可能天线的某些子集是完全相关的，这时，发射或接收协方差矩阵(或两者)可能是低秩的。 因此基于统计值的选择也可以通过增大误符号率曲线的斜率来改善分集增益。 令r 和t 分别为RR和RT的秩，则分集阶数增益为ropttopt-rt，ropt和topt分别为RRopt和RTopt的秩。

当两个协方差矩阵都是满秩的病态R 和良态Ropt时，例如，对于特定的信噪比区域，不同的天线集曲线有不同的斜率，即使对应的协方差矩阵有相同的秩。

为了验证选择算法的性能，假设相关衰落和由式(1)表示的信道模型，且对于相关衰落，采用GWSSUS 模型[13]生成式(23)和式(24)中的协方差矩阵:

图4 所示为接收选择(KR＝3，MR＝2，KT＝MT＝2)在2 种情形下的平均SER 曲线，假设2 种情况下的发射协方差矩阵恒等，接收协方差矩阵分别为RRⅠ和RRⅡ；图5 所示为采用发射和接收联合选择(KR＝3，MR＝2，KT＝3，MT＝2)的系统的平均SER 曲线，其中发射协方差矩阵为RRⅠ，接收协方差矩阵为RRⅡ。

图4 基于SKC 的接收选择情形Ⅰ和Ⅱ的SER 曲线(Alamouti 码，4-QAM)

图5 基于SKC 的联合选择的SER 曲线(Alamouti 码，4-QAM)

对于接收选择，基于最大化协方差的行列式选择算法预测情形Ⅰ的最佳接收天线为1 和2(或2和3)，情形Ⅱ的最佳接收天线为1 和3，如表1 所示。 从图4 可见，2 种情形对应的SER 曲线明显是最优的，因此理论预测是准确的；此外，可以看到情形Ⅱ中明显的分集效应，这是因为接收天线1 和2的协方差矩阵条件很差(但仍然有秩2)，而天线1和3 的协方差矩阵条件更好；图5 所示联合发送和接收选择的4 种可能情形。 算法预测发射天线1 和2 以及接收天线1 和3 是最优的，从图5 可见，得到的仿真结果也验证了预测。

显然，基于统计值的选择可以显著地提高性能，在仿真所考虑的实例中提高了2 dB～4 dB。 一般来说，这些增益将依赖于RTK和RRK的准确结构。

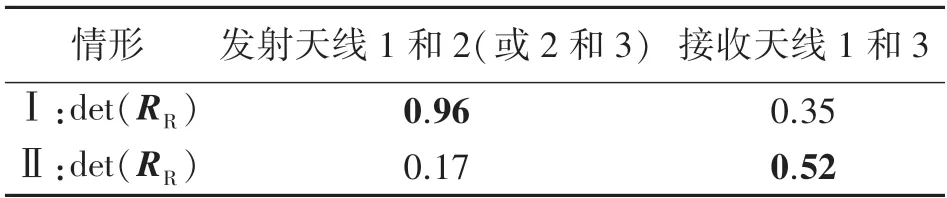
表1 仿真情形的选择规则

4 结束语

本文探讨了相关衰落信道中采用空时编码的最优MIMO 子集选择问题，提出了基于AKC 和SKC的选择算法和性能分析，并给出了仿真结果来验证算法的性能；此外，本文研究仅限于平坦衰落信道，在存在传播延迟的情况下，选择增益可能会由于信道中充分的频率分集而降低，这是我们今后研究的一个主要问题。