金属膜电阻失效前后概率分布及可靠性分析*

2021-03-23王倩男何文辉

电子器件 2021年1期

王倩男，何文辉

(中国计量大学机电工程学院，浙江杭州310018)

金属膜电阻是膜式电阻器(Film Resistors)中的一种，是采用高温真空镀膜技术将镍铬或类似的合金紧密附在瓷棒表面形成皮膜，经过切割调试阻值，以达到最终要求的精密阻值，然后加适当接头切割，并在其表面涂上环氧树脂密封保护而成。工厂在生产电阻时，因为工艺条件，设备条件，原材料的波动，导致达不到预期的可靠性指标[1]。要提高电阻的可靠性，需要知道电阻失效的原因，对失效模型进行量化判定，进而促进产品质量的提升，此外，金属膜电阻可靠性指标的量化分析，对批量生产时控制产品质量的稳定性、一致性均有重要意义。鉴于金属膜电阻可靠性较高的特点，本文探讨了步进应力加速寿命试验在金属膜电阻可靠性指标分析，及电阻失效原因查找方面的方法与理论模型构建。

近年来，一些学者对此做了相关研究。张放等[2]采用不同程度的高温高湿试验对片式厚膜电阻器长期可靠性及失效模式进行了研究分析，并提出正确涂覆三防漆能够有效提高电阻在高温高湿下的可靠性水平。曹玉保等[3]对金属氧化膜电阻进行了失效分析，成功准确地找到了金属膜电阻的失效部位，并从电气角度分析了金属膜电阻的失效过程，总结了提高金属膜电阻的可靠性的方法。 David Han[4]在连续检查和间隔检查两种不同的故障检查模式下，使用基于条件块独立性的随机终止时间的递归关系，得出了在渐进式I 型检查下一般k 级逐步应力加速寿命试验的预期终止时间。谭勇等[5]建立了步进加速寿命试验数据处理方法步骤，针对步进应力加速寿命试验的设计提出了建议。陈愿等[6]使用定时截尾恒定应力加速寿命试验方法来评估电子元器件在一定可靠度下的贮存寿命，建立威布尔分布加速寿命模型，采用极大似然法进行参数估计，得到模型未知参数的极大似然估计结果，最后外推得到正常温度下的贮存寿命。强苗[7]对电子元器件的失效模型与可靠性试验方法进行了探讨。柏小娟[8]在已有的筛选标准的前提下，对电子元器件制定了两类通用筛选流程，设计了典型型号筛选方案，并研究了国产器件的补充筛选。 Nga Man Jennifa Li 等[9]对电子元件保质期的评估方法和失效原理进行了研究，根据失效机理及其类别，选择失效模型的物理性质和可接受标准来评估保质期，提出了一种基失效机理(POF)的大多数电子元器件的寿命评估方法。 Romit Kulkarni 等[10]研究了在循环热载荷作用下，表面贴装在印刷电路板(PCBs)上、热固性注塑封装的典型电子元件的可靠性，并对电子元件的特征寿命进行了统计计算。

综上，可以发现现有的研究大多集中在电子元器件的筛选，可靠性分析，失效模型以及寿命的估计，但是对电子元器件失效前后的阻值概率分布情况，以及哪种失效模型会造成这种概率分布少有研究，本文从电阻失效前后的阻值概率分布试验及步进应力加速寿命试验两部分来展开分析讨论，企图从失效概率分布的角度给出电阻质量特性。

1 实验过程

1.1 实验样品选取

RJ14 金属膜电阻具有轴向引线、涂漆绝缘、色环标志，具有体积小、精度高、温度系数小、耐湿性好、耐热性好、阻值稳定可靠等特点，适用于各种交、直流电路，本文将其作为实验研究对象。本次试验所用设备包括:示波器一台，万用表一个。示波器可调最高电压为31 V，而本次试验采用步进应力加速寿命试验，每伏电压加压时间为20 s，需要小功率，小阻值的电阻才能保证在31 V 前会冒烟损坏，所以选取了精度为0.1%，阻值25 Ω 的RJ14 金属膜电阻，并从50 个电阻中随机选取了20 个进行试验，电阻的帽盖结构图如图1 所示，主要参数表如表1 所示。

图1 RJ14 电阻帽盖结构图

表1 RJ14 电阻主要参数表

1.2 电阻失效前后的概率分布试验

首先，取20 个电阻，分别测量20 个电阻的阻值，并分别对电阻步进加压，步进电压为1 V，每伏保压时间为20 s，记录电阻冒烟损坏时的电压与阻值。图2 为冒烟损坏的电阻。

图2 电阻冒烟损坏

合格电阻阻值为24.8 Ω、25 Ω、25 Ω、25 Ω、25.1 Ω、25.1 Ω、25.1 Ω、25.1 Ω、25.1 Ω、25.1 Ω、25.1 Ω、25.1 Ω、25.2 Ω、25.2 Ω、25.2 Ω、25.2 Ω、25.2 Ω、25.2 Ω、25.2 Ω、25.3 Ω。

冒烟损坏电阻阻值为21.1 Ω、21.3 Ω、21.3 Ω、21.4 Ω、21.7 Ω、21.8 Ω、21.9 Ω、22.0 Ω、22.1 Ω、22.3 Ω、22.4 Ω、22.4 Ω、22.5 Ω、22.6 Ω、22.6 Ω、22.9 Ω、23.0 Ω、23.0 Ω、23.0 Ω、23.2 Ω。

其中9 V 时失效3 个，10 V 时失效17 个。收集到数据后，对数据进行分析，画出其频率直方图以及累积频率直方图，由频率直方图可判断大致属于威布尔分布，然后对其进行假设验证。分布检验采用的是F 检验，经过检验后假设成立，并利用最小二乘法对参数进行估计。

1.3 步进应力加速寿命试验

试验中采用的电阻为RJ14 金属膜电阻，额定电压为2.5 V，施加的应力S1、S2、……、S8分别为3 V、4 V、……、10 V，每V 电压保压时间为20 s，在9 V时冒烟损坏3 个，10 V 时17 个，记录失效时间，推出失效时间的概率分布函数F(t)＝1-e(t/146.6)45.54，属于威布尔分布。

对威布尔分布下的步进应力加速寿命试验数据进行统计分析，首先进行数据折算处理，将步进加速试验数据得到的r 个数据全部折算到应力水平S1下，得到

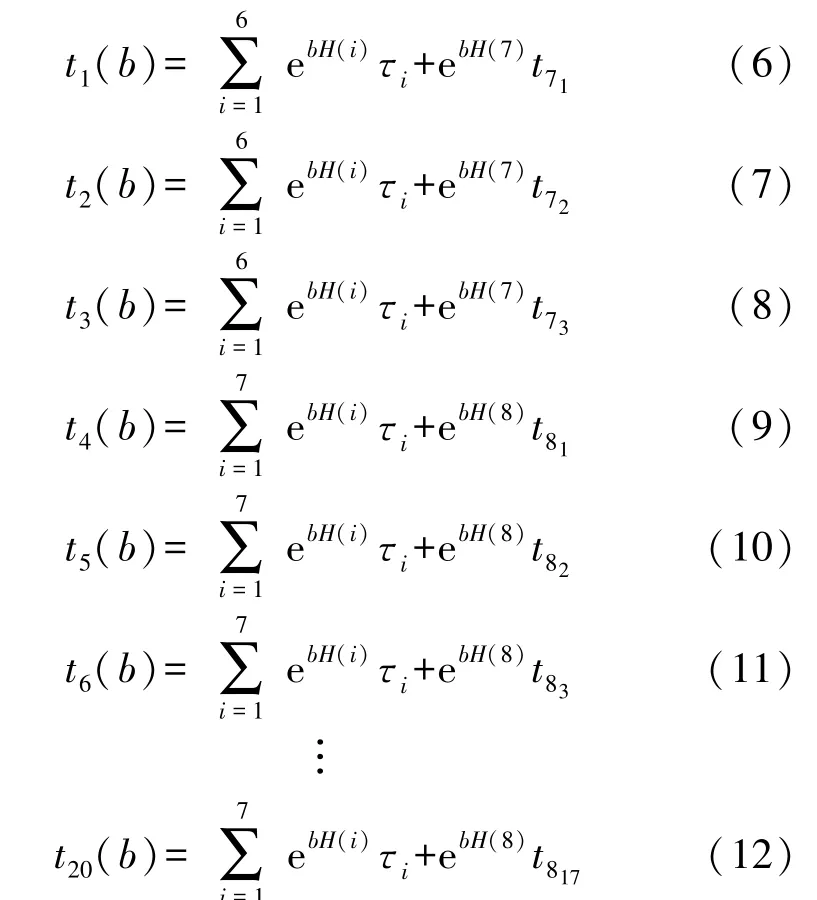
式中:τi是在应力水平Si下的工作时间，m 为形状参数，ηi为特征寿命，t1～t20为应力S1下的失效时间(单位:s)，t71为应力S7下第一个电阻损坏的时间，t71～t817以此类推。本文选用逆幂律加速模型lnηi＝a+bφ(Si)，a，b 为待估参数，为方便起见，记φi为φ(Si)，即φi＝ln(Si)；H(i)＝φ1-φi，这批数据中含有未知数b，将这批数据记为t1(b)＜t2(b)＜…＜t20(b)。

由逆矩估计法得

式中:C(n，r，i)＝[-0.035 2，-0.037 7，-0.038 9，-0.039 4，-0.039 2，-0.038 4，-0.037 1，-0.035 2，-0.032 7，-0.025 9，-0.025 4，-0.020 5，-0.014 3，-0.006 7，0.003 0，0.015 4，0.032 1，0.056 0，0.095 1，0.228 8]，r＝20。

将m-1的估计代入式(13)中，可得到只含一个未知参数b 的方程，接着通过数值方法计算b 的估计值b(，再代入式(14)中求得m(，然后可得应力水平S1下特征寿命η1的估计值η(1:

2 实验结果和讨论

2.1 电阻失效前后的概率分布试验结果

在电阻失效前后的概率分布试验中，电阻的失效原因是持续的加压使电阻受到应力损伤，属于积累损伤模型，且应力撤走后电阻仍然失效，在这种失效模型下阻值概率分布函数为F(t)＝1-e(t/22.52)41.32，合格电阻的阻值概率分布函数为F(t)＝1-e(t/25.16)293.3。图3 为冒烟损坏电阻的阻值概率分布图，图4 为合格电阻的阻值概率分布图。

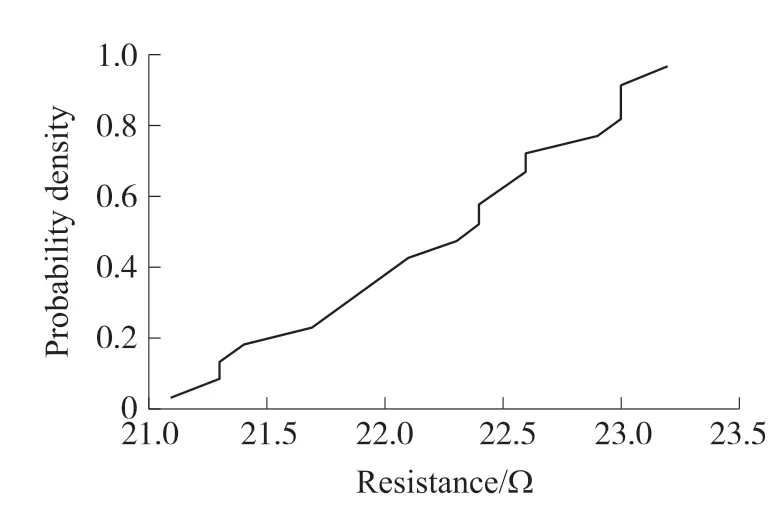
图3 冒烟损坏电阻的阻值概率分布图

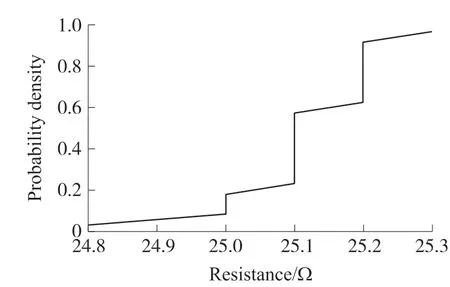
图4 合格电阻的阻值概率分布图

2.2 步进应力加速寿命试验结果

2.3 讨论

要提高电阻的可靠性，首先需要知道电阻可能的失效原因(发生率)，会导致的失效效应(严重度)，以及现行管制方式所能检测出此失效模式的能力(难检度)，任何改进措施都是为了降低其发生率，严重度和难检度，增加设计确认/检验只能降低难检度，若要降低发生率，只能通过设计更改消除或降低失效模式发生原因，降低严重度。针对积累损伤模型采取相应的处理方法，不断试验发现故障，并消除故障，不断扩大破坏裕度和工作裕度，可以有效加强耐环境能力，提高产品可靠性。

根据上述对金属膜电阻的研究，由于二极管与电容被击穿时阻值也会发生变化，或许可将本文对金属膜电阻的试验方法扩展到二极管与电容的研究中，对二极管与电容进行电阻失效前后的概率分布试验以及步进应力加速寿命试验，得到失效前后的阻值概率分布图、概率分布函数以及正常应力下的概率分布函数与可靠性指标，从失效概率分布的角度给出二极管与电容质量特性。

下一步，可以研究二极管与电容失效前后是否属于同一分布，若属于不同分布，找出这种差异的原因；然后对比金属膜电阻、二极管、电容三者失效后的概率分布是否属于同一分布，若属于不同分布，同样找出差异原因。