一个具有无限多吸引子共存的新混沌系统的动力学分析及其电路实现*

孙 亮，罗 佳*，乔印虎

(1.池州职业技术学院机电技术系，安徽 池州247000；2.安徽科技学院机械工程学院，安徽 凤阳233100)

自从1963 年发现Lorenz 混沌吸引子以来[1]，各种新混沌系统不断被发现和研究，如1999 年陈关荣教授等人[2]提出的Chen 系统，2002 年吕金虎教授等人[3]提出的Lü 系统、2004 年刘崇新教授等人[4]提出的Liu 系统以及其他的扩展混沌系统[5-6]。 近年来，研究发现，许多的混沌系统具有共存吸引子特性，即多稳定性[7-9]。 具有多稳定性的混沌系统比一般混沌系统具有更大的不确定性，在信息加密和保密通信等领域具有极高的应用价值[10-11]。 特别是2016 年包伯成教授等人[12]在一个忆阻电路中发现了超级多稳定性现象，即在确定的混沌系统中存在无限多个吸引子共存特性。 此后，超级多稳定性现象在各种混沌系统中被陆续发现和研究[13-16]。 本文提出了一个新的三维连续混沌系统，该系统仅含有2 个非线性项，不仅具有一般混沌系统的特性，重要的是其能够表现出丰富的超多稳定性，即在确定的参数情况下，不同的初始值能够得到无限多种不同的混沌吸引子。 同时为了在实际工程中更好地应用此系统，设计了系统的实现电路并进行了仿真实验，实验结果验证了数值仿真的正确性。

1 新的三维混沌系统

新系统动力学方程为:

图1 混沌吸引子相图

式中:x，y，z 为3 个系统状态变量，a，b，c，d 为4个正的系统参数，xsin(z)和xy 为2 个非线性项。当参 数a ＝1，b ＝0.5，c ＝12，d ＝0.3，初 值 为(2，2，2)时，系统具有双翼混沌吸引子，如图1(a)、(b)所示，图1(c)为y ＝0 时的x-z 彭加莱截面，可以看出彭加莱截面为不规则的分段曲线，说明此时系统处于混沌状态。 图1(d)为系统3 个变量随时间变化的时序图，可以看出产生的序列具有无周期性，进一步证明此时系统处于混沌状态。

2 新系统的动力学分析

2.1 耗散性

通过对系统(1)中3 个非线性方程等式分别求偏导，可以得到系统的散度为:

显然，当a＞0 且b＞0 时，∇V 恒小于0，系统(1)是耗散的。 在此条件下，系统以指数形式收敛dv/dt＝e-(a+b)，这意味着，当t 趋于无穷大时，系统轨线上每一个小体积元收敛到0，系统的轨迹逐渐趋于一个有界的吸引子。

2.2 平衡点稳定性

令系统(1)等式右边等于0，可以得到系统的平衡点状态方程如下:

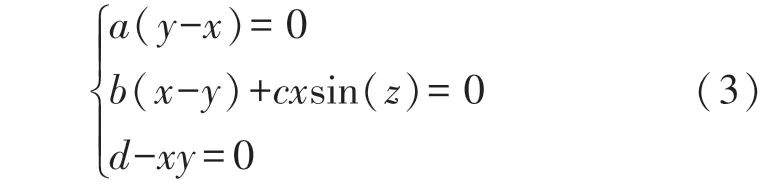
解平衡方程(3)可以得到无限多个系统平衡点，如下所示:

式中:k ＝0，±1，±2，±3，±4，…。 计算系统Jacobi 矩阵为:

所有平衡点P 均有以下特征方程:

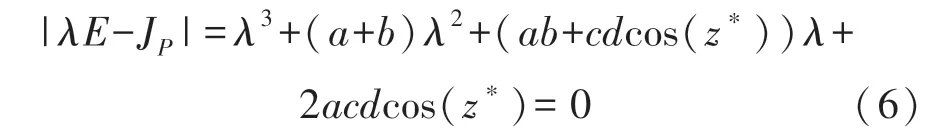
显然，对于所有正参数，基于劳斯稳定性判定定理，系统(1)的所有平衡点均具有不稳定性特性。

2.3 参数对系统特性的影响

当保持系统参数a ＝1，b ＝0.5，c ＝12 不变，初值分别设为(2，2，2)和(2，2，-2)，系统随参数d 变化的分岔图如图2 所示，其中纵坐标为x 变量最大值。在图2 中，紫色表示初值(2，2，2)条件下系统产生的分岔结果，蓝色表示初值(2，2，-2)条件下系统产生的分岔结果。 从图2 可以发现，随着参数d 从0开始正向增大，系统动力学轨迹通过正向倍周期分岔路径从周期行为快速进入到混沌状态，直到d ＝0.64。 需要指出的是，在此混沌区间内系统存在少数窄周期窗特性。 随后系统又开始从混沌行为反向倍周期分岔进入周期行为，并在d ＝0.76 时通过切分岔路径快速演变为混沌行为。 随着d 的进一步增大，系统再次通过反向倍周期分岔途径在d ＝1.1 时进入到周期状态，随后系统保持周期状态稳定不变。此外，从图2 中还可以明显的观察到两个特点:一是系统的混沌吸引子幅度与d 密切相关；二是在部分d 的取值范围内存在共存吸引子现象。 为了进一步证实系统(1)的参数变化特性，图3 给出了初值(2，2，2)条件下，系统随参数d 变化的Lyapunov 指数谱，当d 在(0.1，0.64)与(0.74，1.1)范围内，系统Lyapunov 指数分布为(+，0，-)，根据李雅普诺夫指数判定定理，说明系统是混沌的。 从图3 可以看出，系统在d ∈(0，0.1)，d ∈(0.65，0.73)，d ∈(1.2，1.5)，区间内以及d ＝0.4，d ＝0.46，d ＝0.592 时，Lyapunov 指数分布为(0，-，-)，说明系统是周期的。Lyapunov 指数谱所表现的系统动力学状态分布与分岔图基本一致。

在MATLAB 中设置时间步长为0.01，最大时长为2 000，新系统对于参数d 取不同值所得到的混沌吸引子相图如图4 所示。 由图可看出:当d ＝0.2 时，系统产生了一个双翼混沌吸引子；当d ＝0.8 时，系统产生了一个4 翼混沌吸引子；当d＝0.85 时，系统产生了一个6 翼混沌吸引子；当d＝1.02 时，系统产生了一个共存的双翼混沌吸引子。 该新系统在不同参数值下产生了不同的混沌吸引子，特别是在z 方向上分离产生了多翼吸引子，具有复杂的动力学行为。

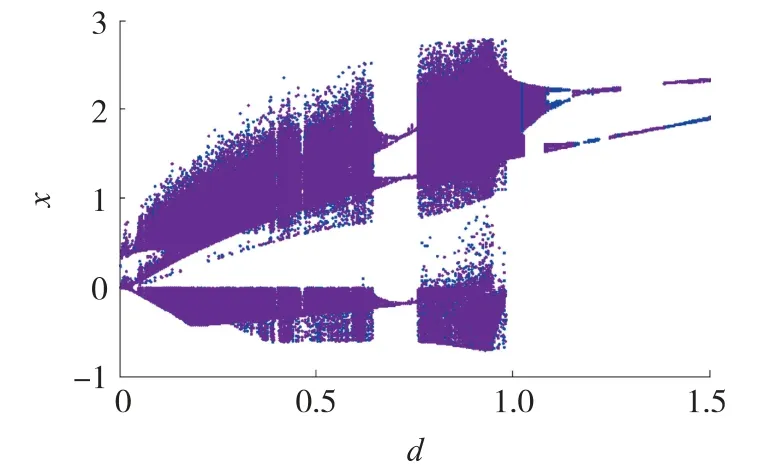
图2 参数d 分岔图

图3 参数d Lyapunov 指数谱

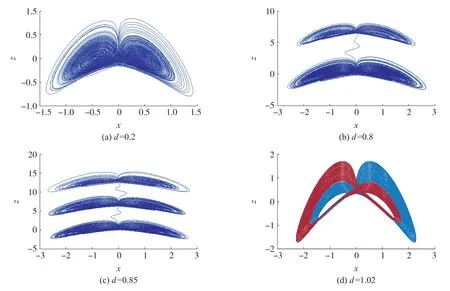
图4 新系统在不同d 值时混沌吸引子相图

2.4 初值对系统特性的影响

尽管混沌系统对变量的初始值具有高度敏感性，但大部分的系统在不同的初值下，运行轨迹最后都收敛到有限个吸引子上，而对于不同初始值导致系统运行轨迹收敛到无限个不同的吸引子上的现象被称为共存无限个吸引子现象，或称超多稳定性行为。

分析发现，当固定参数a ＝1，b ＝0.5，c ＝12 和d ＝0.3，初值x(0)＝2，y(0)＝2 保持不变，在不同的初值z(0)条件下，新系统(1)能够产生无限多种混沌吸引子共存现象，即新系统具有超多稳定性。 如图5 所示，当z(0)分别设置为-2π，0，2π，4π，6π，8π 时，对应的混沌吸引子分别为紫色，红色，绿色，黄色，浅蓝色和深蓝色吸引子。

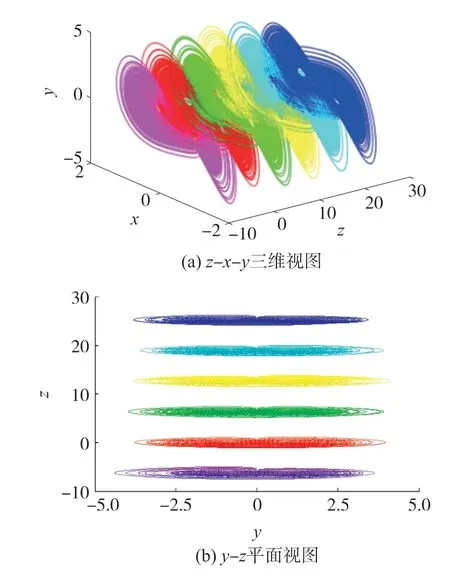
图5 初值z(0)影响下的共存混沌吸引子

保持系统参数不变，图6 给出了系统(1)随初值z(0)变化的分岔图。 由图6 可知，对于更多不同的z(0)值，系统(1)能够产生更多的共存混沌吸引子。 它进一步说明了新系统中无限多个混沌吸引子共存现象的客观存在性。 此外，如果设置参数a ＝1，b ＝0.5，c ＝12，d ＝1.2，同样取不同的初值z(0)为-2π，0，2π，4π，6π，8π，系统(1)能够产生无限多个共存周期吸引子，如图7 所示。

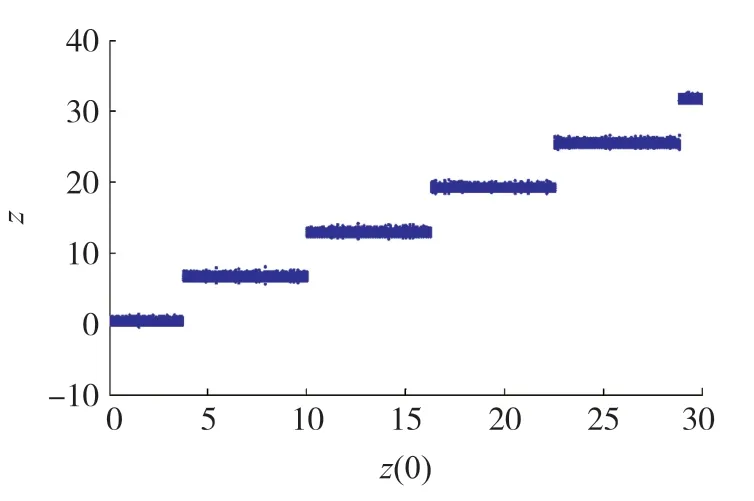
图6 系统随z(0)变化的分岔图

图7 初值z(0)影响下的共存周期吸引子

3 电路设计与仿真

混沌系统的电路实现对于实际工程应用具有根本的重要性[17-18]。 利用模拟运算放大器，模拟乘法器，正弦信号转变器以及电阻、电容对系统(1)进行电路设计与实现。 图8 给出了系统的电路图。 系统状态变量x，y，z 通过3 个积分器的输出电压表示。基于基尔荷夫电路定律，系统电路的等效电路方程为:

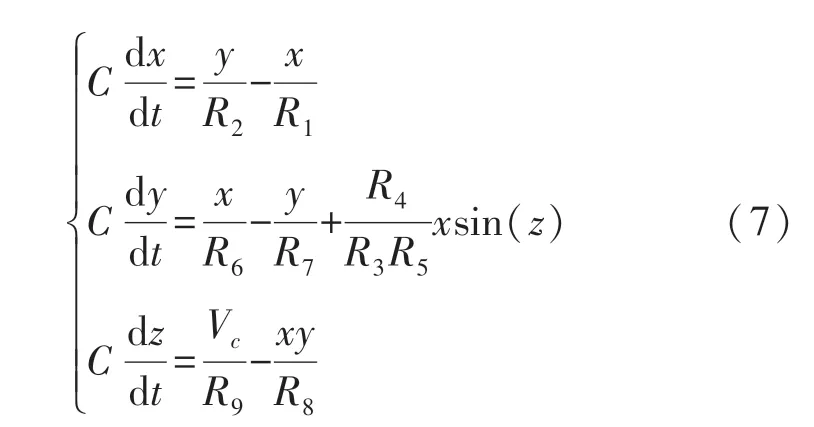
比较系统参数与电路元件，参数a ＝R/R1＝R/R2，b ＝R/R6＝R/R7，c＝R4/R3，d ＝Vc/R9。 在Multisim电路仿真软件中创建图8 所示电路，当a ＝1，b ＝0.5，c＝12 时，对应电路元件值设置为C ＝10 nF，R ＝10 kΩ，R1＝R2＝100 kΩ，R6＝R7＝200 kΩ，R5＝R9＝100 kΩ，R4＝10 kΩ，R3＝0.9 kΩ。 当d ＝0.3 和d ＝1.2 时，调节Vc值分别为0.33 V 和1.3 V，仿真结果分别如图9(a)和图9(b)所示。

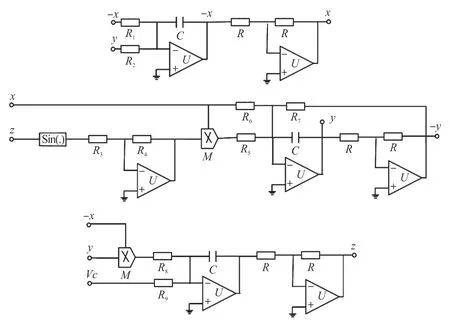
图8 系统电路原理图

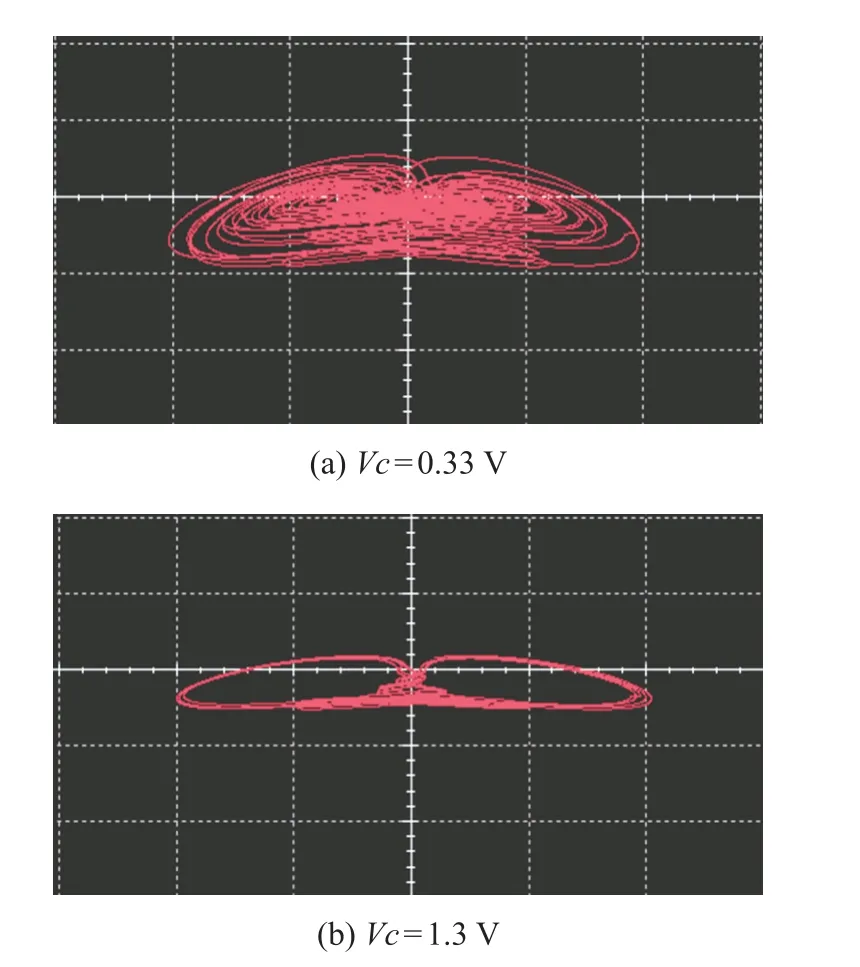
图9 Multisim 仿真结果

4 结论

本文针对一种具有无限多吸引子共存的三维连续混沌新系统，进行理论分析，MATLAB 数值计算和电路设计仿真研究。 研究结果表明，该系统在不同的系统参数下能够产生不同的多翼混沌吸引子，具有丰富的动力学特性。 特别是在固定系统参数下，通过改变初始值，该系统能够产生无限多吸引子共存的超多稳定性动力学行为。 通过设计模拟电路，用Multisim 得到新系统的一种混沌吸引子和一种周期吸引子，从而证实了系统的可实现性。 如此超多稳定性混沌系统，在保密通信中具有较高的应用价值。