无刷直流电机混沌系统时延估计控制
2021-03-23赵启亮骆万博储汇连
赵启亮,骆万博,李 慧*,秦 伟,储汇连
(1.长春工业大学 电气与电子工程学院,吉林 长春 130012;2.中国电建集团长春发电设备有限公司,吉林 长春 130012)
0 引 言
在工业生产以及制造过程中,无刷直流电机(Brushless Direct Current Motor,BLDCM)因其优良的工作性能正在逐渐成为很多执行机构的主要动力部件[1],并且它具有结构简单、运行效率高及调速性能好等优点,在工业自动化制造中引起了学者们的广泛关注。经研究发现,在某些特定的系统参数条件下,BLDCM存在混沌行为,主要表现为转矩间歇性波动、电机转速低频振荡,可严重破坏电机的稳定运行,甚至引起工业驱动系统崩溃[2]。因此,如何有效控制和抑制BLDCM的混沌行为成为当前研究的热点。
针对混沌系统的控制问题,研究人员都致力于提出有效的控制策略[3-9]。Li G等[6]提出了一种自适应神经网络反推控制法,利用神经网络作为通用逼近器估计未知的非线性函数,并根据分析李雅普诺夫稳定性原理及反步法实现了混沌同步控制;Alrifai M T等[7]采用一种鲁棒控制,即滑模控制(SMC),保证了系统状态与其期望值的收敛;Kocamaz U E等[8]对线性反馈、滑膜控制及无源控制进行对比得出,滑模控制具有较好的稳定性和实时性,线性反馈控制器虽然简单,但需要较大的控制增益,其控制性能优于无源控制器,但比滑模控制器差;Reza Ahrabi A等[9]基于T-S模糊模型,利用线性矩阵不等式(LMIS)设计了混沌卫星系统稳定与同步的预测控制器,实现了两个卫星系统的同步。然而,这些方法都存在一定的不足:反步控制和无源控制均取决于系统的数学模型,由于系统参数的不确定性,无法保证系统的动态性能;滑模控制要求系统参数不确定性满足特定的匹配条件,且控制器存在“抖振”现象;模糊控制通常基于系统的T-S不确定模糊模型,由于其计算量较大,响应速度较慢。
与上述方法相比,时延估计控制(Time-Delay Estimation, TDE)具有结构简单、易于调整参数、抗干扰能力强等优点,更容易应用于实际工程。为了控制BLDCM中的非期望混沌,文中采用基于时延估计法的BLDCM混沌控制法,该方法将参数不确定和外部干扰作为系统总扰动,通过时延估计器在线估计并补偿,使系统状态快速、稳定地到达期望平衡点。
1 BLDCM模型及动态特性分析
d-q坐标下的BLDCM状态方程为[10]
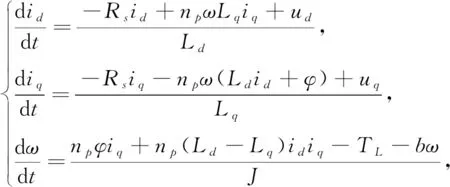
(1)
式中:id,iq----定子三相绕组在d-q空间坐标下的等效电流;
ud,uq----定子三相绕组在d-q空间坐标下的等效电压;
Ld,Lq----定子三相绕组在d-q空间坐标下的等效电感;
ω----转子角速度;
Rs----绕组电阻;
b----阻尼系数;
J----转动惯量;
φ----磁链系数;
np----磁极对数;
TL----负载转矩。
假设电机转子气隙磁场均匀,并对系统(1)进行线性映射与时间尺度变换[9],可得

(2)
式中:γ----自由参数;
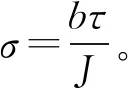
系统运行一段时间后,将系统的外部输入设置为零,即
此时相当于电机不受任何外力影响,电机数学模型为
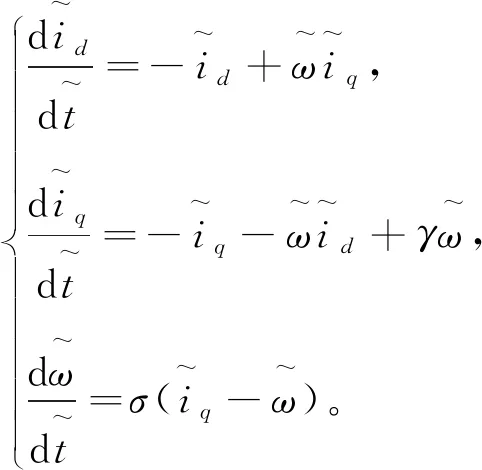
(3)
根据劳斯稳定判据可得[11],当


图的相轨迹曲线

图2 霍普夫分岔图
李雅普诺夫指数如图3所示。

图3 李雅普诺夫指数图
经计算,
LE1=0.414 7,
LE2=0.002 3,
LE3=-7.873 7,
Lyapunov维数
DL=2.052 4。
可见,系统最大Lyapunov指数为正,且为分数维。在该参数条件下,BLDCM处于混沌状态,因其非周期和不可预测性,会被认为是错误或故障而误处理,导致电机损毁,进而影响整个工程的运行。因此,有必要寻找有效的控制策略对BLDCM系统中存在的混沌行为进行控制。
2 BLDCM混沌系统的控制器设计
2.1 延时估计控制
令
那么含参数不确定及外部干扰的BLCDM模型为
(4)
式中:d1,d2----未知有界的外部干扰,‖d1‖≤ε1,‖d2‖≤ε2。

(5)
系统误差方程为
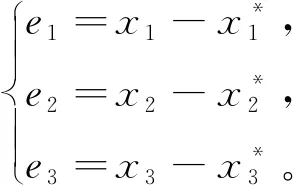
(6)
对误差方程(6)求导,可得
(7)
因此,只要使得误差e1和e2趋近于零,那么误差e3也将趋近于零。
误差系统(7)的前两个方程可表示为
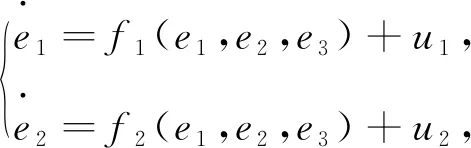
(8)
由于f1(e1,e2,e3)和f2(e1,e2,e3)是连续的,根据延时估计法,若τ足够小,那么
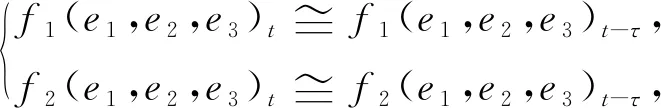
(9)
令

(10)
将式(8)代入式(10),可得

(11)

(12)
式中:k1>0,k2>0。
2.2 稳定性证明
若控制器满足式(12),则误差子系统(8)满足全局渐进稳定。
证明:
1)对于误差子系统(8),选取李雅普诺夫函数
对V求导,可得



(13)
式中:E1,E2----时延估计误差,其表达式为{E1=f1(e1,e2,e3)t-f1(e1,e2,e3)t-τ,
E2=f2(e1,e2,e3)t-f2(e1,e2,e3)t-τ。
(14)
当取集合
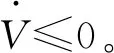
2)设误差e1和e2趋近于零的时间分别为t1和t2,那么当t≥max{t1,t2}时,误差e1和e2恒为零。此时可得误差系统(7)的第三个方程为
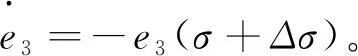
(15)
由于σ+Δσ>0,因此式(15)满足指数稳定。
综上所述,若控制器满足式(12),则误差系统(7)渐进稳定。证毕。
3 仿真分析
基于理论分析,通过MATLAB进行BLDCM混沌系统仿真实验。系统参数:
σ=5.46,
γ=17,
电机参数设定为:
L=14.25 mH,
R=0.9 Ω,
J=4.7×10-5kg·m2,
b=0.016 2 N·m/(rad·s-1),
那么系统的三个平衡点分别为P0(0,0,0),P1(16,4,4)和P2(16,-4,-4)。系统初始条件为
(x1,x2,x3)=(0.01,0.01,0.01),
外部扰动为
d1=d2=0.4sin(4πt),
采样时间为0.01 s,控制参数k1=70,k2=60,时延参数τ=0.001。
当5≤t<10时,系统期望平衡点为P1(16,4,4);当10≤t<15时,系统期望平衡点为P2(16,-4,-4)。
受控系统的相轨迹曲线如图4所示。
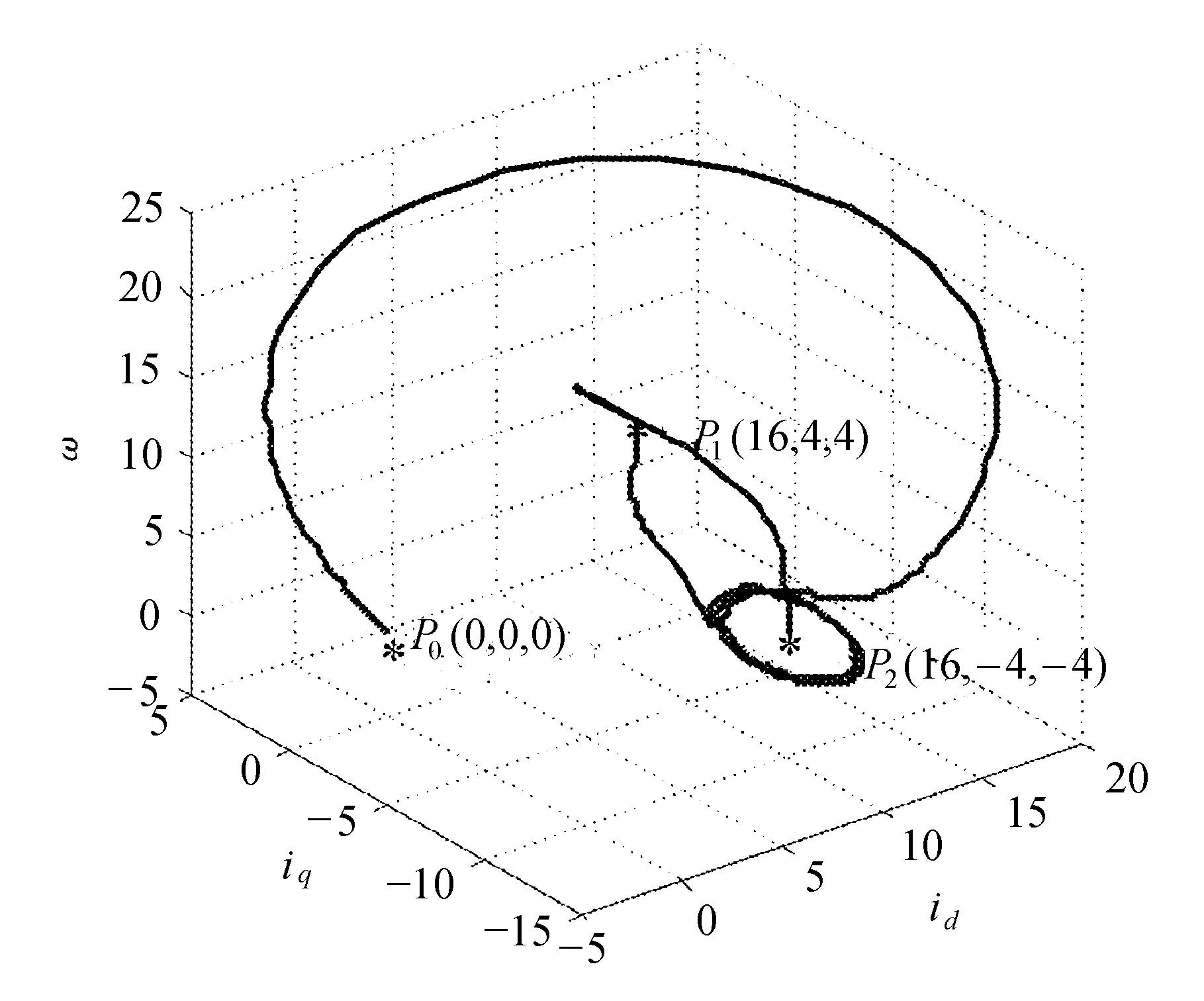
图4 受控系统的相轨迹曲线
受控系统的状态变量曲线如图5所示。

图5 受控系统的状态变量曲线
从图4和图5可以看出,在前5 s内,由于BLDCM系统未受控制,因此响应具有混沌现象;在5 s后加入时延估计控制器能够使系统在1~2 s内先后达到两个期望平衡点,从而有效地抑制了BLDCM混沌行为。
受控系统的状态误差曲线如图6所示。
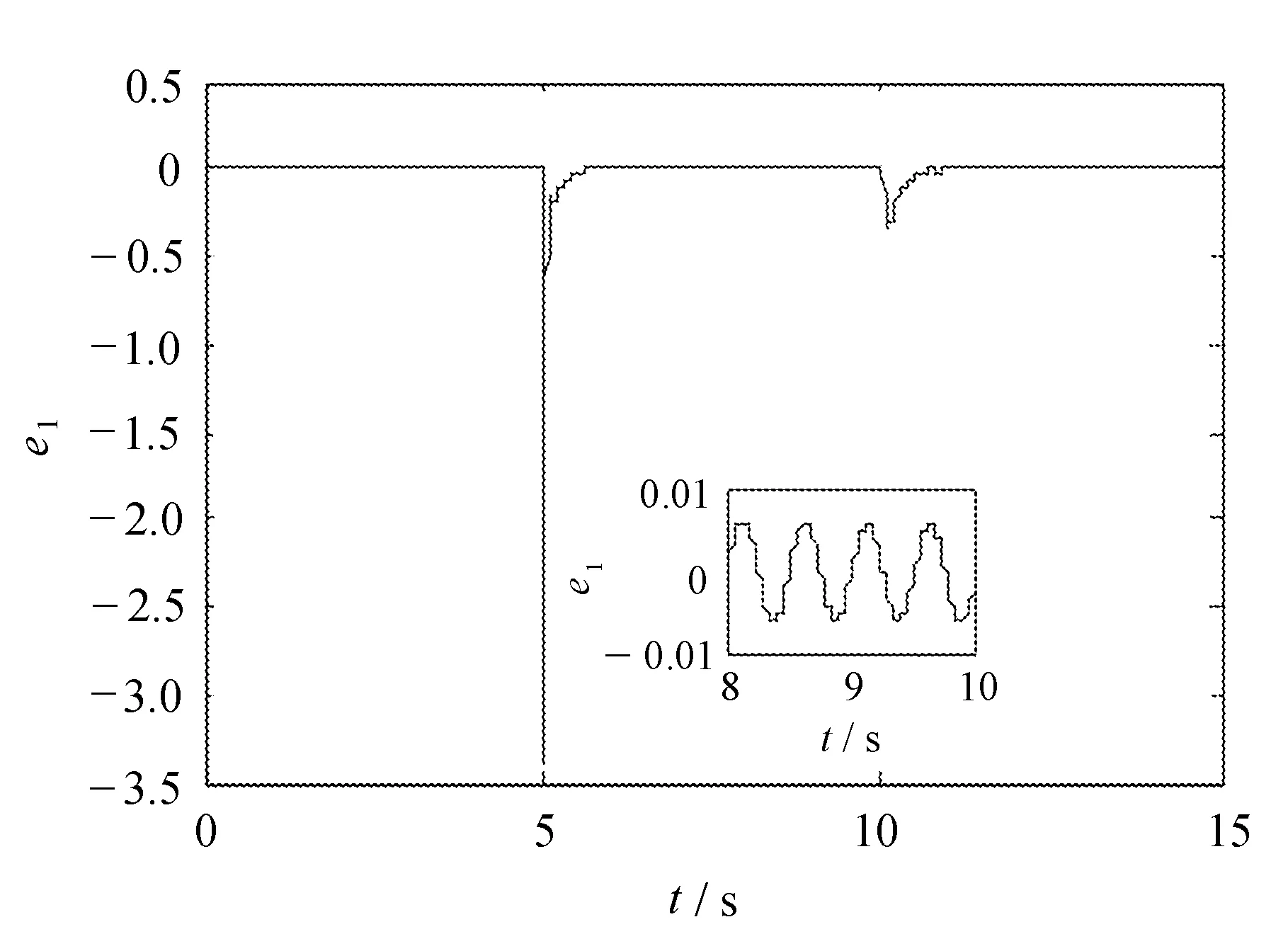
误差曲线
从图6可以看出,在加入控制器且系统相对稳定后,系统的3个状态量与平衡点的误差e1、e2和e3均小于0.01,因此受控系统的抗干扰能力强,即鲁棒性较好。
4 结 语
首先基于BLDCM的数学模型分析了混沌系统的动态特性,以及产生混沌现象的条件。其次,针对含有参数不确定及外部干扰的BLDCM混沌系统设计了时延估计控制器,并基于Lyapunov稳定性原理证明了系统全局渐进稳定。最后,通过仿真实验分析,时延估计法能够保证BLDCM的3个状态量在1~2 s内到达期望平衡点,且误差均小于0.01,从而验证了该方法的有效性和准确性。此外,该方法设计结构简单,易于调整参数,因此在工程上易于实现,对BLDCM的混沌控制具有一定的参考意义。
