基于gCoda方法的HMP成分数据分析

2021-03-23徐平峰牛彩虹王树达

长春工业大学学报 2021年1期

徐平峰，牛彩虹，孙萌，王树达

(长春工业大学数学与统计学院，吉林长春 130012)

0 引言

自然环境中微生物随处可见，在人体健康中扮演着重要角色。分析微生物群落间的关系可以探索微生物对我们生活环境的影响，而研究微生物的一个重要目标是推断微生物间的相互作用网络，这就涉及到了图模型。孙聚波等[1]在前人的基础上对图模型的基本概念进行了简要回顾。现有研究针对微生物的相互作用网络提出了几种方法;Friedman等[2]基于成分数据的对数比引入潜变量的概念，提出了Sparcc(Sparse Correlations for Compositional data)的近似方法来推断稀疏假设下的相关矩阵，但其没有考虑到成分数据中误差的影响，估计出的协方差矩阵也不能保证其正定性；Fang等[3]提出了CCLasso(Correlation inference for Compositional data through Lasso)，这种方法将加权最小二乘和l1惩罚结合起来推断相关矩阵，与Sparcc相比，其性能更好，但这些方法都没有统计假设可以保证能有效进行;Huaying Fang等[4]提出了一种新的惩罚最大似然方法gCoda(generation mechanism of compositional data)，从观察到的成分数据logistic正态分布推断微生物之间的稀疏直接相互作用网络，估计潜变量的逆协方差的稀疏结构。

文中采用gCoda方法分析HMP(NIH Human Microbiome Project)的数据，刻画人体中由基因组数据产生的成分数据的相关性，进而分析微生物相互间的作用关系，为研究微生物对人类健康和疾病等方面提供一些依据。

1 成分数据

Aitchison[5]首次提出对成分数据进行log-ratio变换，使得对成分数据的研究更进一步。假设y=(y1,y2,…,yp)T是p维随机计数潜变量，x=(x1,x2,…,xp)T能够被直接观测，且x与y的关系为

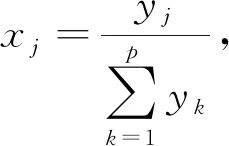
(1)

j=1,2,…,p,

lnx=lny-1plnw,

(2)

式中：1p----元素全为1的p维列向量。

2 gCoda

Fang H等[3]提出的gCoda方法中，假设成分数据服从logistic正态分布，可以将我们的推断转换为正态分布的逆协方差问题；假设相互作用网络是稀疏的，这可以解决由成分性引起的不确定性问题。

假设lny～Np(μ,Ω-1)，则(lnw,x)的联合密度分布为

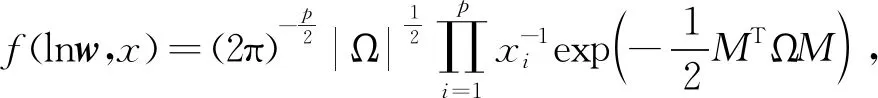
(3)

式中：M=lnx+1plnw-μ。

令变换矩阵

式中：Ep----p维单位矩阵。

对f(lnw,x)积分,得到f(x)的分布

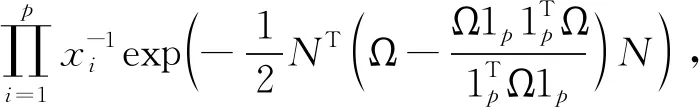
式中:N=F0lnx-F0μ。

样本X=(x1,x2,…,xp)是独立且同分布的，其负对数似然L(μ,Ω)为

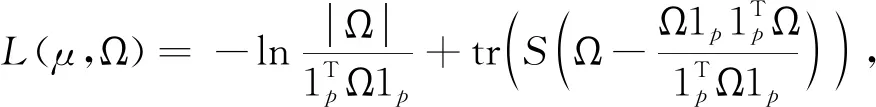
(4)

其中

假设E(F0lnx)的估计为E(F0μ)，得到Ω的负对数似然函数为

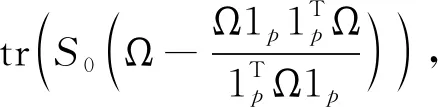
(5)

其中

处理稀疏协方差最常用的方法是给损失函数加一个惩罚项，所以用下面的函数作为我们的目标函数

f(Ω)=L(Ω)+λn‖Ω‖1,

(6)

其中

式中：λn----调节参数，λn>0。

gCoda的目的是找到惩罚似然的最大似然估计，即

(7)

由于式(7)是非凸的，所以用MM算法来迭代(Lange等[6])求解目标函数的最小值。当算法进行到第k步时，f(Ω)的替代函数为g(Ω)，即

gk(Ωk)=-ln|Ω|+tr(Ω(Ep-O)S0(Ep-P))+

λn‖Ω‖1,

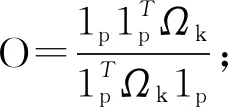
得出

gk(Ωk)=f(Ωk)。

gk(Ωk)可以被看做是一个标准的glasso问题，因为

tr(ΩSk)+λn‖Ω‖1,

(8)

其中

最终把MM算法的优化问题转化成通过坐标轴下降法可以解决的glasso[7]问题，同时用BIC(Bayesian Information Criterion)来选择惩罚参数。

3 数值模拟及实例分析

3.1 数值模拟

使用成分数据而非计数数据做如下模拟。考虑服从logistic正态分布的成分数据

X=(x1,x2,…,xp)，

其中:

xj=(x1j,x2j,…,xnj)T，

i=1,2,…,n，j=1,2,…,p，

lny～Np(μ,Ω-1)。

lny的均值向量μ从均匀分布[-0.5,0.5]p中产生,同时,用无标度图作为lny的协方差逆阵。

无标度图(Scale-free)使用B-A算法[8]建立一个无标度图。从单个顶点开始，然后一个接一个地添加p-1个顶点。每次新增一个节点时，新节点都与三个随机选择的旧节点相连，这些旧节点被选择的概率与当前图中每个节点的自由度有关。边缘强度在区间[-0.8,-0.6]和[0.6,0.8]的均匀分布中随机产生。为确保Ω是一个正定矩阵，我们把Ω的对角线元素都设置为5。

为评估gCoda的性能，将tpr(真阳性比率)、ppv(阳性预测率)和mcc(马修斯相关系数)作为评价指标。其中:

式中：tp，tn，fp，fn----分别为真阳性、真阴性、假阳性、假阴性的数量。

mcc的取值范围为[-1,1]，当得不到mcc的值时，将mcc的值记为-1。

设置变量个数p=50，样本量n=(100,200,500)，且对每个模型都进行50次模拟，计算tpr、ppv和mcc的值来评估gCoda的估计性能。

在不同样本量下，gCoda方法对无标度图进行估计，得到三个评价指标的均值与方差见表1。

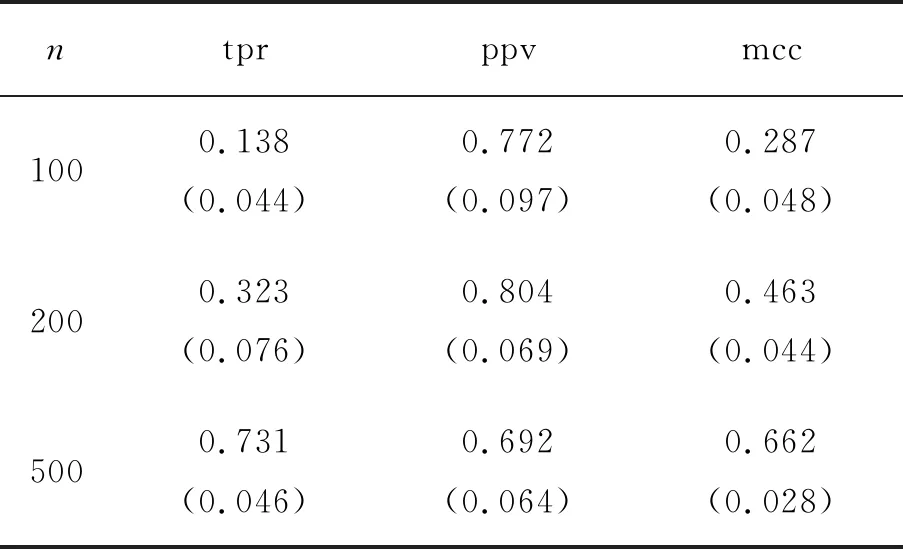
表1 不同样本量下，gCoda的性能(标准差)

由表1可以看出,随着样本量的增加，tpr和mcc的均值都在增加，即样本量越大,越可以估计得到更多的真边，估计所得到的图与真实图也越接近。

gCoda估计边数量的直方图如图1所示。

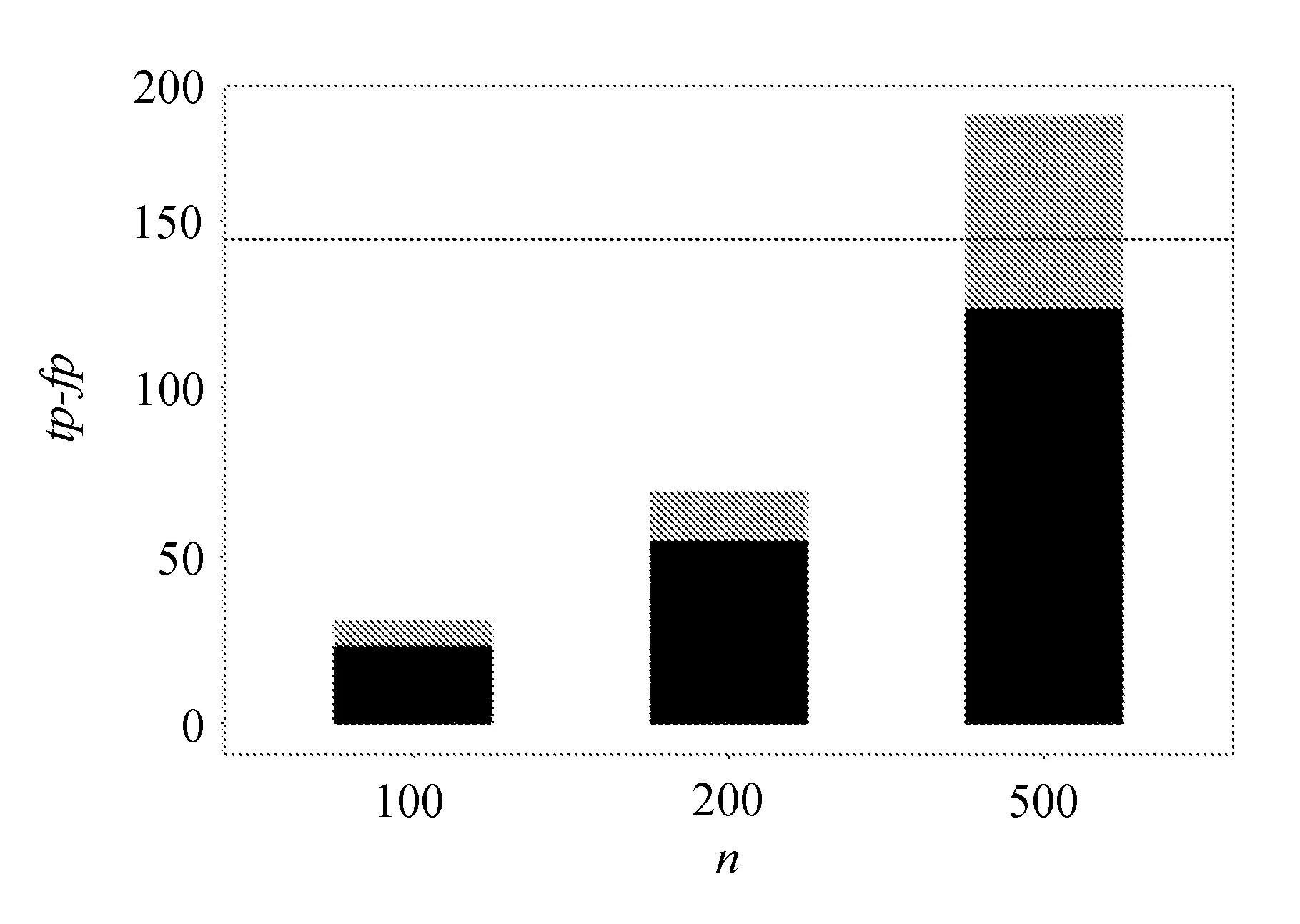
图1 gCoda估计边数量的直方图

图中，黑色代表tp的均值，灰色代表fp的均值，tp+fp是估计图中边的数量，而图中的横线表示原始图中存在边的数量。每幅图中横轴表示样本量的大小；纵轴代表tp+fp的数量。以上结果基于50次模拟得出的均值。

通过图1可以看到，随着样本量的增加，tp和fp的数量均增大，且当样本量为500时，tp的个数已经非常接近真实图中边的个数。

3.2 实证分析

OTUs是生物信息分析中一种常见的计数数据，文中所用OUT计数是不同人体的颊粘膜、喉咙等18个身体部位的样本。原始数据以及样本说明可以从网址http://hmpdacc.org/HMQCP/上获取。文中删除数据中OTUs为0的个数>60%的样本。值得注意的是，式(2)对成分数据进行对数运算，所以，文中对计数数据加了一个值为0.5的伪计数作为分析所用数据。除此之外，文中将分类不明确的OTUs剔除，并且按照每行、每列OTUs总计数不小于500筛选一部分样本，最终保留了2 744个样本，并选择其中60个变量进行数据分析。

用BIC准则选择得到的最优模型，如图2所示。

图2 gCoda估计图

由图2可以看到，编号54、10、22与其他所有变量都没有关系，而位于图中左下角的变量间具有复杂的相关性。同属细菌之间不仅具有相互关系，不同属细菌之间也可能存在关系，这可能与其生活环境有关。如编号11、12和44都是Bacteroides属，而编号34属于Ruminococcus属，编号48是Prevotella属，编号44与不同属的34、48具有相互关系，而与同属的11、12有关系。