一类参数曲线的积累平均弧长参数化方法*
2021-03-23贺诗涛申立勇
贺诗涛,申立勇
(中国科学院大学 数学科学学院,北京 100049)
*“第23届计算机辅助设计与图形学学术会议(CAD&CG 2020)”推荐论文.
计算机辅助几何设计(简称CAGD)[1]利用计算机强大的计算能力解决几何设计问题,研究自由型曲线曲面. 而找到既适合计算机处理,又能有效满足形状表示与几何设计要求,且便于形状信息传递和产品数据交换形状描述的数学方法,是CAGD的核心问题. 为清楚表达自由型曲线曲面,Ferguson[2]率先将参数多项式引入了CAGD. Schoenberg[3]提出了样条函数[4-5]用以解决连接问题,但曲线曲面形状控制的难题仍待解决. Bézier方法[6]更强调几何直观,并在解决整体形状控制方面有重大突破,但仍存在连接问题和局部修改问题. B样条方法[7-15]在保留Bézier方法优点的基础上成功解决了局部控制问题和参数连续性的连接问题,但在处理圆锥曲线和初等解析曲面时只能给出通常不合要求的近似表示. 为解决该问题,Forrest[16]先给出了有理Bézier形式的圆锥曲线,之后Versprille[17]提出了有理B样条方法. 非均匀有理B样条(简称NURBS)方法将有理与非有理Bézier曲线曲面、有理与非有理B样条相统一,不仅保留了非有理B样条的优点,还具有精确表达二次曲线曲面的功能. Sederberg等[18-19]提出了T样条方法,对B样条曲面进行了改进.
参数化在CAGD中具有重要作用. 设计者希望使用的参数化方法能尽量反应被插曲线或用数据点所构造曲线的性质. 此外,当给定控制顶点生成一条k次非均匀B样条曲线时,由于通常节点矢量未知,因此还需确定节点矢量中具体的节点值,同样要求参数化方法. 目前常用的参数化方法有均匀参数化、弦长参数化、向心参数化[20]和福利参数化. 本文提出积累平均弧长参数化法的一般框架,基于局部参数二次多项式插值和光顺性的约束准则,给出3种具体的积累平均弧长参数化法,并通过实例说明在给定约束准则进行局部插值后,其所赋予局部插值曲线的性质可从局部传递到整体,使得全局插值曲线在同一约束准则下的目标函数值小于弦长参数化和向心参数化的目标函数值.
1 理论框架
积累平均弧长参数化法可视为对弦长参数化的一个改进,将以直代曲的方法改进为以曲代曲,从而增加了一定的自由度,需要约束条件确定局部参数值. 约束条件不同使得积累平均弧长参数化法也不同. 这一特点使积累平均弧长参数化法灵活性较强,可根据实际需求自主选择相邻两点间曲线弧的构造方法,而目前已有的4种参数化方法都没有该特性. 一般地,对于平面上n个互异数据点Pi(xi,yi)(i=0,1,2,…,n),积累平均弧长参数化方法步骤如下:
1) 确定局部参数多项式插值曲线的次数m;
2) 选取合适的约束条件,以l个点为一组计算出数据点的局部参数和局部插值曲线在相邻两点间的弧长,即按P0,P1,…,Pl-1;P1,P2,…,Pl; …;Pn-l+1,Pn-l+2,…,Pn的顺序讨论,l由m和约束条件确定;
3) 根据局部插值曲线在相邻两点间弧长的平均值计算全局参数.
由上述步骤可知,当插值点较多时,该理论框架对应的问题是一个多参数非线性优化问题,一般方法求解该类问题的效率较低. 因此本文应用局部传递到整体的思路,给出一种基于局部求解,然后逐步积累弧长均值的方法. 先不断利用局部插值求出局部最优解,得到局部参数,然后将相邻两点间全部弧长的均值进行累积以求得全局参数,将此作为全局最优解的一个近似. 由实例计算可见,该近似解能使得全局插值曲线由约束条件决定的目标函数值小于传统参数化方法,如弦长参数化和向心参数化所对应的目标函数值,表明本文算法有效. 由于参数二次多项式曲线非常简单,因此本文给出的3种具体的积累平均弧长参数化法都基于局部参数二次多项式插值,区别在于约束条件的选取.
1.1 三点二次插值长度最短约束
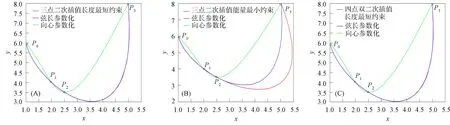
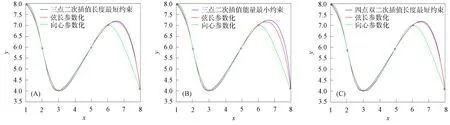
设平面上有3个互异数据点Pi(xi,yi)(i=0,1,2),过上述3点构造参数二次多项式插值曲线P,设其局部参数分别为0,u1,1,其中0 (1) 将式(1)写成分量形式为 (2) (3) 记 则可将式(2)和式(3)简化为 x=Au2+Bu+x0, (4) y=Cu2+Du+y0. (5) 由于u1是变量,当其取值在0~1区间变化时,二次参数多项式插值曲线P也会发生变化,因此为确定取值,需要一个约束. 在实际应用中,通常会遇到符合要求的曲线不唯一的情形. 为找到一条最符合要求的曲线,需给出一些约束准则. 考虑到波动剧烈的曲线通常相对较长,因此为选择波动小、更平直的曲线,可从曲线长度最短出发构造约束准则. 基于此,可令u1的取值使参数二次多项式插值曲线的目标函数值最小,目标函数为 为讨论方便,记被积函数为 (6) Q1=(2Au+B)2+(2Cu+D)2. 易见E1是以u1为自变量的一元函数. 求使E1达到最小的u1值,即为求E1的最小值点. 根据给定的约束准则,对Pi,Pi+1,Pi+2三点作局部参数二次插值并求出目标函数E后,可用如下算法计算: 步骤1) 在(0,1)上使用遗传算法(GA),求出最小值Emin; 步骤4) 若Eval1=Emin,Eval2>Emin,则ui+1=ua,并输出ui+1; 若Eval1>Emin,Eval2=Emin,则ui+1=ub,并输出ui+1; 若Eval1=Emin,Eval2=Emin,则: 最小值点的存在性可由物理背景说明,当最小值点不唯一时,可选取离估计值最近的一定精度的最小值点. 从而求得给定精度的最小值点,即u1的局部参数. 根据局部参数利用积累平均弧长参数化法求出其全局参数. 设Pi的全局参数为ti(i=0,1,2),则 t0=0,t1=t0+l1,t2=t1+l2, 其中l1,l2分别表示参数二次多项式插值曲线P在点P0与P1、P1与P2间的弧长,即 下面考虑平面上有4个数据点的情形. 设平面上有4个互异数据点Pi(xi,yi)(i=0,1,2,3),过点P0,P1,P2做参数二次多项式插值曲线Pa,记为Pa(xa,ya). 设P0,P1,P2的局部参数分别为0,u1,1,其中0 (7) 仿照三点情形求u1的值. 根据弧长公式分别计算Pa夹在P0和P1间的弧长l1及P1和P2间的弧长l21. 对于后三点,仿照前面的讨论重复操作. 过点P1,P2,P3做参数二次多项式插值曲线Pb,记为Pb(xb,yb). 设P1,P2,P3的局部参数分别为0,u2,1,其中0 (8) 易求出u2的值,从而Pb唯一确定. 根据弧长公式分别计算Pb夹在P1和P2间的弧长l22及P2和P3间的弧长l3. 下面根据数据点的局部参数求全局参数. 注意与三点情形相比的不同: 在数据点P1和P2间有两段参数二次曲线弧,它们通常并不重合,也不会有相等的弧长. 一种方法是舍去其中一段弧,只保留另一段弧,然后完全按照三点的情形计算全局参数,但这两段弧是用不全相同的3个数据点生成的,它们包含的数据点信息不全相同,如果舍去其中一段弧的弧长,则会浪费一个数据点的信息. 另一种方法是在局部插值过程中,避免相邻两点间出现两段弧,如假设平面上有5个数据点,令Pa插值于数据点P0,P1,P2,而Pb插值于数据点P2,P3,P4,这样相邻两点间总只有一段参数二次曲线弧,但这种方法对数据点的数量有一定要求,只有在数据点个数可表达成2n+3的形式时才能使用,使得该方法有较大的局限性. 因此,需找到一种更合适的方法能同时使用l21和l22,从而不会发生信息丢失的问题,也不会因为数据点的个数问题产生局限性. 最简单的方法是用l21和l22的算术平均值代替其中某一段弧的长度,从而可得计算数据点全局参数的公式为 (9) 最后考虑平面上(n+1)个数据点的情形,其中n>3,这种情形的做法和四点情形完全相同. 设平面上有(n+1)个互异数据点Pi(xi,yi)(i=0,1,2,…,n). 首先仿照上述方法,利用长度最短的约束准则计算插值于P0,P1,P2的参数二次多项式曲线,并分别计算夹在P0和P1间的弧长l1及P1和P2间的弧长l21;然后对下面的3个相邻数据点进行相同操作,分别计算夹在P1和P2间的弧长l22及P2和P3间的弧长l3. 以此类推,以相邻3个数据点为一组,利用长度最短的约束准则计算插值于Pi,Pi+1,Pi+2的参数二次多项式曲线,并分别计算夹在Pi和Pi+1间的弧长li+1,2及Pi+1和Pi+2间的弧长li+2,1,其中i=2,3,…,n-1. 最后利用积累平均弧长的方法计算数据点的全局参数,公式为 (10) 下面给出以能量最小作为约束准则的方法,其来源于样条的应变能. 在仅改变约束准则的条件下,积累平均弧长参数化法的步骤几乎与三点二次插值长度最短约束方法完全一致,因此这里只考虑四点情形. 设平面上有4个互异的数据点Pi(xi,yi)(i=0,1,2,3),过点P0,P1,P2做参数二次多项式插值曲线Pa,记为Pa(xa,ya). 设P0,P1,P2的局部参数分别为0,u1,1,其中0 使用能量最小约束准则,令u1的取值使得插值于P0,P1,P2的参数二次多项式插值曲线能量最小,从而求得唯一的插值曲线Pa,目标函数为 其中ka是插值曲线Pa的曲率,ds是弧微分. 将目标函数写为 根据曲率公式和弧微分公式,可计算得到Q1的表达式为 采用数值积分方法计算E1,然后根据三点二次插值长度最短约束算法计算u1的值. 从而分别计算出Pa夹在P0和P1间的弧长l1及P1和P2间的弧长l21. 对于P1,P2,P3,可类似求出满足约束准则的u2值,然后根据弧长公式分别计算出Pb夹在P1和P2间的弧长l22及P2和P3间的弧长l3. 于是可得计算数据点全局参数的公式为式(9). 首先考虑四点的情形. 设平面上有4个互异数据点Pi(xi,yi)(i=0,1,2,3),过点P0,P1,P2做参数二次多项式插值曲线Pa. 设P0,P1,P2的局部参数分别为0,u1,1,且满足0 过点P0,P1,P2做参数二次多项式插值曲线Pb. 设P1,P2,P3的局部参数分别为0,u2,1,且满足0 (11) 由于式(11)等号右边的两个积分都是非负的,因此可知E取最小值时,这两个积分分别取最小值. 利用三点二次插值长度最短约束算法分别求出u1和u2的值,即可根据积累平均弧长计算全局参数. 当数据点增多时,可以相邻四点为一组进行类似讨论. 例如,当数据点数为5时,可仿照上述方法得到全局参数的计算公式为 (12) 针对6个及以上互异点的全局参数计算公式为 (13) 与三点二次插值方法相比,四点双二次插值改变了相邻两点间局部插值曲线段的数量,从而在表达式上呈现出加权平均的形式,即得到了与三点二次插值方法不同的全局参数. (A) 弦长参数化,向心参数化,三点二次插值长度最短约束; (B) 弦长参数化,向心参数化,三点二次插值能量最小约束;(C) 弦长参数化,向心参数化,四点双二次插值长度最短约束.图1 例1中点在不同参数化和约束条件下的多项式插值曲线Fig.1 Polynomial interpolation curves of points in example 1 under different parameterizations and constraints 下面通过实例计算将上述3种具体的积累平均弧长参数化法与弦长参数化法、向心参数化法进行比较,以说明新参数化方法的优势. 例1设平面上有4个数据点:P0(1,6),P1(2,4),P2(2.5,3.5),P3(5,8). 做插值于这4个点的参数多项式曲线,结果如图1所示. 由图1可见,长度最短约束的积累平均弧长参数化曲线与弦长参数化曲线相近. 长度最短约束的目标函数并非弧长公式,从而导致虽然向心参数化的曲线弧长最短,但在此约束准则下目标函数值最大. 在给定约束准则进行局部插值后,其赋予局部插值曲线的性质可从局部传递到整体,使得全局插值曲线在同一约束准则下的目标函数值小于弦长参数化和向心参数化的目标函数值,对比结果如下:对例1中的点分别进行弦长参数化、向心参数化及三点二次插值长度最短约束下的积累平均弧长参数化法所得长度最短约束目标函数值分别为14.352,20.144,13.997;对例1中的点分别进行弦长参数化、向心参数化及三点二次插值能量最小约束下的积累平均弧长参数化法所得能量最小约束目标函数值分别为1.738,3.922,1.616;对例1中的点分别进行弦长参数化、向心参数化及四点双二次插值长度最短约束下的积累平均弧长参数化法所得长度最短约束目标函数值分别为14.352,20.144,13.997. 由上述对比结果可见,约束准则所赋予的局部性质确实从局部传递到了全局插值曲线,在该约束准则下计算出的全局插值曲线的目标函数值与弦长参数化和向心参数化相比有明显降低. 例2根据如下有序数据点集做参数三次样条插值曲线: {(1,8),(2,6),(3,4),(5,6),(6,7),(8,4)},结果如图2所示,图2中“∘”表示数据点. (A) 弦长参数化,向心参数化,三点二次插值长度最短约束; (B) 弦长参数化,向心参数化,三点二次插值能量最小约束;(C) 弦长参数化,向心参数化,四点双二次插值长度最短约束.图2 例2中点在不同参数化和约束条件下的多项式插值曲线Fig.2 Polynomial interpolation curves of points in example 2 under different parameterizations and constraints 由图2可见,目标函数值小的性质仍可由局部传递到整体,对比结果如下:对例2中的点分别进行弦长参数化、向心参数化及三点二次插值长度最短约束下积累平均弧长参数化法所得长度最短约束目标函数值分别为15.704,23.929,7.821;对例2中的点分别进行弦长参数化、向心参数化及三点二次插值能量最小约束下的积累平均弧长参数化法所得能量最小约束目标函数值分别为7.085,50.689,5.932;对例2中的点分别进行弦长参数化、向心参数化及四点双二次插值长度最短约束下积累平均弧长参数化法所得长度最短约束目标函数值分别为15.704,23.929,8.763. 例3根据如下有序数据点集做参数三次样条插值曲线: {(0,10),(2,10),(3,10),(5,10),(6,10),(8,10),(9,10.5),(11,15),(12,50),(14,60),(15,85)},结果如图3所示,图3中“∘”表示数据点. (A) 弦长参数化,向心参数化,三点二次插值长度最短约束; (B) 弦长参数化,向心参数化,三点二次插值能量最小约束;(C) 弦长参数化,向心参数化,四点双二次插值长度最短约束.图3 例3中点在不同参数化和约束条件下的多项式插值曲线Fig.3 Polynomial interpolation curves of points in example 3 under different parameterizations and constraints 由图3可见,3种积累平均弧长参数化法生成的插值曲线都与弦长参数化法生成的插值曲线几乎重合,但目标函数值却有较大差异,对比结果如下:对例3中的点分别进行弦长参数化、向心参数化及三点二次插值长度最短约束下的积累平均弧长参数化法所得长度最短约束目标函数值分别为85.479,419.640,26.606;对例3中的点分别进行弦长参数化、向心参数化及三点二次插值能量最小约束下的积累平均弧长参数化法所得能量最小约束目标函数值分别为3 915.396,1 166.199,42.341;对例3中的点分别进行弦长参数化、向心参数化及四点双二次插值长度最短约束下的积累平均弧长参数化法所得长度最短约束目标函数值分别为的85.479,419.640,26.607. 与传统的参数化方法相比,积累平均弧长参数化法通过局部二次插值引入了额外的自由度,可利用约束准则或其他方法赋予局部插值曲线某种性质,从而使局部插值曲线的性质传递到全局插值曲线上. 这种方法可以使设计者根据需求设计参数化方法,并得到具有所需性质的全局插值曲线. 而无论是弦长参数化还是向心参数化方法均无主动设计的空间,其忽略了不同研究者对插值曲线的性质可能有不同的需求,而自身又无法保证能生成最优的曲线. 本文方法给出了一种解决该问题的思路,但本文目标只把一个性质从局部传递到整体而非多个,因此求得的并非全局最优解,而为其一个近似解,该近似解能达到全局插值曲线的目标函数值小于弦长参数化和向心参数化结果的目标. 图4 质点从P0到P3路径示意图Fig.4 Schematic diagram of particle’sroutes from P0 to P3 设平面上有4个数据点,质点从P0出发,依次经过P1,P2,最终到达P3. 将数据点的全局参数视为质点从P0运动到Pi所经过的路程. 此时问题转化为求质点从Pi运动到Pi+1的路程. 图4为质点从P0到P3路径示意图. 由图4可见,平面上存在4个互异数据点及一个直角坐标系. 在具体问题中需明确坐标系和数据点的坐标,这里为便于说明,只给出其示意图,不考虑点在给定坐标系中的具体坐标. 首先,考虑质点从P0运动到P1的路程. 由于质点的实际运动路径未知,所以需构造一条连接P0和P1的特殊路径,并用其长度对实际路程进行近似. 弦长参数化中用连接P0和P1线段的长度进行近似,该方法简单,但实际上质点不能恰好做直线运动,所以误差相对较大. 考虑用参数二次曲线弧的长度对实际路程进行近似,这种方法不会带来高次插值的问题及过大的计算量,同时也能体现路径的弯曲. 注意到质点在到达点P1后将会经过点P2,因此可考虑利用P2构造一条从P0到P1的参数二次多项式曲线弧,并做出某种限制使该弧唯一,即得到了所需的特殊路径,如图4中红色曲线所示. 对于质点从P0运动到P1,质点经过P2这一事件发生于未来,因此本文用质点从P0运动到P1这一段运动的未来信息构造质点从P0运动到P1的一条特殊路径以及相应的路程. 考虑质点从P1运动到P2的路程. 注意到质点在经过P2后将会到达P3,从而可利用数据点P3,即质点从P1运动到P2这段运动的未来信息构造一条特殊路径,如图4中绿色曲线所示. 质点在到达P1前曾经过P0,可利用数据点P0,即质点从P1运动到P2的这段运动的过去信息构造一条特殊路径,如图4中红色曲线所示. 本文可进一步认为局部参数值之间有关联,即质点的过去运动状态和未来运动状态有关联. 这种思路可用于四点双二次插值的积累平均弧长参数化法. 于是得到了从P1到P2的两条特殊路径. 本文可要求质点沿红色或绿色的曲线运动,用这段曲线的弧长对P1到P2的实际路程进行近似. 该方法会丢失一个数据点的信息. 从物理角度看,这样做会丢失质点运动状态的信息. 为对质点的实际运动路程做更精确的近似,需要更多质点运动状态的信息. 考虑如下问题: 假设有大量质点从P0出发运动到P1,则有些质点可能会沿红色路径运动到P2,而其他质点会沿绿色路径运动到P2. 即质点从P1运动到P2所选择的路径是一个随机现象,其样本空间元素个数为2. 而质点从P1运动到P2的路程可视为一个随机变量,该变量为离散随机变量,因此可从概率论的角度考虑问题. 当质点选择红色、绿色路径的概率已知时,则可根据两种颜色的曲线夹在P1,P2间的弧长计算出质点从P1运动到P2的路程的期望,将其作为质点从P1运动到P2的实际路程的近似值. 上述分析表明,这两条路径的重要程度对质点是相同的,质点选择两条路径中任意一条的概率均为1/2. 于是可计算出质点从P1运动到P2的路程的期望等于两段弧长的算术平均值. 若质点选择两条路径中任意一条的概率不相等,例如,质点沿路程长的路径运动的概率小,或质点沿能量大的路径运动的概率小. 则此时从表达式上看,应对相邻两点间的全体曲线弧的长度计算加权平均,而非算术平均. 质点从P2运动到P3的讨论类似于从P0运动到P1,差异在于后者以P0为起点,在其之前并无数据点,即无法使用质点过去运动状态的信息; 前者以P3为终点,在其后无数据点,即无法使用质点未来运动状态的信息. 从物理的角度看,这3种方法在思想上没有本质区别,针对于不同的需求提出不同的约束需求,例如,数控机床(CNC)轨迹规划中在本文的能量最小约束下可具有更好的加工进给速度. 此外,对于其他数据点个数的情形,物理解释也相同. 对于计算不位于两端的数据点的全局参数,关键是首先构造多条特殊路径,然后计算弧长平均值或路程期望,用其对实际弧长或路程进行近似. 综上所述,本文给出的3种积累平均弧长参数化方法都按积累平均弧长参数化法的一般框架给出,无论是参数多项式插值还是参数三次样条插值,均可得到在所选约束准则下比弦长参数化和向心参数化目标函数值更小的结果. 本文只对低次参数多项式插值和参数三次样条插值在不同参数化方法下求得的目标函数值进行了对比. 本文给出的参数化方法虽在算例中可使目标函数值小于弦长参数化和向心参数化的结果,但也存在一些示例使得积累平均弧长参数化法计算得到的目标函数值大于弦长参数化或向心参数化的结果. 对这些示例进行计算表明,积累平均弧长参数化给出的全局参数较接近弦长参数化给出的参数,并且由于前者给出的全局参数总不小于后者在对应点给出的参数,使得前者得到的全局参数可被视为对后者的一个参数增加的扰动. 若积累平均弧长参数化给出的目标函数值与几种方法中目标函数最小值相差较小,则可从数值误差方面进行分析.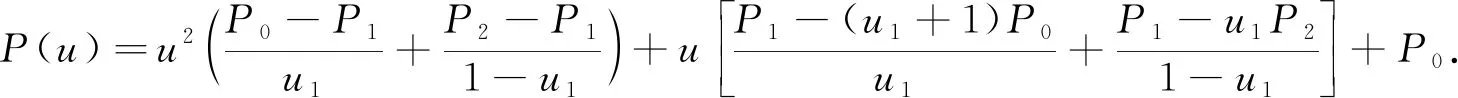
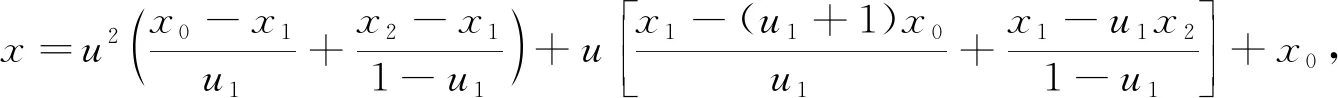
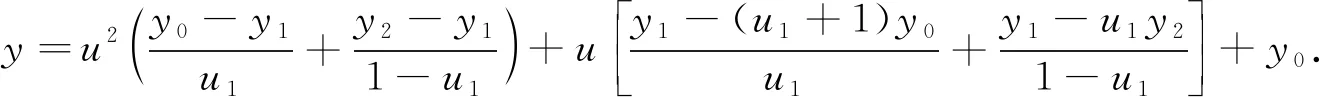
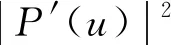
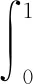
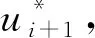

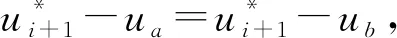
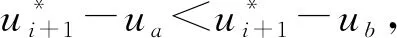
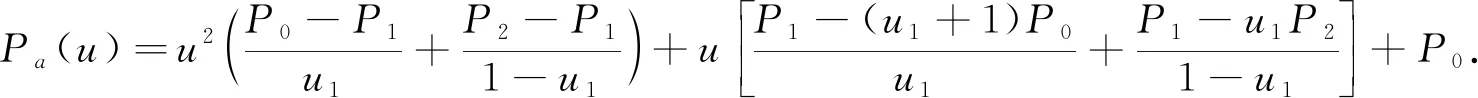
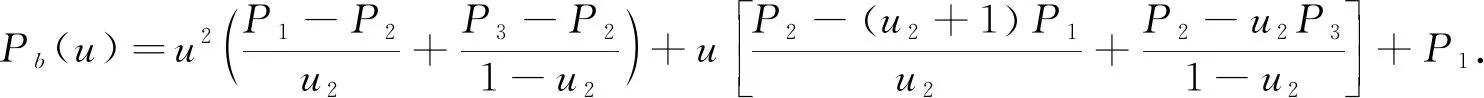
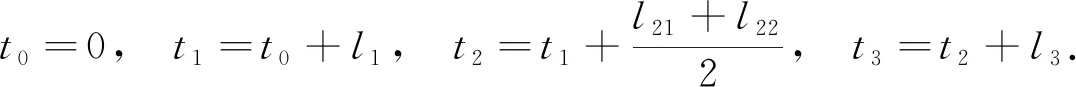
1.2 三点二次插值能量最小约束
1.3 四点双二次插值长度最短约束
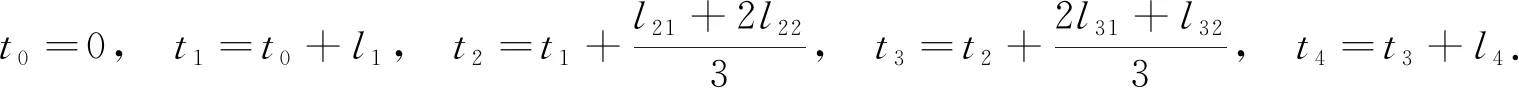
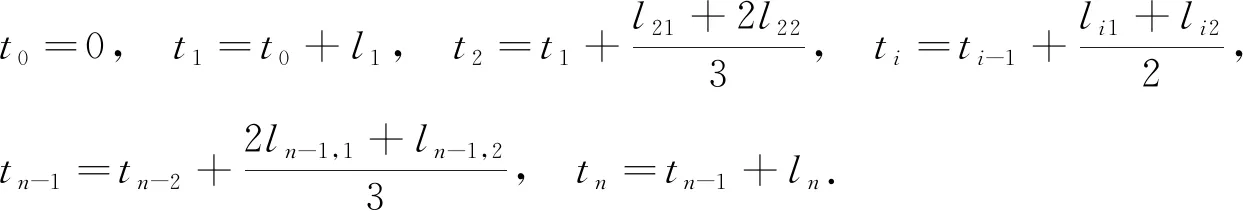
2 实例计算

3 物理解释