模板引导与数据驱动的三维碎骨修复方法*
2021-03-23蒋俊锋孙晓莉邓子越何坤金陈正鸣刘宏伟张文玺
蒋俊锋,孙晓莉,邓子越,黄 瑞,何坤金,陈正鸣,刘宏伟,张文玺
(1. 河海大学 物联网工程学院,江苏 常州 213022; 2. 河海大学 计算机与信息学院,南京 210024; 3. 南京医科大学附属常州第二人民医院,江苏 常州 213003; 4. 溧阳市人民医院,江苏 溧阳 213300)
0 引 言
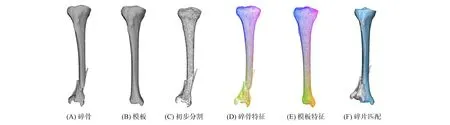
面向骨折修复的计算机辅助术前规划中,需要先分割三维碎骨再修复碎骨[1-2],如图1所示. 这种处理方法通常费时费力,原因如下: 1) 骨折形态随机,碎骨会发生相互接触;2) 断裂边界的曲率有时不显著;3) 碎骨拼接时,对于细小碎骨通常可以丢弃;4) 骨骼不仅包含相对光滑的外表面,还包含形态复杂的内部松质骨. 目前已有的软件自动化程度较低,相关方法不能较好地支持这种随机断裂的碎骨分割和拼接.
本文考虑对输入的碎骨三角网格模型,提取碎骨外表面,并在骨骼断裂和碎骨块接触边界对碎骨进行分割,然后以每个碎骨外表面为单元进行碎骨拼接,完成骨折高效修复,从而有效提高骨折修复术前规划的自动化程度和效率. 研究表明,碎骨分割与拼接两者相辅相成,将对侧健康骨模型作为先验模板,能有效提高分割和拼接的正确率. 基于此,本文提出一种基于模板与数据驱动的三维碎骨分割与拼接方法,通过模板匹配、特征深度学习等方法,实现分割-拼接迭代求精.
1 相关工作
碎骨修复主要涉及碎骨形状分割和拼接两方面内容. 碎骨分割包含提取骨骼外表面及将相互接触的碎骨分隔开; 碎骨分割后,需要通过刚体变换对碎骨调整位置进行拼接.
1.1 形状分割
三维模型分割的目标是将模型分割成互不相交的部分. 若需对各分割部分进行语义标记,则这种分割称为语义分割. 经典三维分割方法来源于二维图像分割,主要包括区域增长、分水岭、迭代聚类、层次聚类和边缘分割等方法[3]. 区域增长法是一种交互式算法,效率较高,但存在种子点和增长停止条件不易选择的问题; 分水岭算法存在分割边界锯齿形状、过分割等问题,通常需要边界光滑和分割区域合并等后处理操作; 迭代聚类需预先指定分割数量,对于三维模型的初始分割较敏感; 层次聚类是一种多分辨率的聚类分割方法; 基于边缘分割方法试图找到分割边缘,但边缘常不易封闭.
近年来,基于数据驱动的三维形状分割研究备受关注. 根据有无训练数据,可将分割方法分为有监督学习[4-9]和无监督学习[10-11]. 根据三维形状表示方式,三维形状分割可分为基于多视图[4]、点云[5-6]、图[7]、网格[8]和体素[9]等方法. 其中,多视图方法利用传统的二维图像卷积神经网络,基于点云、图、网格、体素的神经网络方法分别研究对应表示方式的卷积、池化等操作; 此外,还有一种方式是先手工提取网格模型特征,然后以网格模型特征为神经网络的输入,通过卷积、池化操作进一步提炼分割特征[12-13]. 现有数据驱动方法通常先利用神经网络训练(有监督)或聚类(无监督)进行初步分割,再利用图割法等传统方法修正边界,其中,利用神经网络或聚类的标签概率作为图割法目标函数的约束项. Zhou等[14]先训练两个神经网络,用于初步分割网格及其标记边界,然后利用图割法结合边界引导进一步实现有效分割;Xu等[13]提出了一种三维牙齿模型分割方法,先用训练的两个神经网络分别对牙齿和牙龈以及牙齿之间作语义分割,然后利用图割、主成分分析等方法修正分割结果;Shu等[10]利用一种无监督学习的三维形状分割方法,先通过自编码器提取特征,然后对特征用高斯混合模型进行分割,最后用图割法修正分割.
三维骨骼模型的分割方法,通常利用模板对骨骼进行分割[15-16]. 本文提出一种基于模板分割健康骨骼的方法[17]. 该方法在提取少量特征点的基础上,先对骨骼网格模型进行语义分割,然后对分割得到的模板,基于Laplace变形进行非刚体配准,从而指导同类骨骼模型实现快速兼容性分割.
对于碎骨分割,Shadid等[18]提出了一种基于随机分水岭变换的方法实现了踝部碎骨CT图像分割. 目前,面向三维碎骨分割的研究尚未见文献报道. 经CT三维重建后,三维骨骼模型内部包含形态复杂的内部组织,如图1所示,碎骨相互接触的边界形态随机复杂,同时,分割过程还需去除细小碎骨. 因此,利用目前已有方法提取外表面并同时进行精准碎骨分割十分困难.
1.2 碎片拼接
碎骨复位属于碎片拼接范畴,主要用于文物复原[19]和碎骨复位[20-25]. 按照碎片数量,碎片拼接可分为一对一拼接和多对多拼接两类. 多对多拼接研究[23,26-27]着重于两个以上碎片拼接,碎片全局拼接是一个带约束的非线性组合优化问题. 当碎骨数量较多时,搜索空间较大,搜索效率较低. 目前的全局拼接搜索方法包含贪心法[19]、分支限界法[28]等. 其中,基于图的贪心搜索方法效果较好,但有时很难找到全局最优解,尤其在缺失碎片数量较多时,贪心搜索方法易产生错误拼接. 一对一拼接研究[28-29]常用方法包括四点配准法[30]、相关法[23]、随机一致性采样[22]等,其中四点配准法效率较高. 按照断裂边界不同可分为基于断裂线的复位[21,27]和基于断裂面的复位[19,23]. 目前的方法多数依据断裂面曲率变化特性识别断裂面,以断裂面或断裂面的子区域为拼接单元,对拼接单元进行刚体配准. 按照是否利用模板,碎片拼接可分为有模板拼接[21-24]和无模板拼接[25,31-33]两种. 对位对线的粗隆间骨折碎骨复位方法[33]属于无模板拼接,该方法较好解决了包含骨骼轴线成角约束的骨骼拼接问题,为临床粗隆间骨折复位术前规划提高了自动化程度. 有模板拼接通常利用对侧健康骨骼[21-24]或形状统计模型[34]作为模板,其关键是构建碎骨外表面与模板的对应关系,尤其当碎骨面积较小或者碎骨外表面特征不显著时,对应关系计算较难实现.
2 方法概述
本文方法总体流程如图2所示,输入为包含内部组织且未分割的三维碎骨模型,以及该碎骨模型的对侧健康完整骨骼,输出为分割且拼接好的碎骨外表面集合. 总体采用分割-拼接迭代求精的思想实现碎骨分割和拼接.

图2 方法总体流程Fig.2 Overall process of method
1) 碎骨分割: 由于人体骨骼外表面较相似,具有统计学特征,骨骼断裂面和骨骼松质骨形态较复杂,因此,本文考虑通过训练神经网络初步提取碎骨外表面; 然后通过碎骨与模板匹配后,用模板与碎骨表面之间距离差异以及碎骨顶点的曲率变化信息作为判据,进一步确定外表面边界.
2) 碎骨拼接: 先将碎骨刚体配准到模板,模板匹配关键问题在于构建碎骨到模板之间的密集对应关系,本文通过训练神经网络回归学习骨骼的表面特征; 然后将所有初步提取的碎骨外表面整体作为神经网络输入,预测每个碎片的表面特征,同时预测模板的表面特征,通过特征匹配构建碎片与模板的对应关系,完成碎骨碎片与模板对齐; 最后用ICP(iterative closest point)[35]方法修正对齐结果; 在每次迭代过程中需重新计算碎骨碎片特征,可通过标签传递将对侧骨模板特征映射到碎骨碎片.
3) 分割与拼接迭代求精: 碎骨分割、碎骨表面特征计算、碎骨拼接这三者相互依赖、相辅相成. 拼接结果越好,碎片整体越接近于一个健康骨骼的形态,使碎骨表面的特征回归精准度更高,促进模板匹配的精度,从而进一步提高分割和拼接精度. 因此本文考虑三者不断迭代,逐步求精.
本文算法步骤如下:
输入: 输入模型为碎骨模型M和健康对侧骨模型N(M为碎骨模型点云矩阵,N为对侧骨模型点云矩阵),最大迭代次数P,收敛阈值δ;
输出: 修复的碎骨模型{RiMi+ti},Mi⊆M,Mi∩Mj=Ø,其中Mi为第i个碎骨点云矩阵,Ri和ti分别为第i个碎骨旋转变换矩阵和平移变换矩阵;
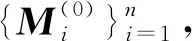
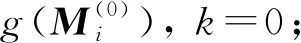
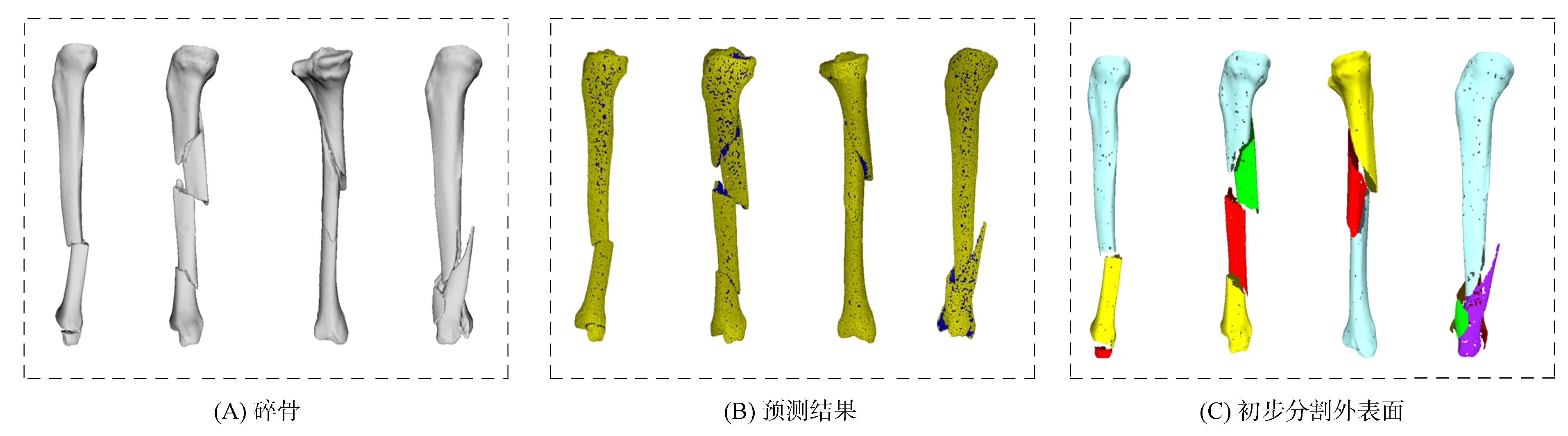
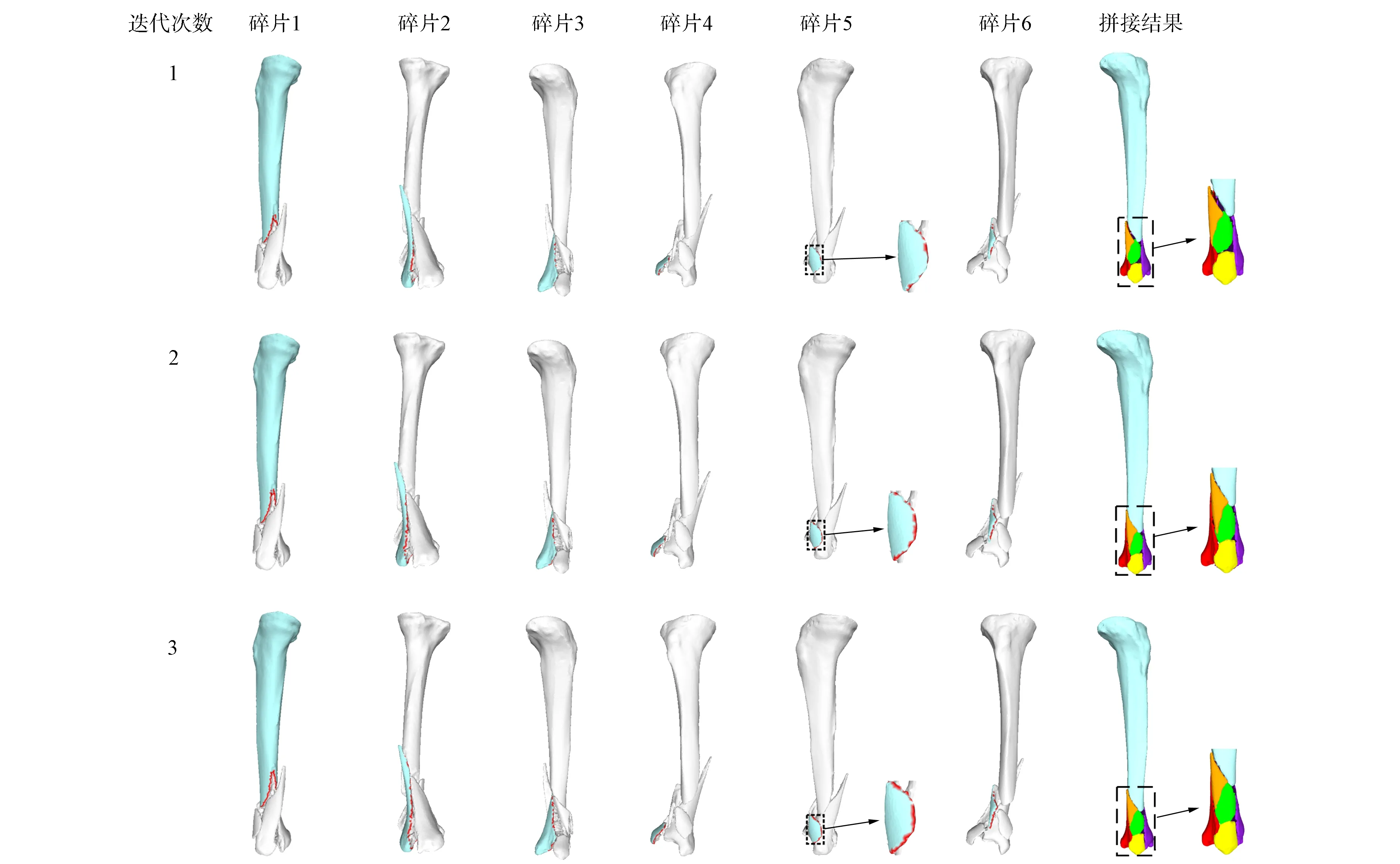
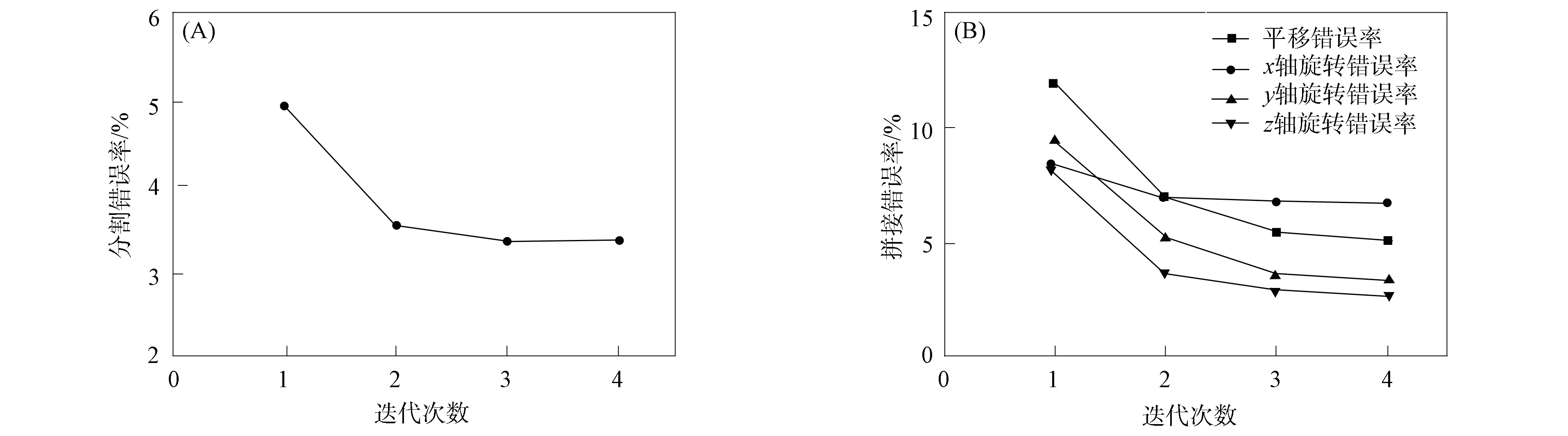
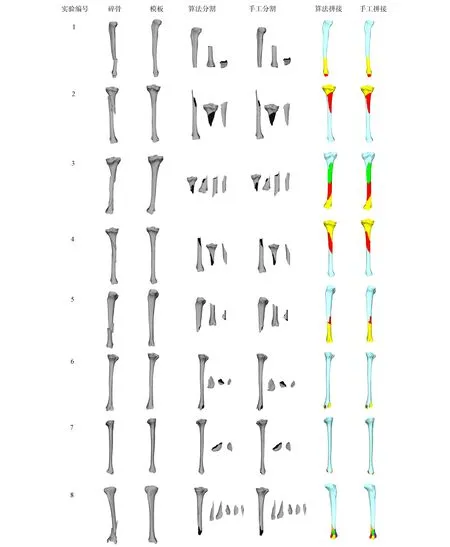
3) While (迭代次数k { 基于模板特征和碎骨特征将初步分割的碎骨配准到模板,然后用ICP算法修正匹配; break; k=k+1; }. 图3 碎骨外表面提取Fig.3 Extraction of external surface of broken bones 提取区分骨骼的外表面是一个二分类问题: 一类是碎骨外表面; 另一类是碎骨其他区域(包含骨骼内部组织和断裂区域). 本文选择PointNet++[5]分割神经网络,通过深度学习提取碎骨外表面. 训练数据为200个碎骨模型,人工标注每个顶点上这两类面的标签. 预测目标碎骨模型的外表面时,输出每个顶点属于内外表面的概率,网络预测正确率约为95%. 碎骨无断裂的平滑区域属于外表面概率较大,而靠近边界处的顶点以及碎骨内部属于外表面的概率较小. 碎骨外表面提取结果如图3所示,其中图3(B)为碎骨点云模型通过PointNet++神经网络预测后内外表面分割结果,黄色标记点为预测得到的碎骨外表面顶点,本文方法选用网络预测的中间结果,即内外表面概率作为方法的输入. 因此,为保证各碎骨的外表面不相邻,本文取外表面概率范围在[0.95,1]内的点,然后根据连通性,初步分割构成各碎骨的外表面,如图3(C)所示. 对碎骨内外表面概率进行预测的神经网络结构如图4所示,其中n=3. 网络结构主要包含3个阶段: 1) 多尺度分组抽象层,采用两种尺度进行分组,通过对点云模型下采样提取局部特征; 2) 特征传播层,对点云进行上采样,通过分层插值法传播特征; 3) 多层感知机,输出最终描述符. 分割神经网络的损失函数采用交叉熵函数,定义为 (1) 图4 PointNet++预测模型Fig.4 PointNet++ prediction model 模板匹配的目标是将每块碎骨匹配到对侧骨模板的对应区域. 本文先利用特征匹配初步配准碎骨和模板,然后用ICP算法进一步修正配准. 其中关键问题是计算碎骨特征. 骨骼特征分为对侧骨模板特征和初始碎骨特征. 本文采用深度神经网络PointNet++[5]回归预测. 碎骨配准到模板后,在每次迭代过程中都需计算碎骨特征,本文通过标签传递将对侧骨模板特征映射到碎骨. 为降低人工标注成本,本文利用一种基于可变形模板生成训练数据,该方法通过模板的参数化变形生成大量带特征的训练数据. 步骤如下: 先利用主成分分析法[34,36]构建参数化的健康骨骼形状统计模板; 然后取其平均模板(参数皆为0)做Laplace嵌入[37],即计算三维形状Laplace矩阵的特征值和特征向量,按特征值由小到大排序,取前30个特征值对应的特征向量,每个特征向量的维数等于模板骨骼的顶点数,从而生成每个顶点上的30维向量特征; 最后使模板参数变形的模型拓扑一致,将平均骨骼顶点上的向量特征映射到变形骨骼的对应顶点,形成训练数据. 利用完整骨骼进行训练,则该网络对于完整骨骼预测特征较好. 因此,为提高特征预测准确度,本文将所有碎骨外表面作为一个整体预测特征,而不用单个碎骨作为网络输入. 对外表面碎骨特征进行预测的神经网络结构如图4所示,其中n=30,其损失函数定义为 (2) 图5 碎骨模型上的曲率场和距离场Fig.5 Curvature field and distance field on broken bone model 区域增长停止条件同时满足碎片边界局部曲率条件及碎片边界与模板间的距离条件: (3) (4) 其中:p0为当前增长点,pi为p0测地距离为3 mm的邻域范围内第i个点,m为p0邻域范围内的点数;Cp0为p0的平均曲率,Cpi为pi的平均曲率;δc为曲率阈值,δc=0.008时实验结果最优;qNi为点pi在模板N上的欧氏距离最近点;δd为距离阈值,δd=0.01 mm时实验结果最优; 距离函数d定义为 (5) 本文实验数据为8例胫骨骨折双侧扫描临床病例,模板为碎骨对侧骨镜像后数据,均来自于南京医科大学附属常州第二人民医院. 其中4例为胫骨骨干骨折,4例为胫骨远端骨折,男女比例为5∶3. 三维碎骨与模板为CT影像双侧扫描数据,采用Mimics与3-Matic[38]软件进行三维重建与预处理,处理过程如下: 利用Mimics软件实现碎骨与对侧骨的三维重建; 利用3-Matic软件中网格优化对碎骨和对侧骨模型进行重网格,在不改变模型外形结构的情形下适当简化网格模型; 提取对侧骨的表面模型并进行镜像操作,得到碎骨模板数据. 本文实验中真实碎骨数据共208例,200例数据为PointNet++内外表面预测神经网络的训练数据,8例为实验测试数据,测试数据不包含于训练数据. 由于人体骨骼外表面形态相似,具有一定的统计特性,骨骼内部松质骨分布杂乱无章,因此200例训练数据能较好地区分碎骨内外表面. 6.2.1 实验过程 本文用一例复杂碎骨实例验证本文碎骨分割与拼接方法的有效性. 图6(A)为三维重建后的复杂碎骨,图6(B)为碎骨模板,模板是碎骨对侧骨镜像后的外表面模型. 本文方法碎骨分割与拼接过程如下: 1) 将碎骨点云模型输入到PointNet++分割神经网络中,预测得到碎骨点云模型内外表面顶点概率,提取外表面概率大于0.95的顶点,得到碎片互不相连的碎骨初步分割结果,如图6(C)所示; 2) 将碎骨初步分割点云模型转为网格模型,根据连通性将其自动分割为互不相连的碎骨碎片; 3) 将碎骨初步分割点云模型与模板点云模型输入到PointNet++回归预测网络中,预测得到碎骨初始特征与模板特征,分别如图6(D)和图6(E)所示; 4) 根据特征将碎骨初匹配到模板上,再根据ICP算法进一步修正匹配,如图6(F)所示; 5) 根据碎骨与模板间的距离差异与碎骨表面曲率信息进一步分割碎片边界; 6) 通过标签传递将模板特征传递到碎片上,更新碎片特征,根据特征再次进行匹配、分割,此过程迭代3次后收敛,碎片分割与匹配精度逐步提高. 标记每个碎片最终分割结果在模板上的对应点,当对下一个碎片进行分割时将不再匹配模板上已标记的区域. 对碎骨所有碎片依次执行上述步骤,图7为碎骨所有碎片3次迭代处理过程,碎片红色标记表示碎片分割边界,随着迭代次数的增加,碎片边界逐步优化,碎骨拼接结果接近健康骨骼状态. 图6 碎骨分割过程Fig.6 Segmentation process of broken bones 图7 碎骨3次迭代分割拼接过程Fig.7 Three iterations segmentation and splicing process of broken bones 本文方法分割与拼接迭代求精,随着迭代次数的增加,分割错误率与拼接错误率逐步下降. 图8(A)为该例碎骨随迭代次数增加分割错误率的变化情况,采用分类指标中错误率计算方法,定义为 error_rate=(FP+FN)/(P+N), (6) 其中FP表示算法分割错误三角面片数量,FN表示算法欠分割三角面片数量,P+N表示该模型三角面片总数量. 图8(B)为拼接错误率的变化情况,拼接错误率从平移相对误差以及x,y,z轴旋转相对误差评估,定义为 (7) 其中n表示碎骨包含的碎片个数,Δi表示第i个碎片的绝对误差,即手工测量值与算法测量值的绝对差值,Li表示手工测量值. 分割错误率与拼接错误率在3次迭代后收敛,为保证算法效率,本文方法迭代次数最终选择为3次. 图8 碎骨分割(A)与碎骨拼接(B)错误率随迭代次数的变化曲线Fig.8 Error rate curves of broken bone segmentation (A) and broken bone splicing (B) with number of iterations 6.2.2 实验结果 图9 碎骨分割与拼接结果Fig.9 Segmentation and splicing results of broken bones 本文对8例胫骨骨折临床病例进行分割与拼接实验,并将该方法分割、拼接结果与骨科医生使用的3-Matic软件手工分割、拼接结果进行对比,实验结果如图9所示. 图9记录了碎骨与模板数据:算法分割、拼接结果,手工分割、拼接结果. 由图9可见,本文方法能较好地实现碎骨分割与碎片拼接,接近手动分割与拼接结果. 下面对本文方法从两方面进行评估: 1) 本文算法的分割结果与手工分割结果进行对比; 2) 本文算法的拼接结果与手工拼接结果进行对比. 利用Dice系数[39]评估算法分割的精确度,实验结果列于表1. 表1列出了每个碎骨模型使用算法分割与手工分割两种方法最终得到的三角面片总数量,其中算法分割三角面片为算法最终分割结果,包含分割错误的三角面片. Dice系数是一种集合相似度度量函数,通常用于计算两个样本的相似度,范围为[0,1],Dice系数的值越接近1,说明相似度越高. 碎骨表面分割方法的Dice系数计算公式如下: (8) 其中|Fseg∩Fgt|表示与手工分割对比本文算法正确分割三角面片个数,|Fseg|表示算法分割三角面片个数,|Fgt|表示手工分割三角面片个数. 表1中Dice系数平均值为0.984 4. 由表1可见,本文方法分割结果与手动分割结果相比误差较小,在可接受范围内. 表1 碎骨分割结果 下面从平移误差、旋转误差两方面评估算法拼接的精确度,实验结果列于表2. 表2列出了8例碎骨所有碎片的平移误差与旋转误差,并计算了平移误差均值与旋转误差均值. 其中:平移误差采用均方根误差(RMSE)表示,定义为两种拼接碎片对应点间欧氏距离的均方根;旋转误差定义为算法拼接旋转角度与手工拼接旋转角度差值,用ICP算法计算手动拼接与算法拼接的刚体变换,先用矩阵R表示其旋转变换,再根据旋转矩阵R计算得到旋转误差α,β,θ(α,β,θ分别表示绕x,y,z轴旋转误差角度). 将本文方法拼接结果与手工拼接结果进行对比,8例碎骨所有碎片间平移误差均值为9.218 mm,旋转平均值为1.298°,其中x,y,z轴方向上的旋转误差均值分别为1.515°,1.139°,1.241°. 由表2可见,本文方法对大碎片的平移、旋转效果较好,碎片较小或碎片特征不明显时,平移、旋转误差较大,如实验1中碎片3,实验6中碎片3、4等. 通过与手工拼接结果比较,本文方法总体拼接误差较小,能满足临床医学碎骨拼接的要求. 表2 碎骨拼接结果 下面通过对单个骨折病例算法分割、拼接运行时间与手工分割、拼接时间进行对比评估算法的效率. 实验平台为VSCode Linux x64,搭建在Ubuntu18.04系统上,算法测试环境为NVIDIA Quadro RTX 6000 GPU,系统内存为16 GB. 实验结果列于表3. 由表3可见: 1) 本文方法对一个完整骨折病例的所有碎块进行分割与拼接修复时间为1~3 min,手工分割与拼接方法耗时为40~90 min,因此本文方法极大缩短了碎骨分割与拼接时间; 2) 碎骨分割、拼接耗时与碎骨碎裂个数相关,骨折碎片个数越多,算法运行时间越长. 本文方法对分割与拼接迭代进行,结果逐步求精,碎骨分割、拼接结果与手动分割、拼接结果相近,误差较小,耗时较短,在可接受范围内. 表3 碎骨分割拼接时间对比 为验证本文方法对不同网格密度的鲁棒性,从高、中、低三种网格密度进行验证,网格顶点数量分别约为20 000,10 000,5 000个. 本文从Dice系数、平移误差、旋转误差三方面评估不同网格密度下算法分割与拼接效果的鲁棒性,实验结果列于表4. 表4 网格密度实验结果 表4列出了8例骨折数据在高、中、低3种网格密度下算法分割与拼接的结果,与手动分割和拼接结果进行对比. 采用6.2.2中8例骨折数据进行格密度对比实验,利用在3种网格密度下Dice系数均值评估算法分割的鲁棒性,利用平移误差均值与旋转误差均值评估算法拼接的鲁棒性. 由表4可见,网格密度越高,Dice系数越高,平移误差与旋转误差越小. 图10为实验过程中一例碎骨在3种不同网格密度下算法的分割与拼接结果. 图10 不同网格密度分割与拼接结果Fig.10 Segmentation and splicing results of different grid densities 由图10可见,网格密度对实验结果有影响,模型精度越高,算法分割与拼接效果越好. 本文算法在高、中、低3种网格密度下分割、拼接结果与手动分割、拼接结果相近,误差较小,能满足术前规划实际要求. 将基于模板与数据驱动的拼接方法与ICP方法[35]以及文献[40]方法进行对比实验. 实验数据采用6.2.2中8例碎骨骨折数据,碎骨碎片采用手工分割方式提取. ICP方法实验是将碎骨碎片采用ICP算法与对侧骨模板直接匹配; 文献[40]方法实验是基于拼接思想,采用两两拼接方式,以两个碎片点云质心连线为扫描方向,采用距离滤波器提取两个碎片断裂边界接触区域,最终利用ICP算法匹配拼接. 下面从平移误差与旋转误差两方面评估3种拼接方法对碎骨骨折的复位效果,实验结果列于表5. 3种方法的平移误差与旋转误差均与手工拼接方法进行对比. 当碎骨碎片之间相对旋转角度较大或者碎片间距较大时,ICP方法与文献[40]方法都对初始位置较敏感,需进行手工粗匹配,图11为两例骨折数据在3种拼接方法下的实验结果. ICP方法与文献[40]方法对于多个碎片拼接的平移误差与旋转误差均较大,对小碎片位置匹配较差; 本文方法利用碎骨与模板间的特征密集对应关系进行粗匹配,再根据ICP算法进行精确匹配,碎片匹配精确度较高,拼接误差较小,可满足骨折术前规划的要求. 表5 不同拼接方法实验结果对比 图11 3种方法拼接结果对比Fig.11 Comparison of splicing results of 3 methods 综上所述,针对骨折发生随机、相互接触碎骨的边界分割困难、小碎骨丢失导致碎骨拼接较难的问题,本文提出了一种基于模板引导与数据驱动的三维碎骨修复方法. 该方法的核心思想是基于数据驱动初步提取碎骨表面,利用特征将碎骨与模板进行匹配,通过分割-拼接迭代求精,实现碎骨提取与碎骨拼接. 用8例胫骨骨折临床数据进行验证,所有实验结果均符合骨折修复术前规划实际要求,与手工分割与拼接结果相比,误差较小. 与目前已有方法相比,本文方法优点如下: 1) 实现了碎骨表面模型的提取,并完成了碎骨拼接修复; 2) 基于模板匹配更好地实现了碎骨边界分割,解决了因碎骨边界接触、边界特征不明显导致边界分割困难的问题; 3) 基于模板匹配实现碎骨修复可更好地解决因细小碎片丢失导致某些碎片边界吻合程度不高、碎片拼接困难的问题. 但本文方法还存在以下不足: 由于骨折发生随机,存在碎骨碎片较小,碎片特征不明显,导致小碎片特征匹配精度不高,匹配误差较大,所以小碎片的分割与拼接误差相对较大.
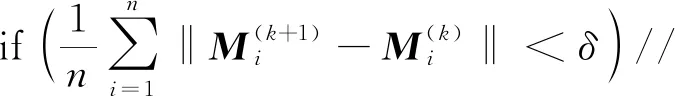
3 外表面提取与分割


4 模板匹配
4.1 基于形状统计模板的训练数据生成
4.2 基于上下文形状的碎骨特征预测

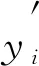
5 计算碎片边界



6 实 验
6.1 骨骼数据
6.2 实验过程及结果
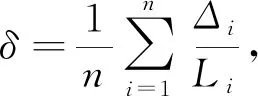




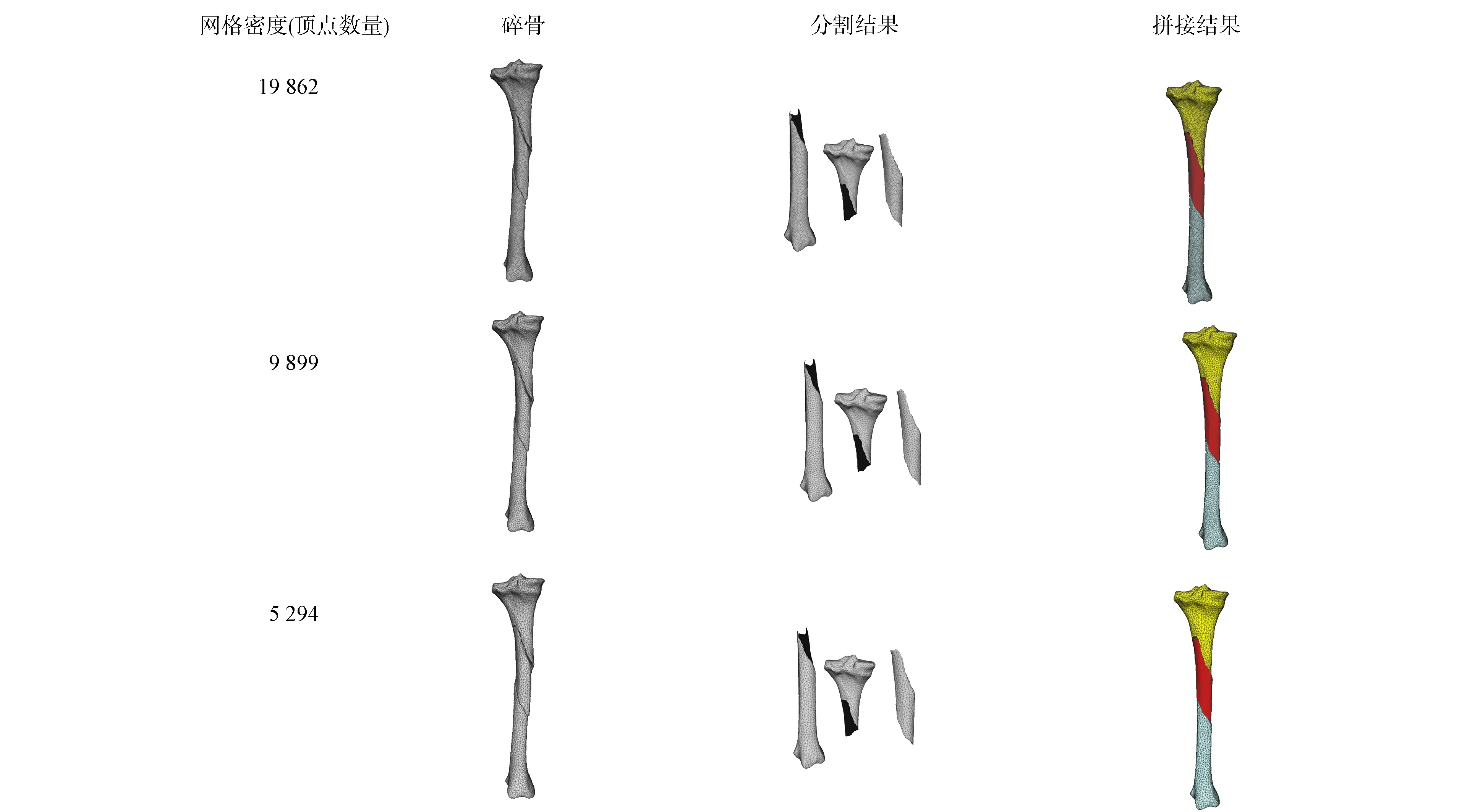
6.3 网格密度对比实验

6.4 碎骨拼接对比实验


