基于黏着理论的牵引器驱动轮力学分析及优化*

肖晓华 代继樑 王昆鹏 赵建国

(1. 西南石油大学机电工程学院 2. 西南石油大学油气藏地质开发工程国家重点实验室 3.中国人民解放军第五七一九工厂)

0 引 言

目前，水平井已经大规模应用于各类油气藏，水平井的数量和水平延伸长度都在不断增加，使连续管的延伸和测井工具的输送面临很大挑战[1-4]。采用井下牵引器牵引连续管和输送测井工具具有成本低及耗时少等优点。常见牵引器有轮式和伸缩式两种，其中轮式牵引器具有体积小、井径适应性强及可用范围广等特点。轮式牵引器的牵引力由驱动轮与套管的接触摩擦力决定，因此对驱动轮与套管的接触进行研究和优化对提升牵引器牵引能力具有重要意义。

综上所述，环孢素对降植烷致SLE模型小鼠有一定的肾组织保护作用，对其肾损伤有一定改善作用，其机制可能与抑制TWEAK-p38MAPK信号通路有关。

影响驱动轮与套管接触产生摩擦力的因素很多，传统的计算采用经验摩擦因数与正压力来处理牵引力[5-8]。为了增大接触摩擦力，轮式牵引器的驱动轮多为齿形轮，驱动牵引力达到3 000 N以上，齿尖与壁面的接触面积很小。这种情况下，通常在转动过程中齿尖对套管会产生微小嵌入，进而使管壁接触区域产生塑性变形，并随着转动可能产生微小沟痕。这种接触状态显然与传统滑动摩擦状态不同，通常试验所得的摩擦因数不适用于此类摩擦力的计算。

对于牵引器驱动轮与套管的相互作用，常旭等[9]采用滑移线理论，确定了正压力与塑性区面积和压痕形状的关系，但未给出摩擦因数与摩擦力的计算方法；刘清友等[10-11]考虑犁沟效应，建立了驱动轮和套管的力学模型，提出了压痕区面积的计算方法，但都未对驱动轮摩擦力进行深入分析，后者计算摩擦因数采用的尖锐齿形及棱柱齿形模型也不符合实际情况。因此，提出一种更为合理的齿形，完善轮齿与套管壁面接触摩擦模型，明确实际状态下摩擦因数的取值方法和影响摩擦因数的主控因素十分必要。

根据摩擦学理论[12-13]，仅考虑犁沟效应计算驱动轮和套管的摩擦力不完善。犁沟效应是指硬金属的粗糙峰嵌入软金属后，在滑动过程中推挤软金属，使之塑性流动并犁出一条沟槽的过程。而硬表面的粗糙峰在法向载荷的作用下嵌入软表面，在齿峰嵌入和滑动时，除犁沟力之外，材料的剪应力也不应忽视。因为二者的接触面积由两部分组成：一是发生黏着效应的面积，滑动时发生剪切；另一部分是犁沟效应的作用面积，滑动时硬峰推挤软材料。此种状态的接触面积远小于表面面积，接触部位多处于塑性状态，适用于黏着理论。

本文结合牵引器的应用需求，提出了耐用性更好的驱动轮六面体梯形齿结构，引入黏着理论，同时考虑黏着效应和犁沟效应，建立驱动轮与套管之间的力学模型，推导相应效应下的摩擦因数计算公式，明确了影响摩擦因数的主控因素；采用数值模拟的方法对驱动轮齿参数进行优化，得到了对套管损伤较轻情况下驱动轮齿的结构参数，以及此条件下驱动轮与套管之间的摩擦因数。所得结论可为轮式牵引器牵引力的提高和驱动轮的设计提供理论基础和设计参考。

1 驱动轮力学分析

通过上文分析，驱动轮和套管在同时考虑黏着效应和犁沟效应时，摩擦力应是犁沟效应和黏着效应的总和[14]。

1.1 犁沟效应下的摩擦因数

通常情况下，为了提高驱动轮的耐磨性，驱动轮材料远比套管材料硬，即驱动轮材料屈服强度远大于套管材料，在载荷和正压力作用下，驱动轮会压入套管产生犁沟效应。

三抓绩效考评运行创新，构建长效保障机制。积极推进农开项目绩效管理，开展项目验收考评工作，构建考评、绩效相结合的长效保障机制，对考评差、工程质保期内工程质量反馈差的建设单位纳入黑名单，限制其准入，确保工程项目保质保量地实现预期目标。

本文设计的驱动轮齿形为六面体梯形齿，如图1所示。该种齿形相比于尖角齿有更好的耐用性和更强的抗剪切能力，对套管的损伤较轻。

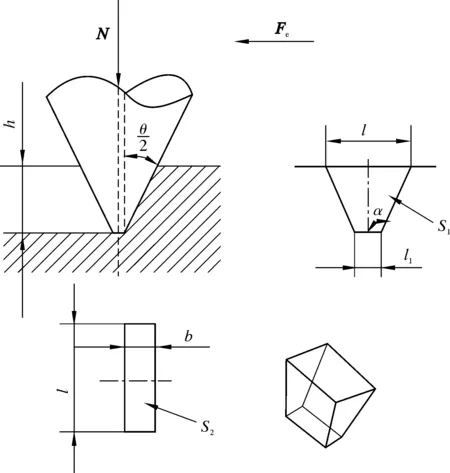
图1 驱动轮齿形结构力学模型Fig.1 Mechanical model of driving wheel tooth profile structure

其接触面的水平投影为梯形，假设梯形的上底长为l，嵌入深度为h，驱动轮齿倾角为α，驱动轮的齿顶角为θ，犁沟效应下的摩擦力为Fe，则其下底长l1为：

l1=l-2htan(α-90°)

(1)

水平投影面积为：

(2)

将式(6)带入式(13)可得：

S2=lb

(3)

(4)

在套管为各向同性材料条件下，正压力为：

N=S2τb

(5)

式中：τb为嵌入的剪切力，Pa，它只与滑动的速度和润滑的状态有关，数值上约等于套管金属材料的屈服极限。

将许用剪切应力[τ]取为屈服强度的[20]，计算得齿顶角的取值范围：56.6°≤θ≤123.4°，该范围是驱动轮与套管保持自锁且强度足够条件下的最佳取值范围。

Fe=S1σs

(6)

式中：Fe为犁沟效应摩擦力,N；σs为套管材料的屈服极限,Pa。

因此，犁沟效应下的摩擦因数为：

(7)

联立式(1)～式(7)可得摩擦因数：

但他一上车后立即“原形毕露”，向助手发泄怒火：“那是场灾难。根本不该让我和那个女人见面。谁出的主意？”布朗形容道：“(她)什么都问。她就是那种偏执的女人。”

(8)

由式(8)可知，在犁沟效应下，驱动轮与套管之间的摩擦因数与驱动轮齿顶角θ、齿倾角α、下底长l1和嵌入深度h有关。

1.2 黏着效应下的摩擦因数

黏着效应是由于分子的活动性和分子力的作用使固体黏附在一起，进而产生了滑动阻力。黏着效应可以根据Israelachvili提出的“鹅卵石”模型进行分析[15]。图2为黏着效应摩擦的“鹅卵石”模型图。

式中：Fτ为驱动轮齿的剪切力。

图2 黏着效应摩擦的“鹅卵石”模型Fig.2 “Cobblestone” model of adhesion effect friction

黏着效应产生的阻力为[16]：

(9)

式中：Fn为黏着效应摩擦力，N；Do为相邻原子质心之间距离，m；m为原子质量，kg；a0为晶格常数，m；v为相对滑动速度，m/s；ε为温度扩散系数，m2/s；E为套管材料弹性模量，GPa；G为套管材料剪切模量，GPa；γ为表面能密度，J/m2；Δd为原子从波谷运动到波峰所经历的切向距离，m；ΔD为原子从波谷运动到波峰所经历的法向距离，m。

由式(5)和式(9)可得黏着效应下驱动轮与套管的摩擦因数：

(10)

1.3 驱动轮与管壁总摩擦因数

轮式牵引器的驱动轮材料选用40CrMoTi，屈服强度835 MPa，抗拉强度1 080 MPa，泊松比0.3；套管钢级选用油田常用钢级J55，屈服强度379 MPa，抗拉强度517 MPa。

其他参数取值为[17]：Do=2.48×10-10m，m=1×10-29kg，a0=2.86×10-10m，v=0.16 m/s，ε=1.59×10-5m2/s，E=125 GPa，G=46.4 GPa，γ=2.417 J/m2，Δd=1.43×10-10m，ΔD=7.254×10-9m。

联合式(8)和式(10)，可得考虑犁沟效应和黏着效应的总摩擦因数：

(11)

由式(11)可知，驱动轮与套管之间的总摩擦因数与驱动轮齿顶角θ、齿倾角α、下底长l1和嵌入深度h有关。

2 驱动轮轮齿最优参数仿真设计

在正压力与驱动轮和套管材料一定的情况下，驱动轮的齿形结构是影响其与井壁接触效果的关键因素。笔者利用ABAQUS有限元软件对驱动轮的轮齿参数进行优化，分析不同参数下轮齿嵌入套管内壁的应力及塑性应变的变化，确定最佳的轮齿设计值。

2.1 齿顶角范围确定

在考虑齿顶角时，为防止出现干涉，通常假设驱动轮相邻两齿不同时接触套管，则齿顶的受力分析如图3所示。图3中F1为电机力矩等效于O点的驱动力；F2为轮式牵引器单个驱动轮所受牵引力；在Ⅰ区内，驱动轮齿沿套管壁接触点继续压入管内；在Ⅱ区内，驱动轮齿与套管壁形成自锁；在Ⅲ区内，驱动轮齿与套管壁面打滑。

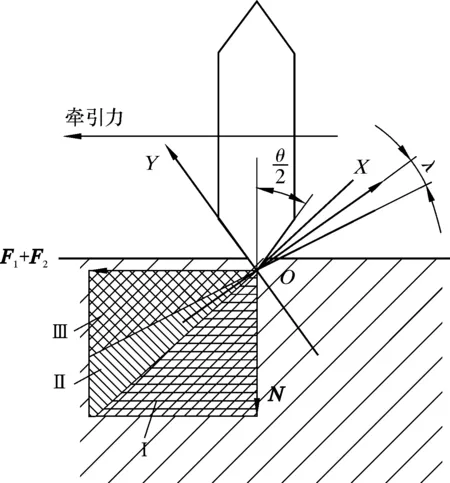
图3 驱动轮齿顶受力分析图Fig.3 Analysis of the force on the tooth top of the driving wheel

为了确保驱动轮有效牵引，驱动力、牵引力和正压力的合力应落在Ⅱ区内。通过力学分析可得牵引力和正压力与齿顶角的关系：

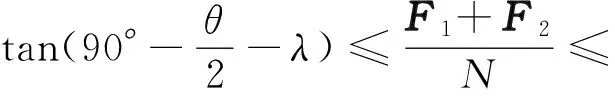
(12)

式中：λ为摩擦角，在驱动轮轮齿与套管之间无润滑状态下静摩擦因数μ1=0.3[18]，于是λ=tan-1μ1=16.7°。

由式(12)可知，在驱动力和牵引力一定时，齿顶角与正压力呈正相关，但是齿顶角过小时，会减小轮齿的屈服强度[19]。因此，需要得到保证轮齿强度下的齿顶角的取值范围。齿顶所受剪切力τ应小于许用剪切强度。由剪切力定义及式(5)～式(6)可得：

(13)

1 6个月以下的宝宝体温超过38oC，6个月以上的宝宝体温超过39oC，需要就医，不超过可以物理降温。

接触面的投影面积为：

(14)

将上式带入式(12)可得：

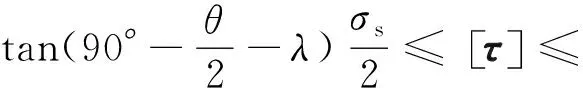
(15)

犁沟效应所需摩擦力为：

2.2 轮齿仿真模型建立

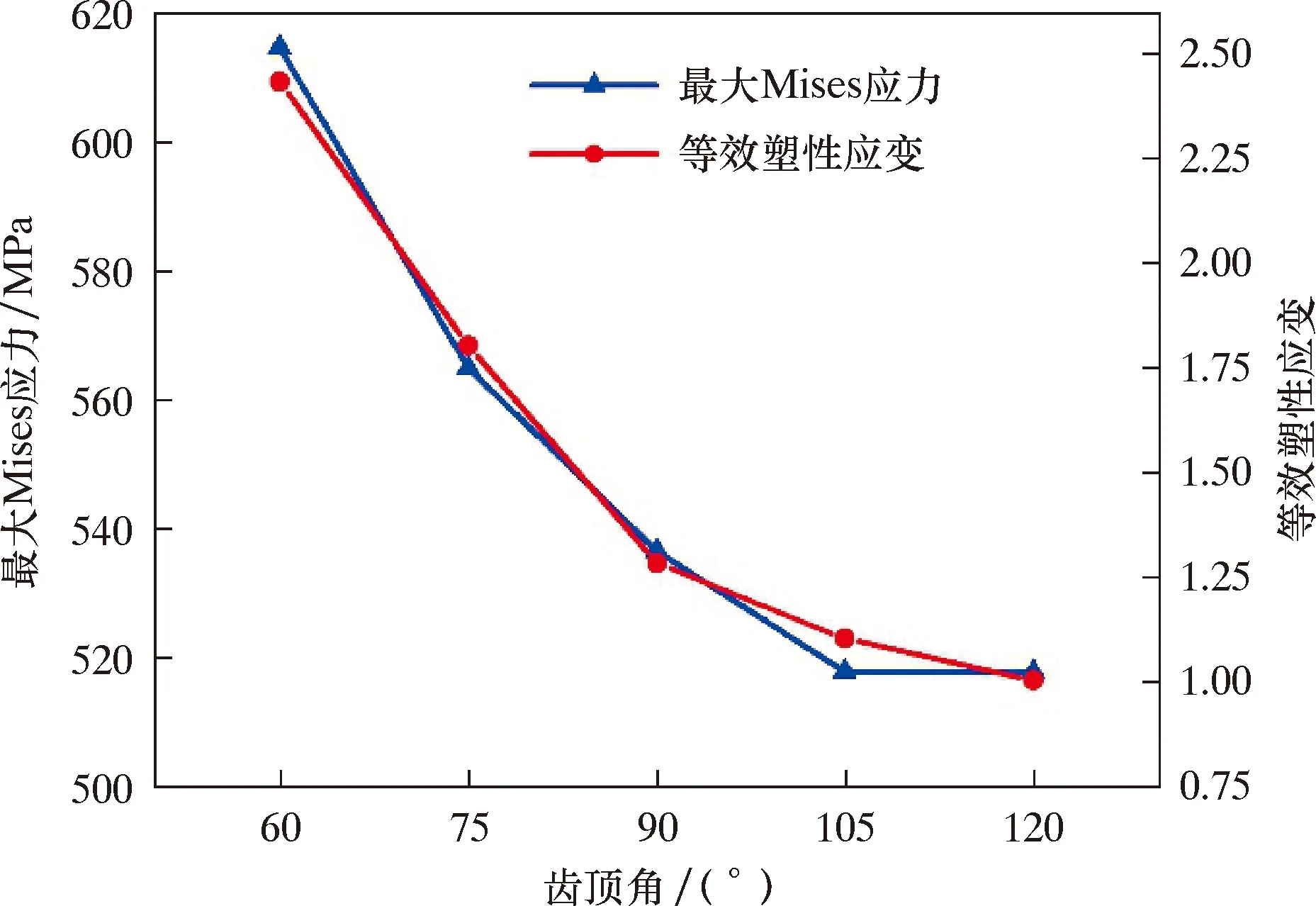
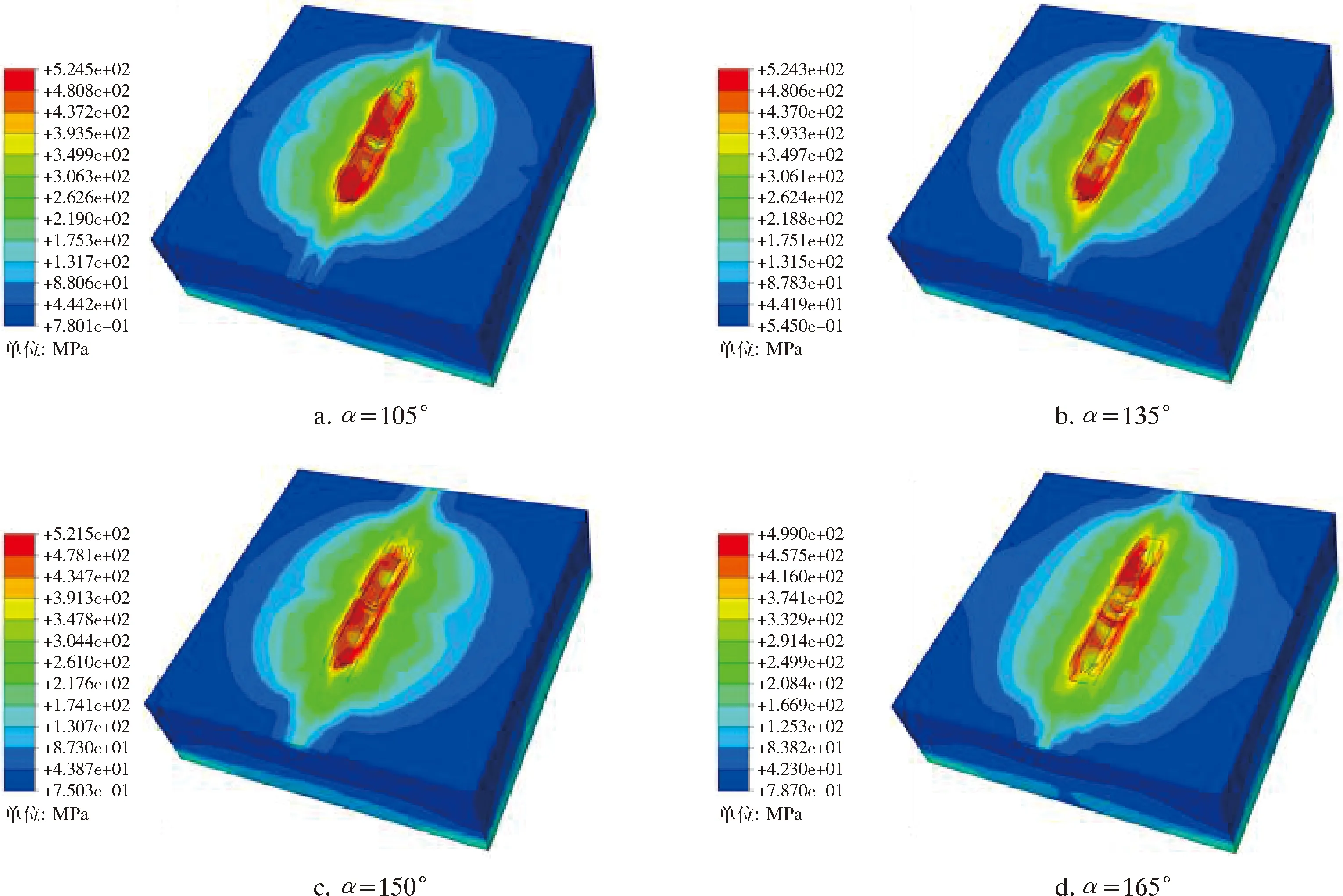
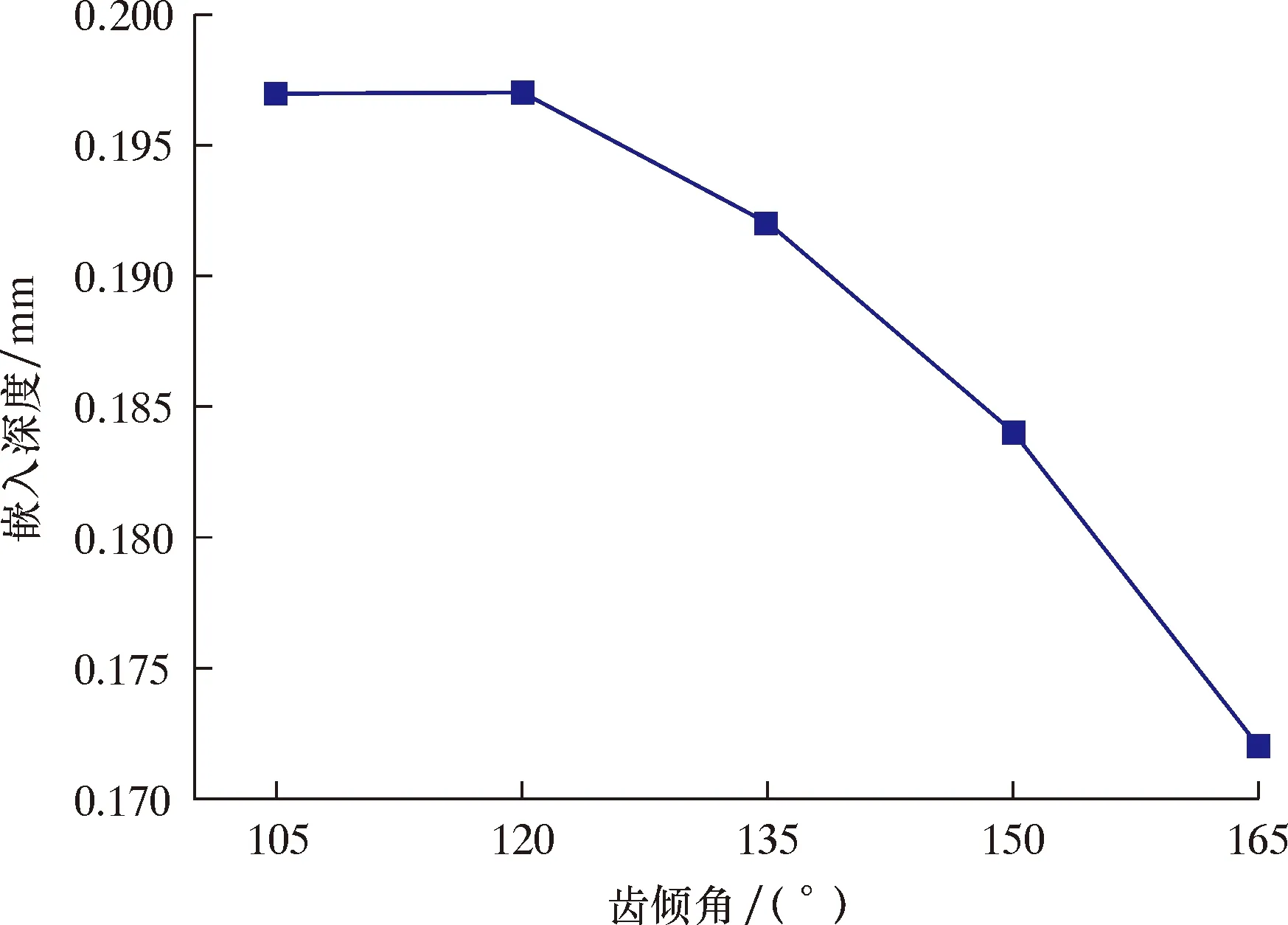
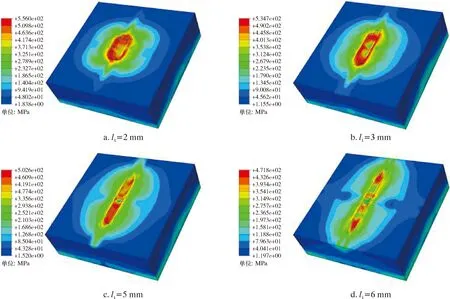
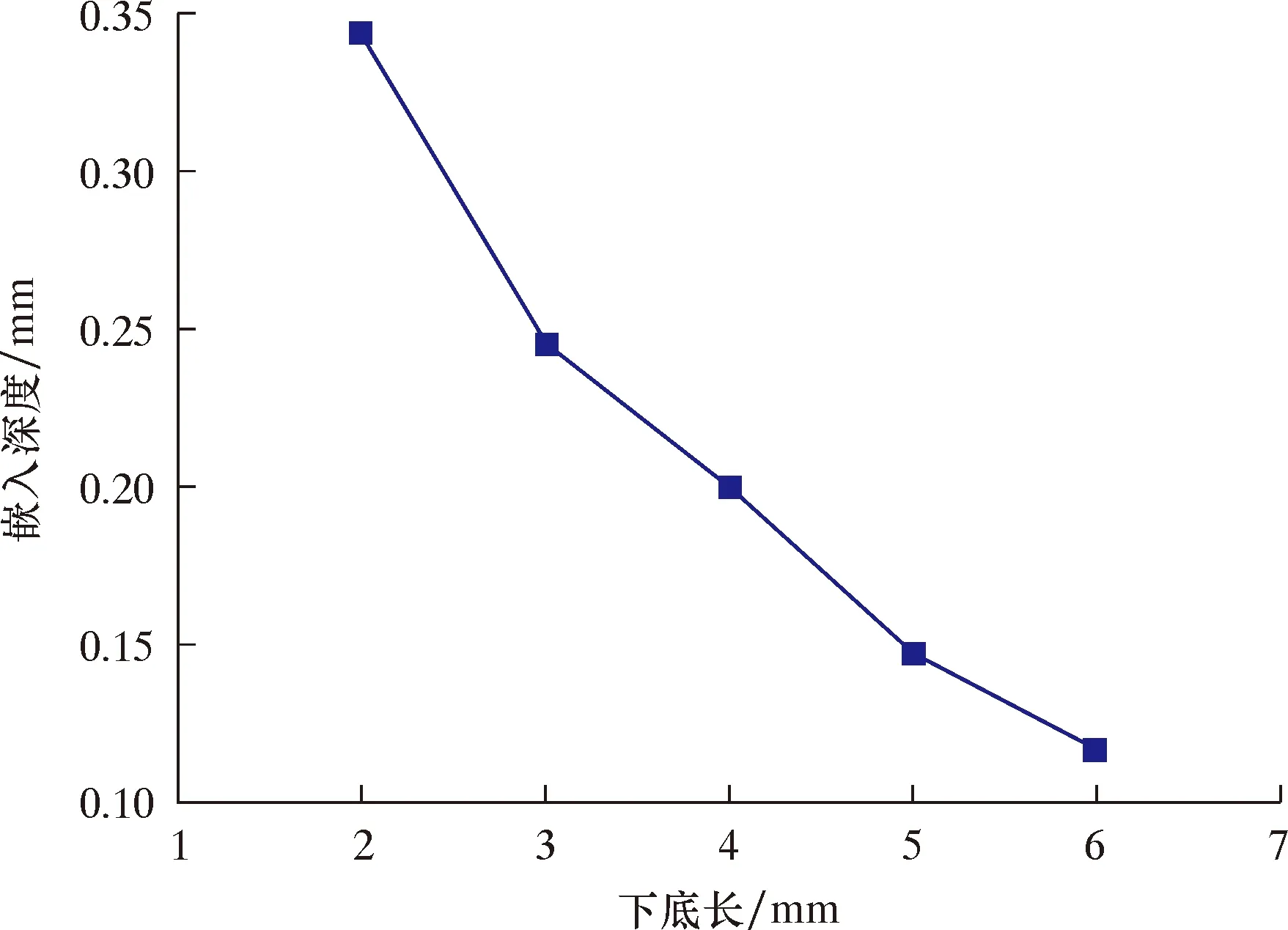
设定驱动轮在套管壁上运动时，一个时间段内只有一个轮齿与管壁接触，选取单齿为研究对象。通过前文分析，齿顶角θ的取值范围为56.6°≤θ≤123.4°，齿倾角α的取值范围为90°<α<180°，下底长l1的取值范围为0 mm

关于马克思恩格斯的生态观，曾繁仁并没有选择全盘接收，而是指出了他们的理论存在无法避免的历史局限性。地球上的石油和树木，在马克思眼里只有当它们为人们所用时才具有使用价值，其实不然，它们除了自身的价值还拥有其承载限度。可见，他们对生态、自然的认识不够全面和深入。

表1 驱动轮轮齿参数取值Table 1 Values of driving wheel tooth parameters

简化后的单齿套管模型如图4所示。

图4 简化后单齿套管模型Fig.4 Simplified single tooth casing model

模型设置分析步为：约束套管全部自由度，约束驱动轮齿除了Z轴方向的全部自由度，对驱动轮齿施加正压力2 000 N，驱动轮向下与套管接触，完全接触之后观察套管的变化情况。

2.3 轮齿参数优化

2.3.1 齿顶角

在轮齿倾角120°、下底长4 mm的条件下，齿顶角取值见表1。不同齿顶角时套管内壁接触应力云图如图5所示。

2016年南海东部石油钻井平台海事业务，由广东海事局授权惠州海事局进行监管，随着南海东部油气开发规模不断加大，惠州附近海域油气平台及其辅助船舶生产作业活动日趋频繁，通航流量和口岸业务增长迅猛，对海事部门依法履行监管和服务职责提出了新的要求。

(1)随驱动轮下底长的增大，嵌入深度减小，且减小趋势逐渐放缓；套管的等效塑性应变逐渐减小，同样趋势逐渐放缓；套管的最大Mises应力逐渐减小。

图5 不同齿顶角时管壁应力云图Fig.5 Stress distribution on casing wall with different tooth crest angles

图6 不同齿顶角时嵌入深度曲线Fig.6 Embedding depth curve at different tooth crest angles

图7 不同齿顶角时套管的最大Mises应力和等效塑性应变曲线Fig.7 Stress and plastic strain curves of casing with different tooth crest angles

由图5～图7可知：

(1)随着齿顶角的逐渐增大，驱动轮的嵌入深度、等效塑性应变和套管的最大Mises应力逐渐减小，最大应力为614.5 MPa，最小应力为517.5 MPa；驱动轮的嵌入深度呈线性变化，套管的最大Mises应力和等效塑性应变变化趋势逐渐变缓。

(2)驱动轮齿顶角在60°～120°区间时，套管的最大Mises应力都已经超过了其材料的屈服极限(379 MPa)，说明套管壁面接触部位为塑性变形，驱动轮齿已经嵌入套管内，产生了犁沟效应。

由图11～图13可知：

(3)在驱动轮齿顶角为60°时，嵌入深度和最大Mises应力最大，分别为0.307 mm和614.5 MPa，同时等效塑性应变最大，远远超过了套管的屈服极限，对套管损伤最大；当驱动轮齿顶角为120°时，套管的最大Mises应力为517.6 MPa，等效塑性应变为1，与相邻的齿顶角105°时相差不大，但嵌入深度比105°时要小不少，嵌入深度过小容易打滑和造成牵引力不足；当驱动轮齿顶角为105°时，套管的最大Mises应力和等效塑性应变变化放缓，变化值很小，对套管的损伤也很小，而嵌入深度达到了0.2 mm，远大于齿顶角120°时的嵌入深度，齿顶角105°为驱动轮齿顶角变化的拐点，故选择105°为齿顶角的优选值。

2.3.2 齿倾角

已知齿顶角优选为105°，固定下底长为4 mm，则在该条件下不同齿倾角时套管内壁的应力云图如图8所示。

图8 不同齿倾角时管壁应力云图Fig.8 The stress distribution of the casing with different tooth inclination angles

在齿顶角为105°、下底长为4 mm条件下，不同齿倾角时嵌入深度曲线、套管的应力曲线和塑性应变曲线分别如图9和图10所示。

图9 不同齿倾角时嵌入深度曲线Fig.9 Embedding depth curve at different tooth inclination angles

由图8～图10可知：

(1)随齿倾角的逐渐增大，套管的最大Mises应力先变小，后增大，再减小；驱动轮的嵌入深度和套管的等效塑性应变逐渐减小。最大Mises应力在105°～135°时产生先变小后变大的趋势，可能是因为驱动轮对套管的作用从剪切变为挤压而造成。

(2)当驱动轮齿倾角为105°时，驱动轮的嵌入深度最深，同时套管的最大Mises应力最大，为524.5 MPa，等效塑性应变达到1.2，套管变形最大，对套管损伤最大；当驱动轮齿倾角为165°时，套管最大Mises应力和等效塑性应变均为最小，同时嵌入深度最小；当驱动轮齿倾角为120°时，套管的最大Mises应力为517.6 MPa，相对于其他齿倾角对应应力值较小，等效塑性应变呈现稳定减小，嵌入深度达到0.197 mm，因此齿倾角的优选值为120°。

图10 不同齿倾角时套管应力和塑性应变曲线Fig.10 Casing stress and plastic strain curves at different tooth inclination angles

2.3.3 下底长

蛋白定量采用Bradford法，波长595 nm测定蛋白浓度，用标准牛血清白蛋白绘制标准曲线，对制备样品蛋白溶液定量。

众多的家政企业在各个角度做了众多的尝试，推动了家政服务业整体供给在规模和结构化发展方面有了较大的提升，但优质的家政服务人员供给并未达到想象中的高比例，还需从培训端进一步的聚焦和发力，才能推动整个家政服务行业的高质量发展。

已知优选的齿顶角为105°，齿倾角为120°，在该条件下不同下底长时套管内壁的应力云图如图11所示。

图11 不同下底长时管壁应力云图Fig.11 The casing wall stress distribution with different bottom lengths

在齿顶角为105°、齿倾角为120°情况下，不同下底长时驱动轮嵌入套管的深度曲线、套管的应力曲线和塑性应变曲线分别如图12和图13所示。

图12 不同下底长时嵌入深度曲线Fig.12 Embedding depth curve with different bottom lengths

图13 不同下底长时套管的应力变化曲线和塑性变形曲线Fig.13 Stress and plastic deformation curve of casing with different bottom lengths

某些医院对于绩效管理缺乏深入认知，相关工作人员对绩效管理认识上还比较肤浅，没有深刻认识到绩效管理对于医院发展的重要作用，与此同时，缺乏对绩效管理进行合理、良好定位，这样就导致医院后期工作难以得到顺利有效开展。绩效管理质量偏低，医院收益相对而言较低。

齿倾角120°、下底长4 mm条件下，不同齿顶角时嵌入深度、套管的应力曲线和塑性应变曲线分别如图6和图7所示。

(2)当驱动轮下底长为2 mm时，驱动轮嵌入深度最大，其值为0.344 mm，套管的最大Mises应力为556.0 MPa，等效塑性应变最大，对套管损伤最大；当驱动轮下底长为6 mm时，套管的最大Mises应力为471.8 MPa，对套管损伤较小，等效塑性应变较小，但驱动轮嵌入深度为0.117 mm，嵌入深度较小，会引起驱动轮齿滑出套管内壁，造成打滑现象；当驱动轮下底长为4 mm时，等效塑性应变处于缓慢下降阶段，套管的最大Mises应力减小趋势开始放缓，为套管最大Mises应力的拐点，此时嵌入深度达到了0.200 mm，因此优选出下底长为4 mm。

综上所述，选用齿顶角θ=105°、齿倾角α=120°、下底长l1=4 mm为最佳的驱动轮轮齿参数，此时轮齿对套管壁产生的损伤最轻，但能产生较大的摩擦力。

3 总摩擦因数优化

考虑黏着效应下驱动轮与套管之间的总摩擦因数计算式如式(11)所示。

将驱动轮齿顶角θ、齿倾角α、下底长l1和嵌入深度h的优化值带入式(8)，得到驱动轮与套管在犁沟效应下的摩擦因数μ1=0.746。

针对上述问题，人大工作者须认识到自身存在的不足，要加强对监督议题相关内容的学习，了解掌握党和国家的相关政策、具体的法律规定、外地的经验做法以及本地实际情况等，力求比被监督者站得更高、看得更远；要沉下心去，深入基层，通过面对面与群众交流、实地察看、问卷调查等多种手段，掌握群众真实意愿，全面了解工作开展情况，对工作取得的成绩、存在的问题做到心中有数，力求所提建议切实可行。

将相关参数带入式(10)可得黏着效应的摩擦因数μ2≈0.300。

将μ1、μ2带入式(11)可得总的优化摩擦因数μ=1.046。

4 结 论

(1)提出了一种新的基于黏着理论的驱动轮力学分析方法，得到驱动轮与套管之间的摩擦因数应为黏着效应摩擦因数和犁沟效应摩擦因数之和。

现阶段，燃气企业已经把现代化管理系统应用其中，以此实现对企业财务情况的审核和监管，但是从实际角度来说，企业即便把信息化管理方式引进其中，但是受到原始管理理念的影响，应用的财务管理模式过于传统性，没有将信息化管理系统自身作用充分发挥，导致信息化资源的大量浪费。并且，企业在引进信息化系统之后，没有根据系统要求来进行对应设施的研发和应用，授权管理不规范，使得不能借助信息化手段加以科学把控。

术后若发生低血压,应尽快实施扩容治疗。若血压无法很快恢复正常,应该静脉滴注去甲肾上腺素,直到恢复正常血压。

(2)提出了符合实际的驱动轮六面体梯形齿，并进行了力学分析，得到了驱动轮与套管之间摩擦因数的取值方法和影响摩擦因数的主控因素。

第二层强风化混合花岗岩厚度3～5m，RQD<25，天然重度平均值20.4kN/m3。Ra平均值4.0MPa，标准值3.8MPa。C=20kPa，Φ=35°，fak=400kPa。

(3)利用数值仿真分析软件建立了驱动轮与套管之间的相互作用模型，得到了在套管损伤较轻的情况下，驱动轮齿的最优参数，即齿顶角θ=105°、齿倾角α=120°、下底长l1=4 mm。通过摩擦因数的取值方法和驱动轮齿的最优参数，则基于黏着理论的驱动轮与套管之间的摩擦因数为1.046。