基于三阶谐振网络的恒定输出型ECPT系统

刁勤晴，谢诗云

（1.重庆理工大学 两江人工智能学院，重庆 401135；2.重庆理工大学 电气与电子工程学院，重庆 400054）

电场耦合电能传输技术（electric-field coupled power transfer，ECPT）是一种以金属导体作为电场耦合机构，高频电场作为能量介质的无线传能方式［1-3］。耦合机构的外形具有成本低、简易轻薄、可塑性强的特点；机构中的耦合电场主要集中在发射与接收电极之间，因而具有对周围的金属导体不会产生涡流损耗，且对周围环境产生的电磁干扰较低的特点［2］。上述特点使得ECPT系统与感应式无线电能传输系统（inductive power transfer，IPT）能够实现优势互补。目前，围绕ECPT系统在电动汽车、便携式电子产品、照明LED、工业机器人、航行器等领域的应用，国内外的专家学者已展开了大量理论研究，并在系统的逆变器效率提升、谐振网络传输特性、耦合机构电场分布、输出电压/电流控制等方面取得了诸多成果［4-6］。

在实际应用中，大多数用电设备要求其输入电源具有恒压特性；部分设备则需要具有恒流输出特性的电源，如照明LED；还有一些设备在不同的运行阶段需要电源能够在恒流源和恒压源之间进行转换，如锂电池的充电［4］。针对用电设备对电源输入特性的需求，现有文献在ECPT系统的实现方式依据调节对象可以分为4种：①调节发射端或接收端中的功率变换电路。如苏玉刚等［7］基于NSGA-Ⅱ智能算法和LQG控制算法来调节逆变器的移相角实现系统的恒定电压输出；②控制耦合机构的极板数量及位置。如Chao L等［8］通过调节阵列式耦合机构的发射极板的数量以及等效补偿电感来实现恒定电压输出；③利用谐振网络的特性。如Xia C等［4］利用T型CLC（电容-电感-电容）谐振网络的传输特性设计了一种恒流输出ECPT系统；④混合方式。如Abramov E等［9］构建了一种双闭环恒功率输出ECPT系统，通过同时调节发射端逆变器的工作频率以及谐振网络的等效电感来维持输出功率处于设定值。

以上4种方式均能实现ECPT系统的恒定输出，其中，利用谐振网络传输特性的方式无需额外设置检测与通信电路，且系统谐振网络输入阻抗特性始终处于零相角状态，因而系统的电路复杂度及整体成本相对较低同时具有较高的传输效率。鉴于此方式的特点，相关文献提出了多种具有恒定输出特性的谐振网络。在感应式WPT（wireless power transfer）系统方面，现有文献分析了二阶Γ型、三阶T型和四阶F型拓扑形式的传输特性，分别给出了具有恒压或恒流输出特性的LC/S、T-LCL、F-LCCL等电路形式［10-12］。然而，由于耦合机构特性的区别，感应式WPT系统的谐振电路形式并不能直接应用于ECPT系统。因为感应式WPT系统的耦合机构本质上是一个松耦合变压器，所以谐振电路除了具有输出恒定特性，同时还要补偿发射和接收线圈的漏感；而ECPT系统的耦合机构则可等效为一个带有内阻的电容器，机构的等效容抗可通过与之串联的电感进行补偿［8］。

考虑到耦合机构性质的区别，苏玉刚等［13］围绕ECPT系统的特点并借鉴感应式WPT系统的分析方法，分析了T-LCL和Π-CLC谐振网络的输入与输出增益函数，分别给出2种网络在恒流和恒压输出条件下的参数约束关系，并基于2种网络设计了一种恒压型ECPT系统；谢诗云等［14］分析了F-LCLC网络在恒压输出条件下的电路参数，建立了一种双侧F型恒压输出系统；苏玉刚等［15］利用Π-CLC谐振网络的恒压传输特性，给出了耦合机构的调谐方法并设计了一种Π-S复合网络的恒压型ECPT系统。通过对ECPT相关文献的分析，发现具有恒定输出特性的谐振拓扑形式较多，且研究的内容主要集中于特定拓扑形式中恒定输出条件下的谐振元件参数约束关系。然而，对这些基于特定拓扑形式的参数约束关系之间的内在联系以及谐振网络输出恒定的一般性条件尚未进行研究。另外，现有的具有恒定输出特性的谐振电路形式较多，因而如何面向不同应用场合选择相适应的拓扑形式并设计其参数成为关键的问题，相关的选择依据及设计方法并未见文献进行研究。

针对上述问题，本文建立了在恒压源和恒流源激励下二端口网络输出恒定的一般性参数约束条件，基于此条件分析了三阶谐振拓扑的输出特性，并给出了具有输出恒定时元件之间的参数关系，进而给出了不同拓扑下具有恒定输出特性的谐振电路形式及其输入输出增益函数。据此推导了该电路形式的全谐波畸变率（total harmonics distortion，THD）及输入阻抗一般性表达式，对比分析了不同谐振电路的谐波抑制性能和参数敏感性，从而给出了面向不同应用场合谐振电路的选择依据及其参数设计流程。最后，搭建了基于三阶T-Π网络的恒压型ECPT样机系统，从而验证了所分析的谐振网络的传输特性准确性及其参数设计方法的有效性。

1 基于三阶谐振网络的恒压/恒流型ECPT系统结构

基于三阶谐振网络的恒定输出型ECPT系统的典型结构如图1所示。发射单元由输入直流源、高频逆变器、三阶谐振网络组成；耦合单元包括补偿电感和耦合机构；接收单元则由谐振网络、整流和滤波电路、负载等效电阻构成。其中，输入电源一般采用直流电压源，电流源则常用于发射端谐振网络呈高频低阻抗特性的场合［16］；滤波电路通常采用单个电容，当需要更小的输出纹波时则使用由电感和电容组成的滤波电路。

图1 基于三阶谐振网络的恒压/恒流型ECPT系统结构电路图

系统的工作原理为：输入电源经过逆变器产生高频交流电，再由发射端谐振网络抬升至耦合机构所需的高激励电压，耦合机构中交变电场在接收极板产生电势差，再通过接收端谐振网络后整流滤波供给负载。其中，耦合机构可等效为2个电容器CS1和CS2，并通过串联电感LS补偿其容抗；发射端谐振网络除了将逆变器输出电压抬升至所需电压等级以外，同时确保该激励电压恒定；接收端谐振网络的作用是根据负载的需求向其提供恒定电压或电流，同时与耦合单元的等效内阻进行匹配从而获取高传输效率。本文中的“三阶”是指谐振网络由3个储能元件组成，并根据元件所在支路构成的形状可分为T型和Π型拓扑。

2 恒定输出型三阶谐振网络传输特性分析

谐振网络的传输特性决定了耦合机构的激励电压以及系统的输出电压/电流是否能保持恒定。为了得到具有恒定输出特性的电路形式，首先采用电路的传输参数矩阵推导了二端口网络输出恒定的一般性条件，结合此条件再分析T和Π型拓扑的传输矩阵，进而可得到元件参数的约束条件。

2.1 谐振网络输出恒定的一般性条件

谐振网络均可视为二端口网络，如图2所示。由于谐振元件采用高品质因数的电容或电感，因而在分析中元件的阻抗仅包含了电抗分量，电阻分量可忽略不计［16］。

图2 二端口网络示意图

网络的输入与输出的关系可通过传输参数矩阵表示为

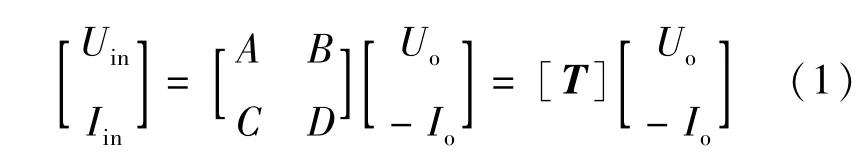
其中T为网络的传输参数矩阵。

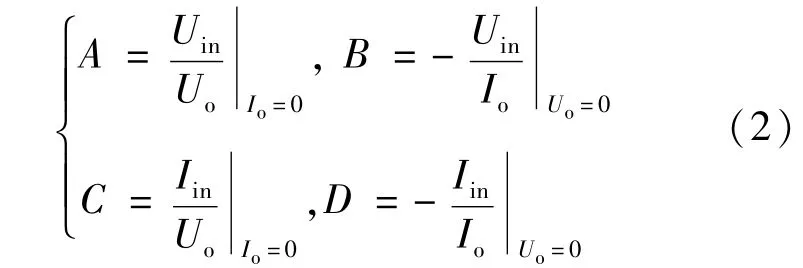
根据二端口网络输入电源及负载的需求，可将输入与输出关系分为4种模式：电压控电压（VCV），电压控电流（VCC），电流控电压（CCV），电流控电流（CCC），且对应模式下的输入输出增益函数可表示为

联立式和可得输入阻抗

网络具有恒定输出特性意味着输入输出增益函数不包含负载等效阻值Ro。据此可得到4种模式下网络增益函数的表达式及对应条件为

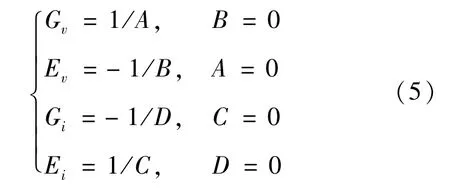
由于谐振元件的内部损耗往往可忽略，因而网络的传输效率可近似为1，即

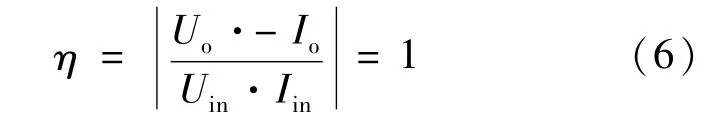
另外，由二端口网络的互易定理可知

联立式（2）（5）（6）（7），可得到4种模式下二端口网络输出恒定的传输参数矩阵为

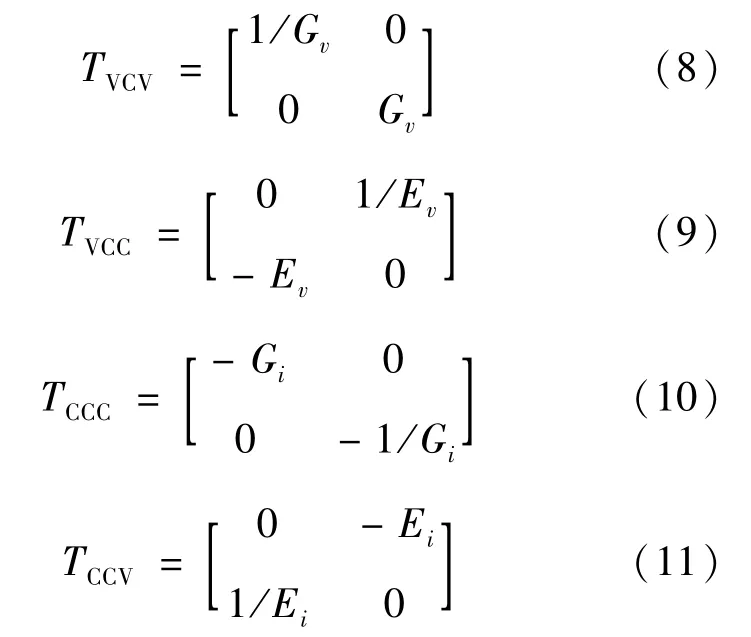
结合式（8）至（11）及式（4）进而得到4种模式下输出恒定时的输入阻抗为

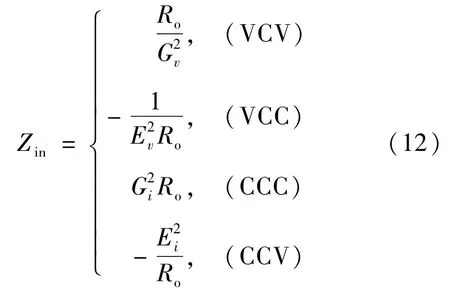
TVCV、TVCC、TCCC、TCCV表征了二端口网络在不同模式下输出恒定的一般性条件，结合式（5）即可分析三阶谐振网络的输入输出特性。

2.2 三阶T型谐振网络

根据元件所在支路共同构成的形状，三阶谐振网络可分为T型和Π型2种拓扑形式，如图3所示。

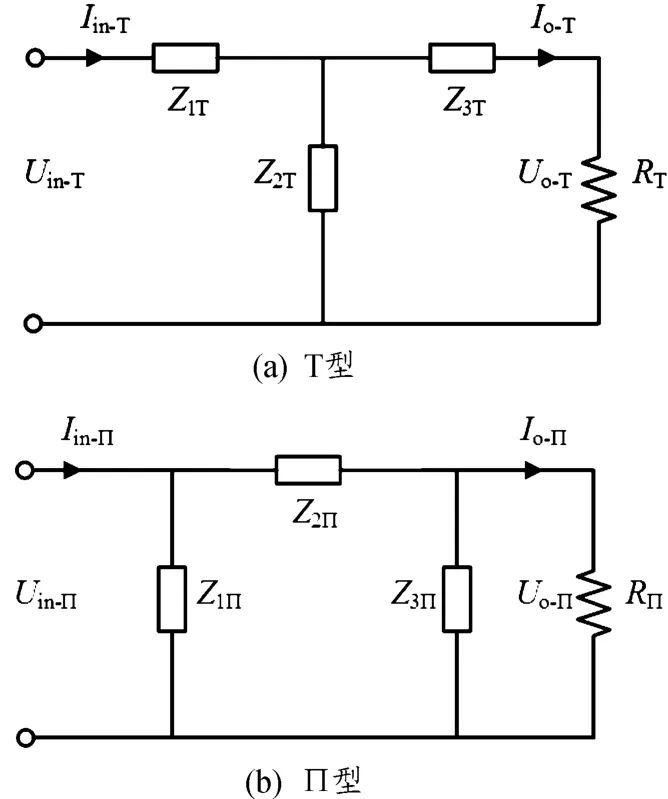
图3 三阶谐振网络电路图

通过分析对比T型谐振网络的传输矩阵是否满足二端口网络输出恒定的一般性条件，即可获得T网络能够实现的恒定输出模式，并依据二端口网络的特性可推导出恒定输出条件下T网络的输入阻抗及电压和电流增益。

由图3（a）及式（2）可得到T型谐振网络的传输矩阵为

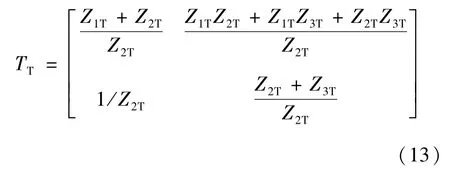
对比式（13）和（8）、（10）可知，由于Z2T≠0，传输矩阵TT并不满足VCV和CCC模式下输出恒定条件。而当元件满足条件

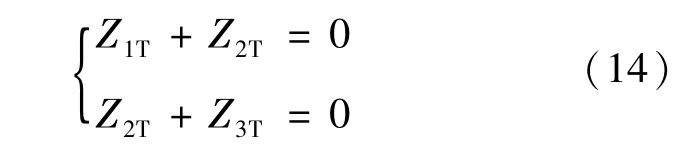
则T网络能够实现VCC和CCV模式下的恒流和恒压输出，且由式（5）可知2种模式的Ev和Ei分别为

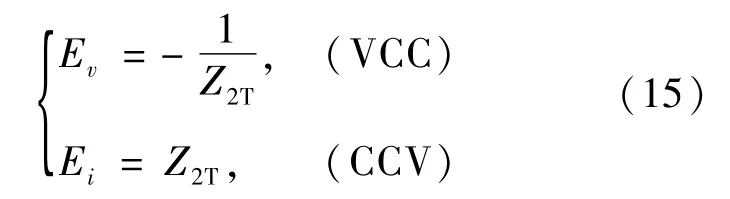
结合式（4）可推得输入阻抗分别为

进而可得到2种模式下的电流和电压增益为

其中QT为T谐振网络的品质因数，且

前述的式（14）表征了T网络在VCC和CCV模式下输出恒定的约束条件，据此可得到具有恒定输出特性的T型电路形式。式（14）表明T网络的元件1和元件2的阻抗幅值相等且相角差180°，而元件1和元件3的阻抗幅值和相角相同。这就决定了具有恒定输出特性的T型电路仅有2种形式：1）元件1和元件3均为电容，元件2为电感，即T-CLC电路，如图4（a）；2）元件1和元件3为电感，而元件2为电容，即T-LCL电路，如图4（b）。

图4 具有恒定输出特性的T型电路图

由图4（a）并结合式（14）可推导出2种电路形式在VCC和CCV模式下输出恒定的元件参数关系为

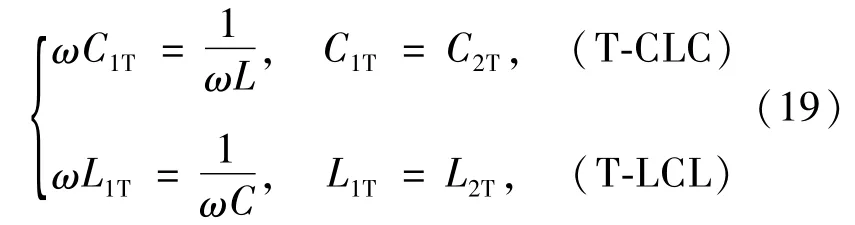
再由式（16）可得到2种电路的品质因数和输入阻抗为

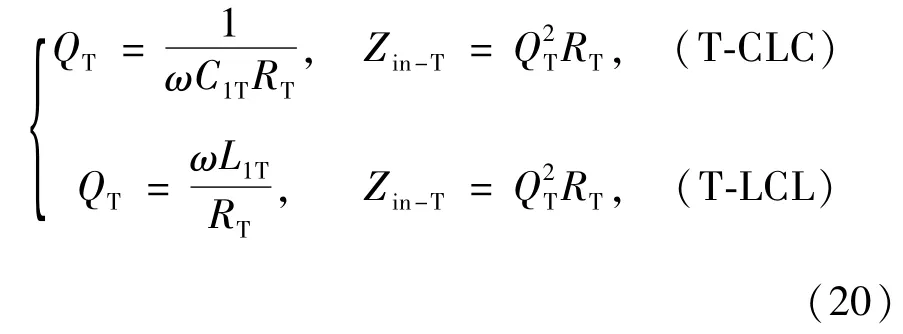
由式（20）可见，具有恒定输出特性的T网络的输入阻抗只包含电阻分量，且为等效负载阻值RT的QT2倍，因而T网络能够实现零输入相角运行状态，具有接近于1的功率因数。

联立式（17）和式（20），可计算出在VCC模式下2种电路的输出电流

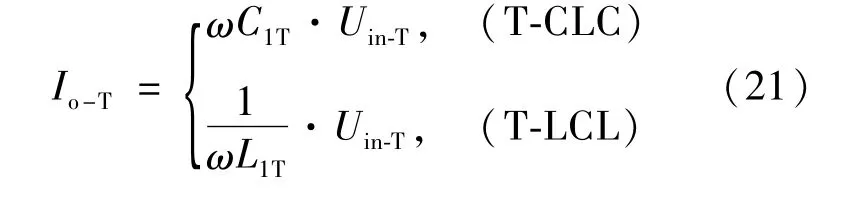
同理，可推得CCV模式下2种电路的输出电压

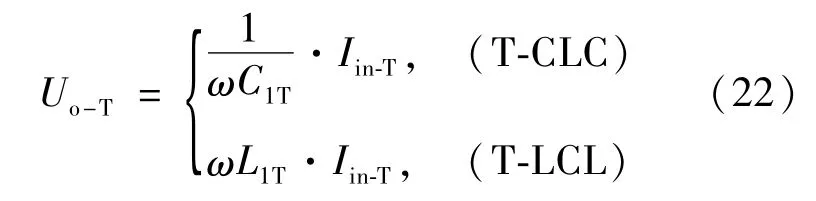
分析式（21）和式（22）发现，当T-CLC和TLCL电路处于VCC和CCV模式下的恒定输出状态时，只要输入电源保持恒定，电路的输出电压或电流只取决于其中谐振元件的取值而与负载等效阻值无关。

2.3 三阶Π型谐振网络

与T型谐振网络的分析类似，由图3（b）及式（2）可得到Π型谐振网络的传输矩阵为

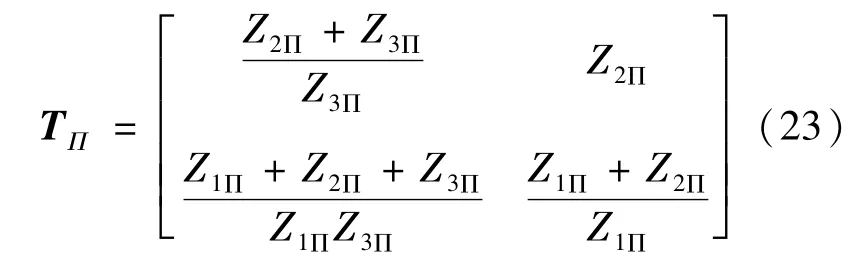
对比式（23）和式（8）（10）可知，由于Z2Π≠0，传输矩阵TΠ同样也不满足VCV和CCC模式下输出恒定的条件；而当Π网络的元件满足

则Π网络满足VCC和CCV模式下的恒定输出条件。对比式（24）和式（14）可知，Π型网络能够实现的2种恒定输出模式及其元件参数约束条件与T型网络一致，因而表明了具有恒定输出特性的Π型电路也有2种形式：Π-CLC和Π-LCL，如图5所示。

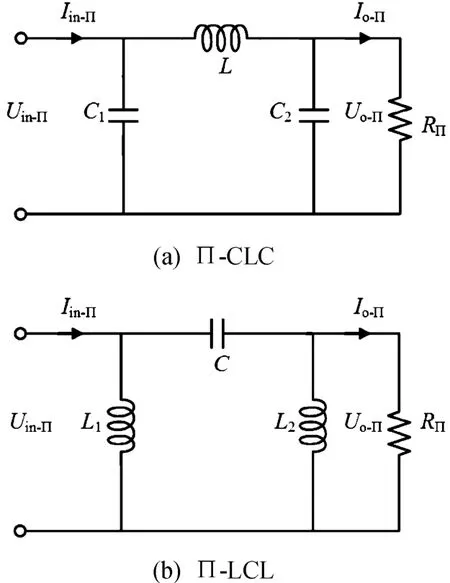
图5 具有恒定输出特性的Π型电路图

考虑到具有恒定输出特性的Π型网络与T网络存在相类似的约束条件，而且两者所采用的分析方法相同，所以省略了Π-CLC和Π-LCL电路传输特性的分析推导过程，相关参数见表1。

表1中的前3列给出了4种电路在恒定输出模式的输出电流或电压表达式，可见电路的输出仅由谐振元件决定；另外，从后4列可以看出谐振电路的品质因数关系到电路的输入阻抗和电压电流增益。

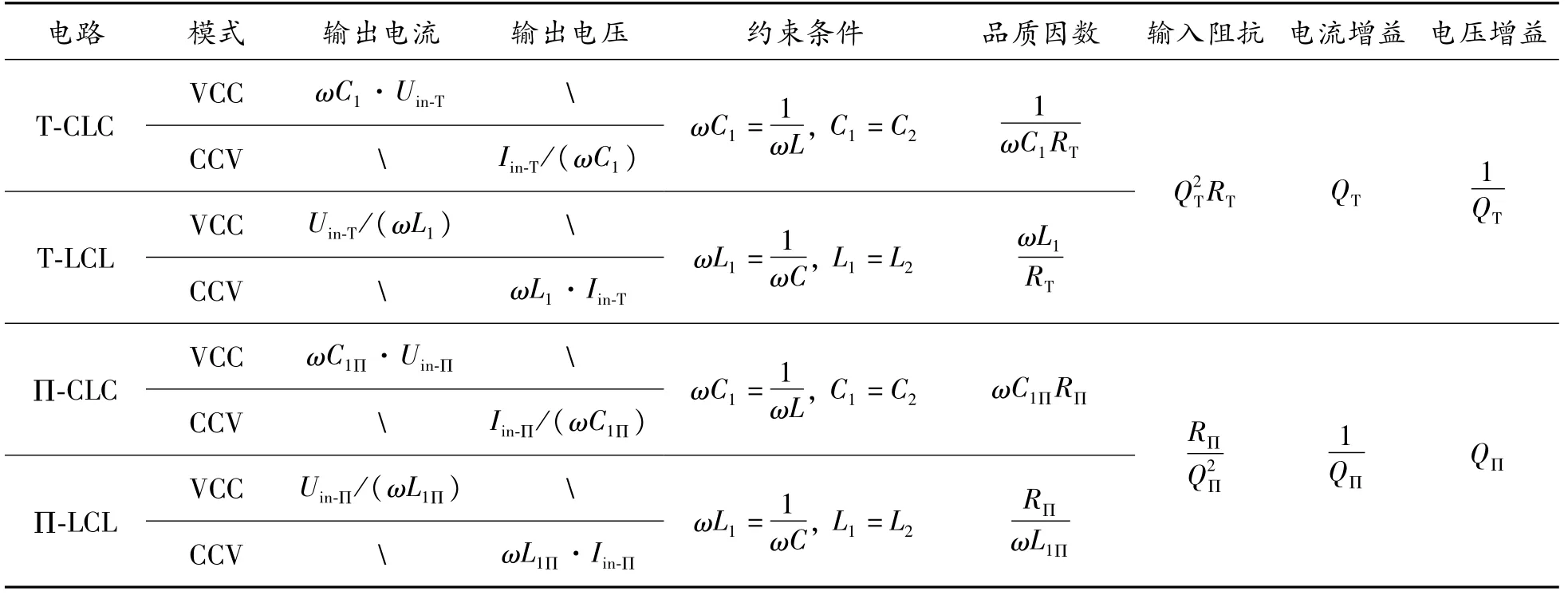
表1 T-CLC和T-LCL，Π-CLC和Π-LCL电路的传输特性参数

3 谐振网络的THD和参数敏感性分析

除了前述的谐振电路输出恒定的参数关系及传输特性参数以外，ECPT系统的设计还需考虑谐振电路的谐波畸变率THD和参数敏感性。因为逆变器输出所包含的谐波须经过抑制后才能进入后级的谐振电路及耦合单元，否则ECPT系统将会产生大量辐射干扰从而降低系统的电磁兼容性，同时还会影响逆变器的驱动控制电路稳定工作［14］；此外，实际中的元件参数及工作频率与理论值不可避免存在一定的偏差，如果此偏差引起谐振电路特性参数过大的变化，那么系统输出的稳定性将难以保证。

3.1 全谐波畸变率

根据THD的定义，当以电压方波作为输入时谐振电路的输入电流THD为

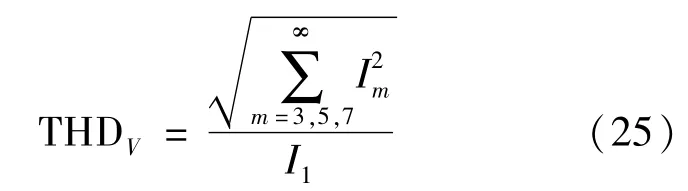
类似地，以电流方波作为输入时的输入电流THD则为

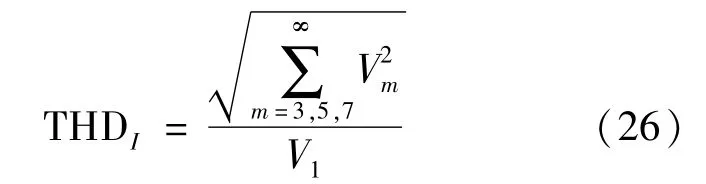
式（25）和（26）中的Im、I1、Vm、V1依次表示m次电流谐波、电流基波、m次电压谐波及电压基波。由于输入电压和电流方波均可展开成傅里叶级数，因而Im和Vm可计算为

进而可简化式（25）和（26）为

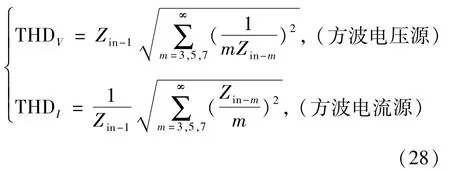
其中Zin-1、Zin-m分别为基波和m次谐波频率下谐振网络的输入阻抗。

对于T-CLC谐振电路，当按照式（19）的参数关系将电路配置在VCC模式时，根据其结构可得到

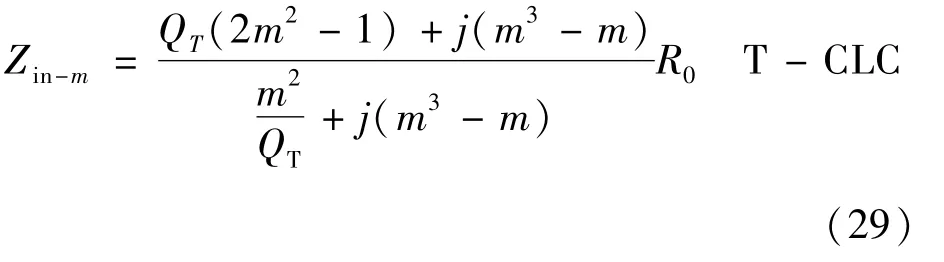
因而将式（29）代入式（28）可得到T-CLC电路在VCC和CCV 2种模式下THD的表达式

采用类似的方法可得到T-LCC、Π-CLC、ΠLCL 3种电路的THD，相关的表达式如表2所示，且表中的φ=m-1／m，χ=1-m2。由表2可看出，4种电路的THD仅取决于品质因数，进而可作出在VCC和CCV模式下4种电路的THD与品质因数的关系，如图6所示。

表2 T-CLC和T-LCL，Π-CLC和Π-LCL电路的THD

图6（a）表明T型电路在VCC恒流模式下若要获取较低的THDV，则要求其品质因数QT尽可能小。当QT＜1.5时，T-LCL电路的THDv＜20%，而T-CLC电路则要求QT＜0.7。这就意味着在相同谐波抑制能力的要求下，T-LCL电路的品质因数具有更大的选取区间。相反地，处于VCC模式下Π型电路的THDV则要求品质因数QΠ尽可能大，而且在相同品质因数条件下，Π-LCL电路比Π-CLC的THDv更低，具有更强的谐波抑制能力。

图6（b）表明在CCV恒压模式下T型CLC比LCL电路具有更强的抑制能力，而Π-CLC则相比于Π-LCL更强。需要特别指出的是，当Π型电路的品质因数小于0.45时，Π-CLC和Π-LCL 2种电路的THDI将趋于一致。

图6 4种电路在VCC和CCV模式下THD与Q的关系曲线

3.2 参数敏感性

谐振电路参数敏感性的分析主要是基于电路的输入阻抗特性与归一化频率及品质因数的相互影响规律［17］，因而本文首先推导了4种谐振电路的输入阻抗一般性表达式，进而分析归一化频率和品质因数对阻抗角的影响。

依据图4和图5可推导出T-CLC、T-LCL、ΠCLC及Π-LCL电路的输入阻抗为：

式中σT和σΠ分别为T网络和Π网络的电容比，λT和λΠ为网络中的电感比，ω为归一化频率，且满足

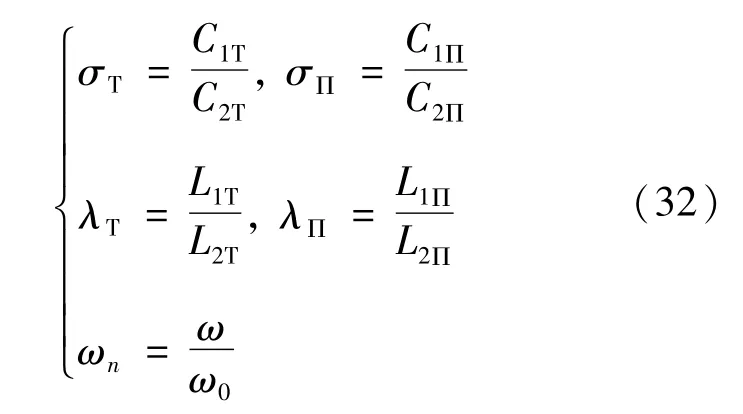
根据式中T-CLC电路的输入阻抗可作出以归一化频率和品质因数为自变量，阻抗角为因变量的等高图，且阻抗角采用角度单位，如图7所示。图中虚线为阻抗角为零时对应的ωn和Q，表明了当T-CLC电路处于谐振状态时，品质因数的变化不会影响网络的输入阻抗特性。从纵向来看，相同的品质因数情况下归一化频率增量和减量对阻抗角的影响具有对称性；从横向来看，Q处于0.7～3的范围内具有相对好的参数敏感性，而且当Q低于0.2时谐振网络将对频率的变化非常敏感。

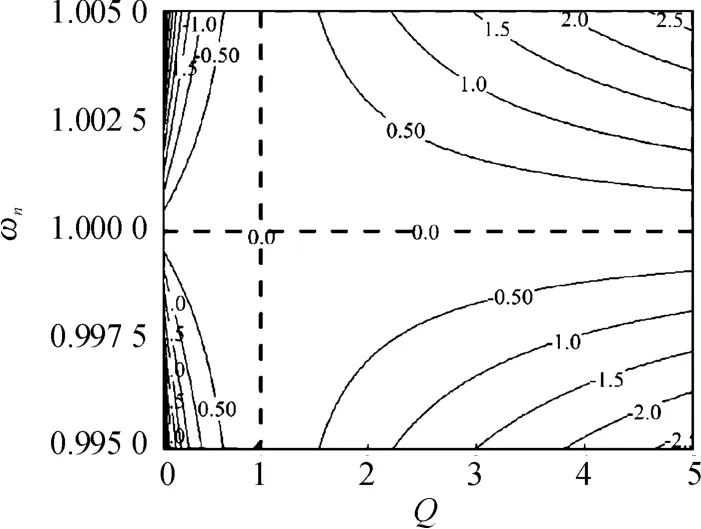
图7 T-CLC电路的输入阻抗角等高线图

类似地，可作出T-LCL、Π-CLC和Π-LCL的阻抗角等高图。因为T型网络和Π型网络结构上的对称性，使得这3种电路的等高图与图7基本相同。

通过对谐振网络THD和参数敏感性的分析，并结合其传输特性，可得到电路输出增益、THD和敏感性对品质因数的要求，如表3所示。其中符号“↑”表示尽可能大，符号“↓”表示尽可能小。可以看到，电路输出增益和THD对品质因数的要求相反。以T-CLC为例，较大的输出电流要求品质因数QT尽可能大，而较低THD则要求QT尽可能小。因而在实际的参数设计中需要结合输出增益、THD和参数敏感性3个方面，折中选择谐振电路的品质因数。进而可以得到具有恒定电压及电流输出的ECPT系统结构，如表4所示。其中恒压型ECPT的发射端和接收端谐振电路分别处于VCC和CCV模式，而恒流型系统则工作在CCVVCC模式。

表3 T-CLC和T-LCL，Π-CLC和Π-LCL电路的增益、THD和参数敏感性对品质因数的要求

表4 恒压型及恒流型ECPT电路系统结构

通过分析表4发现，恒压型及恒流型电路结构中THD和参数敏感性是相互矛盾的特性。以发射端采用T-LCL形式而接收端采用Π-CLC结构为例，此种系统电路结构具有相对更小的THD，然而参数的敏感性也相对更高。这就意味着系统虽然具有更好的电磁兼容性，但同时也对驱动电路和元件参数的精度提出了更高的要求，因而系统的电路结构的选择需要在THD和参数敏感性之间折中考虑。

4 系统参数设计方法

基于谐振电路传输特性、THD及参数敏感性的分析结果，可以分别得到系统的参数设计方法，其设计流程主要包含4个部分：系统电路结构的选择、耦合机构及补偿电感的确定、接收端及发射端谐振电路的设计，如图8所示。

首先给定系统需求的输出电压或电流及等效的负载阻值，再根据系统输出特性的要求由表4选择系统的电路结构，基于工程经验确定系统的工作频率，选择等效电容Cs尽可能大的耦合机构，并依据补偿关系ω2CsLs=1计算出补偿电感LS；进一步选择接收端谐振电路的品质因数，并由表2和图7分析计算THD和参数敏感性是否满足要求，如若不满足则调整品质因数或采用其他谐振电路形式，进而由表1中的参数约束关系计算出接收端谐振元件的参数值；采用类似的方法设计出发射端谐振电路的元件参数，最后利用发射端谐振电路的输入输出增益获得输入直流电源的有效值。

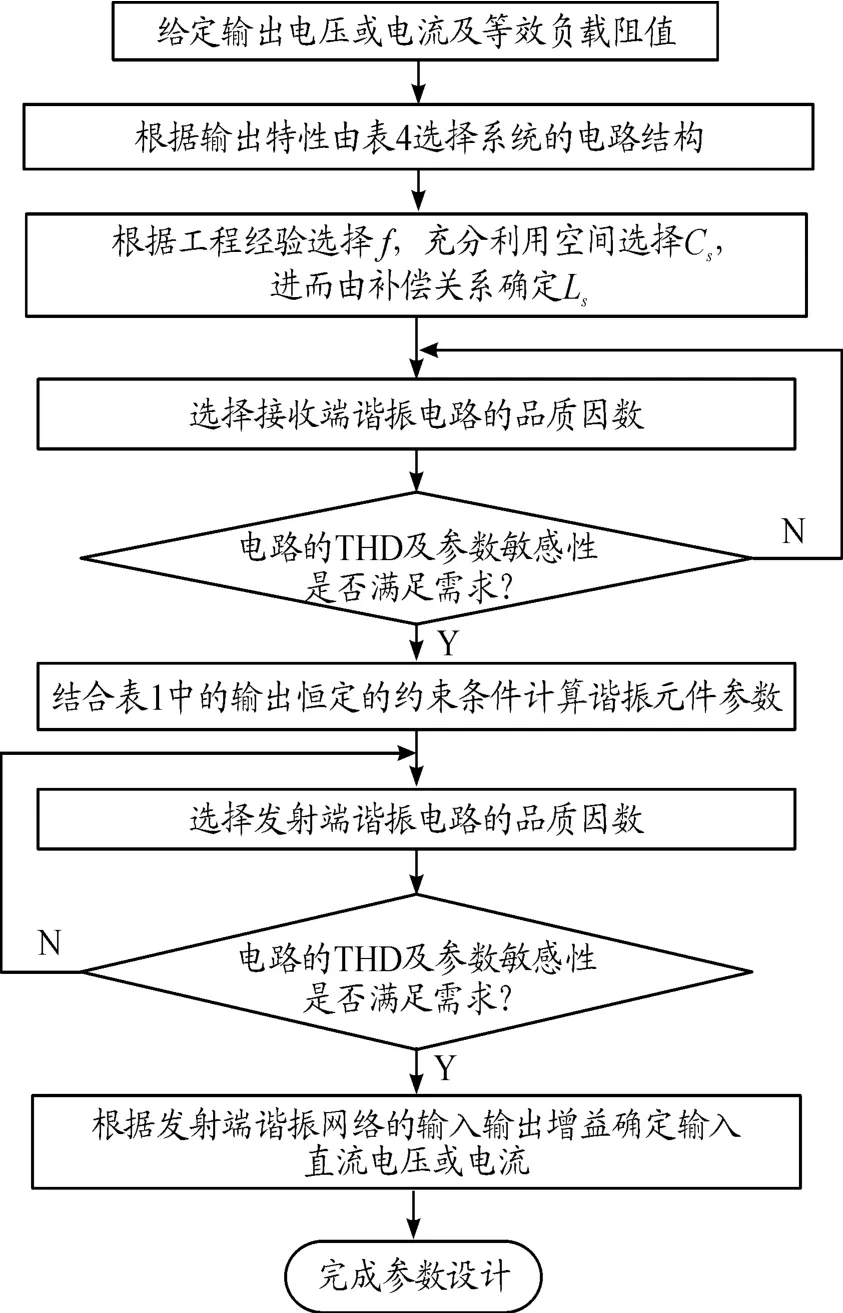
图8 系统参数设计流程框图

5 仿真与实验验证

为了验证基于三阶谐振网络ECPT系统的传输特性及参数设计方法，以基于T-LCL和Π-CLC的恒压型系统为例，如图9所示，在Matlab中建立仿真电路并搭建了实验样机系统。

图9 基于T-LCL和Π-CLC谐振电路的ECPT系统电流结构电路图

参照图8，首先给定了系统的输出特性及性能要求，输出电压100 V、等效负载阻值100Ω，发射端谐振电路输入电流THDT＜10%，接收端谐振网络输出电压的THDΠ＜10%，并由工程经验设定耦合电容Cs=350 pF，工作频率f=500 kH。综合考虑谐振电路输出增益、THD和参数敏感性，结合表3选择T-LCL和Π-CLC电路的品质因数分别为QT=0.37，QΠ=1.25，进而依据表1中恒定输出的参数约束条件计算出谐振元件的参数。最后根据傅里叶变换和T-LCL的输出增益可得直流输入电压为式（33）。据此获得输入电压为38 V，系统的主要参数如表5所示。

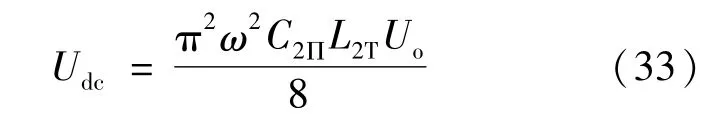
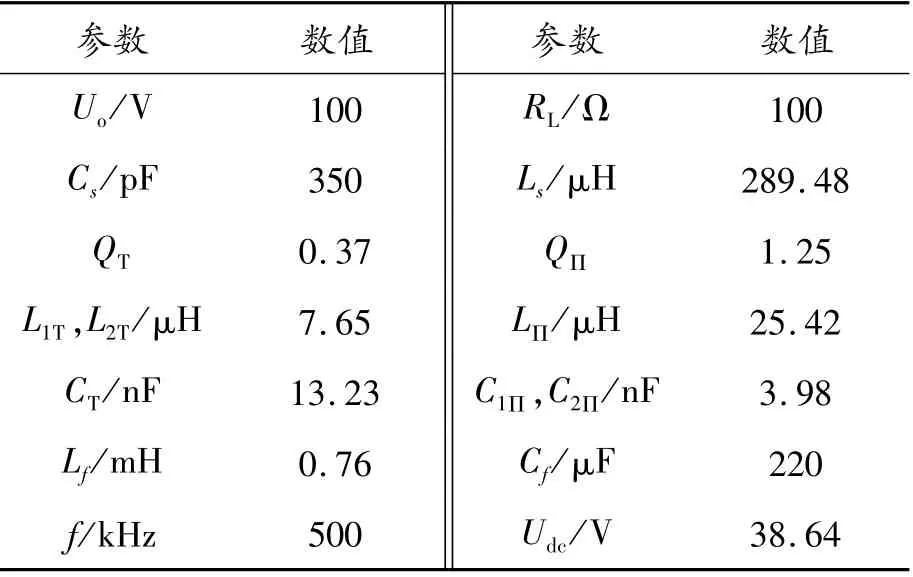
表5 系统主要参数

图10为系统输出电压的仿真波形，反映了负载等效电阻变化与输出电压的关系。系统的运行分为3个时段：在时段1中RL=100，在时段2中RL由100Ω减小为90Ω，在时段3中RL增加至110Ω，每个时段的输出电压依次为98.5、98.2、98.5 V。这就说明了负载的变化引起的输出电压变化仅在0.3 V左右，进而验证了系统的输出电压不会随着负载等效阻值的变化而改变。需要说明的是3个时段输出电压与设定值100 V均存在偏差的主要原因是发射端注入的谐波。

图10 输出电压仿真波形

图11和图12分别为时段1中逆变器和整流桥输出电压及电流的仿真波形，反映了T-LCL和Π-CLC电路对谐波的抑制能力。通过MATLAB中的FFT工具箱可测得图11中逆变电流Iinv的THD为5.7%，该数值与据表2获取的理论值5.76%基本吻合。采用相同的方法可测得时段2和时段3中Iinv的THD为5.2%和5.7%，该数值同样与理论值基本一致，也满足性能要求THD＜10%。类似的，可测得整流桥输出电压在3个时段的THD依次为8.7%、9.6%和8.7%，该结果同样与理论值相吻合。这就验证了三阶谐振电路的THD分析结果的正确性。

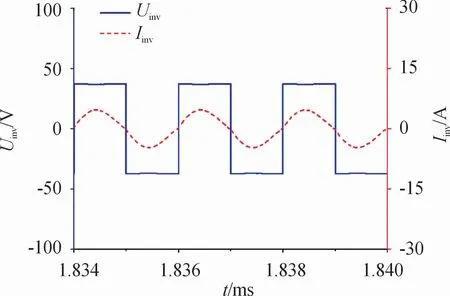
图11 时段1中逆变器的输出电压和电流仿真波形

图12 时段1中整流桥的输出电压和电流波形

图13为所搭建的样机系统装置，其元件的参数与仿真参数相同，主要器件的型号如表6所示。

图13 实验样机系统装置

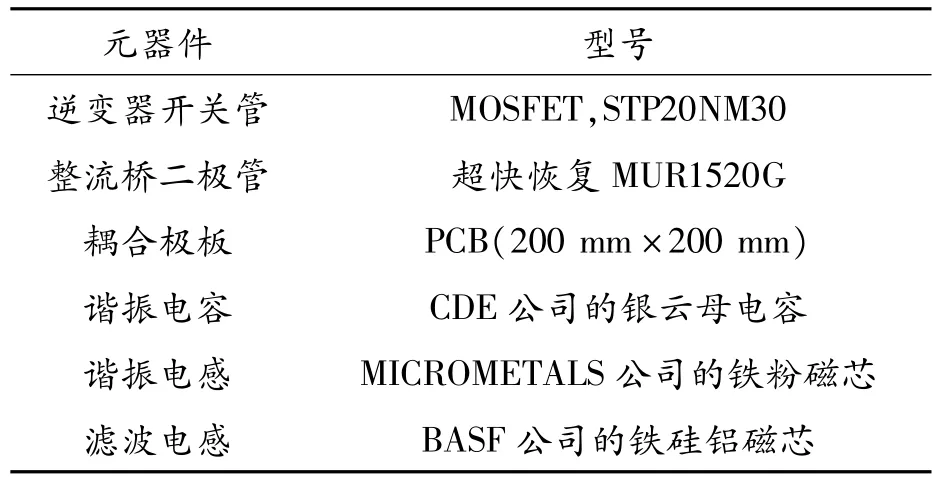
表6 样机系统主要元器件的型号

样机中的谐振电容采用了具有高Q值的银云母电容，而谐振电感则绕制在低高频损耗的铁粉磁芯中，耦合极板为敷制在PCB板上的铜箔。

图14（a）和（b）分别为负载等效电阻由100Ω增加到110、100Ω减小至90Ω2种情况下样机系统的输出电压波形。负载切换以前输出电压为100 V，切换以后输出电压首先出现±5 V左右的波动，再重新稳定到100 V左右。这说明负载阻值出现±10%的变化但基本不会影响到系统的输出电压，从而进一步验证了系统的恒定输出特性。图14（c）为逆变器和整流桥的输出和输入波形，可以看到样机的实验波形与图11及图12中的仿真波形基本一致，进而验证系统参数设计方法的可行性。所搭建的样机系统能以整机效率83%输出接近100 W 的功率，且耦合结构的传输效率不低于90%。

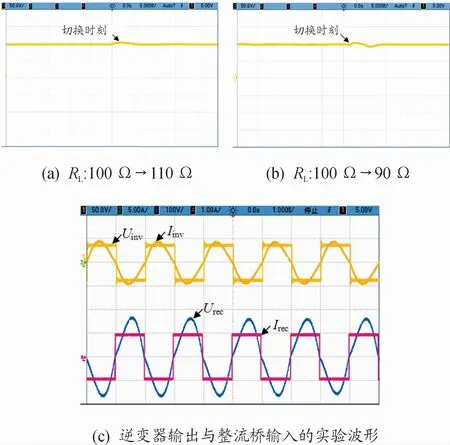
图14 实验波形

6 结论

本文给出了二端口网络输出恒定的一般性条件，分析了三阶谐振网络的传输特性并确定了具有恒压及恒流输出特性的T型和Π型电路形式，据此建立了恒压及恒流模式下对应的4种系统电路结构，并提出了系统的参数设计方法。仿真及实验结果表明所提出的系统结构不仅具有恒定输出特性，同时还兼具较好的谐波抑制能力和参数鲁棒性。所给出的恒压型及恒流型电路结构及其设计方法为实际中ECPT系统的拓扑结构的选择及设计提供了理论依据和分析方法。另外，本文仅围绕三阶谐振网络展开了分析，目前国内外的学者逐渐开始关注四阶谐振网络的传输特性，针对基于四阶网络的恒定输出型ECPT系统的研究将会在本文的后续内容中展开。