阶次跟踪在行星齿轮箱非平稳信号故障诊断中的应用
2021-03-22赵东平
王 博,王 斌,赵东平
(1.西安航空学院 飞行器学院,西安 710077;2.西安陕鼓动力股份有限公司,西安 710075)
风力发电机机组因其频繁低速启动、转速时刻随风速在变化,导致齿轮箱行星轮系在传动的过程中受到交变载荷的冲击,故齿轮箱行星轮系成为故障的高发区。对齿轮箱行星轮系进行状态监测及故障诊断,对提高发电效率以及降低因故障维修的停机时间具有非常重要的经济意义。
齿轮箱行星轮系因传动比大、承载高等特性,已成为齿轮箱中不可或缺的关键环节。振动加速度传感器拾取的齿轮箱行星轮系振动信号也是复杂的复合信号。一是齿轮箱行星轮系运行在时变工况下,导致壳体上拾取的振动信号是非平稳的[1-3];二是多路径的传递特点,导致传感器拾取的振动信号是多路径调制的。若采用传统的傅里叶变换对齿轮箱行星轮系拾取的振动信号进行频谱分析,频谱中会出现“模糊”现象[4],不能准确识别故障特征频率。
目前,国内外对于风电齿轮箱行星轮系的故障诊断的研究主要集中在平稳状态下,对于时变工况下齿轮箱行星轮系的故障诊断方法研究很少,且主要是对信号的时域和频域进行处理[5],阶次分析在风电齿轮箱行星轮系故障诊断中的研究极少。
本研究利用阶次分析技术,解决了传统频谱分析在时变工况下的缺陷,对风电齿轮箱行星轮系进行了故障诊断。
1 计算阶次跟踪分析法
阶次跟踪分析方法在低速重载时变工况下故障诊断的优越性是不言而喻的[6],其剔除了转速对频谱的影响,在阶次谱图中可以及早辨识故障特征频率并进行精确定位。此时需要把齿轮箱行星轮系齿轮出现损伤时的故障特征频率换算到阶次谱上所对应的阶次,此阶次与齿轮损伤时故障频率是等同的,即不同阶次对应不同部件损伤,同一部件的故障阶次是一定的,阶次不会随转速的变化而变化。
阶次、频率、转速之间的关系为
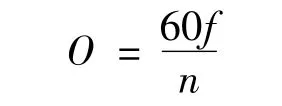
式中:O为观测对象的阶次;f为观测对象的频率;n为参考轴的转速。
阶次跟踪的实质是对参考轴等角度重采样,其实现方法有硬件、软件两种[7-12]。本研究通过计算阶次跟踪法,利用振动加速度传感器和转速传感器同步采集信号,再通过数值积分将转速-时间曲线转换为转角-时间曲线,并进行等角度重新采样,即可将振动信号变成角域平稳信号,最后对角域信号进行傅里叶变换,得到阶次谱。
2 振动信号模型
齿轮箱行星轮系由太阳轮、行星轮、内齿圈和行星架等关键部件组成,其中内齿圈固定,行星轮在自传的同时还绕太阳轮公转。在齿轮啮合过程中,参与啮合齿数的交替变化引起啮合刚度的周期变化,从而引起啮合振动。当局部损伤的轮齿与其他轮齿啮合时会产生冲击现象。在齿轮箱的周期性旋转啮合中,冲击会按照一定的时间间隔重复性出现,此冲击会对啮合振动产生调幅和调频作用。借鉴冯志鹏等[13]研究齿轮箱行星轮系振动信号的模型,可得到稳态工况下的振动信号模型:
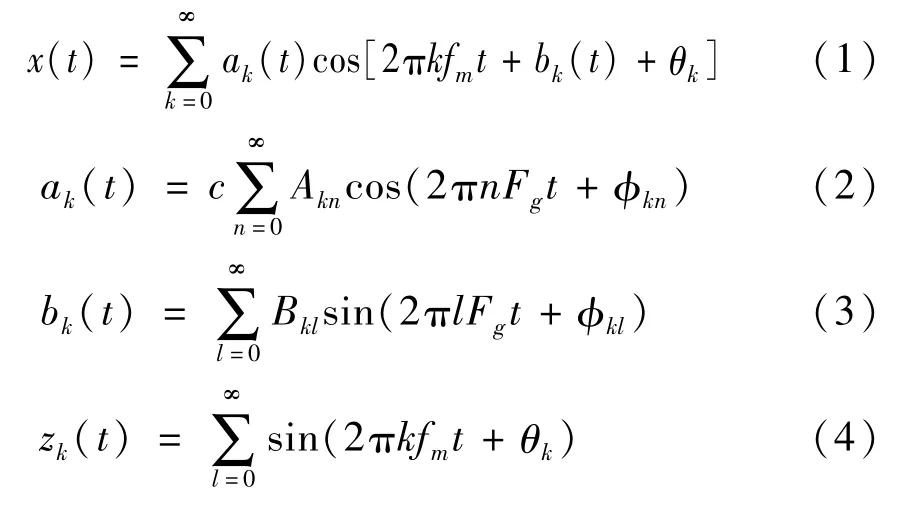
其中:ak(t)、bk(t)分别为信号的调幅和调频函数;zk(t)为载波信号;Akn和Bkl分别为太阳轮、行星轮和内齿圈的局部故障引起的调幅和调频强度;c为常数;fm为行星轮系的啮合频率;Fg为局部故障频率,其包括太阳轮、行星轮和内齿圈的局部故障频率;θk、φkn、φkl为初始相位。
在变转速工况下,其相位为
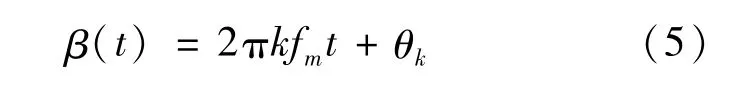
将载波信号进行微分计算,可求得时变的啮合频率:
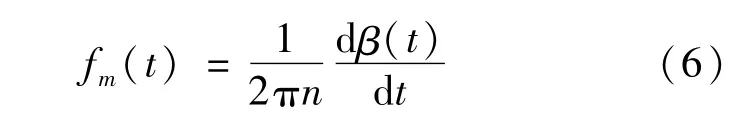
因此可得时变工况下的载波信号:
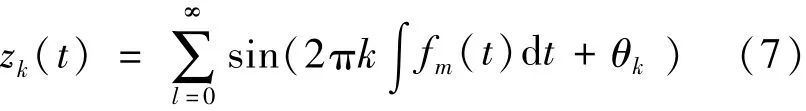
对式(1)~(3)进行简化,只考虑基频,即啮合频率和故障频率,模型简化为
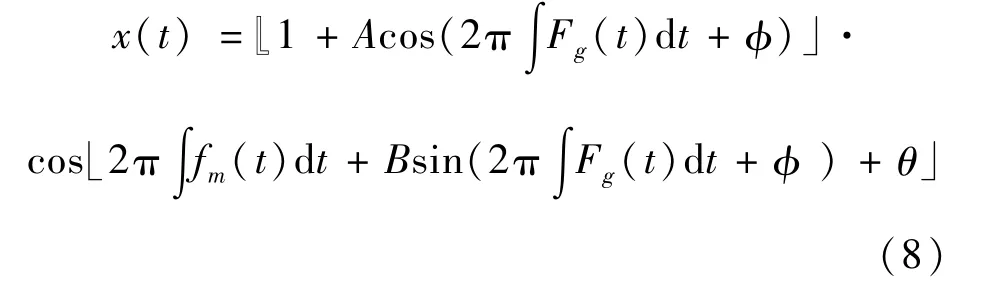
根据Bessel函数可以得出[14]:
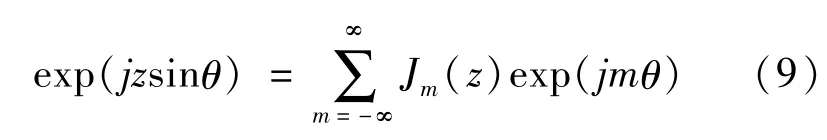
进而可以得出式(8)的傅里叶变换:
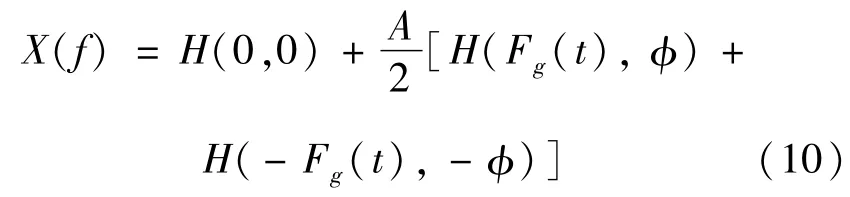
其中,中间函数:
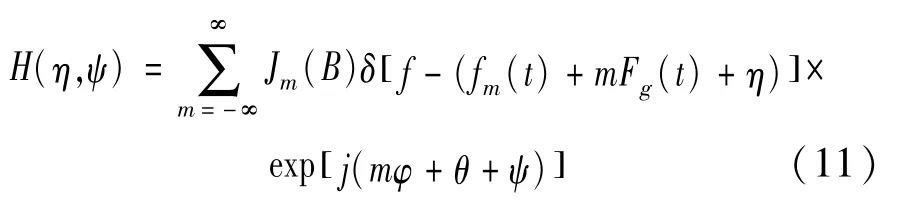
由式(10)、(11)可见,在啮合频率两侧会调制边频带,边频带出现在fm(t)+mFg(t)位置处,m取值从(-∞,∞)范围内的整数。若考虑啮合频率的倍频kfm(t)作为载波的情况,则边频带会出现在kfm(t)+mFg(t)位置处,啮合频率两侧边频带间隔均为局部故障齿轮的故障频率Fg(t)。
3 行星轮系故障特征阶次
行星齿轮箱的结构决定了振动信号的复杂性。当行星轮系的内齿圈、行星轮、太阳轮出现局部故障时,齿轮在啮合过程中就会定期的撞击损伤点,加之振动信号的调幅调频作用,频谱必然会出现“模糊”现象。通过计算阶次跟踪方法,可以消除转速的影响,故障部件的故障阶次是固定不变的,找到不同部件的故障阶次,就可以精确对故障进行定位。
当行星架为输入端时,设zs、zp、zr分别为太阳轮、行星轮、内齿圈齿数;nh为行星架转速;fh为行星架转频。故行星轮系的转速及啮合频率为:
太阳轮的转速为
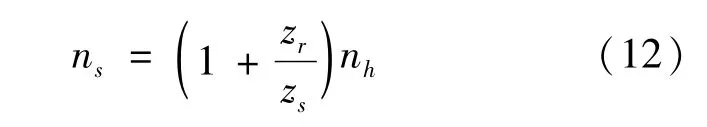
行星轮的自转转速为
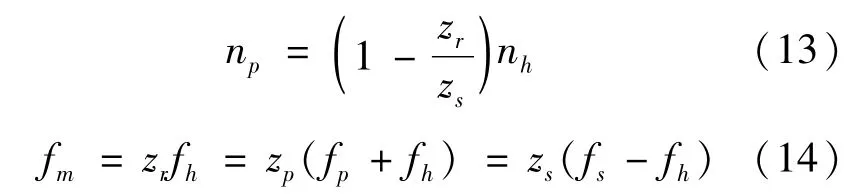
当太阳轮出现局部故障时,在太阳轮旋转一圈的过程中,会与每个行星轮都产生啮合状态,所以太阳轮的故障频率与行星轮个数有关,其故障频率为

行星轮局部故障频率为

当内齿圈出现局部故障时,在行星架旋转一圈的过程中,会与每个行星轮都产生啮合状态,所以内齿圈的故障频率与行星轮个数有关,其故障频率为

式中N为行星轮个数。
通过以上计算,可以得到齿轮箱行星轮系太阳轮、内齿圈、行星轮故障特征频率以及对应的阶次,如表1所示。

表1 行星轮系故障频率及对应阶次
在实际测试中,只需知道行星轮系太阳轮齿数、内齿圈齿数、行星轮的齿数和行星轮的个数,以及参考轴的阶次Oh,本文参考轴以齿轮箱行星架的阶次为参考轴,则可计算出各个部件的故障阶次。
由表1可看出:齿轮箱各部件的故障频率是随着齿轮箱行星架转频而时刻变化,而各部件的故障阶次却是恒定不变的,只与参考轴的阶次有关,一旦参考轴的阶次确定,则各部件的故障阶次随之确定;在啮合阶次旁边会调制故障部件的故障阶次。
4 测试信号分析
测试对象为某风场的1.5 MW 风力发电机组齿轮箱二级行星轮系。齿轮箱的结构为两级行星轮系加一级平行传动,行星轮有3个,齿轮箱行星轮系的齿轮的步数见表2,本次以齿轮箱输入轴的阶次Oh为参考阶次,各个部件的故障阶次通过输入轴的阶次Oh计算得到。转速传感器安装在齿轮箱输出端,即输出轴阶次为1,根据行星轮系参数和三级参数可计算出二级传动比为5.25,三级传动比为3.57,根据齿轮箱传动比计算出齿轮箱输入轴阶次Oh,从而计算出行星轮系各个部件的故障阶次,如表3所示。本次所使用的振动加速度传感器灵敏度系数为500 mV/g,以及数据采集单元和计算机。振动加速度传感器的安装在内齿圈径向水平位置。所有采集的振动信号都在接近额定转速1 800 r/min附近所采集的数据。

表2 行星轮系齿轮的步数
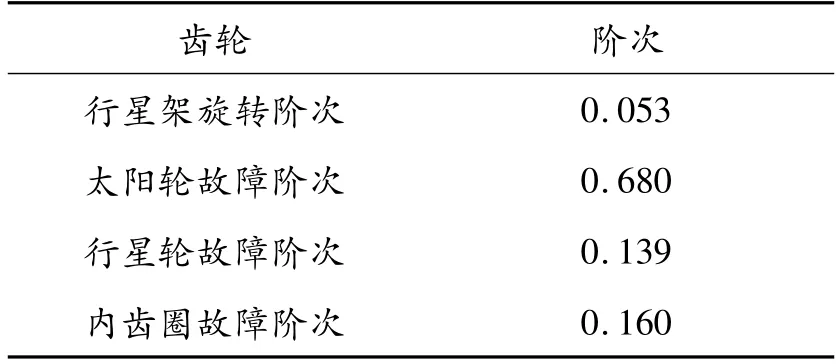
表3 行星轮系单一缺陷阶次
当各部件的故障阶次计算好后,在分析所采集的振动数据时,就可以分析啮合阶次旁边调制的边频带,然后根据边频带值的大小,参照表3找出故障齿轮,对故障进行定位。
安装好传感器、线缆和布置好数据采集器以后,设置好信号采集参数,如表4所示。由采样频率可得分析频率为1 000 Hz,参考轴转频为30 Hz,即为1阶次。这样阶次取30阶可满足分析要求。

表4 采集信号参数
在采样时长50 s内,可以看到转速波动很明显,转速的波动是由于风速变化引起的,如图1所示。
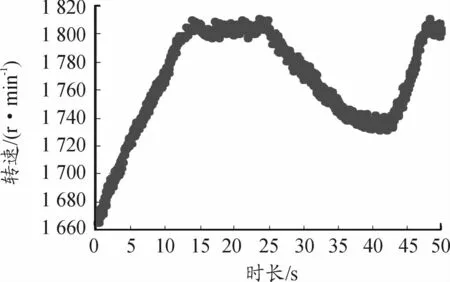
图1 无故障时采集的转速波形图
图2为采集的无故障时振动加速度时域波形图,时域波形图未发现明显的冲击振动。图3是对图2振动加速度时域波形直接作傅里叶变换得到的频谱图,因转速波动的影响,在齿轮啮合频率fm(160 Hz)、2fm(320 Hz)、3fm(480 Hz)等多倍频的两侧,频谱图呈现“模糊”现象,不能有效识别啮合频率旁边调制的边频带kfm+mFg。这时把时域等间隔采样转换成角度域等角度采样,那么信号就变换成角度域的平稳信号,如图4所示,然后再对其进行傅里叶变换,就得到阶次谱,如图5所示。
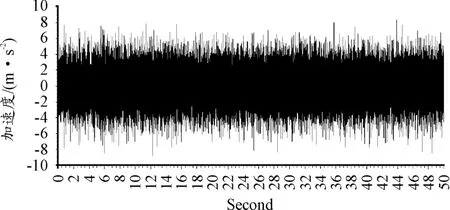
图2 无故障振动加速度时域波形
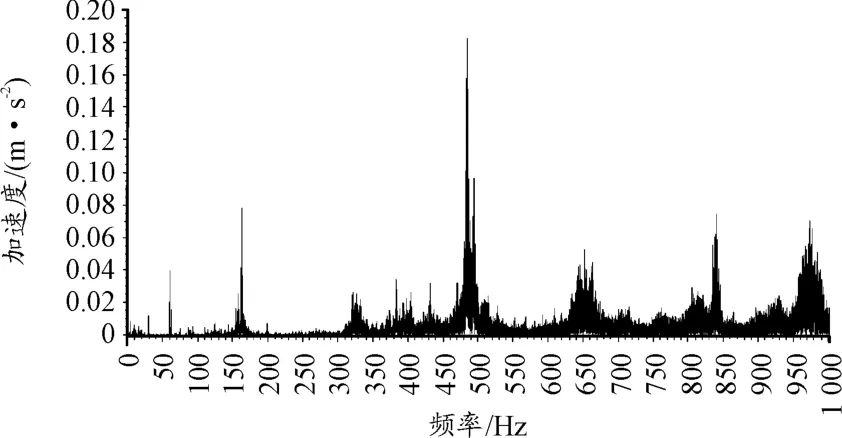
图3 无故障振动加速度频谱图
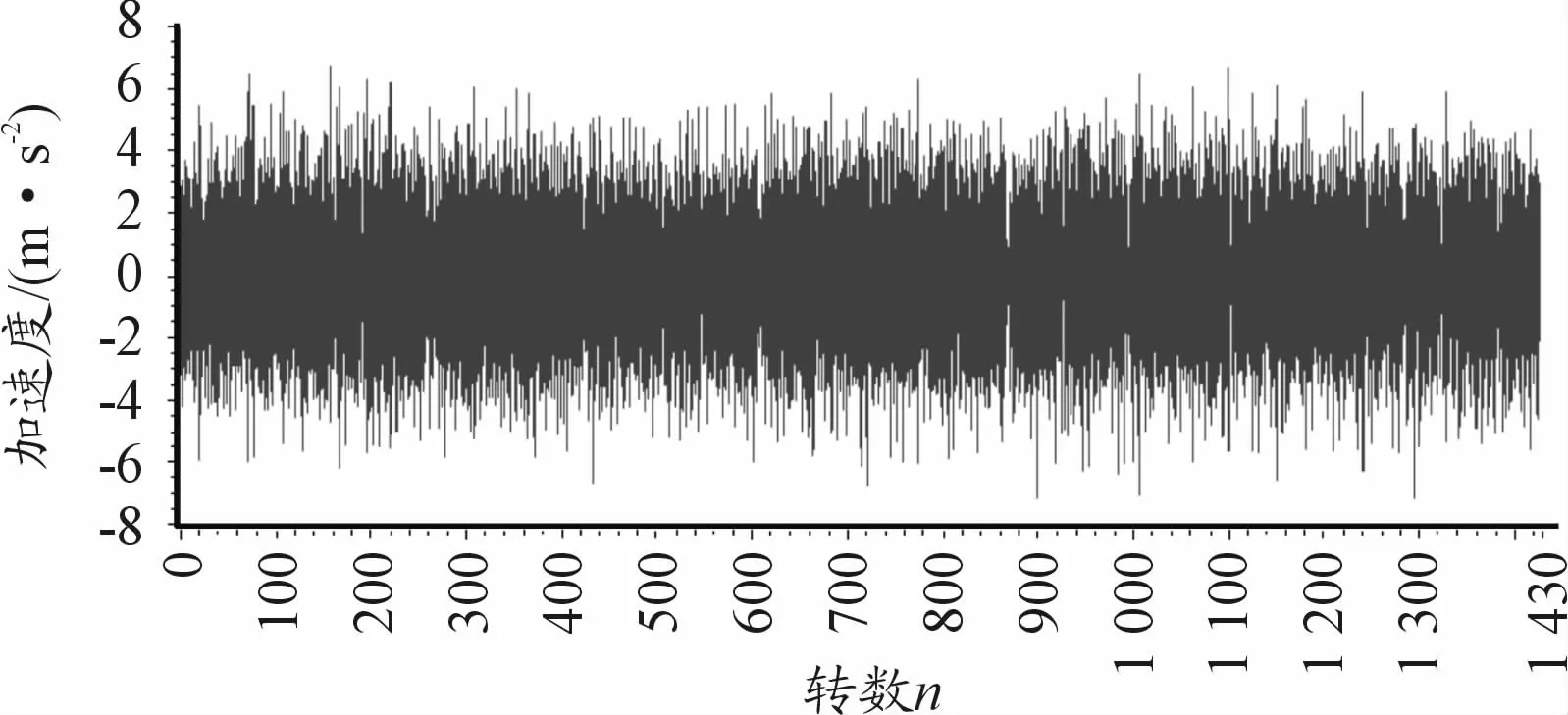
图4 无故障振动加速度阶次波形图(角域信号)
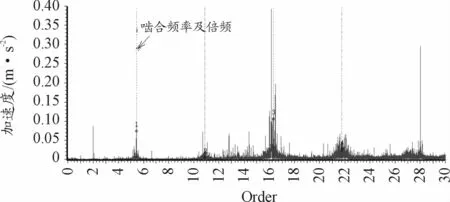
图5 无故障振动加速度阶次谱图
从图5和图3的对比来看,在阶次谱上,在齿轮啮 合 阶 次 fmo(5.406)、2fmo(10.812)、3fmo(16.218)等多倍频的两侧调制数量少的内齿圈边频带Or。阶次谱清晰的识别啮合阶次两侧调制的边频带kfm+mFgo,可以及早发现齿面损伤,减少意外停机时间。
随着机组运行时间的增加,故障也会逐渐发生,在同等的条件下对采集的振动数据进行分析。这一次采集的转速波动情况如图6,可以看出转速存在明显波动。
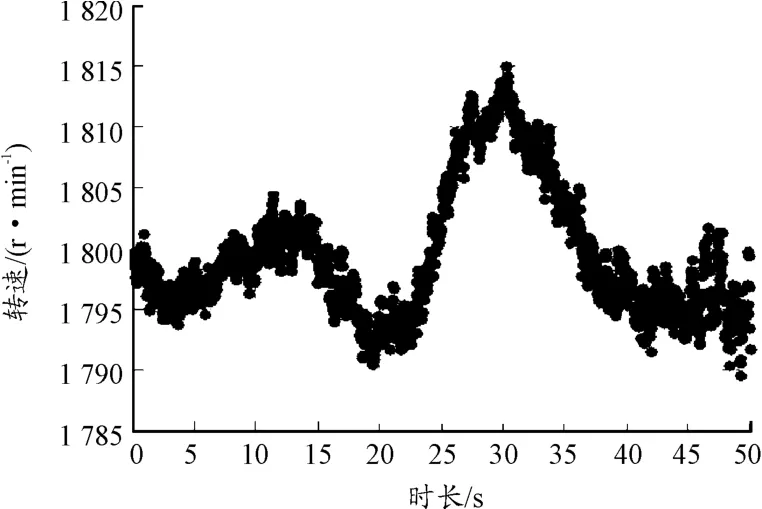
图6 故障时采集的转速波形
从时域波形图来看,已经出现比较明显的等间隔冲击,间隔时间0.208 s,由此可知冲击频率为4.8 Hz,接近内齿圈故障频率Fr,如图7、8所示。
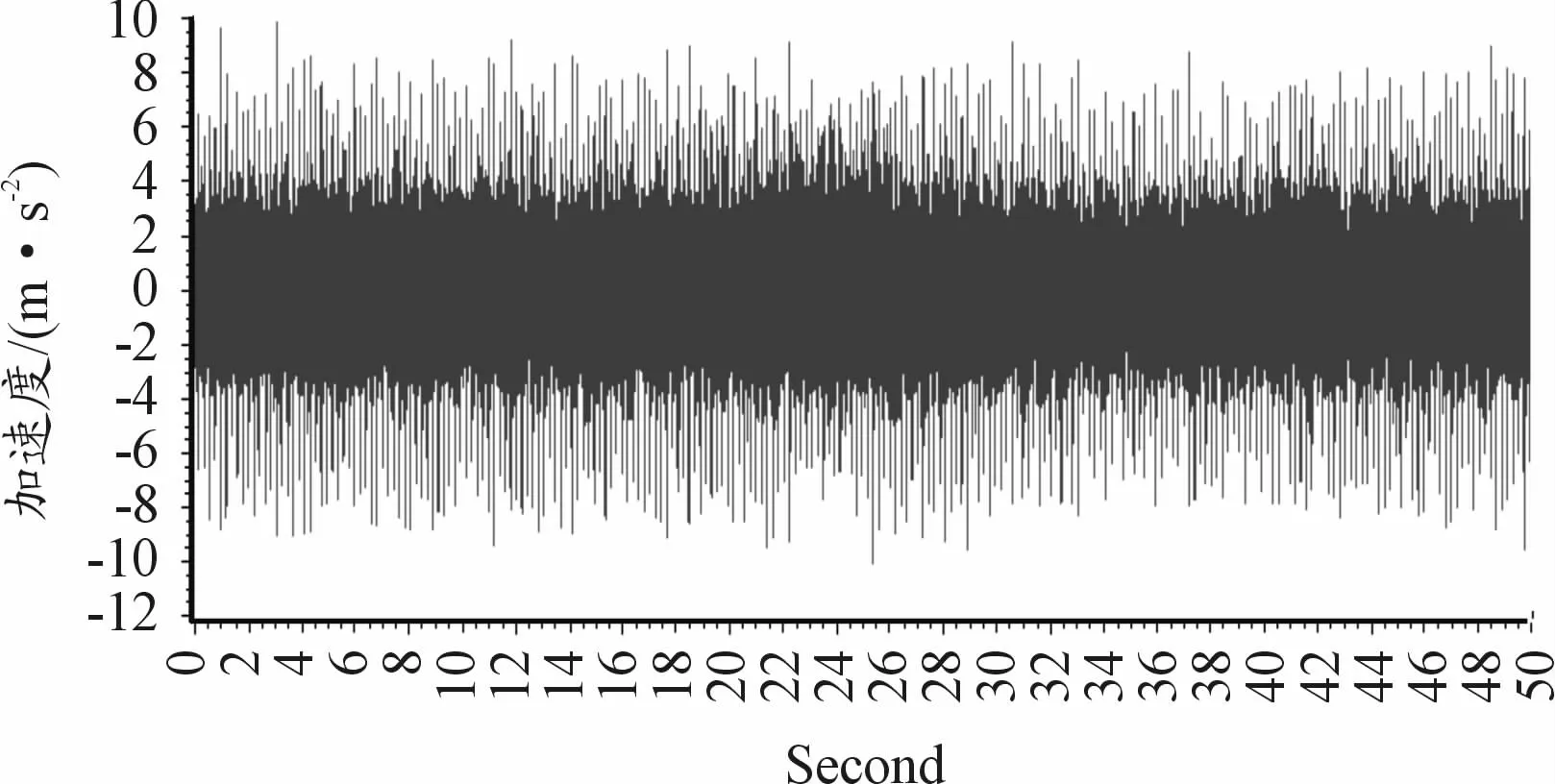
图7 故障时振动加速度时域波形
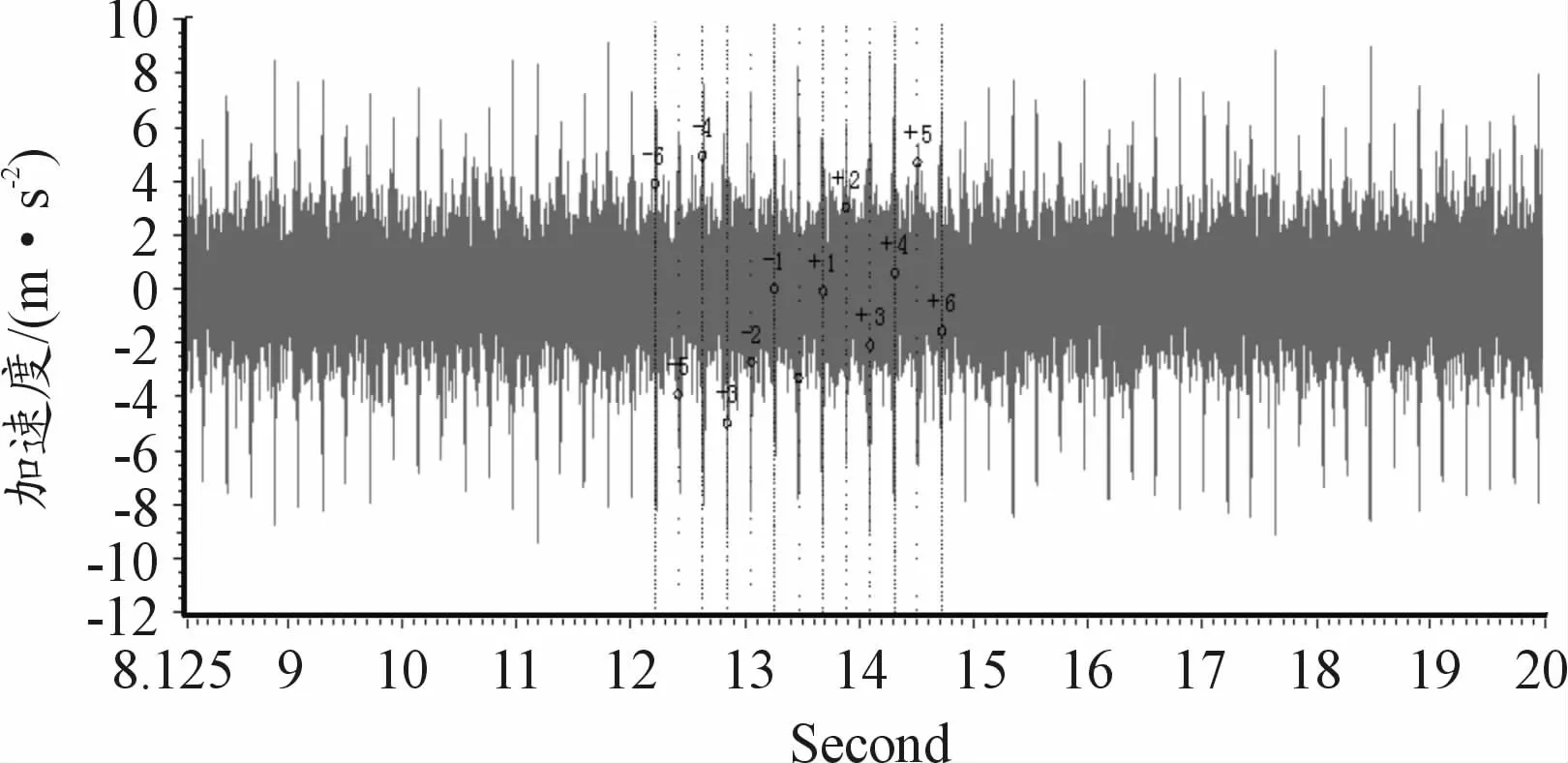
图8 故障振动加速度时域波形放大图(图7细节)
图9为图7时域波形对应的频谱图,可以看出,由于转速波动的影响,不能有效识别啮合频率kfm旁边调制的边频带kfm+mFg。此时把信号从时域波形非平稳信号变换到角域平稳信号,其信号的阶次波形如图10、11,从阶次波形可以看到等间隔的冲击,冲击间隔为0.160阶次。然后再对角度域平稳信号进行傅里叶变换,得到平稳信号的阶次谱,如图12、13所示,在阶次谱上,啮合阶次及其倍频kfmo占主导能量,且在啮合阶次的两侧调制有明显的0.160阶次的边频带,为内齿圈故障阶次边频带Or。
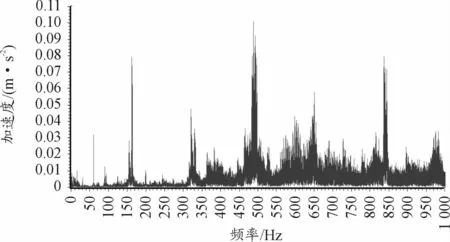
图9 故障振动加速度频谱图
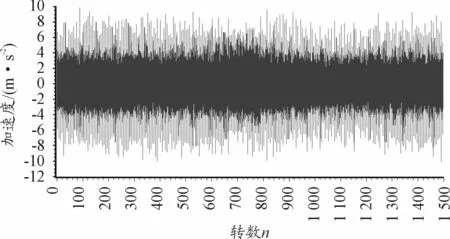
图10 故障振动加速度阶次波形(角度域信号)
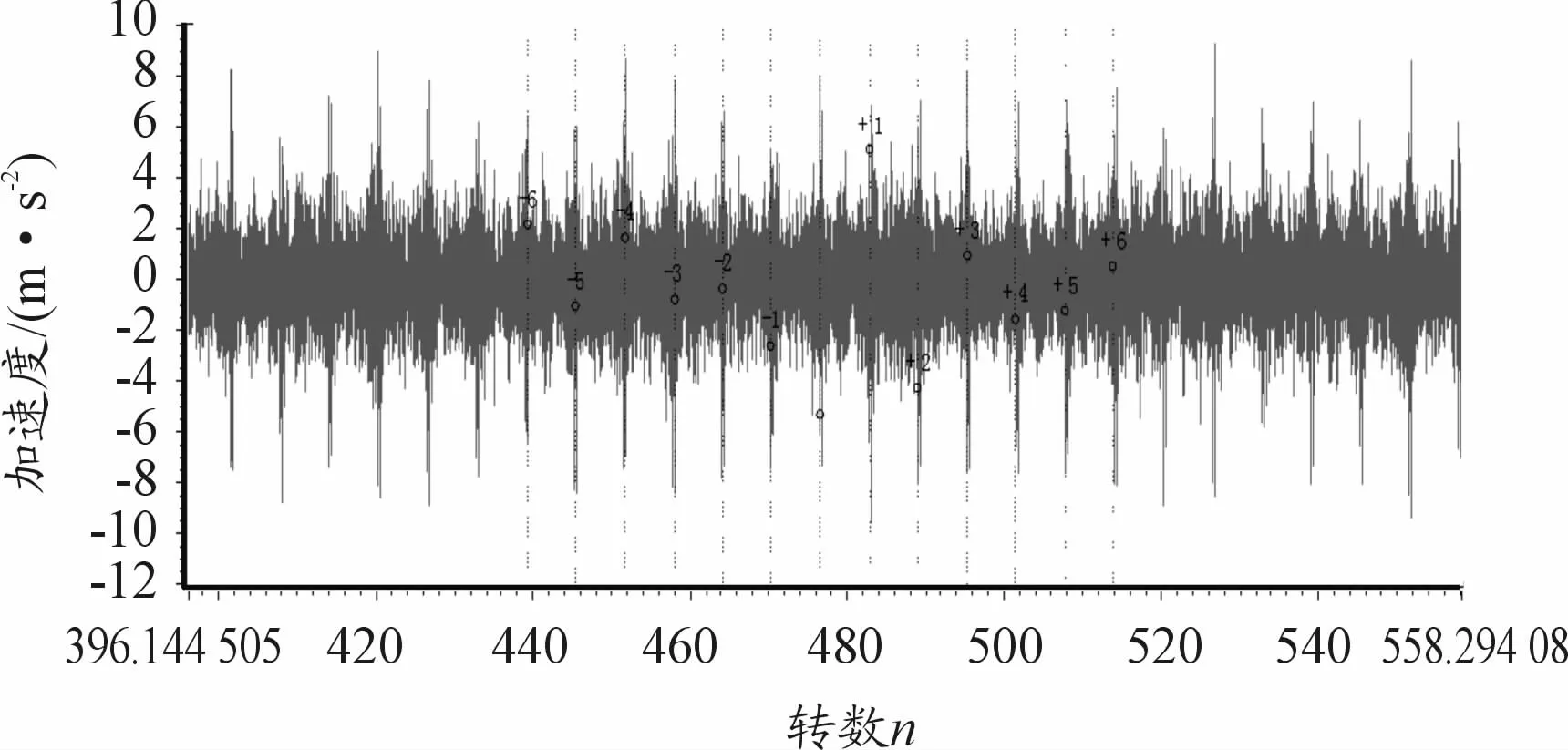
图11 故障振动加速度阶次波形(角度域信号)放大图
从故障阶次谱可以看到在啮合阶次两侧调制有大量的边频带,在齿轮啮合阶次的fmo(5.406)两侧,调制有少量且幅值低的fmo±mor(0.160)阶次边频带,在齿轮啮合阶次的2fmo(10.812)两侧,调制有少量且幅值低的2fmo+mor(0.160)阶次边频带。在齿轮啮合阶次的3、4倍频两侧调制有大量的3fmo±mor(0.160)、4fmo±mor(0.160)阶次边频带,边频带数量多且幅值高,如图12、13,在啮合阶次的两侧并没有发现调制有太阳轮和行星轮的故障阶次。且时域波形等间隔冲击频率、阶次波形等间隔冲击的阶次以及阶次谱调制的边频带阶次都一致。此时可以判定齿轮箱行星轮系的内齿圈可能存在损伤。随即用工业内窥镜对齿轮箱行星轮系的齿面情况进行的内窥镜检查,发现在内齿圈齿面存在剥落等异常情况,如图14所示。
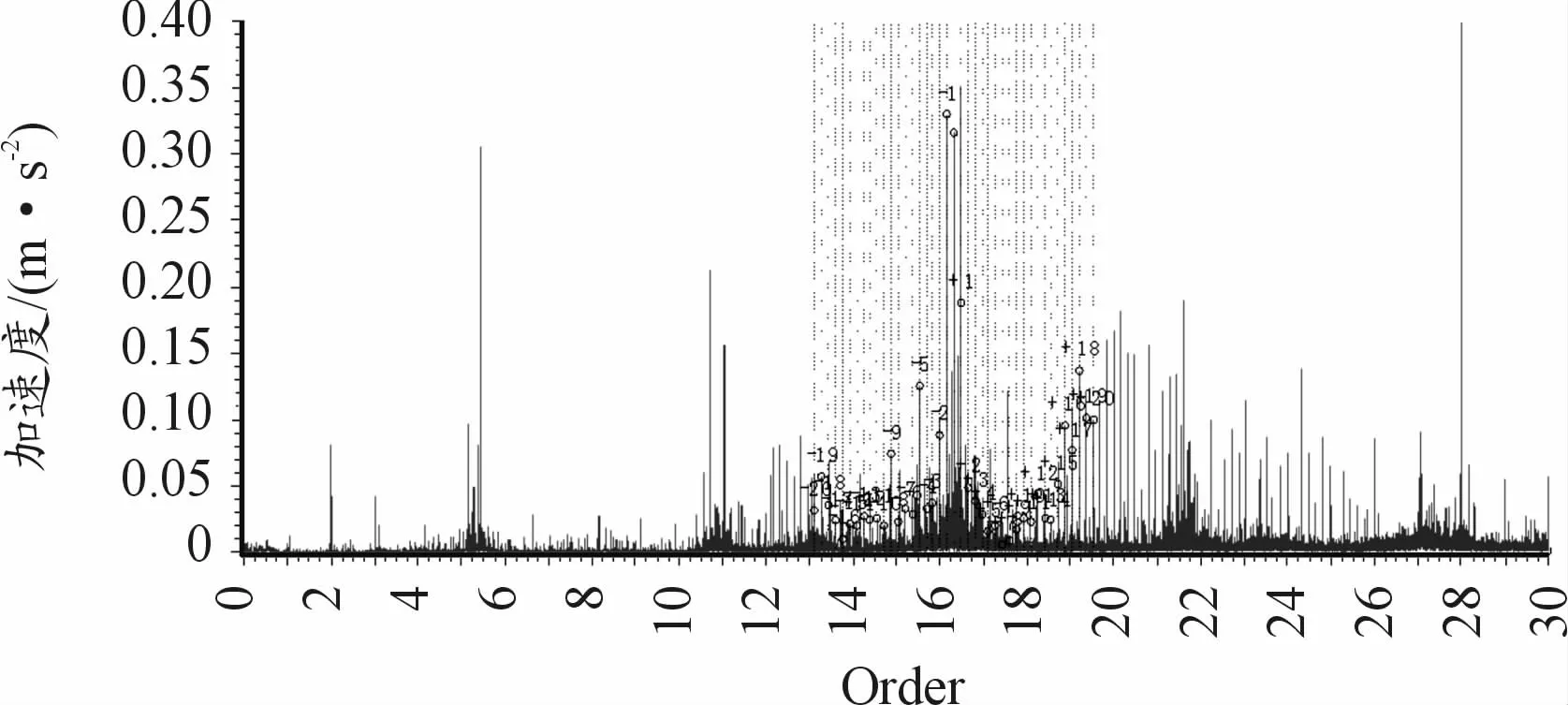
图12 故障振动加速度阶次谱图
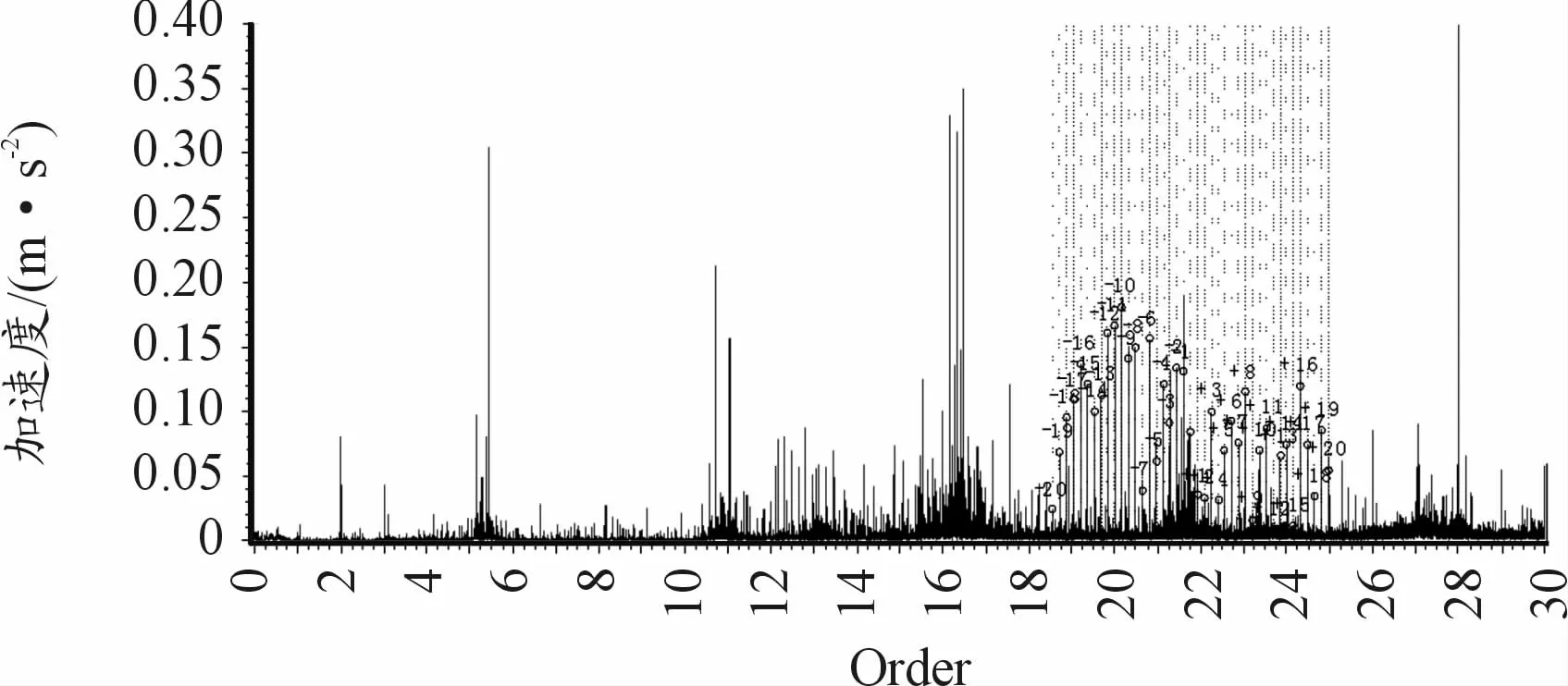
图13 故障振动加速度阶次谱图

图14 内齿圈齿面损伤剥落图
通过对比图9、12,可以清晰地发现,使用了阶次跟踪技术后,阶次跟踪能清晰识别故障阶次,而频谱由于“模糊”现象不能有效识别故障频率,表明阶次跟踪在非平稳信号故障诊断中的重要性,这一点在低速重载的行星轮系上显得尤为重要。
5 结论
本研究采集风电行星齿轮箱时变工况下振动信号,分析了时变工况下行星轮系各个部件的故障阶次特征,运用计算阶次跟踪方法分析了齿轮箱行星轮系的非平稳振动信号,对行星轮系的故障进行了诊断和精确定位,结果表明此方法对时变工况下行星轮系故障诊断十分有效。
