再探高中数学中的小组合作学习模式

吴铖鑫

[摘  要] 随着新教学理念的衍生，小组合作学习作为一种科学有效的教学策略，实现对教学模式的创新，达到真正意义上的增效减负. 文章以“椭圆及其标准方程”的教学为例，展示了运用小组合作学习模式的教学策略，并提出了自己的教学感悟.

[关键词] 小组合作学习;高中数学;增效减负

[⇩] 前言

随着新教学理念的衍生，作为一线教师首先需要考虑的是采用何种教学模式才能让学生容易接受新知识，增强数学能力，提高数学素养，进而使教学效率最大化. 笔者认为，变传统教学模式为小组合作学习模式，让学生生动活泼地合作探索和互动交流，就能更好地发挥学生的创造性与主动性，在积极主动参与中提高教学效率，达到真正意义上的增效减负.

基于这样的认识，笔者在日常实践中开展了合作学习的教学模式多年，一边实践一边摸索，一边积累一边改进，最终有了这样的变化：往日学生觉得异常枯燥的數学课堂活跃起来了，学生积极展示的情怀有了，表达能力更强了，数学思维逐步活化了. 学优生和学困生的差距也越来越小了，教学效果整体提升了.

[⇩] 组建合作学习小组

学习小组需要在教师的班级管理的大前提下，基于班级人数和学生具体情况进行划分、组建. 每组6～8人，本班共有学生42名，笔者根据具体学情将学生分为6个梯队，一共7个小组，第一梯队是班级的1～7名学生.由此类推进行划分，这样每个小组的6名成员便来自6个不同的梯队. 设立第一梯队的学生为组长，第二梯队的学生为副组长辅助组长的工作. 这里要重点说明的是，组长与副组长的选择不仅仅需要考虑学习成绩，更重要的是需要考虑其管理能力、自控能力和组织能力等，当然还需要协调正副组长的默契程度，只有这样整体协调考虑，才能利于合作学习的开展，从而促进所有学生的共同进步.

[⇩] 教学过程设计

有了明确的分组，下一步自然就是展开小组合作学习. 为了更清晰地彰显数学学科特色，笔者根据具体教学实际，在预设、实践、改进的多次循环实践中，初步拟定了一般教学流程. 下面笔者就以“椭圆及其标准方程”一课为例，结合自身的一些做法进行总结.

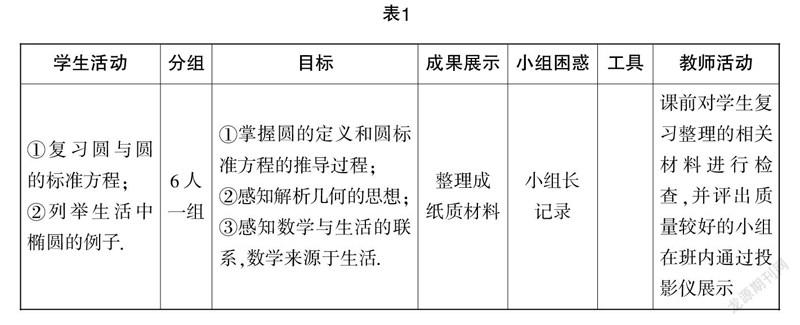
1. 预习环节（如表1）

教学说明：学生是具有创造能力的个体，为他们提供充足的合作学习时空，他们可以发挥出巨大的能量. 在课前，教师设计好问题，并给予合作学习的时空，让学生去感知新知，形成认识. 这样一来，不仅可以使教师对学生的已有认知做到心中有数，更重要的是通过复习巩固，让学生对新课的学习有一定的认识，从而为课堂学习奠定良好的知识基础.

2. 导入环节

问题情境：（1）在一个圆柱形水杯中装上半杯水，再放置于一张水平桌面上，观察其截面是什么形状. （圆形）

（2）端起水杯开始喝水，此时水杯倾斜，再次观察水平面，此时截面又是什么形状？（椭圆形）

（3）由此可见，椭圆与圆有着密切的联系. 根据圆的定义，可知将细线的一端固定于黑板，另一端系上一支粉笔，拉紧细线绕此固定点旋转一周，即可得出“圆”. 那么，现将圆心从一点变为两点，细线的两端固定于这两点上，用粉笔挑起细线后拉紧细线移动粉笔，你觉得画出的图形是什么？（椭圆）

教学说明：这里的问题不仅贴近了日常生活，又不失新颖，易引发学生的数学思考. 这样的课堂导入既轻松又自然，还能充分感受数学与日常生活的联系，从而增强学生的数学素养.

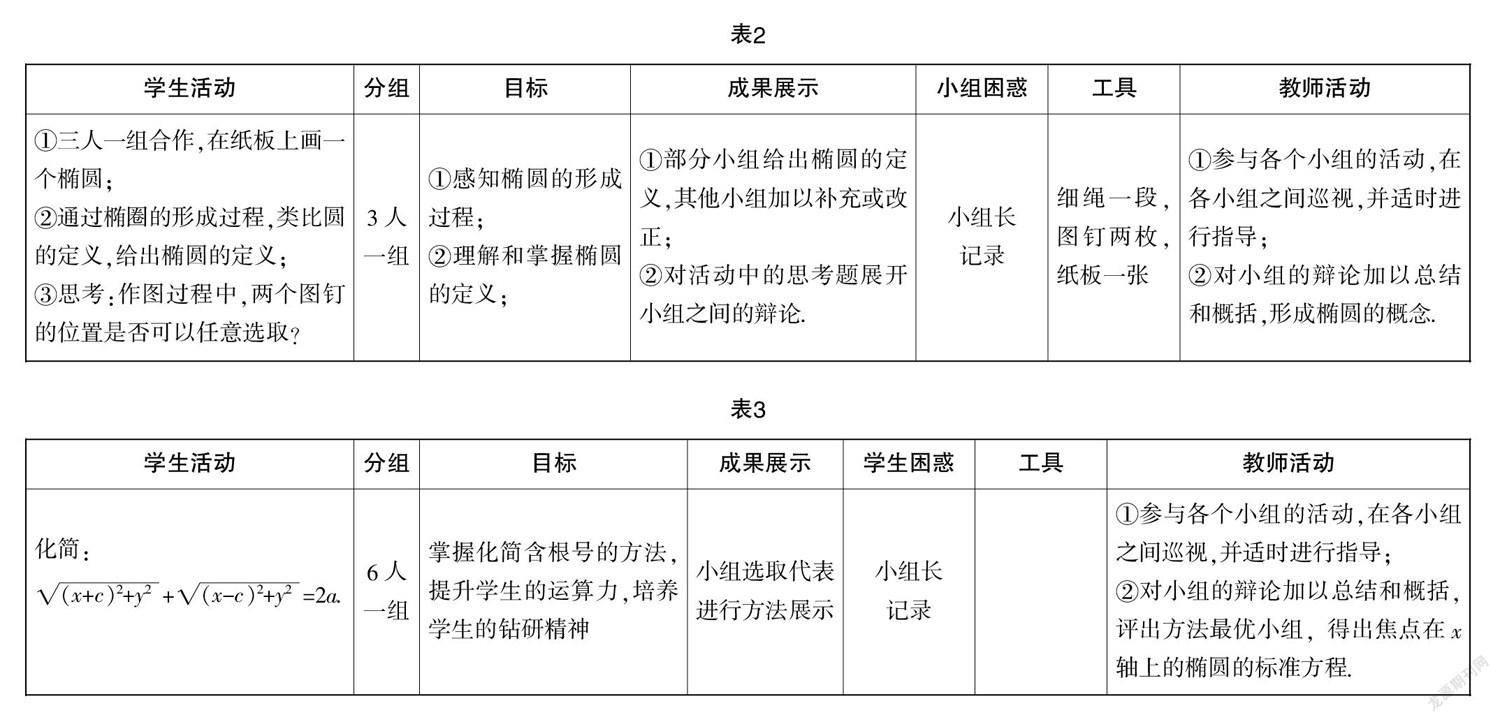
3. 新知探究环节（如表2）

教学说明：这里教师紧紧抓住合作学习的效能，引导学生实验操作、互动讨论、猜想结论，从而在习得新知的同时，学会思考、探究、概括和表达的方法，水到渠成地提升数学能力.

4. 概念建构环节

问题1：椭圆的定义中，对常数有何要求？这个常数是否可以是任意的正实数？（需添上“常数>

F

F”加以限制）

问题2：倘若“常数=

F

F”，轨迹会如何？“常数<

F

F”又会如何？（当“常数=

F

F”时，轨迹是线段FF;当“常数<

F

F”，轨迹不存在）

问题3：请试着总结椭圆的定义. （之后，教师用PPT呈现椭圆完整的定义，并不失时机地推出焦点和焦距的定义）

问题4：请尝试回忆用坐标法求动点轨迹方程的一般步骤.

问题5：根据以上的一般步骤，试着建立焦点在x轴上的椭圆的标准方程.

教学说明：整个过程中，学生亲历椭圆概念的引入和标准方程的建立的探究过程，加深对其本质的理解和认识. 当然，此处涉及本课的重难点“如何化简椭圆方程”，教师通过点拨和诱导很好地引导学生思考“如何去根号”，完成了难点的突破. 很显然，在这个环节中教师放弃了小组合作学习，主要是为了避免流于形式的合作学习，让每个学生都能进行思考和表达，而不仅仅让学优生“独领风骚”.

5.小组合作环节（如表3）

学生经过小组合作学习后，形成了以下三种化简方程：①移项后两次平方法;②等差数列法;③三角换元法.

教学说明：经验可以创造成功，这里教师引领学生进一步熟悉“利用坐标法求动点轨迹方程”，强化化简含根号等式的方法，让学生真正由体验到领悟，进而驱动深度学习.

6. 新知应用环节

例1：到点F（-2，0）与点F（2，0）的距离之和是6的动点M的轨迹是椭圆吗？（是）

例2：到点F（-2，0）与点F（2，0）的距离之和是4的动点M的轨迹是椭圆吗？（不是）

例3：已知F（-1，0）与F（1，0）是椭圆C的两个焦点的坐标，且椭圆上的一点M到两焦点的距离之和是4，试求出椭圆C的标准方程.

7. 归纳提炼环节

略.

8. 课后延伸环节（如表4）

教学说明：本环节主要是再次巩固新课学习中所涉及的有关知识点及数学思想方法，以促进学生水到渠成地建构知识链，让学生在生长知识的同时生长思想，生长思想的同时生长经验，生长经验的同时生长智慧.

[⇩] 小组合作学习下的几点反思

1. 明确目的，不能流于形式

课堂教学是追求“方法”的，小组合作学习也是一样，不少教师认为，建立小组后学生围坐一起讨论就是合作学习了. 然而基于这样的理念，在实践教学的过程中，学生争执不下的情形并不少见，学生探讨不出正确结论的情形更是屡见不鲜. 倘若此时教师依然置身事外，那谈何优质高效？事实上，小组合作学习更需要有明确的目的，不能为了讨论而讨论，为了合作而合作，应在教师的组织、引导和调控下，激起思维的涟漪，点起思维的火花.

2. 给予边缘化学生更多的关注

日常教学中，我们可以发现小组合作学习中，积极思考并踊跃发言的总是固定不变的几个学生，长此以往，学优生和学困生的差距会日益明显，这显然违背了合作学习的本意. 事实上，合作学习的模式下，不管是组长还是教师，都应给予边缘化学生更多的关注和鼓励. 本课中，无论在概念建构环节还是小组合作环节，教师和组长都能及时地关注学困生的反馈意见，给予他们优先发表观点的机会，对他们发表的独特见解给予更多的得分奖励，让他们感受到合作学习的乐趣.

3. 选好时机，让合作更高效

合作学习很多时候并非外在的形式，更多时候是一种内在的需求，只有在学生产生这种需求时，合作学习的效果才能充分显现. 因此在本课中，笔者并没有在每个环节安排合作学习，仅仅是在预习新知、新知探究、课后延伸这几个环节安排了合作学习，让学生基于自身的认识进行合作讨论，从而真正使学生学习的效果最大化，这样的课堂才能产生“课虽尽，意未尽”的韵味.

总之，在课堂教学中，教师只有强化学科知识，深化对合作学习本质的认识，以合理的分组为前提，以多样化的问题为载体，选好合作学习的时机，给予边缘化学生更多的关注，这样才能使合作学习落到实处，才能真正打造优质高效的数学课堂.

3335501908267