源于兴趣 意于探究 成于建构

蔡泽曦

[摘  要] 文章以“全等三角形的拓展”为例，探讨了新课程理念下实施探究式教学的策略：以“教什么”为探究式教学的立足点;以“为何而教”为探究式教学的切入点;以“如何教”为探究式教学的生长点.

[关键词] 探究式教学;建构;兴趣

问题的提出

基于应试教育的大背景，不少教师过于关注学生的考试分数，而忽视了学生的学习体验，致使教学过程“涸泽而渔”. 新课程理念关注学生的兴趣，关注学生的探究，从而对教师的教学提出了更高的要求. 下面以“全等三角形的拓展”的教學实践为例，谈谈如何实施探究式教学.

教学过程

1. 提出问题，激发兴趣

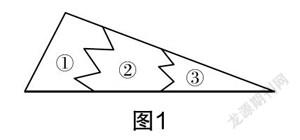
问题：淘气的强强在与弟弟打闹时不小心打破了如图1所示的一块三角形玻璃，妈妈准备去配一块新玻璃，该拿哪一块去玻璃店才能配到和原先一模一样的玻璃呢？为什么？

（问题提出后，学生议论纷纷，很快就有学生举手发言）

生1：我认为应该拿第①块. 因为两个角对应相等，且其夹边对应相等的两个三角形是全等三角形.

设计说明 教师通过简单而有趣的生活问题进行导入，既能让学生在解决问题的过程中复习旧知——全等三角形的判定方法“ASA”，又能让学生明晰“判定两个三角形全等需要三个条件”. 这样的设计既能为全等三角形的拓展做好充分准备，又能有效地激发学生的探究欲望.

2. 精设探究，思维生长

师：下面，我们来拓展“ASA”判定法. 以其他条件来置换“两个角”和“夹边”，请完成如下问题.

______分别对应相等，且______对应相等的两个三角形是全等三角形. （请填上适当条件，使命题完善）

生2：填“两条边”和“两条边的夹角”，就是“SAS” 判定法.

生3：填“两个角”和“其中一个角的对边”，就是“AAS” 判定法.

师：刚才大家所说的都是课本中的定理. 那么，谁能跳出课本定理的框架，想出一个新的命题呢？

师：（拾级而上）现在我们还是保持两个角不动，改变“夹边”这一条件，是否也能全等呢？请完成下面的问题.

两个角对应相等，且______对应相等的两个三角形是全等三角形. （把命题补充完整，变成一个新命题）

生4：两个角对应相等，且第三个角对应相等的两个三角形是全等三角形.

生5：不可以这样填吧，这样的两个三角形不一定全等，但一定相似.

生6：我觉得这里也可以像生4这样填写，问题中只说补充完整命题，并没有限制其必须是真命题.

师：生6提出了一个非常正确且创意的思考，从题意出发，我们可以发现这里并没有限制命题的正确性，这样就给予了我们思考的多样性.

生7：那可以填写的内容就多了，可以填“角平分线”“中线”“高”等.

设计说明 教师控制一个变量后设计了一道具有开放性和探究性的变式问题，让学生尝试通过变换条件来思考，从而触发了学生的创造性思维. 学生经过多样性思考，得出了多个可塑性答案，生成了新的命题，这样的探究极大地拓宽了学生的思维宽度.

师：那现在再变化一下题目，题目如下.

两边对应相等，且______对应相等的两个三角形是全等三角形.（把命题补充完整，变成一个新命题）

生8：可以填“第三边”，即“SSS”判定法.

生9：可以填“夹角”，即“SAS”判定法.

生10：可以填“两边的夹角的外角”.

生11：可以填“任意两角”或“任意一角”.

生12：可以填“第三边上的高”.

师：类比生7的答案，还有什么思路吗？

生13：可以填“一组角平分线”“一组中线”或“一组高”.

设计说明 类比前一个问题，教师继续引领学生进行数学探究，使学生在类比思考中发现问题. 整个探究活动是在学生独立、自主的基础之上进行的，有利于学生自主探究能力的提高、类比思维的发展，且活动过程组织有序，学生主动探究，教学效果显著.

3. 充分联想，实现建构

师：经过刚才一系列探究，我们得出了许多新问题，下面老师选取几例继续探究. 以下三种情形中的两个三角形是否全等？

情形1——两角对应相等，一组角平分线对应相等;

情形2——两角对应相等，一组高对应相等;

情形3——两角对应相等，一组中线对应相等.

生14：判断起来难度颇大，因为它们都不具备判定三角形全等的条件，不过，我感觉它们都是真命题.

师：事实上我们可以做如下思考. 两个角对应相等的两个三角形相似，倘若相似比并非1 ∶ 1，则对应中线不可能相等，但此处与题设矛盾，所以相似比只能是1 ∶ 1. 也就是说，这两个三角形全等.

师：进一步地，我们再来思考下面两个问题.

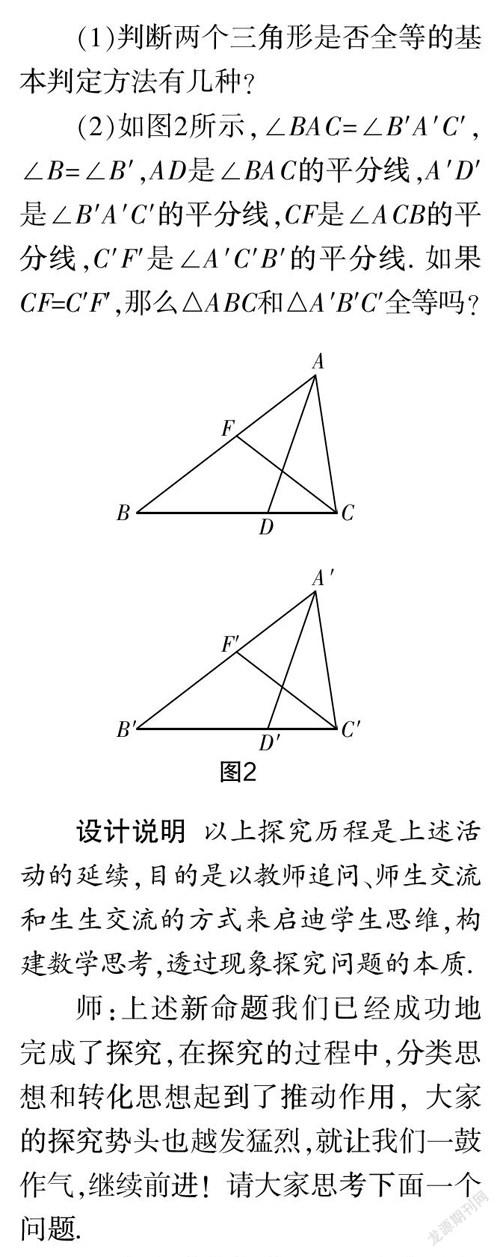
（1）判断两个三角形是否全等的基本判定方法有几种？

（2）如图2所示，∠BAC=∠B′A′C′，∠B=∠B′，AD是∠BAC的平分线，A′D′是∠B′A′C′的平分线，CF是∠ACB的平分线，C′F′是∠A′C′B′的平分线. 如果CF=C′F′，那么△ABC和△A′B′C′全等吗？

设计说明 以上探究历程是上述活动的延续，目的是以教师追问、师生交流和生生交流的方式来启迪学生思维，构建数学思考，透过现象探究问题的本质.

师：上述新命题我们已经成功地完成了探究，在探究的过程中，分类思想和转化思想起到了推动作用，大家的探究势头也越发猛烈，就让我们一鼓作气，继续前进！请大家思考下面一个问题.

“两条边对应相等，且一组角平分线对应相等的两个三角形全等”，这个命题需要分类吗？为什么？

生15：需要，因为第三条边是否对应相等有待考量.

师：不错，这就是这一类问题与刚才所探究问题的不同之处. 显然，我们已经没有办法将其中一种情况迅速转化了，所以分类不可避免. 那如何操作呢？下面分小组合作讨论，之后汇报交流.

……

设计说明 在教师的启迪、点拨和引导下，学生立足于审视教材的高度进行探索和质疑，深刻感受到了探究之趣、收获之悦，更重要的是能生长数学思维，感悟数学思想，培养探究能力.

教学反思

1. 探究式教学的立足点：教什么

探究式教学的立足点是课题的选择. 从对本节课教学内容的理解中我们可以看出，教师在选择本课题时不仅考虑到了教学生学习知识，更多地考虑到了教学生如何思考，教会学生如何思考. 因此，教师在讲解完“全等三角形”的相关知识后，应适度开发和利用教学资源，不失时机地融入这样一个拓展课题，让学生从判定两个三角形全等的方法入手，探究置于新环境下的两个三角形是否为全等三角形，从中感悟分类讨论思想和转化思想，发展学生的自主探究能力，培育学生发现问题和提出問题的能力.

2. 探究式教学的切入点：为何而教

探究式教学的切入点是为什么教. 因此，厘清教学内容的来龙去脉和本质相当重要. 从内容设计上来看，学习了全等三角形的判定，必然要跟进其应用，这样才能为后续的教学奠基. 而事实上，学生对于判定法的应用大多是生搬硬套，没有从根本上理解，基于此，教师设计了这样一节拓展课，以趣味性导入激发学生的兴趣，引发学生思考，让学生通过自主思考创造性地提出问题，并在这个过程中学会类比思考，从而学会用分类讨论思想和转化思想解决问题.

3. 探究式教学的生长点：如何教

一个独特的问题情境可以引发学生的好奇心，学生在好奇中探究，在探究中发现，在发现中质疑，在质疑中分析，从而形成解决问题的策略. 因此，对于本课，教师通过一个创意性的生活问题引发学生进行探究活动，使学生在探究中拓宽认知，直至完成对全等三角形判定方法系统的理解与认识，让知识的建构水到渠成、浑然天成.

结束语

总之，对于探究式教学，教师应有目的地设计创意问题，通过循序渐进的过程，让整个班级共同进步. 这个过程应充满挑战和乐趣，应充分展示学生的思维与进步，应有利于培养学生的积极探究能力，这样才能使每个学生都成为积极向上的探究者、发现者和建构者.

3226501908291