新课改背景下数学概念教学的策略

陆茗竹

[摘  要] 新课改背景下的概念教学，更重要的是探究概念的形成过程，引导学生从真正意义上掌握概念的内涵与实际应用. 文章认为当下数学概念教学的方法有：因材施教，注重导入;紧扣本质，加强探索;及时巩固，深化理解;联系生活，实现迁移.

[关键词] 概念;教学策略;探究

概念是指人脑对客观事物本质属性的反映. 随着新课改的推进，对概念教学的要求已由原来的“理解、掌握与运用”转化为如今的“探究与运用”[1]. 个别用词的变化，却引发了一场以概念教学为核心的教育改革浪潮. 实践中，想让学生自主探究抽象的概念，教师可以教学方法为突破口，用知识的正迁移凸显概念的内涵，激发学生的探索欲，强化学生对概念的理解与掌握.

因材施教，注重导入

俗语说：“良好的开端是成功的一半. ”课堂导入是教学的第一步，导入的成败基本决定了本节课的成败. 丰富、有趣的导入能有效地激活学生的探索欲，因此，概念教学时，教师应综合考虑学生的特点与教学内容，因地制宜地设计概念导入的方法.

每个概念都有自己的特点，而每个学生又有着不同的认知水平与社会经验. 因此，在概念导入时，教师可从诸多因素出发采用不同的方法引入概念，如在学生已有的认知水平与生活经验上引入;在例题教学过程中引入;以一般到特殊的方式引入等. 多样化的引入方法，能有效地激发学生对概念的探索欲.

案例1  “图形的旋转”的概念教学.

师：新课之前我们先回顾一下平移的概念，哪位同学说说平移的核心是什么？

生1：平移的图形大小和形状不会发生变化，只是位置发生了改变.

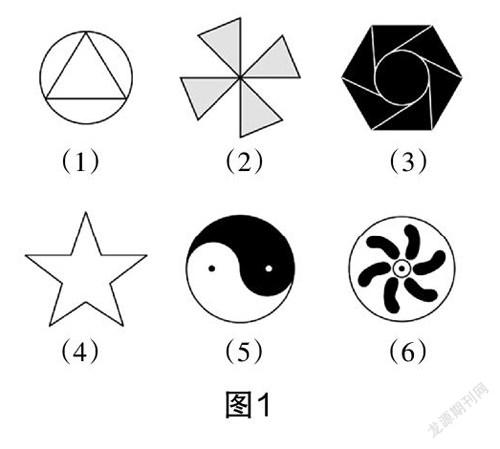
师：很好，现在大家观察图1，假设这几幅图在不断旋转，你们来说说它们之间有没有什么异同点？

生2：这些图在转动的过程中，大小与位置是不会发生改变的.

师：很好！生活中有哪些类似的物品？

生3：我觉得生活中的钟表、摩天轮等跟这几幅图有异曲同工之妙.

师：的确. 如果我们将此类图形的运动称之为旋转，谁能说说旋转的具体概念？

生4：图形围绕一个定点转动称为旋转.

师：有补充吗？

生5：应该在同一平面内.

师：非常好！这个条件不能丢. 现在请一位同学完整地总结下旋转的概念.

……

对于图形的旋转，若没有具体事物作为参照，纯粹凭借教材中提供的文字与教师的讲解去理解，会因内容过于抽象而导致学生难以理解其内涵. 为了打破这一僵局，教师在概念导入环节引入一些图形，并运用学生在生活中所熟悉的摩天轮、钟表等实际物品帮助其理解，自然又合理. 学生在生动、形象的导入环节，不仅理解了旋转的概念，更重要的是掌握了数形结合的数学思想.

紧扣本质，加强探索

在新课改背景下的现代化数学课堂教学，对概念的要求不再是簡单的识记，更重要的是要弄清楚每个概念形成的始末[2]. 因此，教师应精心做好教学设计，利用课堂这片天地让学生厘清每个概念的来龙去脉，引导学生从概念产生的背景、形成过程与适用范围等角度理解概念的性质与内涵.

案例2  “负数”的概念教学.

师：观察图2，图上显示了珠穆朗玛峰与吐鲁番盆地的海拔，图示标出的“8848 m”与“-155 m”代表了什么意思呢？

生1：代表了珠穆朗玛峰在海平面上8848米，而-155 m则说明吐鲁番盆地比海平面低155米.

师：非常好！既然是以海平面为参照计量出来的数据，那么海平面应该用什么来表示呢？

生2：我觉得海平面应该用0来表示.

师：哦？为什么？

生2：具体的我也不清楚，我是参照温度计来说的. 温度计有零上多少摄氏度与零下多少摄氏度之分，区分点为0 ℃.

师：太棒了！这是典型的将生活知识迁移到学习中的表现. 那么这个0跟我们以前学的0一样吗？它代表“没有”的意思吗？

生3：感觉不太一样，这个0不能称为没有，或许可以理解为一个分界线.

师：有点意思！你们能列举一些类似的生活实例吗？

生4：例如生活中蓄水池所标记的标准水位记为0，以上为正数，以下为负数.

……

学生对一张地图进行观察、分析与概括的过程即概念的抽象过程. 学生在此过程中感受、感知、感悟负数概念的形成与发展，从本质上真正地理解概念的内涵. 这种由具体到抽象的概念教学方式既符合学生身心发展的需求，又为数学核心素养的培养奠定了一定的基础.

及时巩固，深化理解

学生在对概念有一定认识后，从表面上看已经掌握，当遇到具体问题时，却有不少学生无法准确地分析与判断. 为了突破这种障碍，在学生初步认识概念之后，教师可通过变式训练或举反例等方式来帮助学生更深入地剖析概念，让学生从本质上深化对概念的理解，做到及时巩固，以达到掌握概念并能灵活运用概念的目标.

案例3  “函数”的概念教学.

在学生对函数的概念有一定了解的基础上，教师可设计以下教学步骤，以帮助学生更好地理解函数的概念.

步骤一：观察下列式子，判断哪些是二次函数？

①y=2

x-2-;

②y=x（x-3）;

③y=（x-1）（x+1）;

④y=（x-2）2-x2.

学生在判断哪些式子为二次函数的时候，会调动记忆中函数的概念，逐个分析式子的过程就是强化记忆的过程. 通过对式子的辨析，能有效地加深学生对函数概念的理解，从而达到巩固与强化概念的作用.

步骤二：将一根2米的铅丝折成一个0.1米宽的长方形，此长方形的长为多少米？若折出的宽为0.2米，长又是多少米？分析：长是宽的函数吗？理由是什么？

这是一道实际运用题，将函数的概念代入到实际情境中进行分析，分析这根铅丝所折成长方形的宽和长之间的关系，理解函数的实际应用价值. 解决这个问题的过程就是灵活运用概念的过程，学生在知识的形成与发展中深化了对函数概念的认识.

步骤三：列表，观察表格中的数据，尝试将一个变量理解为另一个变量的函数，说说理由.

学生自主列表的过程就是对概念运用的探索过程，表格中两组变量的变化呈现出一定的规律性，这也是函数的两个变量之间的关系. 学生在对表格的分析中不仅巩固了函数的相关概念，更重要的是获得了自主探究能力，这为后期的学习奠定了坚实的基础.

联系生活，实现迁移

生活是概念产生的源头，概念学习最终又为生活服务[3]. 充分认识生活与概念的关系，切身体会概念对生活的影响，能让学生发自内心地喜爱数学这门学科，并为学好这门学科夯实基础. 学以致用是学习的目标，在概念学习后，运用一些贴合生活实际的问题激发学生的应用意识，能有效地深化学生对概念的理解.

案例4  “函数”的生活实例.

①甲城与乙城之间的距离为200千米，某车从甲城开往乙城所需的时间y（h）与均速x（km/h）之间的函数关系式为y=.

②计划修建200千米长的公路，所需的时间y（h）与平均日完成量x（km）的函数关系一样为y=.

师：根据以上两个生活实例，你们还能找到类似运用函数的生活实例吗？

（学生就此问题进行合作学习）

生活中有很多实例与函数有着密切的联系，教师以两则常见的生活实例为引子，鼓励学生用合作学习的方式自主探索类似的生活实例. 这种方式不仅体现出知识与生活的密切相关性，更重要的是培养了学生的实用意识，将概念与生活相联系，能有效地提高学生的生活技能与认知水平.

总之，概念教学作为数学教学的重要环节之一，是学习的核心，是公式、法则与定理等的基石，学好并灵活运用概念能为后续的学习奠定坚实的基础. 作为教师，不论是在概念的引入环节，还是在概念的探索或巩固环节，均需引导学生从根本上理解、掌握并运用概念，深化学生对概念理解的同时，让概念更好地为生活服务.

参考文献：

[1]中華人民共和国教育部. 义务教育数学课程标准（2011年版）[S]. 北京：北京师范大学出版社，2012.

[2]施晓丹. 本固方可枝茂——关于强化初中数学概念教学的探索[J].初中数学教与学，2014（3）.

[3]濮安山.初中生函数概念发展研究[D]. 长春：东北师范大学，2011.

3624501908299