加强知识联系,提升解题能力
2021-03-21温莹
温莹


[摘 要] 随着新课改的不断深入,以“题海战术”提升解题能力的时代已然成为过去. 文章认为建立知识联系的方法有单元系统化、专题系统化与学科系统化. 同时,文章以一道综合题的教学为例,具体谈谈建立知识联系、提升解题能力的操作方法.
[关键词] 解题能力;知识联系;解题教学
新课标提出:“学生能力的培养应以解题为突破口,让学生在解题实践中提升各项能力与数学核心素养. ”可见,培养学生的解题能力是数学教学的核心内容之一. 而解题能力又属于一种个体独特的心理形成物,具有一定的特殊性. 实践证明,从知识之间的联系着手,引导学生逐层深入地建构完整的知识体系,可帮助学生形成可持续发展的解题能力.
建立知识联系的方法
不少学生都有这样的困扰:到初中后数学内容纷繁复杂,方程、函数、几何等千变万化的知识点让不少学生感到数学学习就是一团乱麻,说不清、道不明,剪不断、理还乱. 其实,数学是一门系统性的学科,只要定期整理、练习、巩固,就可以建构成新的知识体系,体系一旦建成,解题能力就会得以发展.
(1)单元系统化:针对一些相对独立的知识点,教师可鼓励学生以单元为单位,进行一定的归纳与总结,形成一个“知识链”. 学生在“知识链”的提炼中,逐渐在大脑里编织成一张新的以单元为单位的知识网,而每个知识点则是这张知识网的结点.
(2)专题系统化:专题系统化主要是指打破教材所设定好的单元或章节体系,将同类的知识点或解题思想归纳在一起进行提炼、总结,以形成新的知识体系,让学生能更好地解决同类问题. 例如,化归思想是解题中常用的数学思想方法之一,常涉及配方法、待定系数法、代入法、由抽象到具体的方法等. 我们可以将这些方法运用到涉及化归思想的问题,归纳在一起进行专题复习,以提高学生的解题能力.
(3)学科系统化:学科系统化是指站到一定的高度,从总体上审视学科结构. 将数学看成一个整体的系统(如一棵树),而这个系统又由几个子系统(树干)组合而成,子系统又由更小的子系统(树枝)构成,这些更小的子系统由一个个的知识点(树叶)所组成.
解题教学建立在学科系统化的基础上,会让学生充分领略数学学科独有的魅力,了解其基本原理,从而在大脑中建构成完备的数学知识体系,为形成举一反三的解题能力奠定基础.
教学案例
原题 如图1所示,四边形ABCD为☉O的内接正方形,已知AB=4且PC与PD分别为☉O的两条切线,切点分别为C,D. (1)求☉O的半径;(2)若已知点E为BC边的中点,连接PE,则PE的长度是多少?(3)如图2所示,点M为BC边上的任意点(点B,C除外),若以M作为直角的顶点,作∠AMN=90°,与直线CP相交于点N,求证:AM=NM.
1. 学情分析
本题主要考查学生对正方形和圆的综合认识. 其中,问题(1)比较简单,只要有一定的基础,就能顺利结题;问题(2)的难度适中,符合大部分学生的认知水平;问题(3)对于大部分学生来说,有一定的困难. 笔者发现不少学生直接放弃了问题(3)的解答,也有小部分学生虽作了一些尝试,但最后仍以失败告终.
基于学生原有的认知,要求證AM=NM,通常以添加辅助线、构造全等三角形为思维的切入点. 但全等三角形、圆和正方形在教材或教学中属于不同板块的内容,它们不在同一时期学习,与学生最近发展区的距离有点远. 这就需要教师将不同专题的内容融合在一起,建构新的知识体系. 本题最大的挑战在于如何添加辅助线.
为此,笔者充分发挥了本题的教学价值,具体谈谈如何在解题教学中建立知识之间的联系,以突破学生的思维障碍,获得解题技巧,提高解题能力.
2. 常规的解题方法
问题(1):只要结合正方形的判定定理与切线的性质,即可获得☉O的半径.
问题(2):一般利用垂径定理得OE⊥BC,∠ECO=45°,再运用勾股定理即可求得PE的长度.
问题(3):在AB边上取点F,使得BF=BM,利用问题(1)的答案求出∠MCP=135°,由全等三角形的性质与判定定理即可得到AM=NM. 解决此问时,一般通过截长的方法构建全等三角形,但也有学生尝试运用补短法,想利用∠AMN为直角构造出“K字形全等”的方法来求证,但在证明过程中遇到了新的障碍.
3. 建立知识之间的联系,探寻解题技巧
常规解题中,大部分学生都是通过截长法或补短法的运用,将线段AM与NM放到三角形中证得其全等而解决问题. 这种解题思路的侧重点在于全等三角形与正方形,而本题的题设条件既然给出了圆这个图形,是否能充分利用这个条件呢?
若将线段AM与NM构造到同一个三角形(△AMN)中再求证,只要证明该三角形为一个等腰直角三角形即可. 本题中的点A,M,C,N共圆是一个隐含条件,只要发现这个条件,解题将变得轻松. 为了让学生充分感知知识之间的联系,使得数学思维呈递进式发展,笔者设计了以下教学过程:
(1)知识链接.
①如图3所示,点P为线段AB上的一点,且AP=BP=CP=DP,若∠CPB=60°,则∠BDC的度数是多少?
②如图3所示,△ABC与△ABD中,∠ACB=∠ADB=90°,P为线段AB的中点,若∠CPB=60°,则∠BDC的度数是多少?
③如图4所示,△ABC与△ABD中,∠ACB=∠ADB=90°,P为线段AB的中点,若∠DPC=60°,则∠DBC的度数是多少?
设计意图 通过知识链接①,调动学生回忆关于用圆的定义来证明四点共圆的具体方法,契合学生的最近发展区. 知识链接②和知识链接③既是知识链接①的变式拓展,又为学生提供了四点共圆的常见图形,在学生的思维中种下相应的数形结合思想. 该知识链接的过程为学生形成良好的解题方法做好了铺垫.
(2)发散思维.
如图5所示,学生在以上知识链接③的思考过程中,感悟到点A,M,C,N都在以NA为直径的圆O′上.
此时,学生的思维逐渐变得活跃,出现了以下教学对话:
生1:由=可得∠NAC=∠NMC=∠MAB,因此∠NAM=∠CAB=45°.
生2:其实不需要这么麻烦,根据知识链接①可知∠MCN=135°,同时四边形AMCN又是圆O′的内接四边形,因此∠NAM=180°-135°=45°.
生3:我还有更加简单的方法,根据同弧所对的圆周角相等的原理,可直接获得∠MNA=∠MCA=45°.
设计意图 学生的思维在知识链接的引导下得以有效扩散,解题思路与方法一个比一个简洁、高效,此时课堂氛围达到了本节课的高潮,每个学生都对本题产生了浓厚的兴趣. 在此基础上,笔者趁热打铁,提出了新的拓展应用,鼓励学生进行思考,以完善学生的知识结构,为帮助学生建构完备的知识体系夯实基础.
(3)拓展应用.
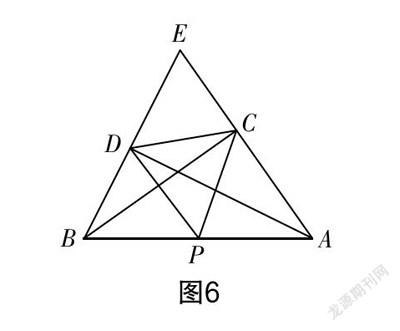
如图6所示,BC,AD分别是△ABE两边上的高,已知AB=2,∠E=60°,且点P为AB边的中点,求△DCP的面积.
设计意图 本题作为“拓展应用”题,旨在帮助学生巩固本节课所学的知识,让学生在知识的链接、思考与拓展中掌握解题技巧,深化对旧知的认识,同时建构新的解题思路与方法,为今后解决类似的综合题夯实基础.
教学思考
1. 由浅入深,引发顿悟
解题教学的关键不在于教会学生解一道题,而在于帮助学生建构解题方法与思想,让学生从一道题中获得新的感知与感悟. 因此,教师在解题教学时,不能就题论题,而应由浅入深地帮助学生回顾旧知,契合学生的最近发展区进行教学才能激起学生共鸣,从而自主发现解决问题的方法.
有些跨度大、范围广的综合题往往令一些学生措施不及,出现思维卡壳也是情理之中的现象. 在本题的解答教学中,笔者则是以三个知识链接点进行预热,帮助学生一起回顾怎样用圆的定义或性质证明四点共圆,并通过基本图形引发学生思考,学生的思维被激活后,就会产生新的感悟. 这为学生后期遇到复杂图形时发现四点共圆做好铺垫.
2. 立足变通,促进发展
学生的发展是教育的主要目的. 充分挖掘题目的教学功能,不仅能体现题目的教学价值,更重要的是能让学生变通思维,让学生认识到解题通法虽有效,但遇到具体问题时应具体、特殊对待,若一味地执着于通法通解的“死胡同”,则会僵化思维,无法形成触类旁通的解题能力.
总之,加強知识之间的联系,对提高学生的解题能力具有重要作用. 但任何能力的提升,均需经历一个漫长而遥远的过程. 因此,作为教师应根据学生的实际情况与教学内容,有针对性地进行长期训练与培养,鼓励学生自主感知、感悟解题技巧,提升解题能力.
3174501908286
