基于APOS理论的因式分解概念教学设计
2021-03-21汪元兴
汪元兴


[摘 要] 概念教学要让学生经历概念的概括过程. 文章以基于APOS理论的因式分解概念教学设计为例,阐述了数学概念教学中要重视学生学习的过程,以及如何帮助学生理解概念.
[关键词] APOS理论;学习过程;概念教学;教学设计
章建跃博士认为,概念是数学思维的细胞,理解概念是数学学习的首要任务,概念教学要让学生经历概念的概括过程[1]. 《义务教育数学课程标准(2011年版)》指出,学生掌握学习知识,应以理解为基础;学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程;学习评价既要关注学生学习的结果,也要重视学习的过程[2]. 因此,在数学概念教学中,必须重视学习的过程,这是帮助学生理解概念的基础.
美国教育学家杜宾斯基等人创立的APOS理论认为,任何一个数学教育理论都应该致力于解决“学生是如何学习的”及“什么样的教学计划可以帮助这种学习的理解”这两个问题. APOS理论还认为,学习者不可能直接学习到数学概念,而是要透过心智结构使所学的概念产生意义才能学习到数学概念. 数学概念的形成要经过“活动(Action)”“过程(Process)”“对象(Object)”和“图式(Schema)”四个阶段[3],其中“活动阶段”可与其他阶段相互交叉,“活动阶段”与“过程阶段”不一定有明显的界线. 文章以基于APOS理论的因式分解概念教学设计为例,阐述了数学概念教学中要重视学生学习的过程,以及如何帮助学生理解概念.
复习回顾,引入新知——活动阶段(Action)
1. 复习回顾
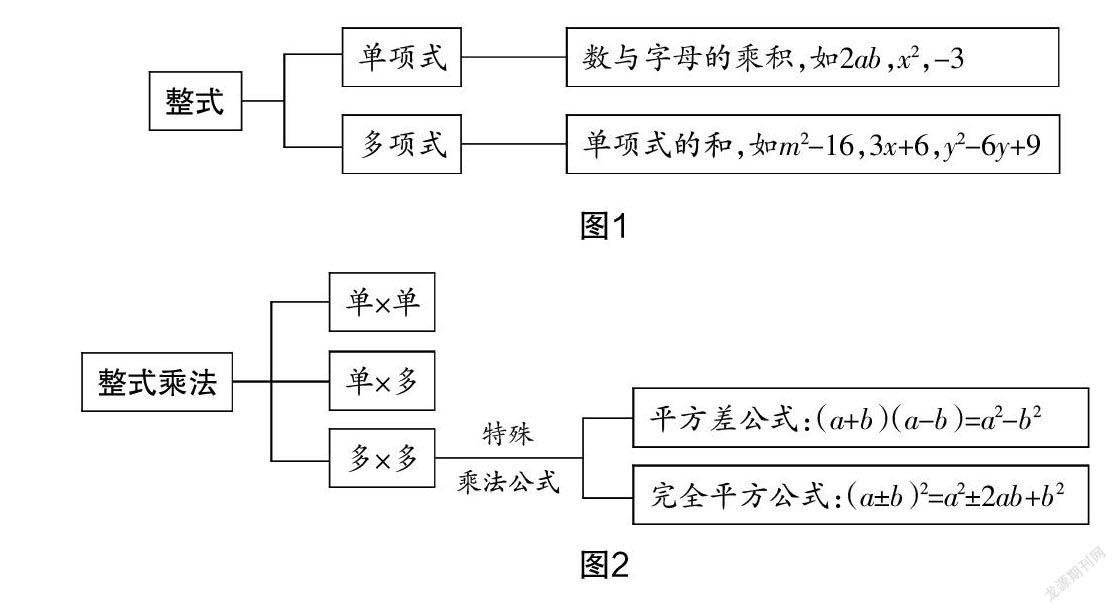
师:在七年级的学习中,我们知道整式包括单项式和多项式,你还记得单项式和多项式的定义吗?(结果如图1所示)整式乘法主要的几种形式如图2所示.
师生活动:教师提出问题,学生口答,教师用PPT展示整式关系图和整式乘法关系图.
设计说明 APOS理论的“活动阶段”的“活动”泛指所有的数学活动,如猜想、回忆、计算、推理等,这里主要是回忆. 通过复习旧知,举例说明多项式的结构特征,突出平方差公式和完全平方公式,为后面讲解因式分解的概念做铺垫.
2. 问题引入
利用整式的乘法运算,可将几个整式的乘积化为一个多项式的形式;反过来,有时需要把一个多项式化为几个整式的乘积的形式.
问题1:993-99能被99整除吗?能被100整除吗?你是怎么做的?
追问:代数式993-99的两项都含有相同的因数99,显然能被99整除;受此启发,能否把993-99化成含有因数100的形式,即993-99=a×100(a为整式)?
学生独立思考后,教师投屏展示两种常见的解法(如图3、图4所示):
小结:这里解决问题的关键是把一个代数式化成几个整式的积的形式.
师生活动:教师提出问题,让学生独立思考后交流展示. 教师用手机投屏展示学生两种常见的解法,组织全班学生评议,总结解决问题的关键是什么,鼓励学生分享思考过程,说明992-1=9800的计算方法,为后面进一步分解a2-1做铺垫,同时渗透最优方案思想.
设计说明 APOS理论认为,概念的引入阶段,要以学生已有的认知结构和认知规律为基础,在认真分析所授概念的具体内容的前提下设置合适的“活动”,让学生亲身经历,主动建构,从而直观理解所学的概念. 這与史宁中教授所强调的教育教学要关注新概念引入的必要性是一致的. 这里的“活动阶段”,通过引导学生回顾整式的相关知识,创设代数式整除问题,让学生经历代数式的计算过程,直观感知因式分解的作用,在心理上认识到学习因式分解这一概念的必要性.
自主探究,感知对象——过程阶段(Process)
问题2:你能尝试把a3-a化成几个整式的乘积的形式吗?与同伴交流.
追问:a2-1可以进一步分解吗?如何分解?
师生活动:教师提出问题,先让学生独立思考,再组织学生交流展示. 类比993-99因数分解的过程,指出字母可以表示数,根据数式通性,可以把99看作a,进而得到a3-a=a(a2-1);对a2-1进一步分解,引导和鼓励学生展示和分享思考过程.
设计说明 通过学生自主探究、合作交流,类比993-99的分解过程,对多项式a3-a进行分解,分享自己的解题思路. 教师在“过程阶段”可以充分地关注学生的学习过程,引导学生初步掌握把一个多项式化成几个整式的积的形式的方法,为后面归纳因式分解的概念提供具体且有一般性的例子,同时引导学生体会数式通性,感受平方差公式的逆运用.
问题3:观察下面的拼图过程(如图5、图6所示),写出相应的关系式.
追问:你是怎么得到相应的关系式的?你能用不同的方法验证关系式的正确性吗?
师生活动:教师抛出问题,先让学生独立思考,再组织学生交流展示. 学生分享解决问题的思考过程,师生共同回顾用几何图形推导整式乘法公式的学习过程,也可以让学生自己动手完成拼图活动,引导学生既可以从拼图前后的面积不变得到相应的关系式(“形”的角度),也可以逆用乘法公式验证关系式的正确性(“数”的角度).
设计说明 APOS理论的“过程阶段”是通过数学活动进一步思考的过程,即当学生经过多次重复的数学活动并对其熟悉后,便会在头脑中自主描述这些数学活动. 本环节设计的两个问题,让学生分别从“数”与“形”的角度认识到一个多项式可以化成几个整式的积的形式. 这是学习因式分解概念的“过程阶段”,一定程度上也可以看作是前面“活动阶段”的延续. 一方面有利于学生加深对几何直观与数学抽象的认识,在心理上抽象出因式分解的本质特征,进入因式分解概念的定义阶段;另一方面有利于学生培养数形结合思想、掌握等面积法,甚至为后续学习因式分解法(提公因式法和公式法)打下基础,有利于因式分解与提公因式法、公式法等建立联系.
合作交流,归纳概念——对象阶段(Object)
问题4:观察下列这几个关系式,它们有什么共同的结构特点?
(1)a3-a=a(a+1)(a-1);
(2)ma+mb+mc=m(a+b+c);
(3)x2+2x+1=(x+1)2.
追问:你能用自己的语言把你发现的说出来吗?(合作交流后,用PPT或黑板展示出来)
定义:把一个多项式化成几个整式的积的形式,这种变形叫作因式分解.
小结:理解概念要抓住关键词.
师生活动:教师提出问题,学生独立思考后全班学生交流展示. 师生评议归纳后,教师给出准确的文字语言描述,为因式分解下定义;随后向学生强调,理解概念要抓住关键词,可结合关系式的结构特点和字面含义加深对概念的理解.
设计说明 概念学习主要依靠的是归纳思维. 学生通过对数学活动所得关系式的分析、比较、综合,归纳出相同或不同关系式的共同特点,经历了从特殊到一般的学习过程,将发现、交流、归纳的结论准确地用文字语言表述出来,为因式分解下定义,这符合APOS理论的“对象阶段”. 同时通过对“理解概念要抓住关键词”的强调、对学生学习概念的学法指导,有助于学生从整体上理解概念的形成过程.
比较分析,巩固概念——图式阶段(Schema)
问题5:下列由左边到右边的变形,哪些是因式分解?为什么?
(1)(a+3)(a-3)=a2-9;
(2)m2-4=(m+2)(m-2);
(3)a2-b2+1=(a+b)(a-b)+1;
(4)2mn+2mr=2m(n+r);
(5)(y-3)2=y2-6y+9;
(6)ax+ay=a(x+y).
追问:结合问题5,你能说出因式分解的特征吗?因式分解与整式乘法有什么关系?(学生交流后,用PPT或黑板展示如下图畫,如图7、图8所示)
师生活动:教师出示问题,学生独立思考后交流展示. 学生展示时,要说明判断的理由;师生评议并修正,结合概念中关键词的含义,共同归纳出因式分解的特征,明确因式分解与整式乘法之间的关系.
设计说明 出示6个关系式,结合正反例,通过问题辨析,引导学生结合因式分解的概念,分析概念中关键词的含义,整体把握因式分解的本质特征,帮助学生明确:因式分解的对象是多项式,分解的结果是整式的积的形式;同时通过PPT或黑板展示因式分解与整式乘法的关系图,助力学生理解“因式分解与整式乘法互为逆变形”,可以逆用乘法公式验证因式分解是否正确,进而达到巩固概念的目的,在认知上形成心理图式.
学生掌握数学概念,不能依赖死记硬背,应以理解为基础,而理解又以经历为基础. 基于APOS理论的“概念学习四阶段”进行数学概念教学设计,能够较好地让学生经历概念的形成过程,感受数学的整体性,符合学生的认知结构和认知规律,有利于学生理解概念.
参考文献:
[1]章建跃. 数学教育随想录[M]. 浙江:浙江教育出版社,2017.
[2]中华人民共和国教育部. 义务教育数学课程课标(2011年版)[S]. 北京:北京师范大学出版社,2012.
[3]张敏,李军,孙迪. 基于APOS理论下数学史融入一元二次方程概念教学设计[J]. 数学教学通讯,2019(35).
