用于微位移测量的迈克尔逊激光干涉仪综述

王 冬, 崔建军, 张福民, 闵帅博, 陈 恺

(1.天津大学 精密仪器与光电子工程学院,天津 300072； 2.中国计量科学研究院,北京 100029；3.浙江理工大学 纳米测量重点实验室,浙江 杭州 310018)

1 引 言

迈克尔逊干涉术测量微位移可实现纳米甚至更高的分辨力,并且具备能直接溯源至激光波长等诸多优点,是目前微位移测量的重要技术手段。

1881年美国的物理学家迈克尔逊提出迈克尔逊干涉技术,用以进行以太漂移实验。后经改进发展,可以用于测量微小位移等。迈克尔逊干涉仪还是许多现代干涉仪的原型[1],其中许多干涉仪已经达到纳米级测量的精度,然而非线性误差又往往限制了干涉仪向更高精度的发展。

本文首先对迈克尔逊激光干涉仪的测量原理和非线性误差的主要影响因素及测量方法进行简单的阐释;再对目前几类针对非线性误差进行处理的改进型高精度迈克尔逊干涉仪进行介绍和分析。

2 迈克尔逊激光干涉仪及非线性误差

迈克尔逊干涉仪是一种分振幅干涉装置,即能够让一束光投射到2种传输介质分界面上时,一部分光透射,一部分光反射的装置[1]。最初的装置有2块厚度均匀、折射率相同的玻璃板,其中1块有一面镀了1层很薄的银,用于实现分振幅,产生2路光束。这2束相干光的光程不同,因此可以在接收处产生一定的干涉条纹。许多高精度的现代激光干涉仪就是在经典的迈克尔逊干涉仪的基础上发展而来的。目前,主流的商用激光干涉仪以雷尼绍公司生产的单频激光干涉仪和安捷伦公司生产的双频激光干涉仪为主。

单频激光干涉仪也称为零差干涉仪,具有精度高、稳定可靠, 且相对成本较低等特点[2]。它主要通过探测相位的变化来计算位移,其光路原理图如图1所示[3]。干涉仪工作时,激光器发出的光经分光镜BS分别进入参考镜R和测量镜M,参考镜R固定不动,测量镜M移动,参考光与测量光汇合后射入探测器D中,处理可得到相位与位移之间关系。相位与位移关系式[4～6]：

φ=4 π λ-1L

(1)

式中：φ为相位值；λ表示激光波长；L表示待测物体的位移信息。

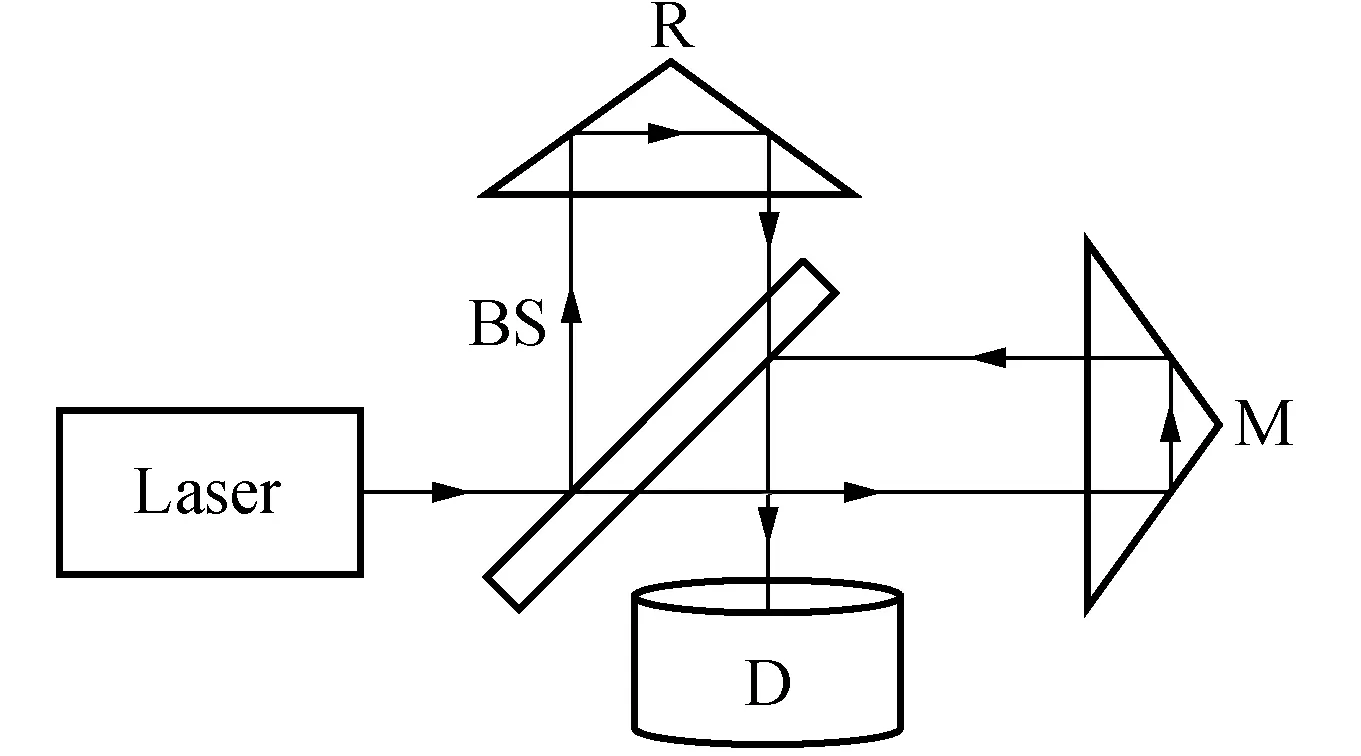
图1 单频激光干涉仪光路原理图

单频激光干涉仪容易受光功率变化、环境波动等因素的影响产生误差,为了解决单频激光干涉仪直流漂移的问题,相关学者研制了双频激光干涉仪。

双频激光干涉仪也称外差干涉仪,具有测量精度高、噪声小、动态范围宽等优势[7]。它采用双频光源使得输出信号变成为交流信号,直接消除了单频激光干涉仪因直流漂移产生的误差,提高了抗干扰能力,图2为基本的外差干涉仪原理图[8]。图中D1和D2为探测器,PhD为鉴相器。外差干涉仪的测距原理一般也是测量相位,思路与单频激光干涉仪相同,通过相位变化计算位移,其基本计算公式为[4]：

(2)

式中:N表示被测位移L中含λ/2的整数倍,即大数；ε表示不足λ/2的部分,即小数。

由公式(2)可以看出,相位细分和整数小数部分结合的精度,都会影响干涉仪的测量结果。

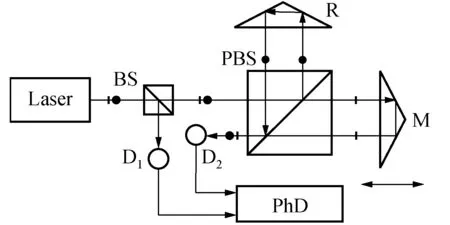
图2 外差干涉仪测量原理图

在实际应用中,激光干涉仪的测量结果往往受到多种因素影响,比如激光源波长的波动、环境变化、气流扰动、光学细分、光电探测器及后续处理电路对原始信号的处理等,都会使测量结果有所偏差,其中周期性的非线性误差幅值可达几nm,是影响整个测量系统精度的主要误差,其影响因素还包括非理想的激光源,使出射光不再是线偏振光；偏振分光镜、波片等光学元件性能不理想,也会使相位混叠产生误差;光学元件在安装调整时存在误差,如干涉光偏振轴与偏振分光元件分光轴不匹配、波片位置不精确,以及透射光学元件引起的剩余反射(也称“鬼点反射”)和光束在系统各折射面之间多次反射、散射引起的寄生反射等,这些因素均会引起相位混叠,导致一个随测量长度变化,以半波长为周期的非线性误差的出现[9～11]。

非线性误差的测量与分析对激光干涉仪品质的评价十分重要,国内外学者提出过许多测量非线性的方法,主要分为双相位测量法[12]、频谱分析法[13]、椭圆拟合法[14]、对比比较法[15]等。其中,双相位测量法不需要额外的参考量,且可直接测量非线性误差,应用广泛。其原理图如图3所示[16]。图中BD为检偏器。

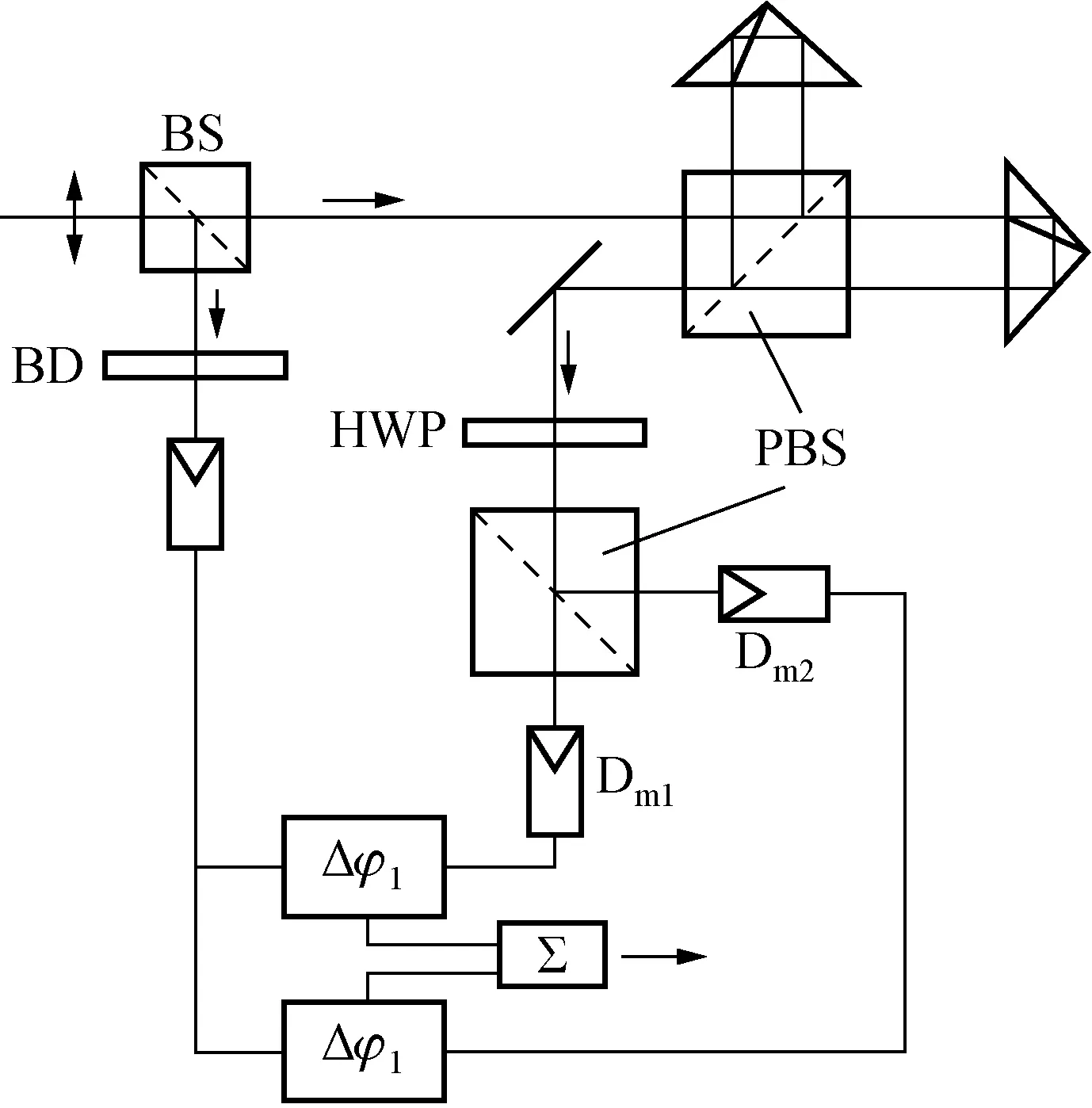
图3 双相位测量法原理图

该方法利用一个1/2波片HWP和偏振分光镜PBS,将测量信号分成2路,采用2个光电探测器Dm1和Dm2分别接收2路测量信号,2个探测器探测到的信号的相位差为:

Δφ2-Δφ1=γ+γ′+ε+ π

(3)

式中：ε为光电转换引起的固定相移； π 为初始相位差；均不会对测量结果产生影响。因此,非线性误差为:

γ+γ′≈2αsinΔφ

(4)

该方法利用差分检测的方式,使得两路信号中相移相同的部分相互抵消,只测量非线性误差的大小,但缺点是只能进行静态的测量,无法对目标运动过程中的干涉仪误差进行实时测量。

3 改进的高精度迈克尔逊激光干涉仪

目前商用的干涉仪分辨力通常在nm级,为了满足测量需求,学者们从不同的角度出发,提出了不少减小非线性误差以提高干涉仪测量精度和分辨力的方法。

3.1 采用空间分离的光路的干涉仪

一些学者采用空间分离的方法来实现非线性误差的消除,即将外差激光干涉仪中两个频率的光从空间上分离开,以此消除偏振分光镜PBS漏光而引起的非线性误差。2000年,美国国家标准技术研究院(NIST)Lawall J等[17]设计的外差干涉仪利用了空间分离的方法,在1 mm的测量范围内仍可实现10 pm的准确度,其原理图见图4。其中：QWP为1/4波片；AOM为声光调制器。该光路设计不对称,测量结果易受环境因素影响。

2004年,Wu C M[18]设计了完全对称的防止混频的外差干涉仪,周期非线性误差小于40 pm，其原理图如图5所示。图5中：FSU为移频单元；SS为直线度传感器。

图4 非对称的空间分离外差干涉仪

图5 干涉仪配置概略图

图6 新型光纤耦合的Joo-type干涉仪

利用光纤传导可以减小光学准直和系统热源对测量结果的影响,但光纤传输也会引起漂移,加剧干涉仪的周期非线性误差。2011年,罗彻斯特大学Ellis J D等[19]设计了一种光纤耦合的Joo型干涉仪,原理图如图6所示。用声光调制器AOM得到2个不同频率的激光,在形成参考光后再进入保偏光纤PMF进行耦合,消除了光纤传导引起的漂移,利用频谱分析法对干涉仪的进行测量,未检测到明显的非线性误差。图6中FC代表光纤耦合器。

2012年,德国联邦物理技术研究院(PTB)Weichert C等[20]研发了一种新型光学外差干涉仪,原理图如图7所示,其中,NPBS为非偏振分光镜；λ/2为半波片。其采用了一种利用平面平行板和空间分离的输入光束来减小周期非线性的新方法,且具有双路干涉仪的分辨力,可补偿反射镜和干涉仪光学元件之间可能的角度变化,参考臂和测量臂之间的路径差最小。实验采用对比比较法,通过与X射线干涉仪的比较来表征非线性,假设X射线干涉仪没有误差,认为非线性是测量位移与最佳拟合线的偏差,测量结果表明该干涉仪的非线性误差小于±10 pm。

图7 新型光学外差干涉仪原理图

2016年清华大学研究团队[21,22]利用空间分离的干涉方案设计了一种可实现跨尺度测量具有亚nm分辨力的双频绿光干涉仪,其实验装置如图8所示。其中：C为准直器；AP为小孔；CL1和CL2为耦合棱镜；FP为光纤接口。通过补偿光纤和声光调制器的相位噪声,使用高精度的相位计数器等方式实现了100 mm量程内,测量不确定度达到0.3 nm。

图8 双频绿光干涉仪实验装置图

3.2 改善光学器件装配的干涉仪

光学器件的装配也是造成非线性误差的因素之一,许多学者沿着这一方向展开了对减小非线性误差的研究。

2009年韩国Ahn J等[23]将波片的快轴调整到一个特殊的角度,补偿了偏振分光镜造成的非线性误差,将其缩小到0.36 nm,光路原理见图9，其中：HWP为1/2波片；QWP为1/4波片；D为光电探测器。

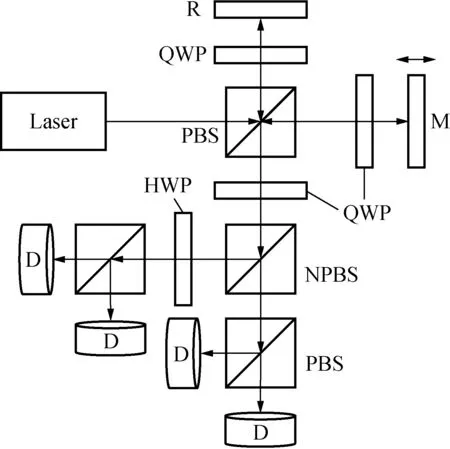
图9 测量光路原理图

2011年Pozar T等[24]移除多个波片等能引起非线性误差光学器件,简化了光路,原理见图10。图中：激光器发射45°的线偏振光,M和R分别为测量镜与参考镜,OWP为1/8波片,PZT为压电陶瓷驱动器,SG为触发信号,PDx和PDy为光电探测器。

图10 简化的单频干涉仪

2012年侯文玫等[25]基于调整光学器件补偿相位变化的思路设计了一套减小非线性误差的外差干涉仪,如图11所示。图中： PM和PR为偏振片；DM和DR为光电探测器；IM和IR为光电探测器转换后得到的光强。

图11 外差干涉仪非线性补偿消除光路原理图

在偏振片PM前加上1/4波片QWP,使得参考光与测量光合成一个旋转的线偏振光,通过旋转偏振片PM,调整其检偏轴位置就可改变旋转线偏振光与参考光的相位差,这个相位差就可以用来补偿产生非线性误差的相位差,使其成为常数,从而减小干涉仪的测量误差。

2016年Cui J等[26]基于简化光路的思想,尽量减少使用波片,多采用消偏振分光镜和沃拉斯顿棱镜,将非线性误差控制在0.2 nm之内。不过,前面的几种调整角度的方法都需要精确测量,安装调试过程比较复杂,而且单频干涉仪的抗干扰能力不强,因此还没有这些方法的商业应用实例。

3.3 激光合成波长干涉仪

2014年浙江理工大学陈本永研究团队[27,28]研制了激光合成波长纳米测量干涉仪,其测量分辨率达到0.02 nm,在测量范围为mm级时的非线性误差依然小于2 nm。激光合成波长纳米测量干涉仪是一种通过测量相对较大的位移来间接测量纳米级别位移的装置,其主要工作原理如图12所示。

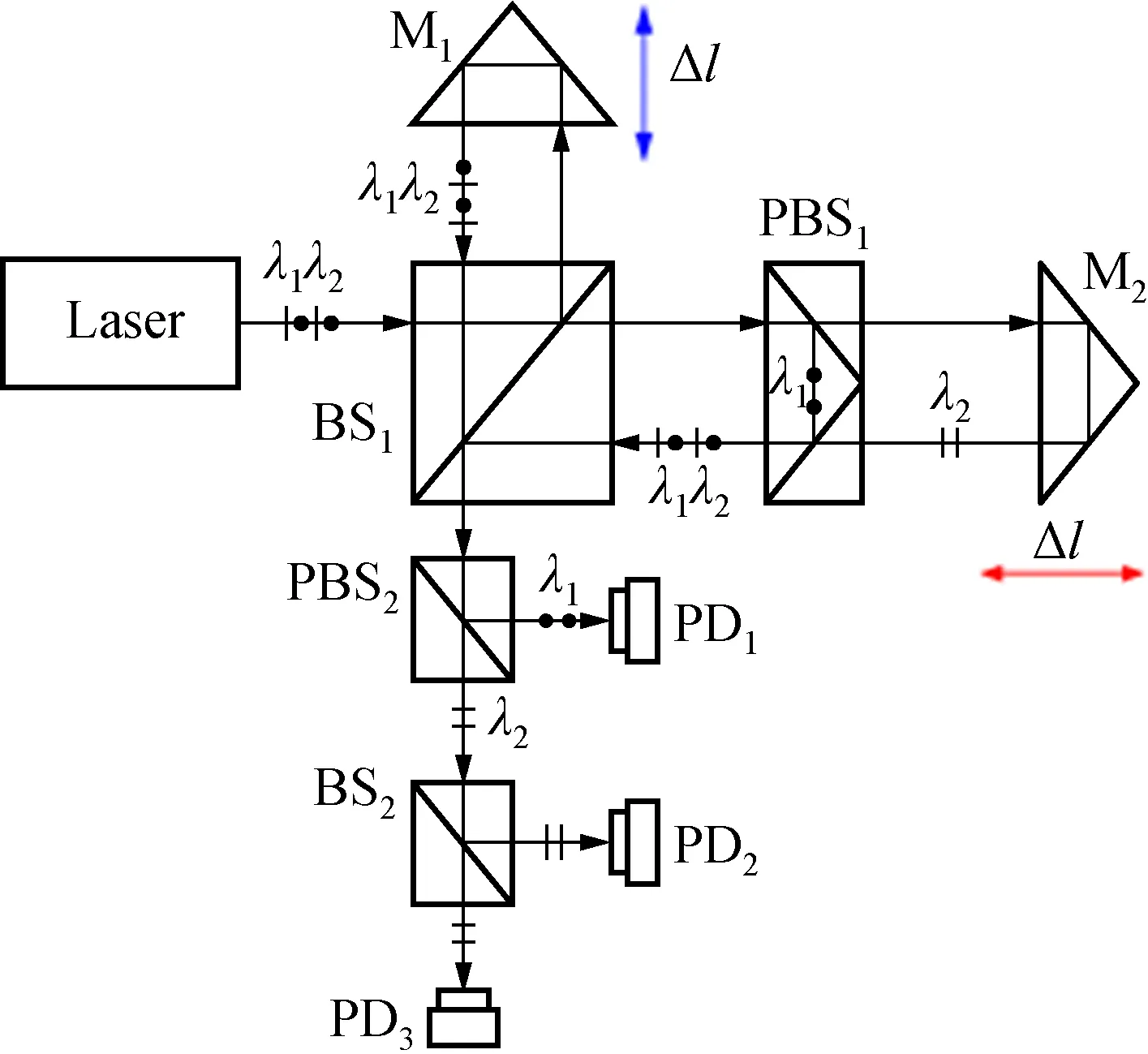
图12 激光合成波长纳米测量干涉仪原理图

图12中：PD为光电探测器；M1和M2为反射镜；BS为分光镜；PBS为偏振分光镜。波长分别为λ1和λ2的两路干涉信号相位差为

Δφ=4 π (L/λs+LM/λ2)

(5)

λs=λ1λ2/|λ1-λ2|

(6)

式中：λs表示合成波长,这是一个“虚波长”,与光源信号的频差有关,通过计算获得；L表示参考光程差；LM表示偏振分光镜PBS1到测量镜M2之间的光程。

当测量镜M2发生一个微小位移Δl,势必会引起两路信号相位差的改变,这个变化可以通过将参考镜M1移动一定的位移ΔL进行弥补,将相位差变为

(7)

为了保持相位差恒定,有Δφ=Δφ1,得到关系式

(8)

激光合成波长干涉仪选用频差较大的光源时,可得到远高于一般干涉仪的细分系数,大幅度减小了因光学细分产生的误差,提高了测量结果的精度。

3.4 采用光学多倍程干涉技术的干涉仪

2007年候文玫等[29]提出了一种可以减小激光干涉仪的非线性误差的理论方法,其核心公式推论如下：

(9)

式中：Δlm为测量位移长度；N1表示光程倍数；Δφ表示理论干涉相位差；γ则表示非线性相位误差。简单总结就是增加光程倍数N1可以有效的减小非线性误差。此外,除了提高干涉仪的测量精度外,提高干涉仪的分辨率也是提高干涉仪品质的一个方向,光学倍程法可以有效提高条纹细分的倍数,也会在一定程度上减小光学细分所带来的误差,提高干涉仪的分辨率,因此有许多学者对此进行了研究。

2009年意大利计量研究院Pisani M等[30]使用2块平面镜,利用一定的角度关系使得光束在两个平面镜之间来回反射以达到多倍程的目的,分辨力达到了0.4 nm。但由于反射模式会产生横向偏移,这种方法不足以进行长距离测量。多倍程的零差激光干涉仪原理图如图13所示。

图13 多倍程的零差激光干涉仪原理图

2010年韩国Lee J等[31]则是让光束在2个直角棱镜中来回反射,预计在21倍的细分倍数下可以实现8.7 pm的分辨率,其光路图如图14所示,其中,RP为反射棱镜。

图14 一种多倍程干涉仪

4 现有问题及发展趋势

激光干涉仪由于其可溯源的优点广泛地应用于计量以及其它科研或工业测量中,而以迈克尔逊干涉仪为基础发展的各种干涉仪器提高了测量精度和测量范围。根据对目前多种迈克尔逊干涉仪的研究现状的调查,其主要问题在于各种因素引起的非线性误差,限制了这类干涉仪的精度往亚nm级的提高。这些因素包括以下几点：不理想的光学元件引入的非线性误差,例如偏振分光镜的分光不完全引起两束线偏振光的非正交或者波片对偏振光偏振态的影响等；电子细分相位时产生的周期性的误差；激光传输或者反射过程中的光损失；激光光源本身的初始偏振误差等。

由于目前光刻机、芯片制造等产业存在技术需求,激光干涉仪的测量精度还需要进一步提升至亚nm级甚至pm级。因此,激光干涉仪可预想未来的发展趋势有以下几点：

(1) 迈克尔逊干涉仪的测量精度受到非线性误差的制约,在目前的各种减小非线性误差的方法下,一些干涉仪已经可以把这种周期性的非线性误差控制在亚nm级,在一定程度上提高了干涉仪的品质,但大多依赖于实验室环境,难以在工业生产等实际场景中大规模推广应用,因此继续寻找更有效的方法或者在原理上改进以提升高精度干涉仪的实用性可能成为一个趋势。

(2) 发展其他类型的干涉仪。例如Fabry-Perot干涉仪,基于多光束干涉的原理,测量多光束谐振产生的干涉条纹极值所对应的激光频率变化来计算谐振腔位移,理论上具有pm量级的精度,不过由于测量范围小、实际精度不够高等问题限制了它的应用。这类干涉仪由于原理上的不同,没有电子细分之类的非线性误差,具有一定的发展潜力,因此也是干涉仪发展的趋势之一。

(3) 目前高精度的激光干涉仪在减小非线性误差方面进行了诸多研究并取得了效果,对于非线性误差达到亚nm甚至pm级的干涉仪而言,其他来源的误差,比如激光光源的波动、电噪声干扰等一些非周期性的误差反而成了制约干涉仪实际使用中精度的主要误差,在这种情况下单一减小周期非线性误差未必能够提高干涉仪的实际品质,因此结合使用激光干涉仪在信号处理等其他方面对非周期性的误差进行研究补偿也是一个方向。

(4) 针对激光干涉仪中非线性误差的测量方法多种多样,但由于测量结果无法溯源,采用不同方法进行所得的结果也难以进行比较,无法判断干涉仪实际的误差情况,因此,提出一种通用的可溯源的激光干涉仪误差测量方法也非常重要且迫切。