基于天牛须改进粒子群算法的平面度误差评定研究

刘 超， 王 宸，2， 钟毓宁

(1.湖北汽车工业学院，湖北 十堰 442002；2.上海市智能制造与机器人重点实验室，上海 200072)

1 引 言

随着精密制造技术的不断发展，有效、准确地评定平面度误差具有重要的现实意义。在相关的国际标准和国家标准中，评定平面度误差的方法主要有：最小区域法(minimum zone method，MZM)、最小二乘法(least square method，LSM)及智能优化算法等。MZM评定平面度误差可以得到理想误差值，但是寻找最小区域相对耗时，不能满足现代工业测量的高效需求[1]，因而目前采用最小二乘原理的三坐标测量机(CMM)测量平面度时，不能满足最小区域条件，这使得测量的评定结果难以满足实际情况[2]，由于CMM成本的限制，CMM获取的测量样本数量有限，费兰等[3]采用空间插值方法，获取更准确的平面度误差估计。康岩辉等[4]介绍了一种基于多角度旋转的全面形测量方法，该方法使用波前分离技术，得到相对较低的平面度的绝对误差值。随着群体智能优化算法的发展，各种新型算法不断涌现，改变以往算法复杂度较高且计算耗时等问题。

Chakraborti N等[5]提出了一种基于遗传算法(genetic algorithm，GA)的平面度误差求解算法，建立了完全满足最小区域条件的平面度评价数学模型，通过仿真计算和实验数据验证了该算法的有效性，表明该算法具有全局优化和快速收敛的特点。温秀兰等[6]提出了基于实数编码的遗传算法平面度误差求解算法，通过三坐标测量机测量的实际数据进行验证，取得了更优效果。罗钧等[7]提出将改进人工蜂群算法(modified artificial bee colony, MABC)用于平面度误差最小区域的评定，该算法在基本人工蜂群算法(artificial bee colony, ABC)模型的基础上引入两个牵引蜂和禁忌搜索策略。通过实验验证了该算法在优化效率、求解质量和稳定性上均优于ABC算法，但是该算法的后期的收敛速度慢。刘浩然[8]等针对粒子群算法易陷入局部最优的问题，提出了基于雁群启示的扩展粒子群算法( an improved extended PSO algorithm based on geese flight，GeEPSO)，该算法融合了所有粒子的个体极值信息，同时提高了种群多样性。毕立恒等[9]基于分群粒子群算法(grouped particle swarm optimization algorithm, GPSO)对平面度误差进行了研究。在不增加粒子的数量和维度的情况下，使用两个粒子群分别进行全局搜索和局部搜索，实验结果验证该算法具有较强的优化能力，评定精度较高，但是粒子群算法(particle swarm optimization algorithm, PSO)的局部搜索能力相比于天牛须搜索算法(beetle antennae search algorithm, BAS)较弱，会使得GPSO算法的整体寻优效率降低。

针对上述问题，本文设计基于天牛须改进粒子群算法(particle swarm optimization algorithm based on beetle antennae search algorithm, BAS-PSO)，按最小包容区域法来建立平面度误差评定数学模型，PSO算法用于全局搜索，BAS算法用来局部寻优,提高了搜索效率，实例验证结果表明:本文算法具有较强的优化能力，评定精度较高。

2 空间平面度误差的数学建模

根据最小区域法对平面度误差的评定，本质上是找到两个理想的平行平面，这两个平面包含要测量的实际平面并且具有最短的距离，这是非线性最优化问题。

设平面上的测量点为Pjk(x,y,z),j=1,2,…,m;k=1,2,…,n，其中m、n分别为x和y方向的分段数，由最小包容区域确定的公式(1)和各测点相对于最小包容平面的偏离量公式(2)[10]，得到平面度误差公式(3)。

z=ax+by+c

(1)

(2)

f=Dmax-Dmin=

(3)

因为a,b=1[10]，所以

(4)

故求解平面误差就转变为寻求a,b的值，使目标函数f为最小。所以适应度函数为

fitness(i)=1/[0.001+f(i)]

(5)

其中，

(6)

根据函数性质，满足最小条件的平面度误差的适应度函数fitness是二维空间上的凸函数，并且具有唯一的全局极小值[11]。本文根据平面度误差评定最小原则，设计BAS-PSO来求解目标函数的最优解。

3 求解算法

3.1 BAS-PSO算法

BAS是根据天牛觅食原理开发的算法。当天牛根据食物气味来寻找食物时，天牛有2只长触角，如果右边触角收到的气味强度高于左边，则往右搜索食物，反之亦然[12～14]。该算法具有全局搜索速度快、求解精度高等特点。

PSO是一种模拟鸟群的捕食行为的优化算法，其特点是程序简单、易实现。通过记录每个位置的适应度来确定个体极值pbest和粒子群体的极值gbest，较快地找到全局最优解，并由此来调整自己的位置与速度[15～17]。虽然PSO算法在局部搜索速度上更有优势，但是由于缺乏粒子速度的动态调节，算法运行到后期收敛速度较慢，求解精度不能达到要求，容易陷入局部最优。

本文BAS-PSO算法使用局部搜索能力较强的BAS算法，在算法前期快速逼近目标函数的适应度值，为粒子的速度和位置调节提供自主寻优的能力，从而快速得到全局最优解。目标函数的适应度值计算如下：

Fleft=f(xL)

(7)

Fright=f(xR)

(8)

式中：f(xL)和f(xR)分别为天牛左须、 右须目标函数值。

适应度函数值越低则表明：实验所测平面度误差越低，故通过设计比较函数获取个体极值pbest和群体极值gbest：

pbest=min(Fleft，Fright)

(9)

gbest=min[pbest(1)，pbest(2)，…，pbest(i)]

(10)

在每次循环后都进行个体极值和群体极值的及时更新。当个体极值或者群体极值确定时，PSO的速度和位置也做相应的调整。

更新速度公式为

vi(t+1)=vi(t)+c1r1(pbest(i)-xi(t))+

c2r2(gbest-xi(t))

(11)

更新位置公式为

xi(t+1)=xi(t)+vi(t+1)

(12)

式中：vi(t)和xi(t)分别为第i个粒子t时刻的速度和位置;c1和c2是学习因子；r1和r2是介于(0，1)之间的随机数。

这样利用BAS算法与PSO算法进行结合，可以充分发挥PSO的全局搜索能力，同时也能够发挥BAS算法的局部搜索能力，使得两种寻优算法在优势上进行互补，可以大大提升算法的搜索性能。

3.2 算法步骤与流程

具体步骤如下：

Step1：初始化各项参数，包括：种群大小np，初始步长step，学习因子c1、c2，最大和最小惯性权重ωmax、ωmin，最大和最小速度Vmax、Vmin，最优值条件dmax、dmin，迭代次数n，在(0,1)之间来保证粒子群的随机性所设置的随机数r1、r2，随机初始解x。

Step2：计算天牛左须坐标为

xL=X+d0·dir/2

(13)

计算天牛右须坐标为

xR=x-d0·dir/2

(14)

其中dir=rand(0,1)为(0,1)之间的随机数。

Step3:通过式(7)和式(8)计算须的气味强度(即函数适应度值)。

Step4:通过式(9)和式(10)获取个体极值和群体极值gbest。

Step5:判断是否达到迭代最优值条件，若是则终止，否则进入Step6。

Step6:通过式(11)和式(12)更新群体的速度和位置，主导粒子向全局最优靠近。

Step7:判断是否达到最大迭代次数，若不满足，则转向Step2，否则跳出循环，输出最优解。

函数流程图如下：

图1 算法流程图

4 实验验证

4.1 性能测试

为了验证BAS-PSO算法的有效性，本文中选用二维Rosenbrock和二维Schaffer作为测试函数。

二维Rosenbrock函数性质如下：

(15)

最优解为f1(1，1)=0。

二维Schaffer函数性质如下：

-100≤xi≤100

(16)

最优解为f2(0，0)=0。

f1(x)是一个用来测试最优化算法性能的非凸函数，它有一个全局极小点，但它却是病态的，由于函数极小值点附近有一条弯曲而狭长的山谷，使得全局极小值点附近函数值更新极为缓慢，很难找到全局极小值，因此一般用它来评价算法的搜索性能；f2(x)是二维的复杂函数，具有无数个极小值点，由于该函数具有强烈震荡的性态，优化过程中极易停滞在这些局部极值点处，故很难找到全局最优值。

选择这2个函数作为测试函数，一是因为它们和平面度误差函数一样都有2个待优化的函数变量；二是它们都很难找到全局最优值，而且一旦陷入局部最优就很难跳出。故采用以上2个测试函数可以很好地衡量BAS-PSO算法的综合性能。

图2 Rosenbrock函数测试结果

图3 Schaffer函数测试结果

BAS-PSO算法部分参数设置如表1所示，该算法使用matlab2019a进行编程，运行于内存为8 G，CPU为3.20 GHz双核，操作系统为Windows10的高性能计算机。对以上2个测试函数，分别使用BAS-PSO，BAS和PSO进行25次实验，得到测试函数结果如图2和图3所示；迭代次数设置为50，得到各算法对测试函数的迭代图形如图4和图5所示。

表1 算法参数设置表

图4 Rosenbrock函数迭代结果

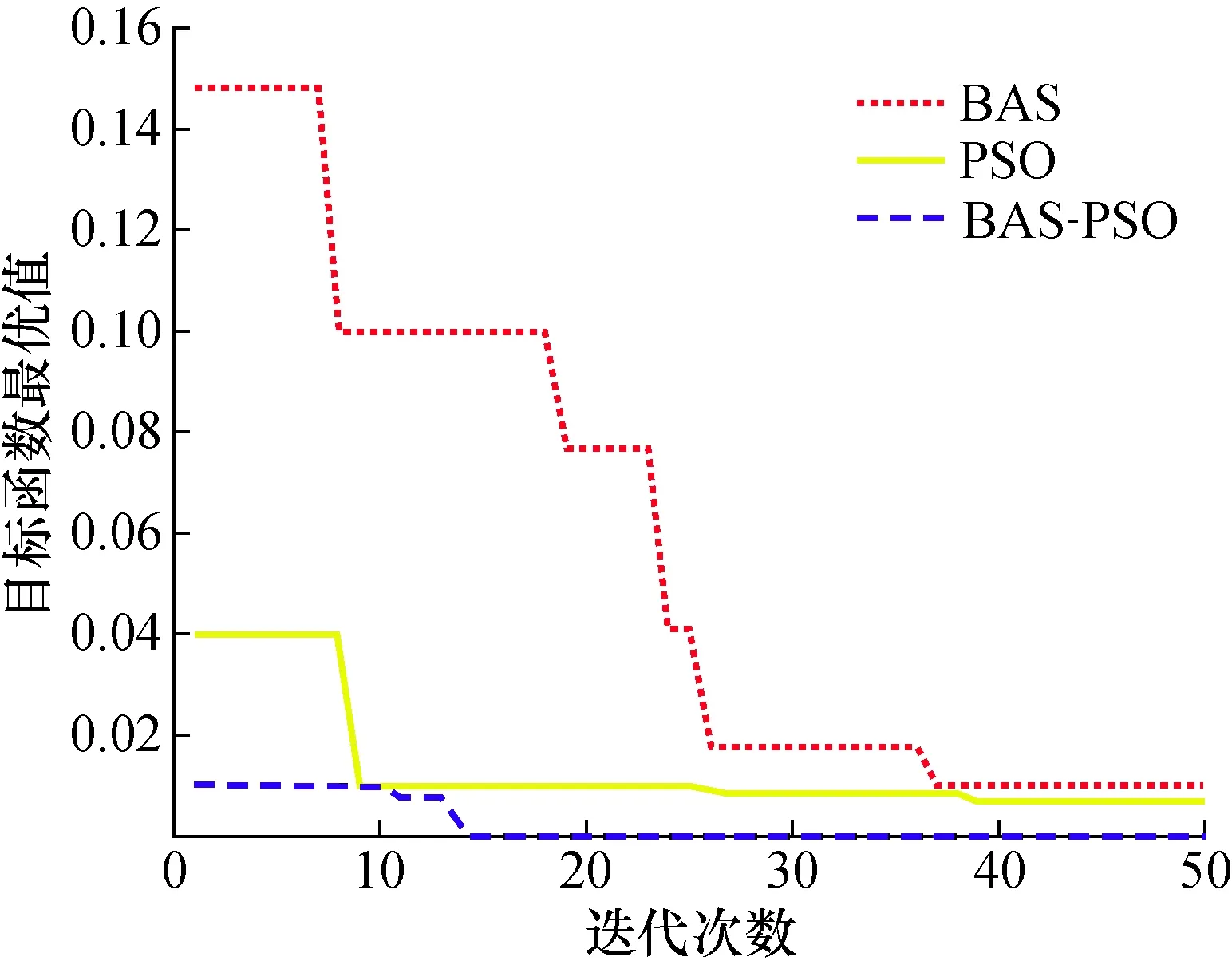
图5 Schaffer函数迭代结果

从图2和图3的性能测试结果可以得出，BAS-PSO相对BAS和PSO算法精度更高、稳定性更好。从图4和图5的函数迭代结果可以看出，BAS-PSO算法的迭代速度更快，迭代结果更逼近测试函数的最优解值，并且数据波动性比较小。综上所述，BAS-PSO相比BAS和PSO算法性能更优。

4.2 误差评定实例

采用意大利COORD3公司的ARES7三坐标测量仪对一块规格为400 mm×400 mm的一级平板进行测试，采集的受测点为50个，其采样点坐标X、Y、Z数据如表2所示。

表2 测量数据

对表2采样点数据，分别使用LSM、GA、BAS、PSO和BAS-PSO算法进行平面度测量并对比分析如图6，各算法的耗时如图7所示。

根据国家计量检定规程[10]，一级平板要求最大公差为0.009 mm,由图6的测量结果可知，本文的各算法都满足最大公差的要求，但是BAS-PSO算法的测量精度最高，为0.006 15 mm，相对LSM、GA、BAS、PSO算法测量的平面度公差值分别减少了0.002 3 mm，0.001 27 mm，0.000 58 mm，0.000 37 mm，可知BAS-PSO精度优于其他算法。从图7中各算法的耗时图可以看出BAS-PSO算法的求解用时最少，因此其求解速度较高。

图6 测量平面度误差对比

图7 各算法耗时比较

5 结 论

为了准确快速评定平面度误差，本文提出了BAS-PSO算法，对平面度误差进行了评定研究。利用Rosenbrock和Schaffer测试函数，验证了BAS-PSO算法的有效性，采用BAS-PSO算法对目标函数进行求解，结果显示该算法相对于BAS和PSO算法更具有较好的寻优效果。最后，将BAS-PSO算法应用到平面度误差实例测量中，得出了平面度公差值为0.006 15 mm，与国家规定的一级平板最大公差值的差值为0.002 85 mm,相比LSM、GA、BAS和PSO，公差值分别减少了0.002 3 mm，0.001 27 mm，0.000 85 mm，0.000 37 mm,相对比其他算法，BAS-PSO算法计算的平面度误差值与国家规定的一级平板最大公差值的差值最大并且耗时较少，验证了该算法的可行性及优越性。为平面度误差评定提供了一种新的参考方法。