一种外磁作用下球壳系统空间磁场的计算方法
2021-03-19姚振宁刘起坤周长林
姚振宁 刘起坤 周长林
(中国人民解放军战略支援部队信息工程大学,河南 郑州 450001)
静态电磁场作用下多个物体间的相互作用计算问题是一种复杂的多体耦合问题,可用于分析电流变液[1-3]、磁流变液[4,5]、复合磁性液体[6]。在低磁舰船磁性防护中,船上空心壳体铁磁设备间的相互磁化会直接影响全船磁性指标的控制,为快速分析相互磁化影响,把复杂的空心壳体铁磁设备近似等效为球壳,此时需要研究球壳间的相互磁化问题。
含有多个磁介质球壳的球壳系统在外磁场中的磁化十分复杂,这是因为被外磁场磁化的球壳会产生相互磁化,当球壳为铁磁物质时,这种相互磁化作用更强。目前,关于静态电磁场作用下多个球体间的相互耦合研究有很多,这些研究方法可以被借鉴用到外磁作用下球壳系统空间磁场的计算上。文献[7]~文献[9]在双球坐标系中求解双球静电问题,并由拉普拉斯方程获得解析解,但解析解是用积分或特殊函数来表示的,使用起来不方便。文献[10]利用正交函数法求解双球静电问题,虽然可以获得解析解,但解析解含有无穷级数。文献[11]~文献[13]利用多极矩展开法来计算电介质球间的相互作用,当介电常数较小时,计算比较方便,但如果介电常数较大,计算项数将迅速增多。文献[14]利用镜像法来计算导体球系统的偶极矩或电场空间分布,镜像法比较适合由单个或多个形状对称物体组成的系统,而且计算精度高、速度快,但一般只适用于导体球系统或介电常数足够大的电介质球系统。文献[15]推导了铁质球体间的相互磁化产生的镜像磁偶极子磁矩和镜像磁荷,并得到外磁作用下铁质球体系统空间磁场的镜像解析解,虽然镜像解析解的计算精度较高,但只适用于球体系统空间磁场的计算,不适用于球壳系统空间磁场的计算。相对于球体间相互磁化,球壳间的相互磁化更为复杂,目前还没有公开文献利用解析解来计算球壳间的相互磁化问题。
本文从外磁作用下的单个球壳与单个球体产生的磁场规律出发,通过引入磁场比例系数把球壳间的相互磁化等效为球体间的相互磁化,并根据镜像法推导出球壳间的相互磁化规律,进而求出外磁作用下球壳系统空间磁场的镜像解,并分析讨论了镜像解的计算阶数选择,最后验证了球壳系统空间磁场镜像解的正确性。当球壳为弱磁物质时,由于相对磁导率较小,球壳间的相互磁化作用不明显,所以本文研究外磁作用下铁质球壳系统空间磁场的计算。
1 球壳系统空间磁场表达式
如图1所示,球壳系统置于真空中,设球壳1(球心为O1)的内外径分别为Ri和R,球壳2(球心为O2)的内外径分别为ri和r,球心间的距离为d,球壳相对磁导率为μr,He为均匀外磁场。
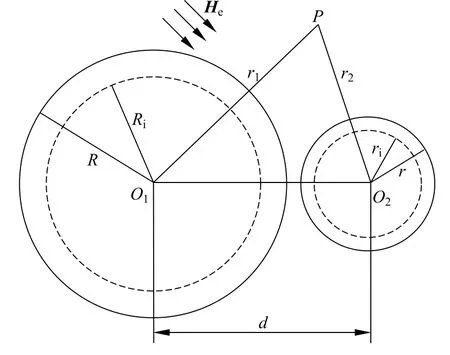
图1 球壳系统
在外磁场作用下,球壳系统被磁化,其在周围空间任一场点P产生的空间磁场表达式为

式中,H1和H2为两个球壳由于被外磁场磁化而分别在场点P产生的空间磁场;H′1和H′2为这两个磁化的球壳由于相互磁化而分别在场点P产生的附加空间磁场。H1和H2可由以下三式求出[16]

式中,m1、m2为两个球壳被外磁场磁化后的等效磁偶极子磁矩;r1、r2的方向由球心O1、O2分别指向场点P;λ1、λ2为两个球壳的磁场比例系数。
可见,求解球壳系统空间磁场的关键在于计算附加空间磁场,而附加空间磁场没有直接的解析表达式,需要通过其他方法求出。
2 附加空间磁场的镜像计算
如图2所示,设系统中球壳1(球心为O1)的内外径分别为Ri和R,球壳2(球心为O2)的内外径分别为ri和r,球壳2被外磁场磁化后的等效磁偶极子磁矩为m2=m2x e x+m2y e y+m2z e z,假定球心O1为坐标原点,并令α=(μr-1)/(μr+1)。
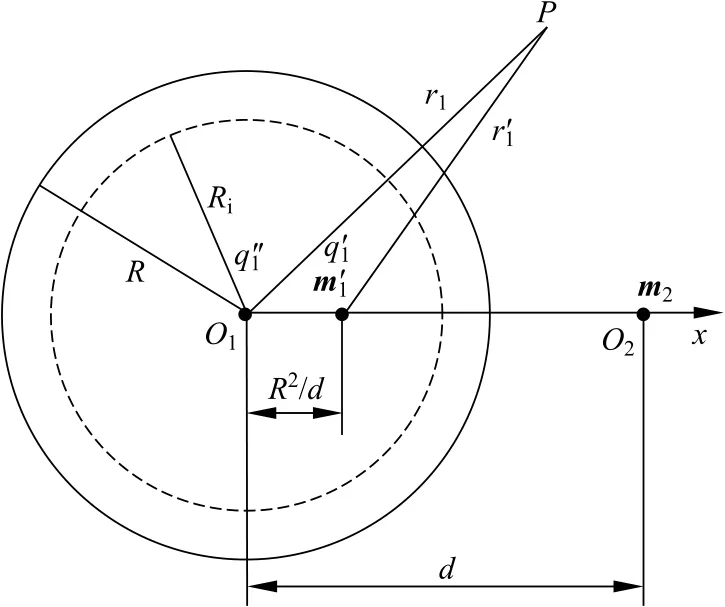
图2 球壳间的磁化
在相同均匀外磁场作用下,单个球壳与单个球体产生的磁场形式相同,仅仅相差一个磁场比例系数,所以可以通过引入磁场比例系数,把球壳间的相互磁化等效为球体间的相互磁化。根据由镜像法推导出的球体间的相互磁化研究[15],并引入磁场比例系数,则等效磁偶极子磁矩为m2的球壳2对球壳1的磁化等效为球壳1内的一个镜像磁偶极子磁矩和两个镜像磁荷,其各自表达式和位置为
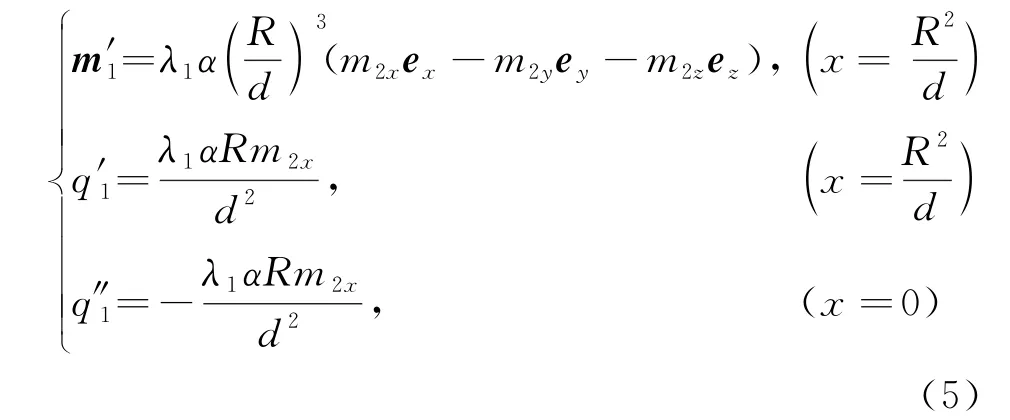
式中的磁场比例系数λ1可用式(4)第一式表示,而镜像磁偶极子、镜像磁荷产生的磁场就是球壳1的附加空间磁场
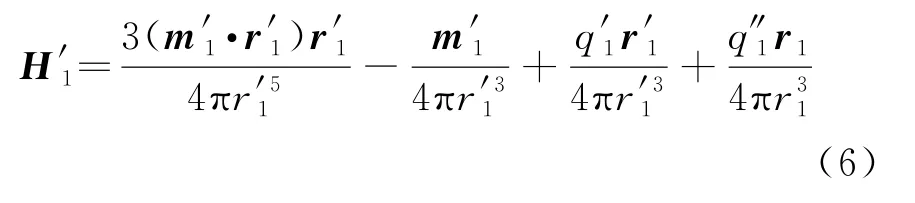
同理,如图3所示,球壳1被外磁场磁化后的等效磁偶极子磁矩为m1=m1x e x+m1y e y+m1z e z,则等效磁偶极子磁矩为m1的球壳1对球壳2的磁化等效为球壳2内的一个镜像磁偶极子磁矩和两个镜像磁荷,其各自表达式和位置为

式中的磁场比例系数λ2可用式(4)第二式表示,而镜像磁偶极子、镜像磁荷产生的磁场就是球壳2的附加空间磁场

因此,根据式(2)、式(6)和式(8)的表达式,再由式(1)即可求出球壳系统空间磁场的镜像解。
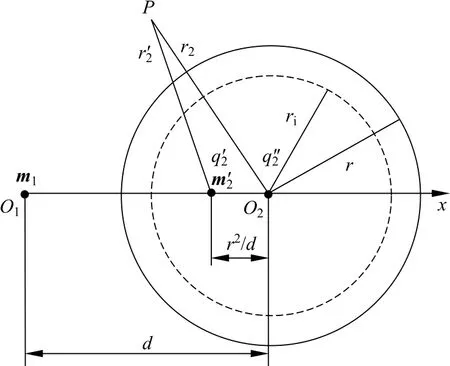
图3 球壳间的磁化
式(5)、式(6)、式(7)和式(8)分析了球壳间的一阶相互磁化,并没有考虑高阶相互磁化。仿照准静态场中各阶场分析方法,由一阶相互磁化可以获得二阶以及更高阶相互磁化(每阶相互磁化均考虑磁场比例系数),然后把各阶附加空间磁场相叠加,则可以获得较高精度的附加空间磁场。
3 计算阶数选择
为了获得较高精度的镜像解,必须考虑高阶相互磁化。当镜像解的计算阶数选择过大时,计算过程复杂;当镜像解的计算阶数选择过小时,计算精度可能不够。因此,需要合理选择镜像解的计算阶数。


图4 各阶镜像

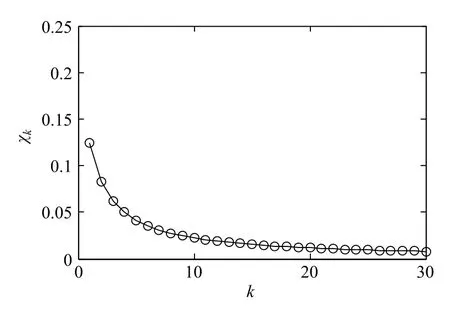
图5 极端情况下衰减程度随阶数变化曲线
由图可以看出:随着阶数增加,衰减程度逐渐减小,衰减速度逐渐变慢;当阶数到20左右时,衰减程度已经很小。实际上,在一般情况下(d>2R且μr 为有限值),由于λ<1、α<1 和(d-d i)>R,所以和的衰减速度非常快,镜像解只需考虑前几阶相互磁化即可。
4 仿真验证
为了验证本文镜像解算法的正确性,采用积分方程法计算外磁作用下的球壳系统空间磁场(剖分单元足够多),把数值解作为真解。
4.1 积分方程法数值计算
如图6所示,假设任意形状物体离散为N个单元,Q i为第i个离散单元中心(i=1,2,…,N),μr为相对磁导率,P为周围空间任一场点,He为外磁场。

图6 积分方程法数值计算示意图
首先,将场点P分别置于各离散单元中心,则可以得到以各离散单元磁场强度为未知量的线性方程组(如果外磁场是均匀的,则下式中的He(r Pj)=常数)
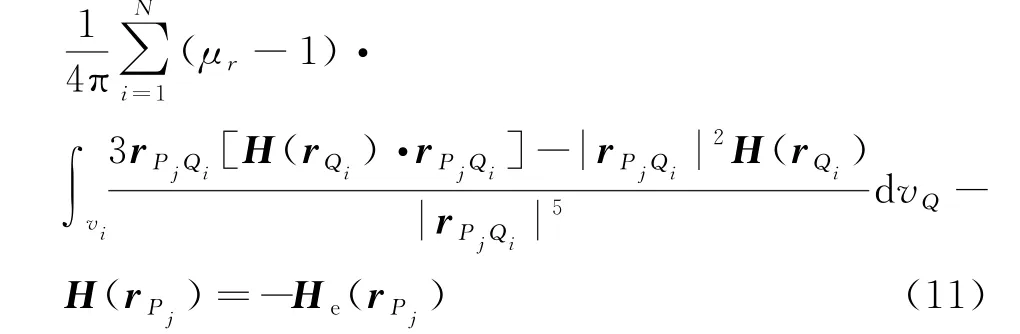
式中,j=1,2,…,N,r Qi为第i个离散单元的矢径,r Pj为第j个离散单元(即场点P)的矢径,r Pj Qi为第i个离散单元到第j个离散单元的矢径。然后,求解以上线性方程组可以得到各离散单元磁场强度。最后,代入下式可以得到外磁场作用下任意形状物体在周围空间任一场点P产生的空间磁场
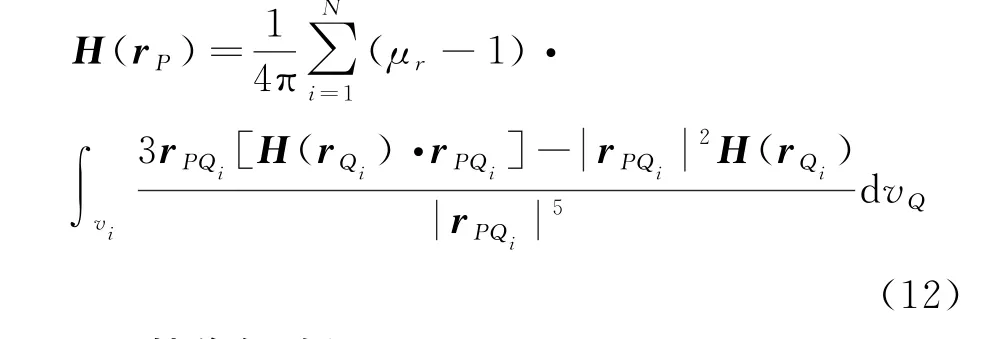
4.2 镜像解验证
如图7所示,球壳系统置于均匀外磁场Be=[33500n T,6000n T,35000n T]中,两个球壳的外径分别为R和r,间距为l,μr均为100,厚度外径比均为D。计算场点位于球壳下方的一条直线上,与x轴间的距离为2R,计算场点个数为21,镜像解的计算阶数为20。利用TrueGrid剖分软件将每个球壳进行剖分(为了清晰地显示球壳的内部轮廓,图中仅给出了球壳的下半部分),然后采用以上积分方程法求数值解。
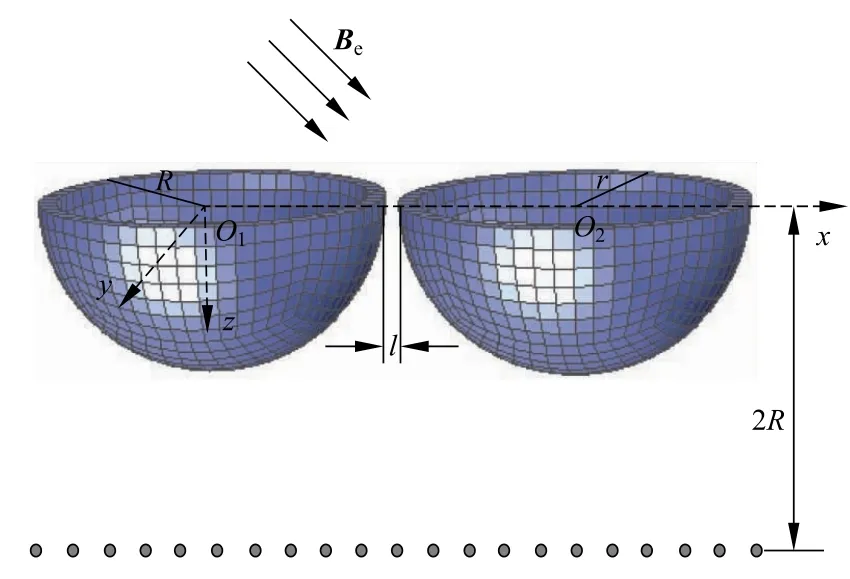
图7 球壳系统仿真实验示意图
为了评估镜像解的误差大小,本文计算了镜像解的最大相对误差er,max=emax/Bt,max(Bt,max为所有计算场点的真解最大值,emax为所有计算场点的镜像解绝对误差最大值)。为了对比检验镜像解的计算效果,本文计算了叠加解及其最大相对误差(叠加解即为不考虑相互磁化的本文零阶镜像解)。
图8和图9分别给出了r=R和R/2时场点镜像解、叠加解与真解(l=0,D=0.1)。由图可以看出:叠加解与真解吻合较差,当r=R时,其x、y和z分量的er,max分别为36.76%、15.84%和24.04%,当r=R/2时,其x、y和z分量的er,max分别为15.45%、7.35%和13.62%;镜像解与真解吻合较好,当r=R时,其x、y和z分量的er,max分别为3.31%、2.98%和3.38%,当r=R/2时,其x、y和z分量的er,max分别为3.12%、3.21%和4.03%。

图8 镜像解、叠加解与真解的比较(r=R)
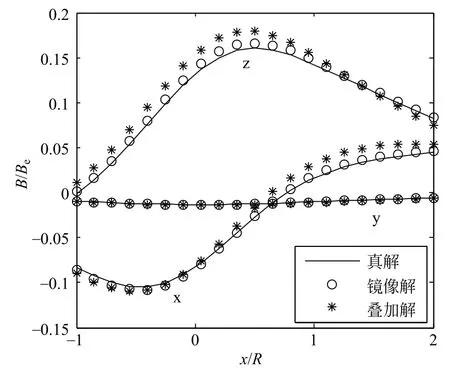
图9 镜像解、叠加解与真解的比较(r=R/2)
另外,需要考查球壳的厚度对镜像解误差的影响,图10为镜像解的er,max随厚度外径比变化曲线(l=R/10,r=R)。由图可以看出,镜像解的er,max较小,其三个分量均小于3.5%。
可见,镜像解的计算误差非常小,且适用于不同厚度的球壳系统空间磁场的计算。此外,相对于复杂耗时的数值计算方法,镜像计算把球壳间的相互磁化最终等效为镜像磁荷和镜像磁偶极子磁矩,而镜像磁荷和镜像磁偶极子磁矩具有清晰简洁的表达式,所以本文镜像解算法能够快速分析相互磁化影响。图8、图9及图10中镜像解的很小误差主要源于:为把球壳间的相互磁化等效为球体间的相互磁化,引入磁场比例系数所带来的误差;求解系统空间磁场的镜像法本身误差。
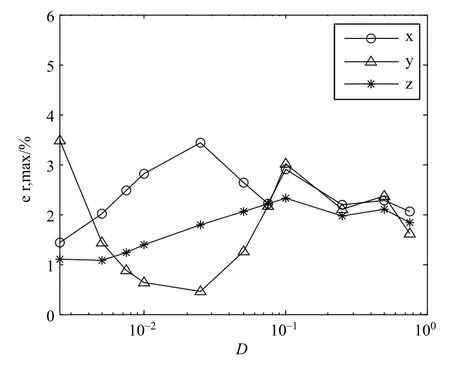
图10 镜像解的最大相对误差随厚度外径比变化曲线
5 结语
本文从外磁作用下的单个球壳与单个球体产生的磁场规律出发,引入磁场比例系数,把球壳间的相互磁化等效为球体间的相互磁化,提出一种能够计算球壳系统空间磁场的镜像解算法,最后仿真结果验证了镜像解的正确性,且适用于不同厚度的球壳系统空间磁场的计算。从整个计算过程来看,可以得到以下结论:
(1) 镜像计算把球壳间的相互磁化最终等效为镜像磁荷和镜像磁偶极子磁矩,所以只需利用镜像磁荷和镜像磁偶极子磁矩的表达式就能快速定性分析球壳间的相互磁化影响,避免了复杂的数值计算;
(2) 镜像解首先考虑每个球壳被外磁场磁化,再考虑球壳间的相互磁化,因此镜像解能够推广到含有多个球壳的系统空间磁场计算。
