基于CompactDAQ的多通道温度测量实验及COMSOL模拟
2021-03-21方奕忠崔新图白爱毓黄臻成廖德驹冯饶慧
方奕忠 沈 韩 崔新图 白爱毓 黄臻成 廖德驹 冯饶慧
(1中山大学物理学院;2物理学国家级实验教学示范中心(中山大学),广东 广州 510275)
虚拟仿真实验教学是当前物理实验教学改革的一个重要方向[1],虚拟实验和实物实验相结合的教学模式可以将理论物理、实验物理和计算物理的研究方法和理念在实验课程中融合,有效促进学生实验研究能力、创新能力和对物理知识应用能力的培养。中山大学物理实验教学中心在基础物理实验课程的力学、热学、电磁学、光学等内容分支中设置了若干虚实结合的实验模块,取得了较好的教学效果。本文将详细介绍虚实结合的热学实验模块,涉及Lab VIEW 编程、多通道数据采集系统设计、COMSOL 模拟、数学物理方程的热传导方程等教学内容。
实验模块的基本内容分为两个部分,第一部分要求学生采用四个不同阻值的薄膜电阻串联,包裹保温材料。学生自制热电偶,将测温点用导热硅胶黏贴在电阻侧表面的中间位置,串联电阻通电流升温。学生利用NICompact DAQ 机箱和NIC系列热电偶模块,基于Lab VIEW 编制多通道温度数据采集系统,测量四个电阻表面温度随时间的变化关系曲线。第二部分实验要求学生构建包裹保温材料情况下的薄膜电阻加热模型,并利用COMSOL多物理场仿真软件的固体传热模块进行模拟[2],要求调整仿真模型和仿真参数,使得仿真结果与实验结果尽可能一致,在此过程中深入学习热传导方程的相关知识。通过这种实验安排可将理论、实验和计算三种物理学的研究方法有机融合。本文对此作详细介绍。
1 电阻加热理论模型及定解问题
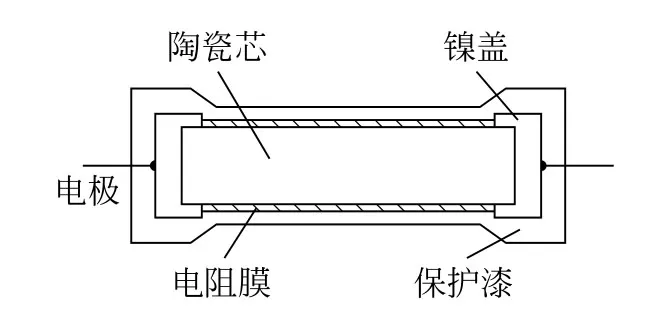
图1 薄膜电阻的结构图
实验用于加热的金属膜电阻的基本结构如图1所示。对高温有限长金属圆柱体的快速冷却问题,Heindlhofer用纯数学的方法求出了热传导方程在第三类齐次边界条件下的解析解[3],但没有考虑圆柱体内有热源的情况,故其求解的是齐次热传导方程,且没有与实验比对。Cossali研究了有限长均匀圆柱形固体的周期性热传导问题,考虑了圆柱体为多层厚板组合的情形,并进一步推广到无限厚度和无限半径的情形,但也没有考虑圆柱体内有热源的情形[4]。宿非凡等利用真空变温薄膜电阻实验仪测量了塞贝克系数随温度变化的曲线和电阻率随温度变化的曲线,得到了一般热电材料塞贝克系数和电阻率都随着温度的上升而几乎呈线性关系的结论[5]。本文作者曾研究有限长通电实心圆柱体温度分布的严格解析解及COMSOL模拟[6],将电阻简化为密度分布均匀对称的铜圆柱导体,并初步与实验进行了比较。但由于铜圆柱体模型与图1所示薄膜电阻的实际结构差别很大,故模拟结果与实验结果差别较大,本文将结合实际结构将模型改进为图2所示的三层结构,与实际电阻相比,省略了保护漆层。
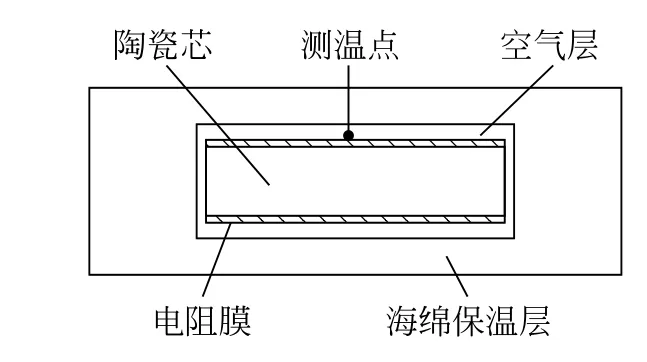
图2 薄膜电阻的COMSOL仿真模型
根据实际电阻的尺寸,设陶瓷芯为直径3.0mm,长6.0mm 的有限长均匀圆柱体,外包一层厚度为0.1mm 的电阻膜。将阻值分别为(R0,R1,R2,R3)的四个电阻串联,外面再包裹一层海绵作为保温层。海绵高30mm,宽65mm,长285mm。四个电阻沿海绵的长度方向包裹在海绵的轴线上,电阻间相距50mm。图2中只画出了一个电阻的模型,实际情况如图3所示,其中四个热电偶的感温端分别贴附在四个电阻的侧面,测量端分别连接NIC系列温度采集模块的不同通道。温度模块插在NI Compact DAQ 单槽机箱中,机箱通过USB信号线与电脑相连。实际测量时需将四个电阻用海绵紧密包裹,外部肉眼不可见。海绵与电阻的底面和侧面之间有一层空气薄层,厚度在0.01~0.50mm 之间可调。因放置热电偶探头的原因,每个电阻的空气隔层厚度不完全一样,需要根据实验结果进行调节。陶瓷芯、海绵保温层以及空气薄层的温度u均满足以下的热传导方程(1)和初始条件(2)
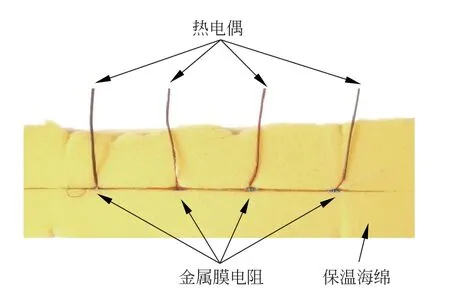
图3 薄膜电阻通电测温实验实物图
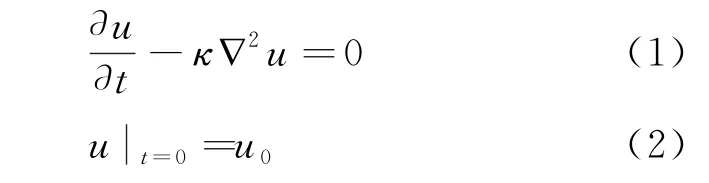
其中κ=kcρ,k、c、ρ分别为相应传热介质的热导率、比热容和质量体密度;u0为初始温度,等于外界环境的温度。电阻膜内通以电流I,则其温度u满足以下非齐次热传导方程
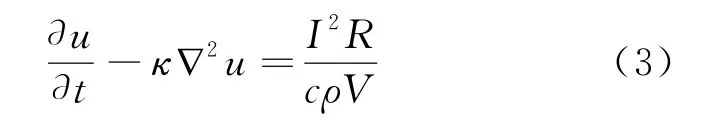
及初始条件(2)。式(3)中R为电阻膜阻值,V为体积,κ的表达式同式(1),只不过相应介质的物理量k、c、ρ改为对应薄膜材料的数值。在不同介质1、2的分界面Σ上还要满足以下两个衔接条件
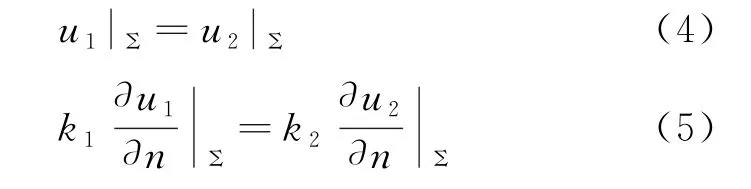
其中n的正向为垂直于界面Σ从介质1指向介质2的单位矢量方向,u1、u2分别表示介质1、2中的温度,k1、k2分别为介质1、2的热导率,即衔接条件要求界面两边的温度及热流密度的法向分量在界面Σ上均连续。在COMSOL中选定不同介质的分界面Σ就默认满足衔接条件(4)和条件(5),这样就比求解析解容易很多。可假定保温层外边界与实验室内恒温环境按牛顿冷却定律H(u|Σ-u0)交换热量,即满足以下第三类边条件
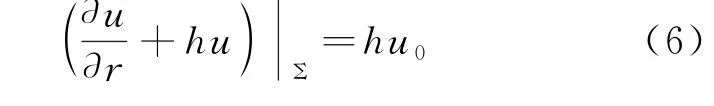
其中H为热交换系数,有h=H/k。按此模型进行COMSOL模拟。
2 实验测量
实验所用多通道温度数据采集系统采用NI-9171型USB单槽机箱和NI9211型4通道热电偶模块,基于Lab VIEW 编程实现,并采用T 型热电偶(铜-铜镍热电偶)测温。由于NI9211 内置了冷端温度补偿,故不需采用冰水混合物,方便开展实验。其AD 转换精度为24Bit,测试通道与接地端之间的隔离电压为有效值250V,避免学生实验过程中因误操作而出现安全问题。
实验中采用的四个电阻功率为0.25W,阻值分别为R0=20.02Ω、R1=42.87Ω、R2=82.49Ω、R3=100.08Ω,每个电阻侧面中间位置的温度分别用热电偶模块的CH0、CH1、CH2、CH3通道采集。四个电阻串联后,用直流稳压稳流电源供电,电压9.004V,实测电流为0.037A,四个电阻的总功率为0.333W,确保任何一个电阻的功率都不超过其额定值。用Lab VIEW 编制的数据采集程序如图4所示,可实时显示四个电阻的温度数值、温度随时间的变化关系曲线并将数据存入文件,供其他数据处理程序调用。程序的前面板图及实验结果如图5所示,图中所示曲线从下往上分别对应电阻(R0,R1,R2,R3)。加上电流后,电阻温度随时间快速上升,逐渐趋于平衡;切断电流后,温度逐渐下降至室温。在串联电路中电流相等,电阻越大,加热功率越大,平衡温度值越高。
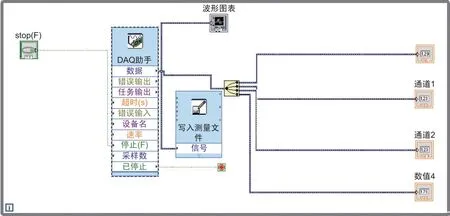
图4 多通道温度数据采集程序框图
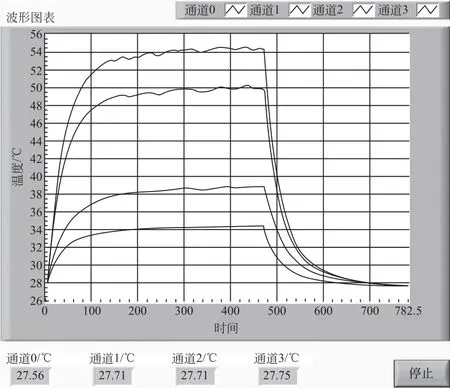
图5 程序前面板图及实验结果
3 仿真模拟与实验结果的对比
本实验采用COMSOL 的固体传热模块模拟电阻加热过程,并假设各电阻的阻值不随温度的变化而变化。电阻薄膜假设为铜膜,在COMSOL自带的材料库中,选取铜薄膜的恒压比热容为385J/(kg·K),密度为8960kg/m3,导热系数为400W/(m·K);陶瓷芯材料的恒压比热容为12000J/(kg·K),密度为3200kg/m3,导热系数为450W/(m·K);保温层恒温比热容为1700J/(kg·K),密度为25kg/m3,导热系数为0.161W/(m·K);保温层外边界与外界室温环境按牛顿冷却定律交换热量,相应地式(6)中的系数h与桌面接触的面取为20W/(m2·K),其他几个面均取为100W/(m2·K)。电阻与海绵之间的空气薄层相应的导热系数、恒压比热容及质量体密度在COMSOL里均可以自动设置,一般来说它们都是热力学温度T的指数函数,而这个函数的具体表达式由COMSOL软件根据仿真计算的精度要求自动生成。例如,COMSOL自动生成的导热系数k及恒压比热容C p的多项式近似表达式分别为
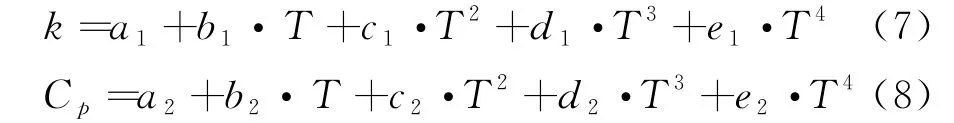
其中T为空气的热力学温度,a1=-0.0022758W/m·K,b1=1.1548×10-4W/m·K,c1=-7.9025×10-8W/m·K,d1=4.1170×10-11W/m·K,e1=-7.4386×10-15W/m·K;a2=1047.6J/kg·K,b2=-0.37259J/kg·K2,c2=9.4530×10-4J/kg·K3,d2=-6.02409×10-7J/kg·K4,e2=1.28590×10-10J/kg·K5。自动生成的密度的表达式为
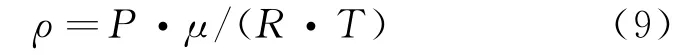
其中P为空气的压强,μ为空气平均摩尔质量,μ=0.028970kg/mol,R=8.3145J/(mol·K)。
COMSOL仿真得到的通电加热450s时的体系三维温度分布情况如图6所示,其中的电阻从左到右依次为(R3,R2,R1,R0),电阻阻值越大,温度越高,最高温度约为55℃。图7为把图6放大后得到的电阻R2表面附近温度的仿真模拟分布图。温度随时间变化关系曲线的仿真结果如图8中虚线所示,曲线从下到上分别对应(R0,R1,R2,R3),图中实线为实验结果。通电加热时间从0~470s,之后切断加热电流,让电阻保持在保温层中自然冷却。从图8可见,通电开始加热后,温度从室温27.7℃快速升高,约100s时温度趋于稳定,该趋势与本文作者之前理论上获得的圆柱体电阻模型的趋势[6]相符。470s时断电停止加热,温度迅速下降,700s后基本降为室温。除R0外,其他三个电阻表面温度随时间变化曲线的模拟值与实验值符合得很好。模拟过程中发现,空气薄层的厚度对仿真结果有一定影响,进一步仔细调节空气薄层的厚度,反复计算,可以进一步提升实验结果与模拟结果的符合度。
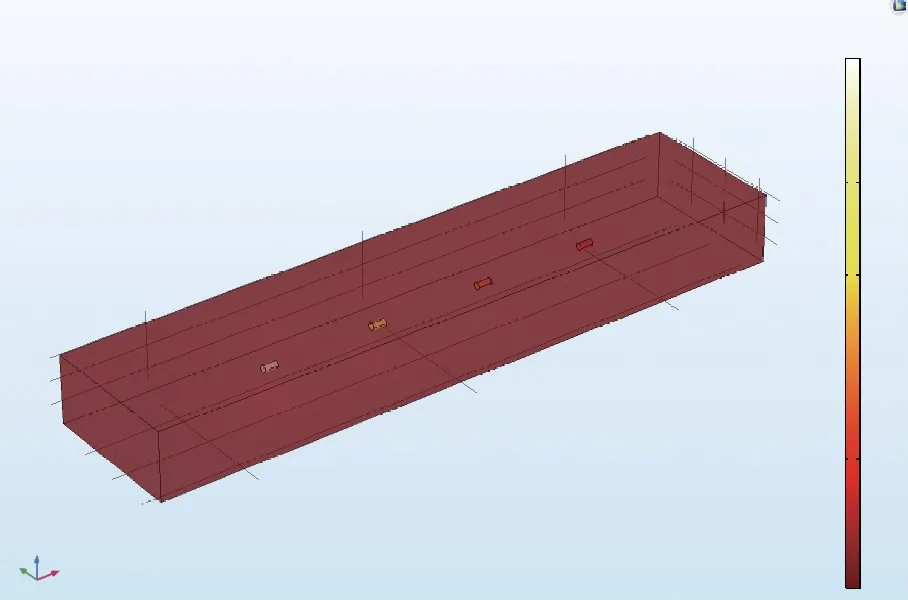
图6 三维温度分布的COMSOL仿真结果
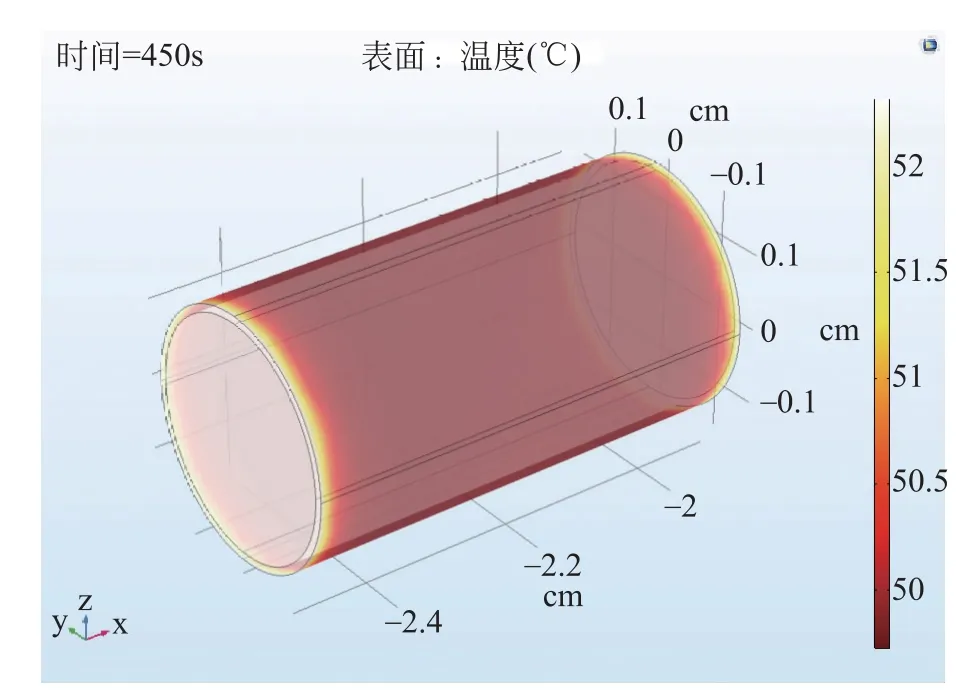
图7 电阻R2表面附近温度的COMSOL仿真模拟分布

图8 四个电阻温度变化仿真结果与实验结果对比图
为进一步提升仿真教学的效率,教师还可以利用COMSOL 的APP开发器,在课前就将电阻加热模型做成一个APP,在实验课堂上直接调用,调节仿真参数,对比仿真结果和实验结果。设计的APP界面如图9所示,从下到上分别对应(R0,R1,R2,R3)的温度T随时间t的变化关系。
4 结语
本文介绍的虚实结合实验可以在4~8学时的教学时数内,涉及Lab VIEW 编程、多通道数据采集系统设计、COMSOL 仿真、固体热传导方程等教学内容,实验内容丰富,仿真结果与实验结果符合得很好,同时为学生后续的学习、科研训练、实验竞赛甚至本科毕业论文的工作打下了较好的基础。教师在授课过程中可以根据教学时数,用仿真结果与实验结果的符合程度来界定仿真模型的难度。从最简单的具有严格解析解但符合度低的模型(将电阻看作一根通电铜圆柱体)[6]开始,逐渐过渡到无解析解但符合度高的具有多层结构的复杂模型。简单模型作为课内教学的必修内容,复杂模型可作为课外的拓展内容,为学生提供一个可持续探索的热学研究案例。
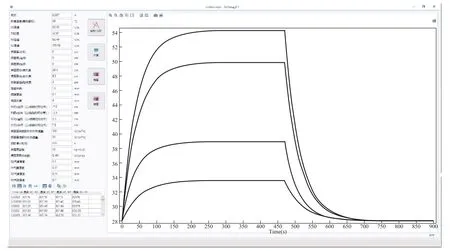
图9 COMSOL中的APP及相应的模拟曲线
