第50届国际物理奥林匹克竞赛理论试题2介绍与解答

蒋 硕 郭旭波 安 宇 张留碗 阮 东

(清华大学物理系,北京 100084)

第50届国际物理奥林匹克竞赛于2019年7月7日至15 日在以色列特拉维夫举行,共有76个国家300多名中学生选手参加。由清华大学物理系率领代表中国参赛的5名中学生全部获得了金牌[1],并取得了团体总分第一、个人总分第一,个人理论和个人实验总分第一的优异成绩。本次竞赛理论试题共三道,每道10分。其中第二道关于微波炉工作与食品加热原理的问题[2]很有意思。微波炉是大家日常生活中都用过的电器,但对它的工作原理却未必都熟悉。其实微波炉的发明就是二战时雷达研究的副产品。雷达的核心器件是产生射频电磁波的磁控管(magnetron)。在当时磁控管调试中,研究者PercySpencer发现口袋中的巧克力被加热融化,进而发明了微波炉[3]。在本次竞赛中,出题委员会将微波炉中的磁控管进行了模型简化,定性和定量地探究它的工作原理,全面考查电磁学的内容;并利用电磁波与水分子作用(受激电偶极子模型),研究微波加热食物的机制。题目贴近生活同时全方位考查基础物理知识,本文将对它进行详细的介绍与解答。

1 题目:微波炉的物理

这个题目是关于微波炉中微波的产生,及其加热食物的用途。微波是在一个被称为磁控管的装置中产生的。Part A 是关于磁控管的原理,PartB是食物对微波的吸收。

PartA:磁控管的结构与原理(6.6分)

磁控管是用来产生微波辐射的装置,可产生脉冲(用于雷达)或连续(比如在微波炉中)的微波。磁控管有一种自放大的振荡模式。对磁控管加上静态(非交流)电压可很快地激发这一模式。产生的微波辐射再从磁控管输出。

典型的微波炉磁控管由铜质实心圆柱形阴极(半径为a)和环绕它的阳极(半径为b)组成。阳极为较厚的圆柱外壳形状,并钻有多个圆柱型空腔。这些空腔被称为“谐振腔”。其中一个谐振腔连接到天线,把微波能量发射输出。在下面的题目中忽略天线。所有内部空间都在真空中。考虑图1(a)显示的一种典型的具有8个谐振腔的磁控管。图1(b)所示为单个谐振腔的三维结构。如图所示,八个腔中的每一个都表现为电感—电容(LC)谐振器,其谐振频率为f=2.45GHz。

沿着磁控管轴向施加一个静态均匀磁场,指向页面外(图1(a))。在阳极和阴极之间还施加一个恒定电压。从阴极发射的电子达到阳极使其带电,因而激发出一个振荡模式,该模式中,每两个相邻谐振腔之间的电荷的符号是相反的。谐振腔可以放大这种振荡。

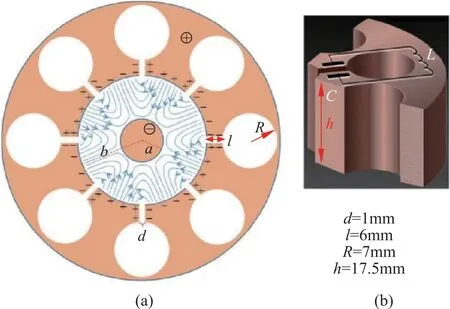
图1 磁控管简化示意图

上述过程在阴极和阳极之间产生了一个交变的电场(图1(a)中的灰线;静电场部分未画出),其交变频率为前述的f=2.45GHz。这个交变的电场叠加在恒定电压引起的静电场上。阳极和阴极之间的交变电场的典型振幅约为静电场的1/3。电子在阴极和阳极之间的运动受到静电场与交变电场的共同作用。这使得到达阳极的电子将它们从静电场获得的大约80%的能量转换为交变场。少数发射出的电子返回到阴极后释放出更多的电子,进一步放大了交变场。

每个谐振器都可认为有电容和电感,如图1(b)所示。该电容主要来自谐振器表面的平面部分,而电感来自圆柱形部分。假定谐振器中的电流均匀地沿着圆柱形谐振腔的表面流动,且该电流产生的磁场强度是理想无限长螺线管的0.6 倍。图1(b)给出了谐振器的几何参数及其数值。真空介电常数和磁导率分别为ε0=8.85·10-12F m和。

A.1(0.4分):用上述数据计算谐振器的谐振频率f。(你的计算结果可能会与题目给出的实际值f=2.45GHz不同。在下面的问题中使用题目给出的实际值。)

我们现在再来讨论磁控管的情况。阴极和阳极之间的距离是15mm。由于前述的能量的损失,假设每个电子的最大动能不超过Kmax=800eV。静磁场的强度为B0=0.3T。电子的质量和电荷分别为m=9.1·10-31kg 和-e=-1.6·10-19C。

A.3(0.4分)在一个参照系中数值估算电子运动轨迹的最大半径,该参照系中电子的运动近似为圆形,且该参照系近似为惯性系。

A.4(1.2分)图2所示为某一时刻阳极和阴极之间的交变电场线(静电场电场线未画出)。在答题纸中指出此时刻在A、B、C、D和E处的电子,哪些电子会飘向阳极,哪些会飘向阴极,哪些电子的漂移方向完全垂直于半径方向。

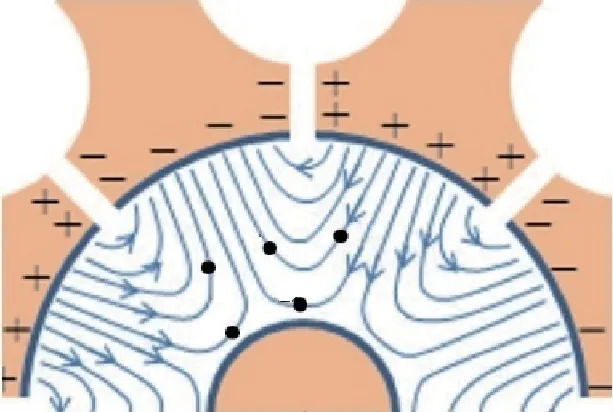
图2 阳极与阴极之间的交变电场

图3所示为某一时刻阳级和阴极之间的交变电场线(静电场电场线未画出)。A、B、C、D、E和F为该时刻6个电子的位置。所有电子距阴极的距离相同。

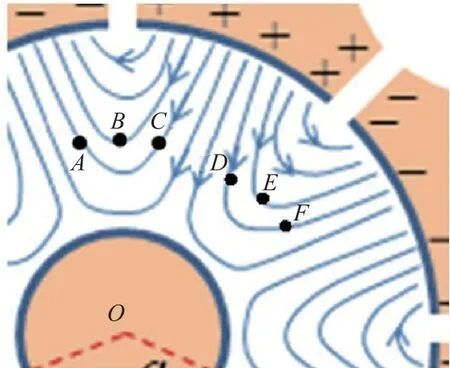
图3 另一时刻阳极与阴极间交变电场

A.5(1.2分)考虑图3中的情况,对于6个电子对AB、AC、BC、DE、DF、EF中的每个电子对,在答题纸中指出该时刻它们的漂移是否会导致它们与阴极中心O的连线的夹角增大或减小。

在问题A.5中会发现有一种聚焦机制,将阴极和阳极间的电子会聚成辐条形状。图4描绘了一个这样的辐条,用S标出。

A.6(0.8分)在答题纸中绘出此时刻的其他辐条们。用箭头们标出它们的旋转方向,并计算它们的平均角速度ωs。

假设阴极和阳极之间的中点处的总电场等于从阴极到阳极的径向静电场的平均值,并且在该中点的辐条大致是沿径向的。阴极和阳极的半径(a和b)见图4。

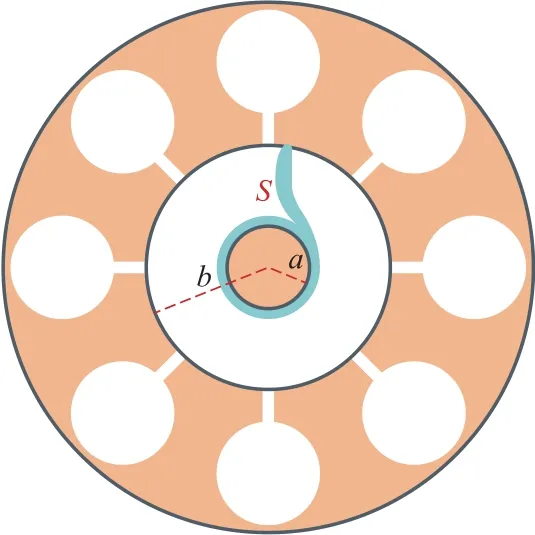
图4 阳极阴极间电子汇聚辐条示意图

A.7(1.1分)写出使磁控管以上述方式工作所需的静电压V0的近似表达式。(你计算得到的电压值是磁控管工作所需的最小值。最优工作电压会更高一些。)

PartB:微波辐射与水分子的作用(3.4分)

这部分我们利用微波辐射(从磁控管的天线辐射进微波炉的食品室)来烹饪,就是加热一种有损耗的介电材料,比如纯净水或者盐水(盐水可以看作汤的模型)。

电偶极子模型是一对大小相同的正负电荷q与-q间隔一段距离d,电偶极矩矢量从负电荷指向正电荷,大小为p=qd。

B.1(0.5分)写出下列表达式:电场作用在电偶极子上的力矩的大小τ(t),以及电场传输给电偶极子的功率的大小H i（t）。用p0,E（t）,θ（t）和它们的导数来表示。

水分子是有极性的,因此可以当成电偶极子来处理。但由于在液态水分子之间强大的氢键,我们不能将水分子视为各自独立的偶极子。因而我们应该考虑极化矢量P(t),它是偶极矩密度(单位体积的水分子的平均电偶极矩)。极化矢量P（t）平行于作用在该处的局域交变电场(由微波产生),E(t),并随时间振荡,振荡幅度正比于局部交变电场的幅度,但有相位滞后δ0。

B.2(0.5 分)写出单位体积的水吸收功率的时间平均值〈H（t）〉的表达式。含时的周期函数在一个周期内的时间平均值的定义为

现在考虑微波辐射在水中的传播。水的相对介电常数(在电磁场频率下)为εr,相应的水的折射率为,电场的瞬时能量密度为。磁场与电场的时间平均能量密度相等。

B.3(1.1分)用I（z）来表示辐射能量通量密度(energy fluxdensity)的时间平均(即单位面积上的平均辐射功率流)。这里z是进入水的深度,辐射沿z方向传播。写出该通量密度I（z）对z的依赖关系式,该通量密度在水表面的值I0可以出现在结果中。

位相差δ是由于水分子间的相互作用导致的结果。位相差取决于无量纲的介电损耗系数εl和相对介电常数εr(两个常数都与微波辐射的角频率ω和温度有关),且具有以下关系:tanδ=εl/εr。当δ足够小时,在水中深度为z处的电场为

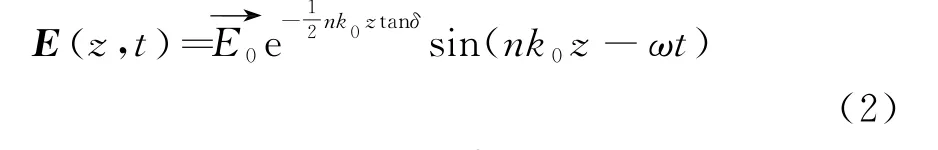
其中k0=ω/c,c=3.0×108m/s是真空光速。

B.4(0.6分)在tanδ≈sinδ近似关系下,利用其他参数写出B.2问中系数β的表达式。

图5画出了纯水(实线)和稀盐水(虚线)的εl(深色)与εr(浅色),在几个不同的温度下,随波长或频率的变化。箭头指示了从0～100℃的各曲线.角频率ω在图中用一条粗的竖直线标出,下面我们只考虑微波辐射在此频率时的情形。

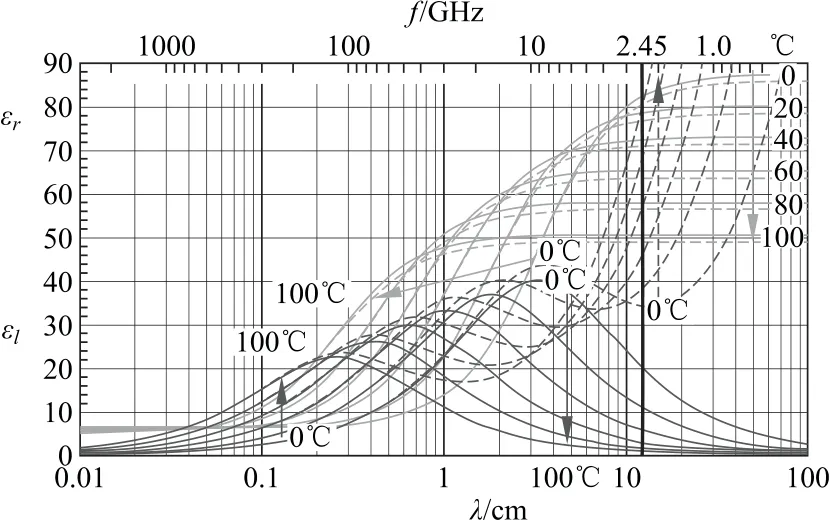
图5 纯水(实线)和稀盐水(虚线)的εl(深色)和εr(浅色),在不同温度随波长的变化

B.5(0.7分)利用图5回答下列问题:

1.对于20℃的纯水,计算出进入深度z1/2的值,z1/2是指在这一深度时单位体积的功率是z=0表面处的一半。

2.在答题纸中指明微波照射纯水时,随温度升高,进入深度是增加,减少还是保持不变。

3.在答题纸中指明微波照射汤(稀盐水)时,随温度升高,进入深度是增加,减少还是保持不变。

2 题目解答与点评

磁控管的处理,若用电动力学中给定阴极阳极电压V,和沿着管轴向垂直于纸面(图1)的磁场B,以及磁控管的形状(边界条件),理论上是可以计算电磁场分布以及电子在其中的运动,但非常复杂,这不是本题的目的。题目的巧妙之处,是将复杂的理论计算进行了模型简化,使得物理图像更清晰。所以这里先谈谈这个物理图像。

如图6(a)所示,阴极(中间铜轴)和阳极(外部铜壳,但被钻有谐振腔),外加电压(阴阳极间的静电场)后电子会从阴极飘向阳极,对阳极充电。由于谐振腔带有电感L电容C,形成了LC 电路,会产生电荷分布的振荡。所以电子在阳极的分布虽然有对称,却不是均匀的。电荷会形成图6(b)中显示的各谐振腔间正负交替分布,并产生交变电场。在外加垂直磁场和谐振腔产生的交变电场共同作用下,电子进而会产生如图6(b)的聚焦现象。电子流(图6(b)中的“触手”)在某一时刻如图6(b)显示那样会集中在几个方向。随着谐振腔LC振荡引起的电场交变变化,以及外加静电场的作用下,电子流会产生旋转,进而辐射出电磁波(微波)。这部分在题目的导言中有论述,这里结合图6希望做出更清晰的解释,对于解题和理解答案有所帮助。

2.1 LC电路计算

A.1问:如图1(b)所示的LC电路,它的谐振频率为

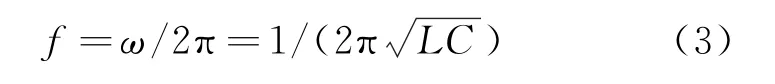
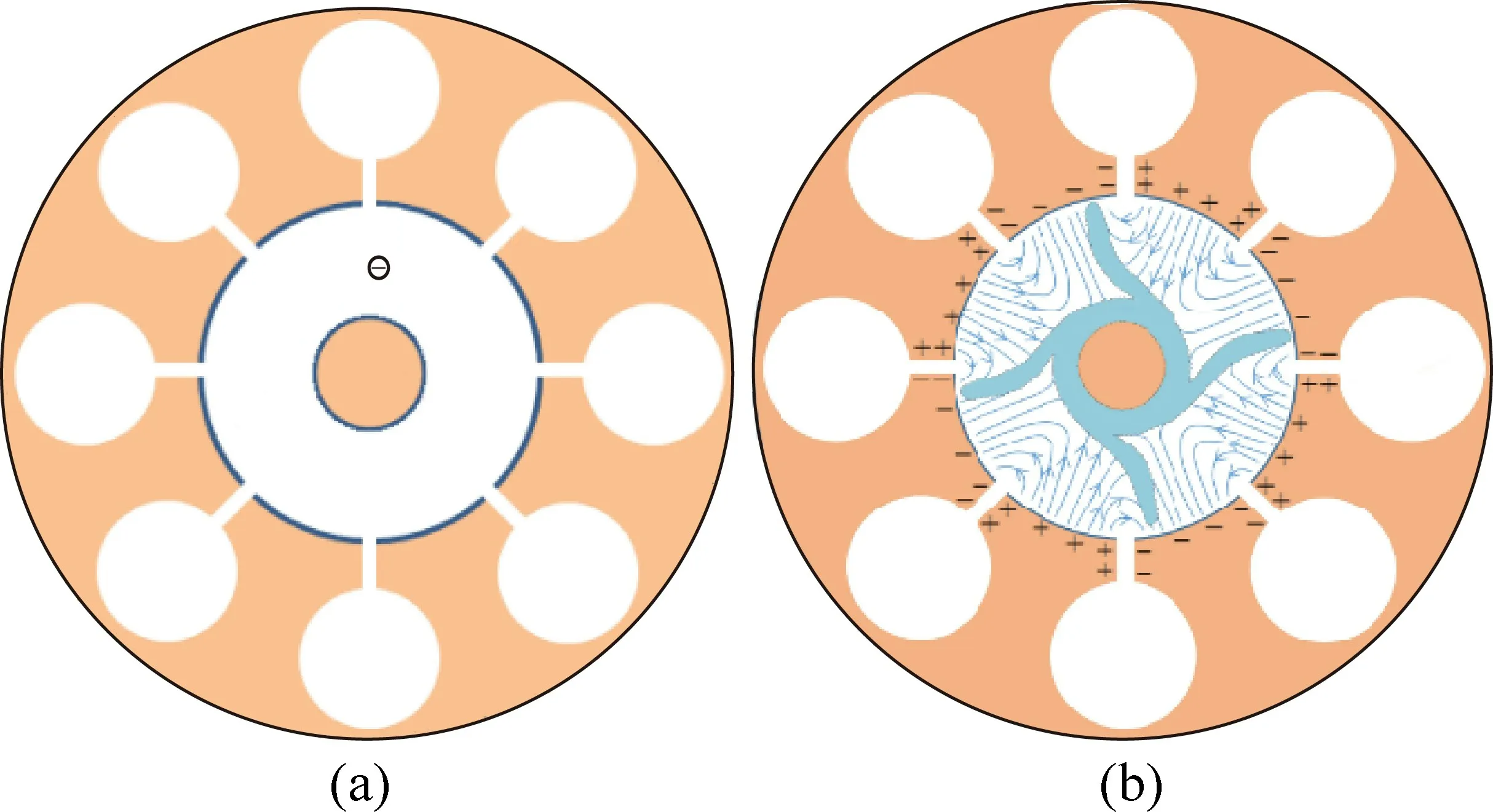
图6 磁控管阳极阴极间电场与电子的分布示意

L、C分别为谐振腔的电感与电容,所以要计算L、C。题目中描述了电容主要来自谐振器表面的平面部分,而电感来自圆柱形部分,图1b给出了尺寸数据。电容相当于:长h=17.5mm,宽l=6mm,间距d=1mm 的平板电容(用无限平板近似),其电容值C

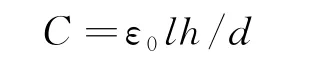
圆柱电感依题意相当于半径为R=6mm 螺线管,但电流等效为0.6I。磁场强度B

I为环绕腔体的总电流,I/h相当于螺线管电流线密度。磁通量:πR2B,则电感L

带入谐振频率式(3)以及l,h,d,R数值,可知估算的频率f est

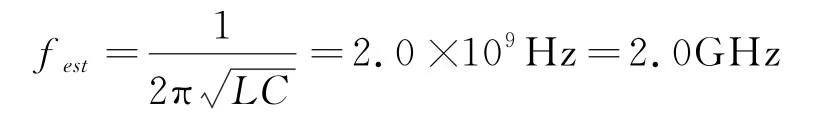
如题所述,这一估算频率与实际频率f=2.45GHz有所不同,后面计算中使用的是实际频率。本问考查了电磁学中电容,电感和LC 电路的基本知识。

2.2 电子在电场磁场中的运动

综上,可以画出两种不同初始速度下运动的轨迹(深色,浅色分别代表初始条件1,2)如图7所示:

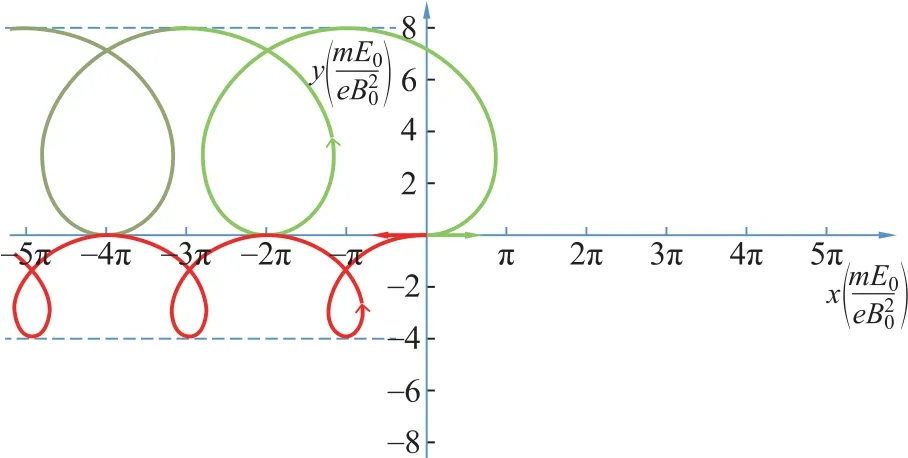
图7 不同初始速度下电子回旋运动的轨迹

从计算结果可知:相比于磁控管阴极阳极之间的距离(15mm),回旋半径很小;因而在后面的问题中我们可以忽略电子的回旋运动而只关注漂移运动。这大大简化了下面对于电子聚焦的处理。

2.3 电子束的聚焦与旋转

A.4问:如上文中我们发现电子在磁控管阴极阳极间的运动可以近似当作纯的漂移运动而忽略其回旋。而在A.2 问的分析中我们又知道:;方向与E×B同向。本问中关心的是电子速度的径向分量,磁场B垂直之面朝外,因此只有电场E的切向分量影响电子径向速度。静电场部分没有切向分量,所以我们只需考虑交变电场部分。如果它的切向分量顺时针,电子漂移速度将指向阴极;若电场切向分量逆时针,电子将飘向阳极;若无电场切向分量,则电子运动完全垂直径向。

从图8中可看出,A,B点处的电子将飘向阴极;而C,D,E处的电子飘向阳极。本问完全不需要计算,但是考查上面分析中的物理图像。

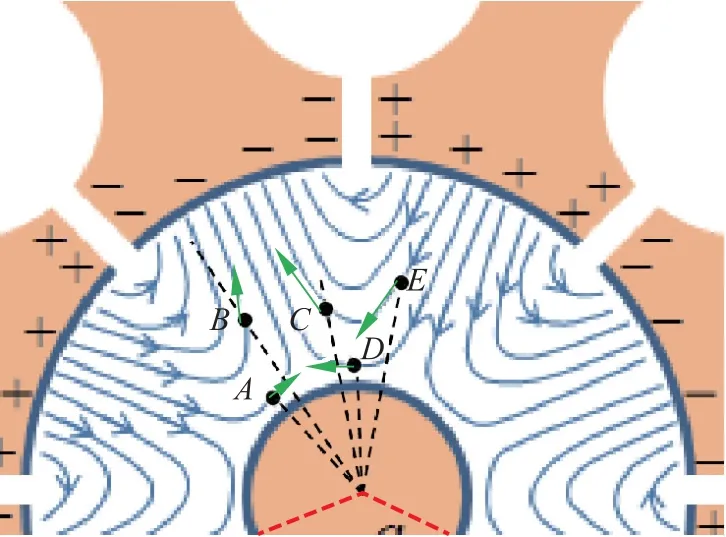
图8 A、B 处的浅色线标出交变电场此时的方向

A.5问:本问是要考虑图3中各电子漂移速度的切向分量,进而判段题目中的电子对是否汇聚(相对中心夹角减少)或发散(夹角增大)。而速度的切向分量,则取决于图3中各位置电场的径向分量。又因为图中各点到中心的距离一样,所受径向静电场相同(指向中心的静电场会使各电子具有逆时针的漂移速度分量,但这一速度对所有同一半径上的电子都一样),所以电子的汇聚与发散将只取决于交变电场的径向分量。

参见图3,若交变电场的径向分量是指向中心,会使那里的电子漂移速度有逆时针分量,如C,D处;若径向分量指离中心,会使那里的电子漂移速度有顺时针分量,如A,F处;在B,E处的交变电场径向分量近似为0,那里电子没有额外的切向速度分量。

从上面的分析中不难看出题目所问的答案:

AB、BC、AC电子对之间角度会减少,这里电子被汇聚(聚焦)。

DE,EF,DF电子对之间角度会增大,电子发散。

A.6问:图4只是画出了聚焦的电子辐条的一部分(A.5问的ABC区间);从腔的对称设计来看,电子会在相邻的两个腔之间的区域交替汇聚,发散;所以如图9所示,共有4个汇聚的辐条。在静电场驱动下,整体逆时针旋转。

LC的振荡使得相邻腔之间正负电荷交替变化,如图9中时刻,如果经过1/2的LC周期,正负电荷分布(参见图3或图6(b))正好对调;汇聚辐条的辐条会移到初始时刻发散的地方(旋转π/4);或者经过一个LC 周期T,辐条会旋转到原来相邻辐条的位置,即旋转π/2。

图9 电子汇聚辐条示意图

已知LC 振荡频率f=2.45GHz,则辐条旋转的角频率(角速度)

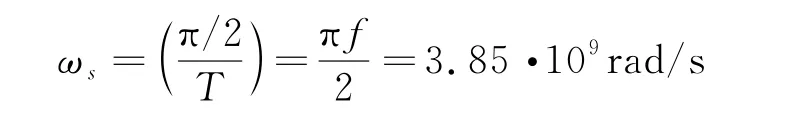
A.7问:要使得磁控管以这样的方式工作,就要让汇聚的辐条以A.6问中的角速度旋转。这样恰好同LC的振荡匹配,形成共振。这个整体旋转的速度如前所述,将取决于阴极阳极间的静电场大小。通过外加电压V0,使得电子的切向漂移速度正好与A.6中电子辐条旋转相匹配,这是最佳的共振条件。这里近似用线性处理,考虑从阴极到阳极的一半距离:r=(a+b)/2处。给定电压V0,这里的电场为:E=V0/(b-a);此处电场与恒定磁场B0引起的漂移速度为:u D=E/B0=V0/[（b-a）B0]。角速度:ω=u D/r=2V0/[B0（b2-a2）]=ωs,得到V0表达式

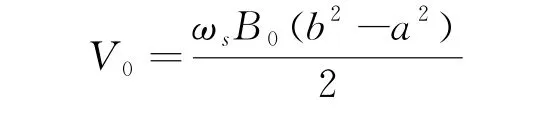
2.4 微波与水分子的作用

PartB所考查的是电磁波与物质作用的电偶极子经典模型:电偶极子在电场驱动下受迫振动,电场对电偶极子做功,因而产生电磁波的吸收。有了这样的图像,本部分几问都不算太难。

B.1问:本问就是求外加电场对电偶极子做的功。题中电场沿着x方向,电偶极子p0与之夹角为θ(t) ;电偶极子在电场力矩下做摆动式振动):电场作用在它上面的力矩为

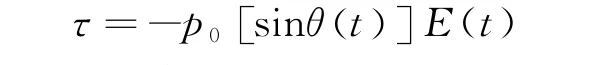
功率是力矩乘以角速度

p x（t）是偶极子的x分量。

B.2问:对式(6) (偶极子变为极化率) 做时间平均,用题目给出的电场与偶极子的表达式。注意到此时的偶极子沿电场方向(即x方向),因此P x（t）=βε0E0sin(ωt-δ)

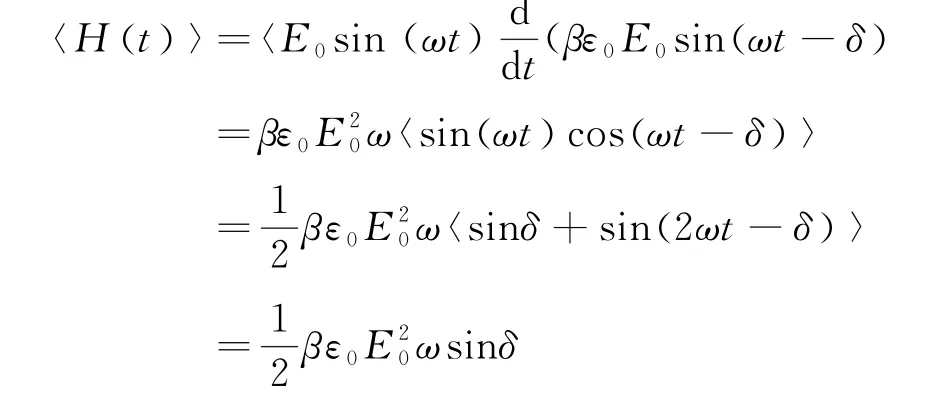
B.3问:电磁学中能流密度(也有叫光强)I是Poynting矢量的时间平均,本题可以通过Poynting矢量写出[5]。题目中给出电场能量密度,并告知磁场能相同;所以题目本意应是让学生用能流密度定义,即能量密度乘以传播速度来求解:

电磁场能量密度为

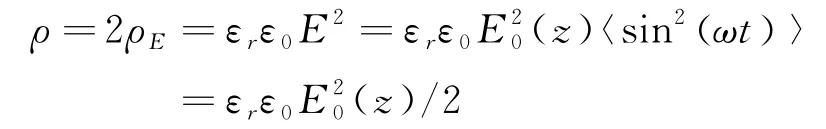
在介质中传播速度为:c/n;则能流密度

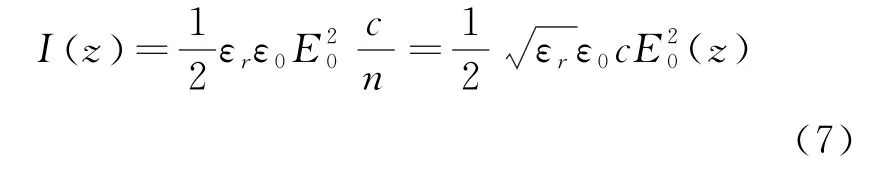
由于有吸收,电磁场在水中传播会减小,单位时间单位面积的能流在传播dz后

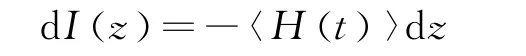
代入B.2问中的结果和关系式(7)

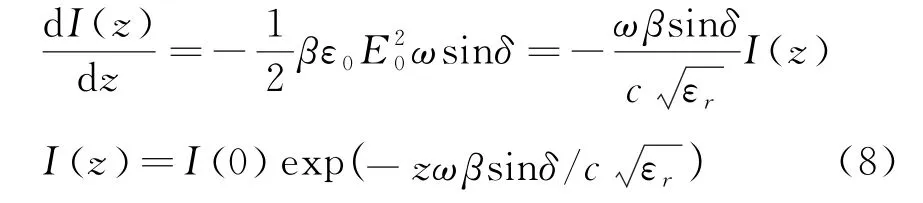
B.4问:通过式(7)与式(8),由题目中给出的电场可直接将β表达出来

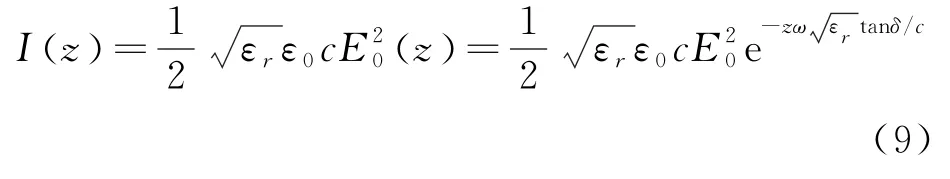
B.5问:

1) 从式(9)可求z1/2,需要从图5中读出纯水在20℃时,在给定频率ω处的εr和εl(εl是问了计算tanδ)值:εr～78;εl～10。

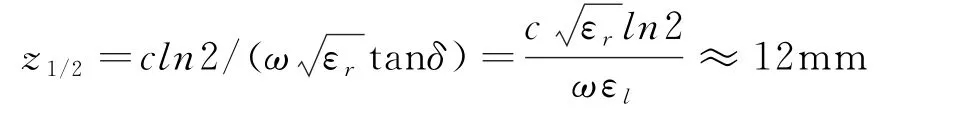
2) 进入深度z1/2在给定频率时正比于εl;从图5中容易看出,随着温度上升,在给定频率ω处的浅色的曲线(εr)下降了几倍;而深色线(εl）下降了几十倍,因而进入深度会增大。

3) 盐水的趋势(图5中的虚线)则不一样了,随着温度上升,深色虚线(εl）上升,而浅色曲线(εr)下降;所以对于盐水,升高温度减少了z1/2。换言之盐水吸收微波更有效。

3 结语

把微波炉中的核心磁控管不用复杂的电动力学计算,而是抓住其中的物理本质:LC 振荡以及电磁场对电子的聚焦是本题最精彩的地方。读懂了这个物理本质,在题目一步一步的引导下,一个简明的电子在磁控管阴阳极之间的运动图像层层展现在面前。题目的计算并不复杂,但考查了电磁学中LC振荡、电子漂移等重要且典型的问题。题目中(A.4～A.6)几问,若了解其中的物理图像,根本不用计算;但若图像不清楚,则会觉得无从下手。本题巧妙精彩的地方是,既有对物理计算的考查,同时更突出对物理图像的把握。笔者认为这让本题成为这几年奥赛中最经典的题目之一。

本题目不仅物理图像巧妙,还有贴近生活的应用。了解了题目的读者,也许大家以后再用微波炉加热食物和水时,就会联想到这里面的物理原理岂不妙哉!