某型榴弹射弹散布随阵地高程变化规律研究

蒋 明，张志远,冯 勇,王 晶

(陆军炮兵防空兵学院,合肥 230031)

0 引言

射弹散布是武器系统的重要性能指标之一，是衡量射击和命中率的重要依据。射弹散布是实弹射击时客观存在的现象，是有规律可循的，研究射弹散布，以便采取适当的措施，缩小射弹散布，提高射击效果[1]。因此，分析研究射弹散布的规律，对战斗前的弹药准备、射击方法和火力运用等都有重要影响。长期以来，火炮在高海拔地区使用问题较为突出，其根本原因是高海拔地区地理气象环境与低海拔地区存在较大差异，导致弹丸在高海拔地区的气动特性、弹道特性、射弹散布特性等发生了显著变化[2]。在高海拔地区，气象条件统计特性和低海拔地区相比，有较大的变化，这必然会对弹丸飞行弹道产生很大影响，除此之外，在高海拔地区，相同的射角条件下，随着阵地高程的增加，弹丸飞行弹道所经历的空气层也发生了改变[3]。常规火炮弹丸在平原地区的弹道主要集中在对流层内，而在海拔3 000 m以上地区，由于阵地高程增加，弹丸飞行弹道会提高至对流层中上部和平流层，弹道所经历的大气环境发生了变化，进而影响其弹道特性[4]，使得射弹散布特性发生变化。关于这一特定条件下气动特性变化[5]、弹道特性的变化[6]，已有较多单位展开了相关研究，但在射弹散布方面关注较多的为纵向密集度的研究[7]，以及通过小样本的实弹射击试验获取某一种弹丸的射弹散布特性，直接利用高海拔地区气象统计特性(平均气象模型)和刚体弹道模型，通过大样本的射击试验模拟仿真研究射弹散布特性的文献不是太多。

文中以某大口径榴弹六自由度外弹道模型和高海拔地区平均气象模型为基础，选取主要随机干扰因素，根据蒙特卡洛法，对旋转稳定弹丸在不同阵地高程的射弹散布进行分析，进而得到在高海拔地区某弹丸的纵向密集度和横向密集度等射弹散布参数总体变化趋势，研究结果对高海拔地区实弹射击选用射击方法和火力运用具有一定参考意义。

1 某大口径榴弹刚体弹道模型与气象模型

无控旋转弹丸的运动可分为质心运动和绕心运动。根据经典外弹道理论，某大口径榴弹的6自由度刚体弹道方程组[8-9]为：

(1)

式中:Fx2,Fy2,Fz2分别为弹丸受到的力;Mξ,Mη,Mζ分别为弹丸受到的力矩;m为弹丸质量;v为弹丸速度;A和C为弹丸转动惯量;θa和ψ2为弹道倾角和速度偏角;φa和φ2为弹轴纵向姿态角和横向姿态角;ωη,ωξ,ωζ为弹轴摆动角速度;x,y,z为弹丸质心坐标;t为时间自变量。

以上方程联立起来即是无控旋转弹丸的六自由度刚体弹道模型，式中各参数详见文献[8]。当已知弹丸结构和气动参数、起始条件、气象条件、射击条件，即可积分求解弹道。其计算精度取决于各个参数的准确程度。

在高海拔条件下解算上述模型时，为了使得解算结果具有一般性分析意义，还需明确气象条件的标准值。现行的炮兵标准气象条件主要是根据低海拔地区的气象统计数据得出的，与高海拔地区气象条件统计数据的数值特征存在较大偏差，已有相关文献研究了高海拔地区的平均(标准)气象条件问题,并指出若以炮兵标准气象条件进行弹道解算，高海拔地区的平均气象条件与现行的炮兵标准气象条件之间的差异性将会带来较大的解算偏差[10]。

为了使得研究更贴近实际情况，文中选取的气象模型为文献[10]给出的高海拔地区(起点为海拔1 000 m)气象模型，具体模型为：

1)以海拔1 000 m为地面起算，其地面标准值为：虚温τ0n=296.65 K，气压p0n=1.013×105Pa，空气密度ρ=1.0494 kg/m3，无风。

2)海拔1 000 m以上，虚温随高度的分布为：

(2)

式中，各参数取值如表1所示。

3)气压标准定律根据“大气铅直平衡假设”可以得到：

(3)

式中：g为重力加速度，取值9.8 m/s2;R为气体常数，取值287 J/(mol·K)。

2 利用蒙特卡洛法的射弹散布仿真

火炮射击过程中，射弹散布会受到诸多因素的影响。根据外弹道理论，影响射弹散布的主要因素有初速散布、跳角散布、阻力系数散布和气象诸元散布等。高海拔条件下，由于环境条件的变化，弹丸初速、空气密度、起始扰动、跳角散布等都会随阵地高程变化而变化，它们对射弹散布的影响各不相同，如果分别研究各因素对射弹散布的影响，不仅十分复杂，而且射弹散布误差对每发弹丸的影响是随机的，难以准确分析。

为此，将众多的随机干扰因素简化归结为初始扰动角度、初始扰动角速度、随机风等三大方面的随机干扰。在相同的初始射击条件和随机干扰条件下，间隔1 000 m选取阵地高程，采用蒙特卡洛法模拟射击试验[11]，并统计弹丸密集度，根据统计结果分析射弹散布随阵地高程的变化规律。

射弹散布与弹丸受到的随机干扰密切相关，由于随机干扰导致的误差大部分服从于正态分布定量[12]，可认为由这些随机干扰产生的射弹散布也服从正态分布定量，即射弹散布服从正态分布定律。射弹散布包含距离散布、方向散布和高低散布，为了使研究具有一般性，假定目标在炮口水平面，此时，高低散布体现在距离散布和方向散布中，只需要分析距离散布和方向散布随阵地高程的变化规律即可。

利用蒙特卡洛法进行射弹散布仿真的基本思想是模拟射击，利用计算机生成弹道的随机干扰因素，从而模拟落点，然后通过大量仿真计算，根据落点位置分析随机干扰作用下落点的统计特性，利用该统计特性模拟某大口径榴弹射弹散布的情况。

仿真时，不同高程时的扰动因素取值不变，弹丸的初始扰动角度、初始扰动角速度、随机风等主要扰动因素具体取值如表2所示。

表2 主要扰动因素及量值

3 射弹散布随阵地高程变化仿真分析

根据外弹道学理论和某155 mm榴弹在低海拔时的实弹射击结果，表征其射弹散布的公算偏差数值在全号装药时对应的最大射程处达到最大值，因此在仿真计算时，初始条件为：装药号选取全号装药，初速为930 m/s，射角为45°，气象条件采用海拔1 000 m以上地区平均气象模型，主要扰动因素及量值采用表2中的数据。根据蒙特卡洛法在海拔1 000 m,2 000 m,3 000 m,4 000 m和5 000 m等不同高程条件下分别对射弹进行300次射弹散布的仿真。为了便于全面比较随着阵地海拔增加时射弹散布的变化情况，对该弹在阵地海拔0 m、现行炮兵标准气象条件情况下的射弹散布一并进行了仿真计算。

射弹散布仿真的结果如图1～图6所示。图中，横轴沿射击方向，纵轴沿垂直射击方向。

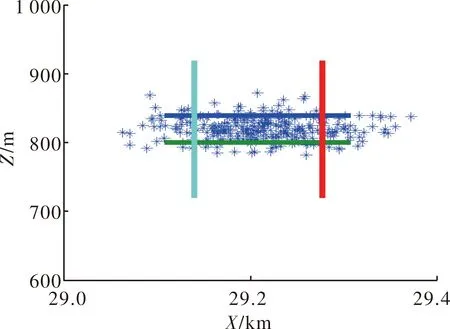
图1 高程0 m射弹散布

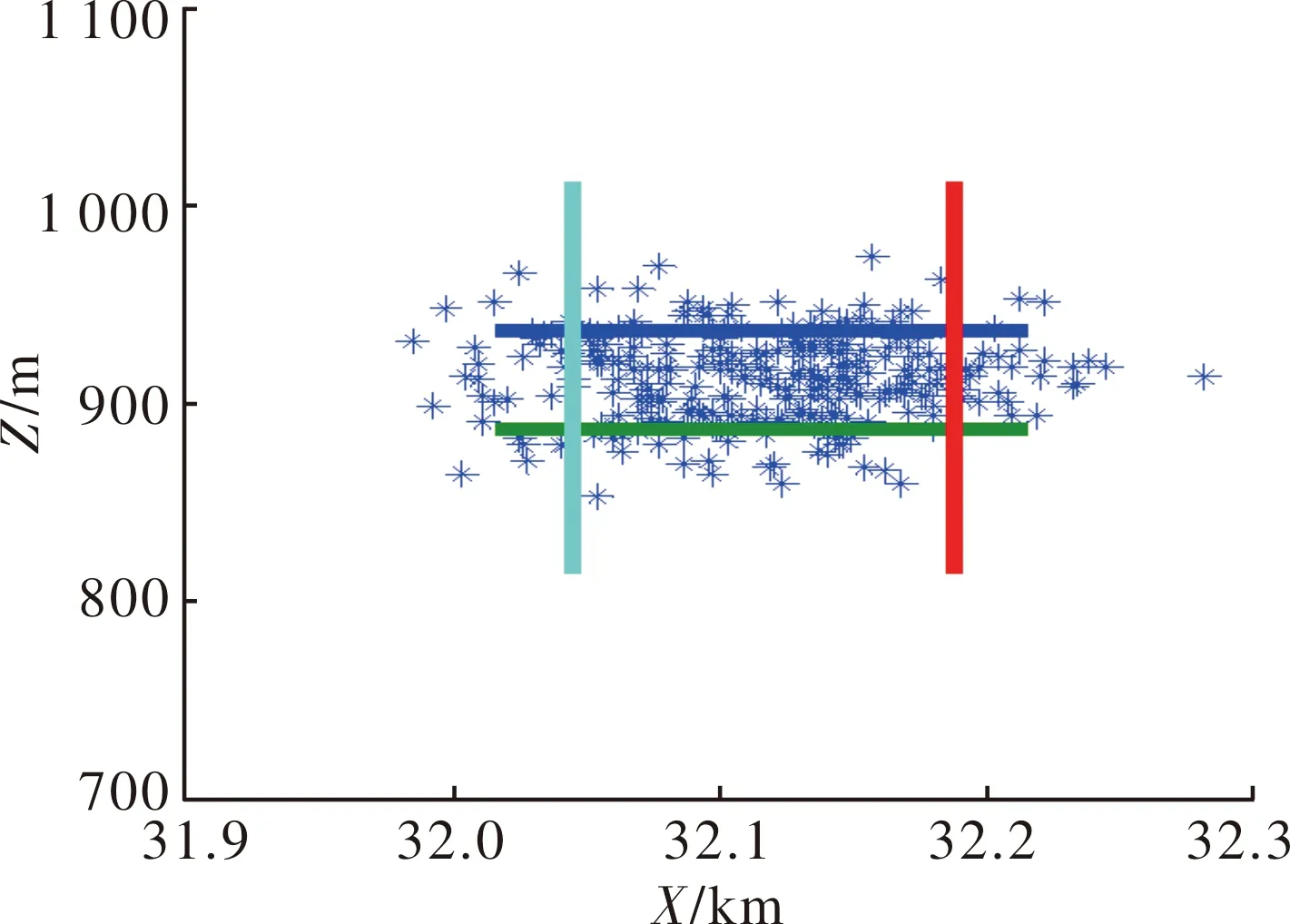
图2 高程1 000 m射弹散布

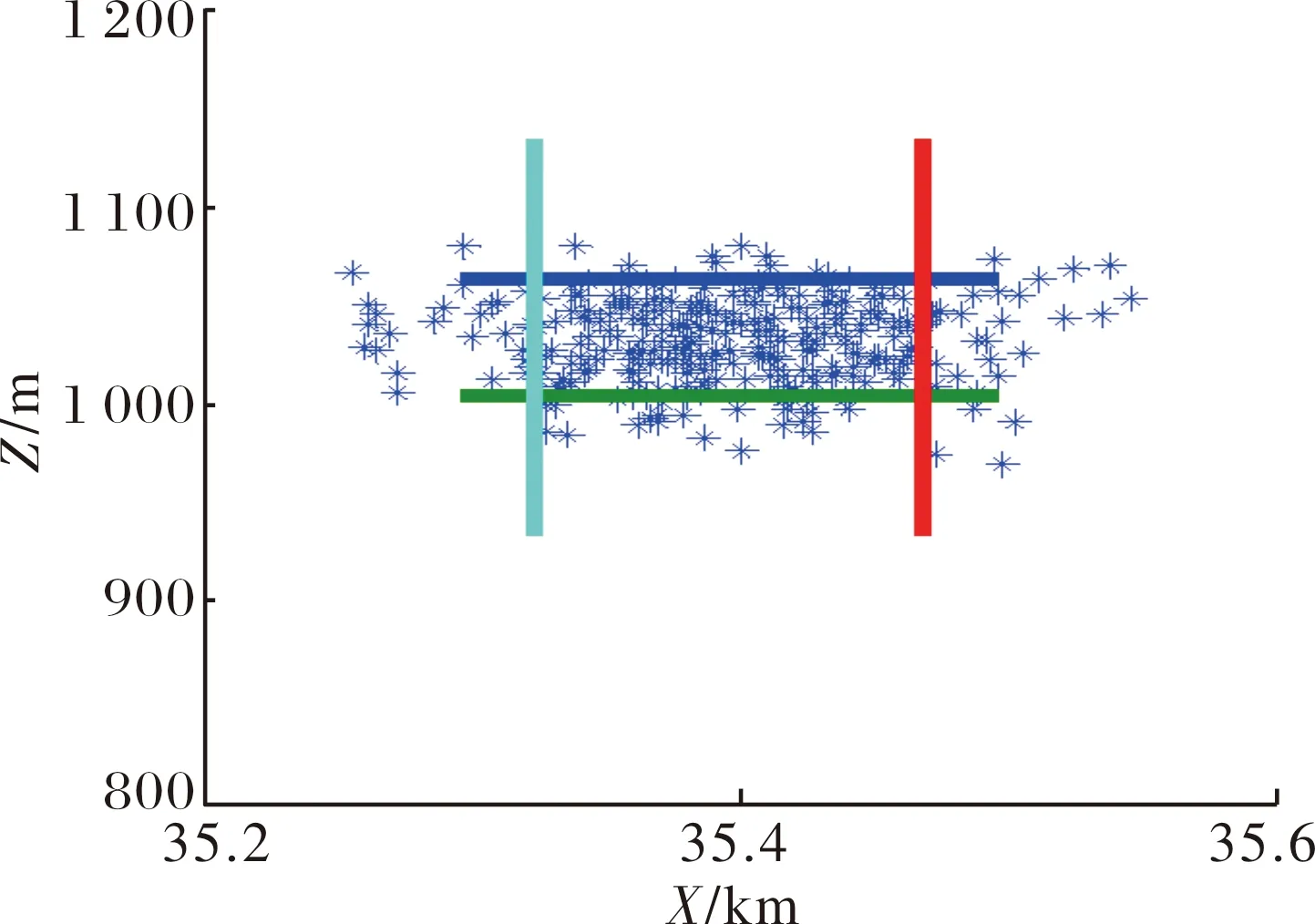
图3 高程2 000 m射弹散布

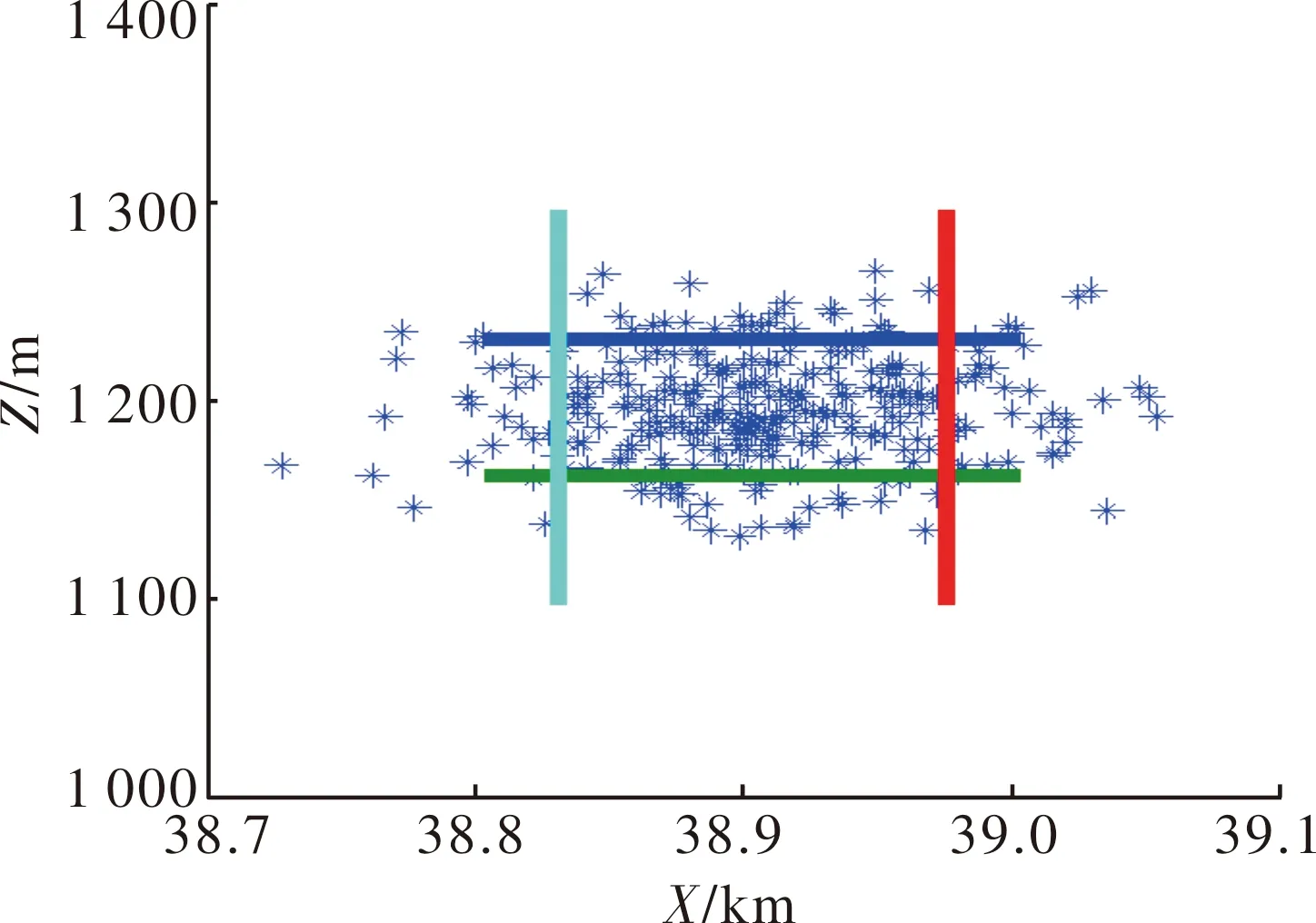
图4 高程3 000 m射弹散布

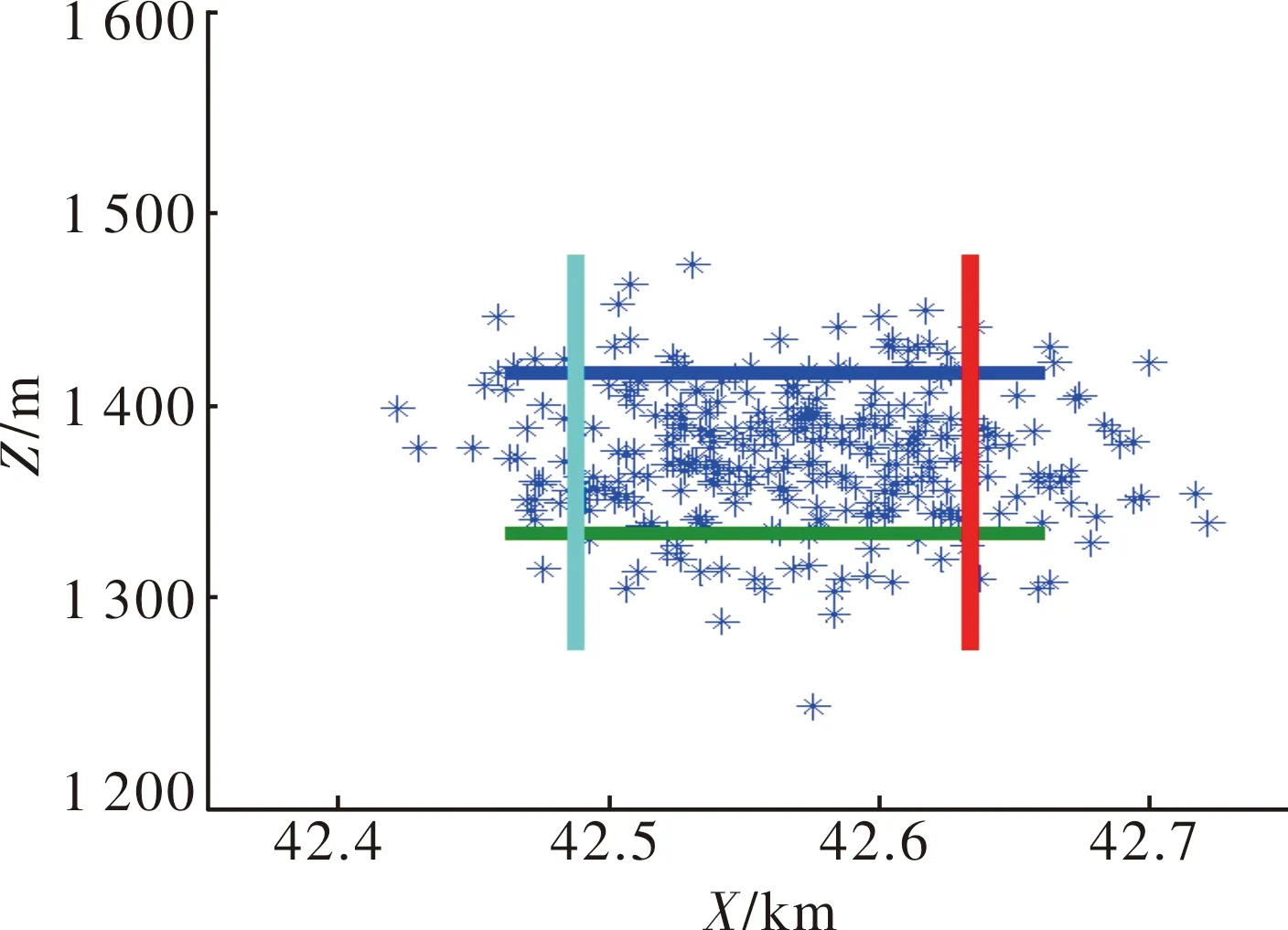
图5 高程4 000 m射弹散布

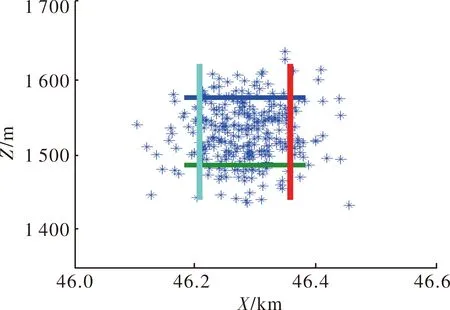
图6 高程5 000 m射弹散布

从射弹散布的仿真结果可以看出，在45°射角情况下，随着阵地高程的增加，弹丸落点的分布发生了变化，散布幅员形状由沿射击方向的长扁形逐渐变为宽扁形，也就是距离散布与方向散布比值减小。散布幅员形状由沿射击方向的长扁形逐渐变为宽扁形，这对不同高程条件下优化选择打击不同幅员的目标具有一定的参考意义。射弹散布随高程变化数据情况见表3。

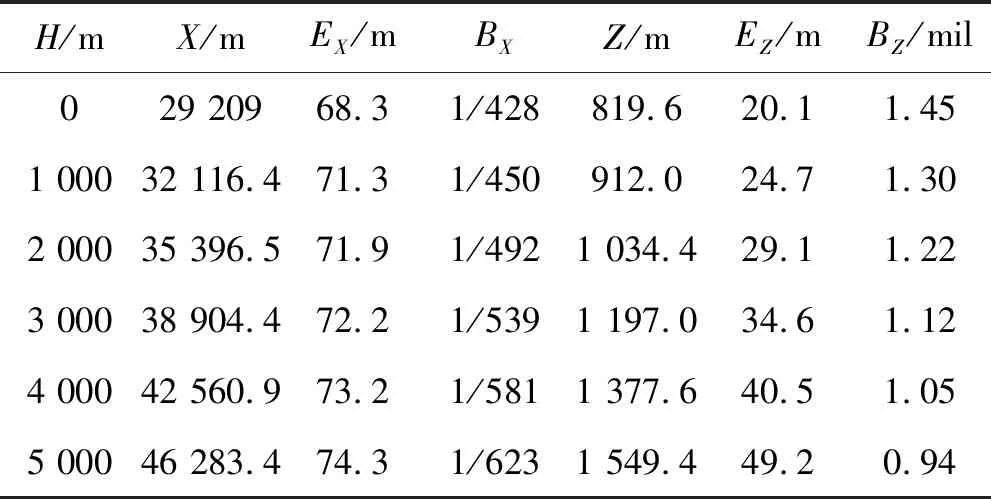
表3 射弹散布随高程变化

表中:H为阵地高程；X为落点的散布中心对应的射程;EX为距离散布的中间误差；BX为纵向密集度的离散系数(也称变异系数)，即BX=EX/X，该值为无量纲参数；Z为落点的散布中心对应的横偏；EZ为方向散布的中间误差；BZ为横向密集度离散系数，即比值EZ/X，通常换算成角度，以mil表示该参数的量纲。EX和EZ表征了射弹散布的幅员特征，BX和BZ表征射弹散布的密集度特征。

通过表3数据可以看出，随着高程的增加，射程密集度离散系数和方向密集度离散系数都随高程的增加而减小。高程5 000 m时，射程密集度离散系数比海拔0 m减小了32%，而方向密集度离散系数减小了35%。也就是说高海拔条件下，旋转稳定弹丸的密集度增强，射弹散布变小。从表中数据也可以看出，随着高程的增加，相同射角条件下的射弹散布幅员是逐渐变大的，这似乎与刚才的结论不一致，但若在相同射距上考察射弹散布，随着高程的增加，射角必然减小，从而散布幅员必然减小，即射弹散布随着高程减小。因而，总体而言高海拔地区射弹散布性能优于低海拔地区下射弹散布。该型榴弹的射弹散布之所以会随阵地高程变化呈现上述规律，主要是由于旋转稳定弹丸的陀螺稳定性和动态稳定性随阵地高程的增加而增强[11]，因此在相同量值的随机干扰因素的作用下，阵地海拔增加时，随机干扰对弹丸飞行弹道的影响作用和对弹丸落点的影响程度必然降低。

4 结束语

根据6D弹道模型，以某型榴弹为例，采用蒙特卡洛法对全号装药下45°射角、不同阵地高程时射弹散布的变化规律进行了仿真分析。根据仿真计算结果，在高海拔条件下随着高程的增加，射程密集度和方向密集度逐渐减小。散布幅员形状由沿射击方向的长扁形逐渐变为宽扁形，这对优化选择打击目标具有一定的参考意义。