基于非线性规划的中近距空空导弹增程弹道设计方法
2021-03-18王龙,李斌
王 龙,李 斌
(中国空空导弹研究院,河南洛阳 471000)
0 引言
在实际空战条件下,“先敌发现、先敌发射、先敌命中、先敌脱离”是飞行员能够制胜的“四先”准则,追求射程的不断提高是空空导弹不变的发展方向之一[1-2]。在导弹发动机推力和阻力特性确定的条件下,导弹的最大发射距离取决于实际的飞行弹道。因此,增程弹道设计是能够让飞行员实现“先敌发射”的一项关键技术。在工程应用中,传统的空空导弹增程弹道设计方法是先确定一种弹道方案,然后基于仿真数据对弹道方案中的相关参数进行调试和设计[3]。该方法在一些弹道条件下能获得较好的性能,但由于空战环境复杂多样,通过离线仿真设计的参数难以适应所有弹道条件。为了避免导弹攻击区出现漏洞,通常需要进行大量的仿真并对参数进行反复修正,效率较低。
弹道设计本质上属于非线性优化问题,针对该类问题目前常用的理论方法有间接法和直接法。间接法是将优化问题转化为两点边值问题进行求解,对初值精度要求高,选取不当可能无法得到计算结果,且求解过程比较复杂,因此在复杂弹道设计问题上的应用颇受局限[4]。直接法是将连续的优化问题进行参数转化,然后再通过合适的方法进行求解。常用的直接法主要有直接打靶法[5]、多重打靶法[6]、配点法[7]、微分包含法[8]等。目前配点法中的伪谱法已成为轨迹优化问题的主流方法。该方法的特点是在时间节点上通过插值多项式对控制变量和状态变量进行近似,并将微分方程约束转化为代数约束,然后通过常规的方法进行求解[9]。伪谱法的最大优点是对初值不敏感、收敛较快且计算精度高,因此在航天飞行器的轨迹优化上已得到了广泛应用[10-15]。
空空导弹飞行时间短,飞行过程中推力和质量时变,升阻比系数小,大气参数依赖导弹的飞行高度,且要攻击空中运动目标,因此空空导弹的增程弹道设计是一类复杂的时变动态规划问题。鉴于伪谱法的诸多优势,文中首先基于伪谱法将空空导弹的增程弹道设计问题进行参数化描述,转化为一般的非线性规划问题进行求解,然后给出求解方法。
1 空空导弹增程弹道设计问题描述
1.1 运动模型
1.1.1 导弹运动模型
对于空空导弹,其在弹道坐标系下的三自由度运动模型为:
(1)
式中:xm、ym、zm为导弹在惯性坐标系下的坐标;vm为导弹速度大小;θm、ψm分别为导弹的弹道倾角和弹道偏角;m为导弹质量;ms为发动机的燃烧速率;P为导弹发动机推力;X、Y、Z分别为气动阻力、升力和侧向力;α、β分别为导弹的攻角和侧滑角。
1.1.2 目标运动模型
目标运动模型为:
(2)
式中:xT、yT、zT为目标在惯性坐标系下的坐标;vT为目标速度大小;θT、ψT分别为目标的速度俯仰角和方位角;nθT和nψT分别为目标的俯仰机动过载和方位机动过载;nT为目标机动过载大小。
1.2 空空导弹增程弹道设计问题描述
1.2.1 约束条件
空空导弹在飞行过程中受到的约束主要有推力约束、质量约束、控制输入约束以及终端约束等。
1)推力约束
中近距空空导弹的发动机通常为一级,推力的约束形式为:
(3)
式中:P0为导弹发动机推力大小;t1为导弹发动机的工作时间。
2)质量约束
在主动段,导弹的质量随着发动机燃料的燃烧减小;在被动段,导弹的质量保持不变,因此导弹的质量约束为:
(4)
式中,ms0为发动机的秒消耗量。
3)控制输入约束
在三自由度模型中,导弹的控制输入为攻角和侧滑角,其约束条件为:
(5)
式中,αmax、βmax分别为攻角和侧滑角的最大值。
4)终端状态约束
设导弹可容许脱靶量的最大值为Rmax,则导弹的终端约束为:
(6)
1.2.2 增程弹道设计问题描述
对于空空导弹,在评估其射程指标时一般以一定速度作为截止条件。在实际作战时,空空导弹的实际射程取决于发射时刻的弹-目相对距离,设计空空导弹的拦截弹道时可以将末速大小作为指标,因此增程弹道设计问题可描述为:
(7)
其中,tf为终端时刻,动态微分方程约束为式 (1)和式(2)。
2 基于非线性规划的空空导弹增程弹道设计
下面基于伪谱法对弹道设计问题进行参数化描述,然后给出弹道设计的求解算法。
2.1 基于伪谱法的弹道设计问题参数化描述
2.1.1 微分方程的参数化
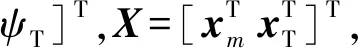

(8)
其中,u=[αβ]T。
将时间区间[t0,tf]转换到[-1,1],引入时间变量τ,其定义为:
(9)
插值时间节点是时间区间[-1,1]内的N阶Legendre多项式P(τ)的根,其中P(τ)可表示为:
(10)
通过求取[-1,1]内的N个Legendre-Gauss插值点τ1,τ2,…,τN,则系统在τ1,τ2,…,τN处状态值的Lagrange插值多项式为:
(11)
式中,Li(τ)为插值基函数,其表达式为:
(12)
同理,系统在τ1,τ2,…,τN处控制输入的Lagrange插值多项式为:
(13)
(14)
由于τ1,τ2,…,τN处的状态变量和控制输入是式(11)和式(13)的参数,因此需要将运动模型参数化,从而转化为关于τ1,τ2,…,τN处状态变量和控制输入的代数约束。
对式(11)求关于时间的导数,可得:
(15)
(16)
在τk时刻,根据式(8)、式(11)、式(15)可得:
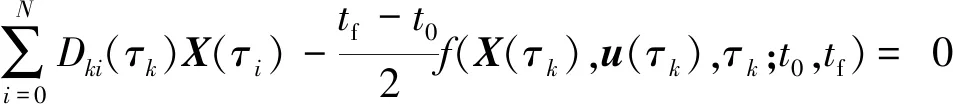
(17)
2.1.2 约束条件参数化
推力约束的参数化可描述为:
(18)
质量参数化可描述为:
(19)
输入约束的参数化可描述为:
(20)
为了描述终端约束,首先需要对终端状态进行参数化描述。根据运动模型,终端状态可描述为:
(21)
对于积分函数,可采用N个插值点的求积进行近似,即
(22)
式中wi可表示为:
(23)
于是,终端约束为:

(24)
2.1.3 指标函数参数化
指标函数的参数化描述为:
(25)
其中,vm(τf)可通过式(21)进行求解。
通过参数化描述,可将连续的无限维弹道优化问题转换为一般的非线性规划问题,即在上述参数化约束条件下,求取[t0tf]时间段内的状态变量Xk(k=1,2,…,N)、输入变量uk(k=1,2,…,N)以及终端时刻tf使得导弹终端速度最大。
2.2 弹道优化问题的求解算法
弹道设计问题通过参数描述之后转换为多约束下的非线性规划问题,下面基于序列二次规划给出求解算法。
以式(25)为优化指标,以Xk(k=1,2,…,N)、uk(k=1,2,…,N)为优化变量,以式(17)~式(19)为等式约束,以式(20)、式(24)为不等式约束的非线性规划问题可描述为:
(26)
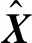
定义拉格朗日函数:
(27)
式中,λ=[λ1,λ2,…,λNeq,λNeq+1,…,λNeq+Nieq]为拉格朗日乘子系数。
下面给出非线性规划问题式(26)的求解算法。首先,求解如下的二次规划问题:
(28)
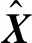
然后,通过求解如下的优化问题得到迭代步长αk:
(29)
最后,根据迭代方向dk和迭代步长αk更新状态向量:
(30)
3 仿真验证
下面通过仿真来验证文中空空导弹弹道设计方法的有效性。
3.1 仿真条件设置
假设某型空空导弹相关参数如表1所示。
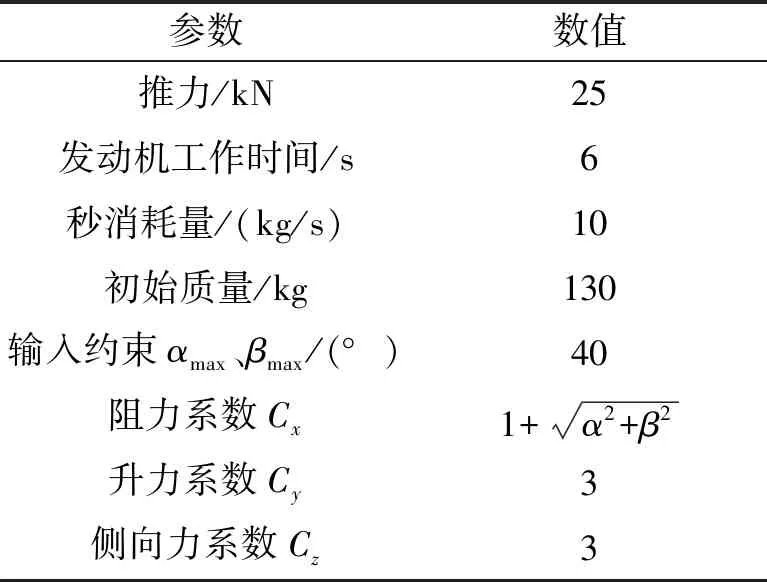
表1 某型空空导弹相关参数
假设导弹发射时刻载机和目标运动参数如表2所示。

表2 载机和目标初始运动参数
3.2 仿真结果
仿真计算得到的导弹运动状态和控制输入如图1~图4所示。图1为导弹在垂直方向上的运动轨迹,图2和图3分别为导弹的速度大小和弹道倾角曲线,图4为导弹的攻角和侧滑角输入曲线。根据图1可知,导弹的最优轨迹为高抛弹道,即爬升到高空利用空气阻力小的优势减小导弹的速度衰减率,从而达到提高末速的目的,导弹的最大高度为16 215.4 m。图2中实线为文中方法的导弹速度曲线,虚线为比例导引下的导弹速度曲线,仿真结果表明,文中方法下导弹的末速大小为323.2 m/s,比例导引下导弹的末速大小为216.3 m/s,文中方法的弹道末速比比例导引大106.9 m/s。若将323.2 m/s作为弹道仿真的截止条件,通过二分法计算得到比例导引下导弹能够命中目标的最大发射距离为30.6 km,比文中弹道设计方法的发射距离小了9.4 km,从而验证了文中弹道设计方法能够大幅提升导弹的最大发射距离。初始发射距离为30.6 km时,比例导引下的导弹速度随时间的变化曲线如图5所示。

图1 导弹和目标垂直运动轨迹
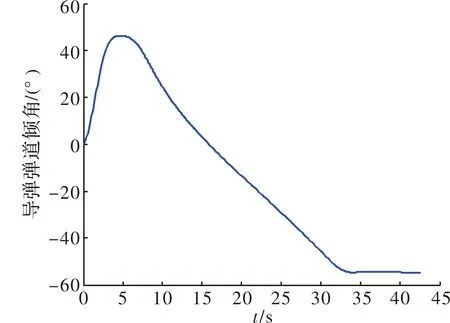
图3 导弹弹道倾角

图4 导弹控制输入
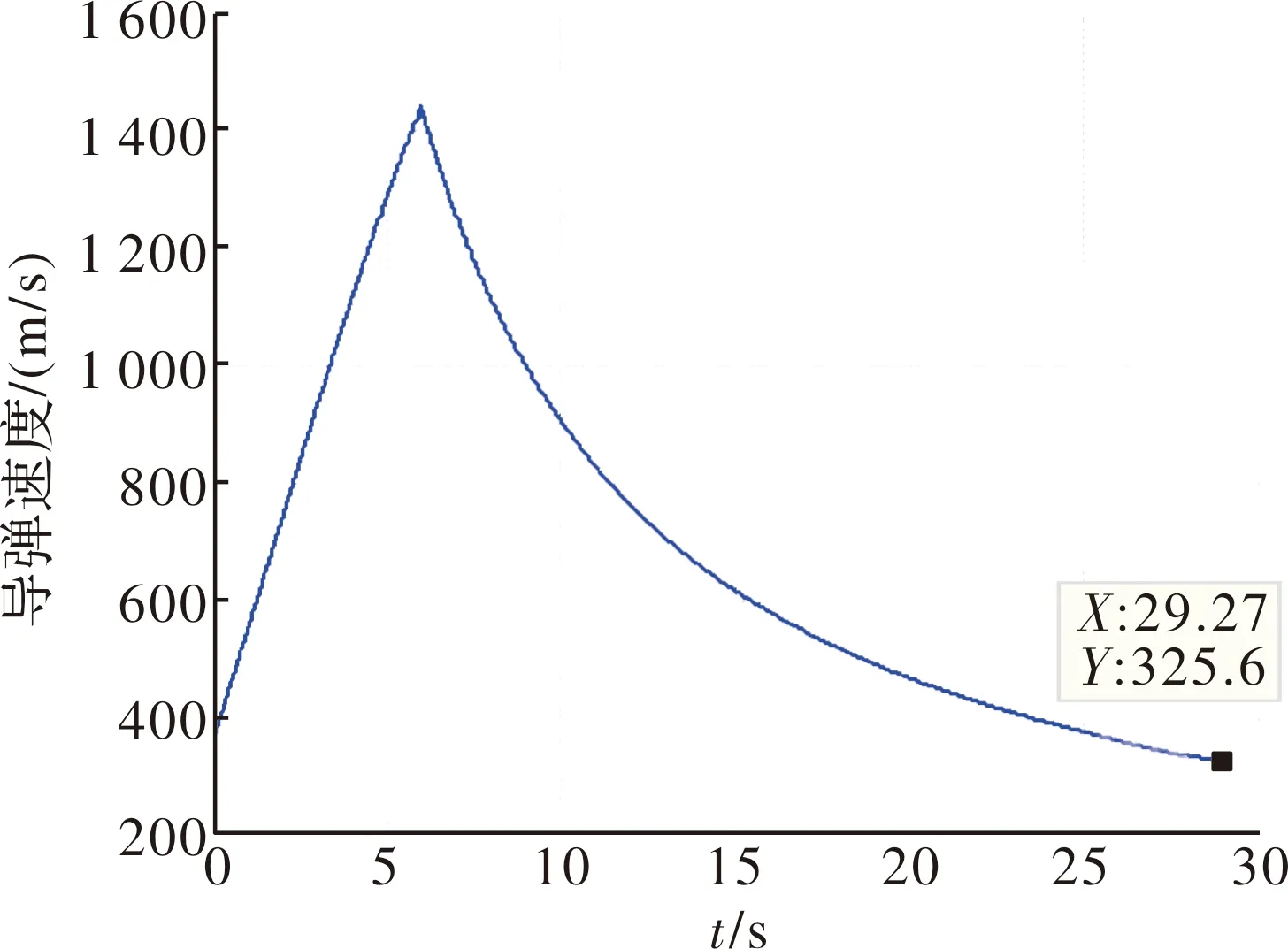
图5 比例导引下的导弹速度曲线(发射距离30.6 km)
4 结论
以近距空空导弹为对象,考虑作战过程中的实际约束条件,以导弹最大末速为指标,建立了空空导弹弹道设计问题的数学描述,基于伪谱法对弹道设计问题进行参数化描述,然后给出了求解算法,并通过数字仿真进行了验证。仿真结果表明,在给定初始发射条件下,该弹道设计方法能够显著提高导弹的末速,且计算精度较高。基于文中的弹道设计方法,在相同末速限制条件下,能够提高导弹的最大发射距离,使载机能够做到先敌发射,从而提高导弹的作战能力。
