基于方位向信息分离的机动SAR成像算法
2021-03-17马彦恒侯建强刘新海
马彦恒 侯建强 李 根 刘新海
(陆军工程大学石家庄校区 石家庄 050003)
1 引言
传统匀速直线运动状态下的SAR成像,已经不能满足侦察成像的需求。由于灵活的成像模式和广泛的应用前景,机动SAR[1–3]成像得到了越来越多的重视。复杂的运动轨迹具有更好的环境适应能力,同时也会造成更高阶的斜距方程、非均匀的空间采样和更大的方位空变性。这些变化会给回波信号的距离徙动校正、空变性校正和方位向压缩带来更大的困难。SAR成像通常有两类算法即时域算法和频域算法。其中,时域算法[4–6]运算量大,不适用于实时成像。频域算法[7–12]依托4阶斜距方程和2维频谱级数反演求解,能够较好地实现机动成像,然而并不适用于任意场景,需要针对不同的场景做不同要求的修正和改进。而利用子孔径[13]的频域算法对复杂运动轨迹进行分解,简化后进行成像,会降低方位向的分辨率。利用非均匀FFT[14]的方法只适合于解决方位向非匀速运动的问题。
本文针对机动SAR成像,提出了一种方位向信息分离的成像算法。依托空间3维坐标系,利用3维坐标在斜距方程中具有“3维同性”(即x, y, z在斜距R中意义和地位相同)的特点,通过方位向信息分离,将斜距方程中与方位向运动信息不相关的部分提取出来,用于距离走动校正和空变性校正,与方位向运动信息相关的部分用于距离弯曲校正和方位压缩。利用速度等效变换去除距离弯曲,方位压缩则可以通过非均匀傅里叶变换解决。算法将3维空间运动下的机动成像等效成方位向直线非匀速处理,不依赖于不同模型下的2维频谱计算,只与3维运动参数有关,适用性广。同时,坐标3维同性的特点,能够从不同的维度对斜距方程进行分离分析,丰富了斜距信息,实现了更多信息的提取,为后期目标识别的研究做铺垫。
2 机动SAR运动模型
SAR平台在运动过程中,主要有匀速直线运动、直线非匀速运动、俯冲、爬升、左盘转向、右盘转向等基础运动,传统的侦察模式采用的是匀速直线运动。而对于机载SAR的实战要求而言,需要在多种运动状态下都能完成侦察成像的任务。这些主要的运动模型可以用简单的3维匀加速运动表示,3维参数的不同表示不同的运动模型。本文以聚束成像模式为例进行分析,如图1所示为在空间3维加速运动模型下,机动SAR成像示意图。
平台和目标点的距离可表示为

其中,( xm,ym,zm)表 示SAR平台的初始位置,(xp,yp,0)表示成像区域内任意点目标的位置,(vx0,vy0,vz0)是SAR平台的3维初始速度,( ax,ay,az)是3维空间内的初始加速度,ta是方位向的慢时间,(xR,yR,zR)表示SAR平台在方位向ta时刻的3维空间位置,R(ta)是SAR平√台在ta时刻的斜距。式(1)还可以表示为
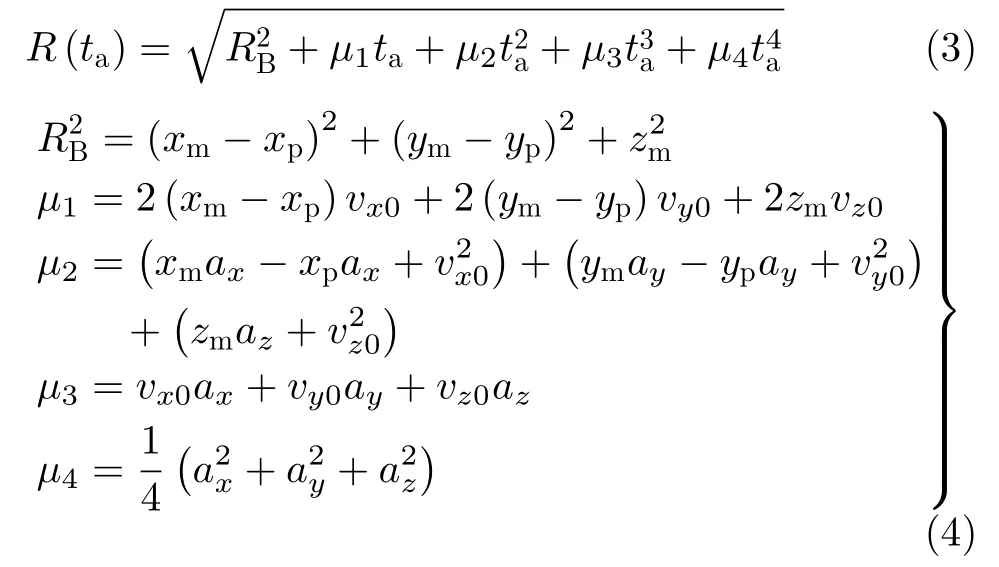
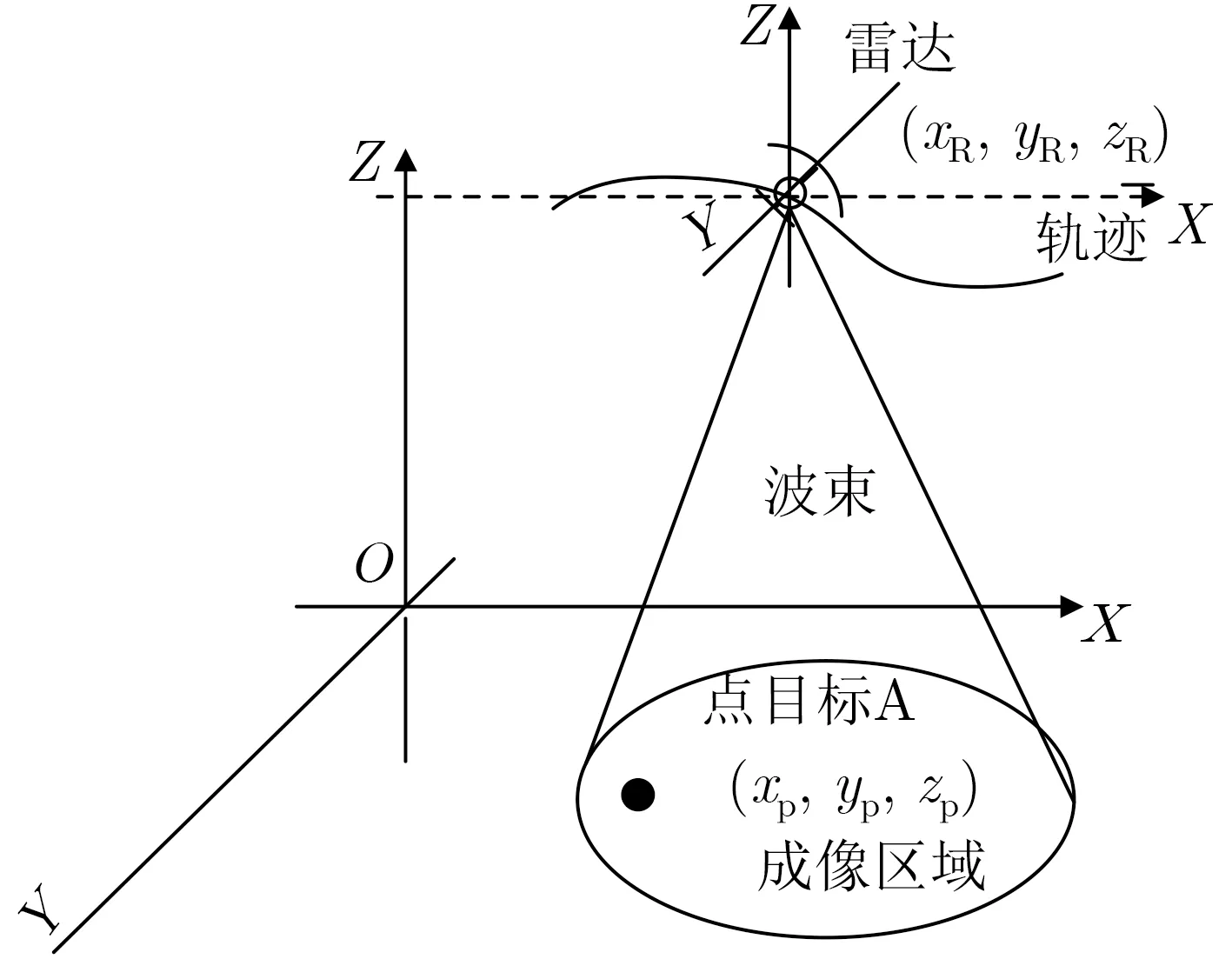
图1 机动SAR成像示意图

式(4),式(5)和式(6)比较完整地表示SAR平台在3维加速运动模型下的斜距变化情况。
3 机动SAR成像算法
3.1 斜距方程方位向信息分离
从式(1)可以看出,x, y, z在斜距R (ta)中的意义是一样的,这一现象在文中成为“3维同性”。充分利用这一点,就可以丰富成像信息。为了能够更详细地分析距离徙动、空变性变化和方位向调制的影响因素,需要将式(5)斜距方程进行方位向信息分离,其中的运动信息主要体现在系数方程组(6)中。首先,将式(6)中的分子分解成两部分:一部分分解成与目标点位置相关的,一部分分解成与目标点位置不相关的。记

当 xp=0 和yp=0时,式(6)则是与目标点位置参数无关的量,可表示为

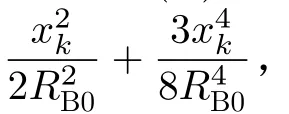
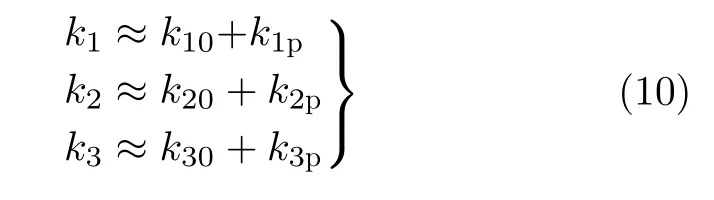




由式(7),式(9),式(11)和式(13)可得


由式(5),式(10)和式(13)可以得到斜距方程分离的结果其中,前两项表示目标点的位置,第1个“[ ]”表示距离弯曲、距离走动和非方位向的调制项,主要用于相位补偿和校正。第2个“[ ]”表示方位向的2阶和3阶调制,主要用于方位压缩。
3.2 机动SAR成像处理
3.2.1 非方位向相位补偿
忽略幅度信息,距离压缩后的回波方程可以表示为

根据式(16)中的第1个中括号的内容,构造距离频域的相位补偿函数为

将式(16)与式(17)相乘,就可以实现非方位向相位补偿,得到结果如式(18)
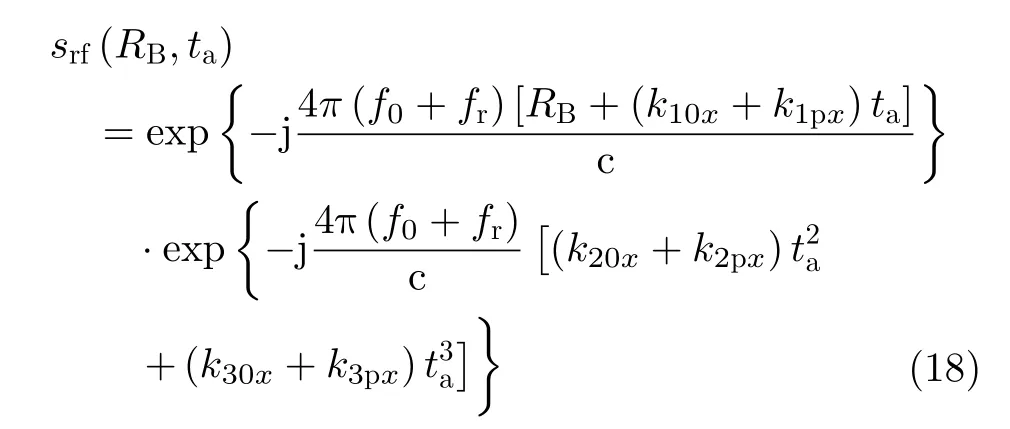
3.2.2 基于方位速度等效变换的距离弯曲校正
经过式(18)的变化,去除了非方位向运动参数的影响,原本的3维加速运动模型变换成了方位向直线非匀速运动,本节通过方位向速度等效变换,实现方位向运动带来的距离弯曲校正。首先将非匀速等时间间隔采样等效成匀速非等时间间隔采样,计算等效匀速速度, 其中Na表示方位向慢时间的采样点数, xR(1)和 xR(Na)分别表示成像时间内平台x方向的起始坐标和终止坐标

根据传统匀速直线运动模型中距离徙动的计算可知,在等效匀速运动状态下,距离徙动量可以表示为

其中,Rb表示孔径中心处的斜距,正侧视下表示为
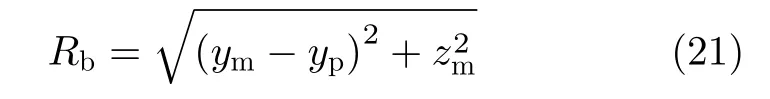
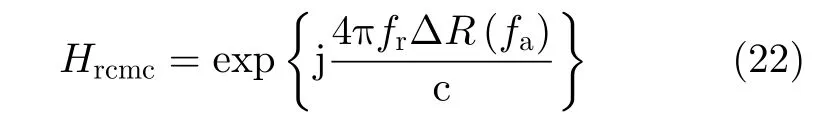
根据式(21)可以构建2维频域内的方位向运动带来的距离弯曲校正函数,表示为对经过非方位向相位补偿后的式(18)进行2维FFT运算,然后与式(22)相乘就可以实现方位向运动造成的距离徙动校正。
3.2.3 基于非均匀傅里叶变换的方位压缩
为进行方位向的压缩,继续利用上节的等效速度v ¯x, 同时计算等效非等时间间隔的方位向时间tu
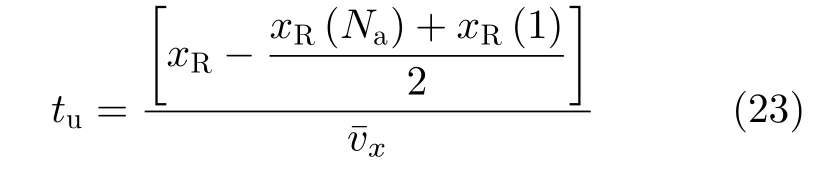
利用非均匀傅里叶变换将补偿后的信号变换到方位频域

经过非匀速等时间间隔采样向匀速非等时间间隔采样的等效变换,可以根据等效匀速运动过程构建方位向压缩函数,其中Ka表示方位调频率

将式(24)与式(26)相乘,并进行方位向逆傅里叶变换即可得到方位压缩结果。将压缩后的结果变换到时域即可得到成像结果
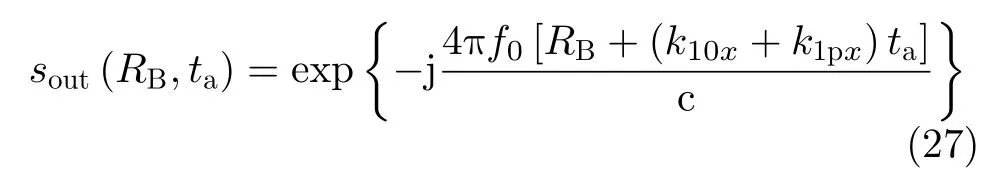
基于方位向运动信息分离的成像处理过程可分为4个步骤:
(1)距离压缩:此过程主要是完成回波信号的距离压缩,是在距离时域内实现的。
(2)基于非方位向运动信息分离的相位补偿:此过程主要完成非方位向运动对成像影响的校正,是在距离时域内完成的,补偿因子为H1(fr,ta)。
(3)基于方位向速度等效的距离弯曲校正:此过程主要完成方位向运动对成像造成的距离弯曲校正,是在2维频域内实现的,校正因子为Hrcmc。
(4)基于非均匀傅里叶变换的方位压缩:此过程主要是解决方位向非匀速运动带来的方位向压缩问题,是在方位频域内实现的,方位向压缩因子为H2(fa,ta)。
具体的处理过程如图2所示。
4 机动SAR成像算法仿真验证

图2 机动SAR方位向运动信息分离成像处理流程图
本节通过仿真方法验证聚束模式下机动SAR方位向运动信息分离成像算法的有效性,仿真模型为3维匀加速运动。仿真参数如下:载频为1.5 GHz,脉宽为5 μs,带宽为150 MHz,方位向慢时间为4 s。根据雷达参数可知,距离向分辨率的理论值为1 m,方位向分辨率由等效速度v ¯x和 等效调频率Ka按照传统匀速直线运动近似得到,不同的等效速度有不同的分辨率结果,约为1 m。雷达初始位置(xm,ym,zm)为(–200 m, 1000 m, 4000 m)。
4.1 单点目标仿真
以无人机载机动SAR为例,如图3所示,为单点目标仿真结果,属于爬升转弯运动或者俯冲转弯运动。采用的速度参数为vx0=100 m/s, vy0=5 m/s,vz0=3 m/s , ax=0.1 m/s2, ay=−0.5 m/s2, az=−0.5 m/s2。目标点的位置为(0 m, 0 m, 0 m),方位向成像时间为4 s。
4.2 多点目标仿真

图3 3维匀加速运动下的单点目标仿真
仿真时,选取5个点目标,其坐标为(–50 m,0 m, 0 m), (0 m, –50 m, 0 m), (0 m, 0 m, 0 m),(0 m, 50 m, 0 m), (50 m, 0 m, 0 m)。如图4为3维匀加速运动模型下的多目标成像结果。在仿真中,采用的速度参数为 vx0=100 m/s , vy0=−20 m/s,vz0=−6 m/s, ax=0.2 m/s2, ay=3 m/s2, az=1 m/s2。
从上述实验结果中可以看出算法在3维匀加速运动的成像中,具有很好的效果。从图4(c)和图4(d)可以看出,算法对机动SAR成像的距离徙动和方位向距离弯曲校正有较好的效果。
5 空变性校正与分析
空变性问题是机动SAR成像需要解决的另一个关键问题。本文主要通过对大成像场景的小区域划分解决空变性问题,即通过在不同的小区域内选择不同的成像参考点,实现空变性问题的解决。这种方法是一种简单快捷的方法,主要是将大成像场景划分成若干个小成像区域,分别在各个小成像区域内选取运动参数和参考点,进行成像分析。
如图5到图7所示为仿真验证,以及与相位滤波校正算法[15]的对比验证。在仿真中,采用的无人机平台的运动参数为vx0=100 m/s , vy0=5m/s, vz0=3m/s , ax=0.1 m/s2, ay=−1 m/s2, az=−0.5 m/s2。目标点的位置为(1000 m, 500 m, 0 m),方位向成像时间为5 s。图5(a)表示成像剖面图;图5(b)表示方位向主副瓣分析;图5(c)表示距离向主副瓣分析。
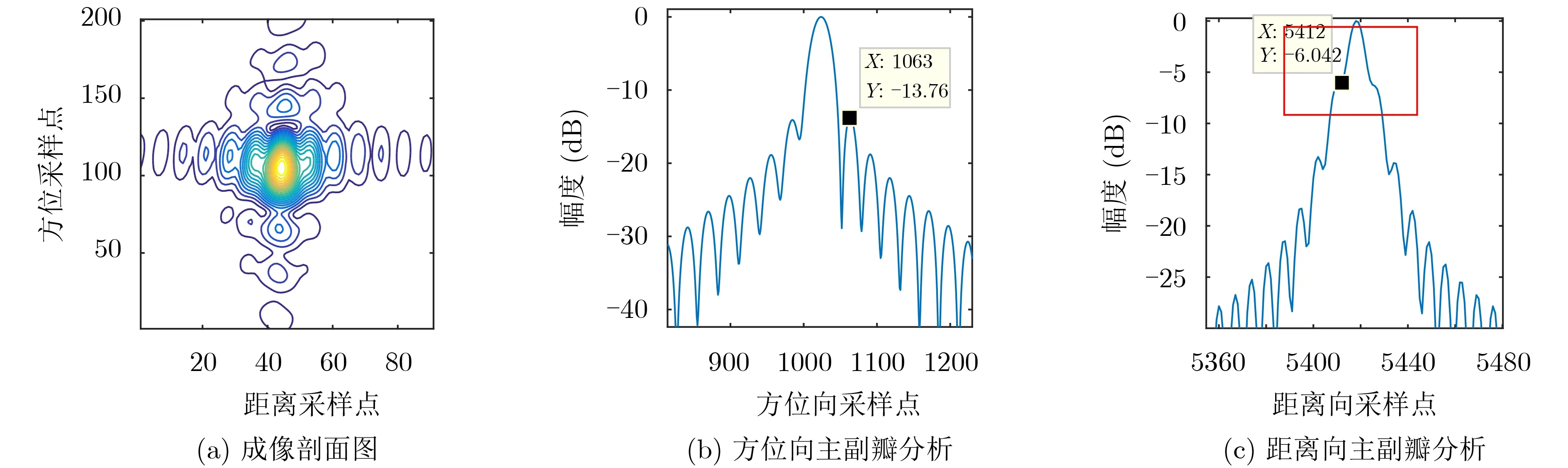
图5 未进行空变性校正的成像结果
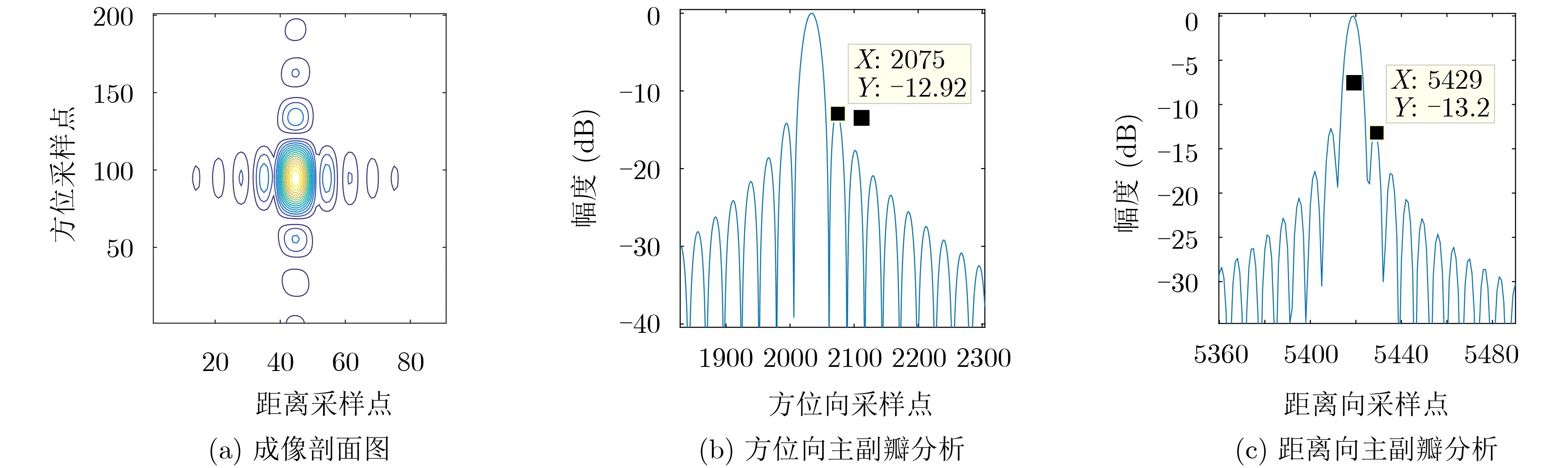
图6 基于子图像划分成像的空变性校正成像
图7 基于频域相位滤波的空变性校正成像结果
图5表示的是未经过空变性校正的机动SAR成像结果。图6采用子图像划分成像的方法,将大成像区域划分成若干小成像区域,然后依据不同的中心参考点进行成像的结果。图7表示采用频域相位滤波进行空变性校正的结果。从图5(b)可以看到较为明显的不对称性,图5(c)中方框内的阶梯形变化则显示了空变性造成的主瓣展宽。对比图5和图6、图7可以发现,经过后两种方法处理,都可以较好地实现机动SAR的空变性校正;采用子图像处理的方法更为简单快捷,成像效果也最好;采用频域相位滤波的方法能够处理较长孔径的数据。但是,孔径时间变长处理效果依旧会变差,这是由于在运算过程中进行了近似处理。
6 结束语
传统SAR成像需要平台保持匀速直线运动,针对传统算法不能满足SAR在作战条件下,适用于机动灵活的平台运动的要求,提出一种基于方位向运动信息分离的成像算法,通过分离非方位向运动信息对成像的影响,将不同模型下的成像等效成方位向直线非匀速运动成像。相比传统运动误差补偿算法,该算法能够适应更强的速度变化和运动变化。同时,利用3维同性的特点,丰富了斜距信息,能够为后续的目标识别提供更多的选择。该算法不依赖于传统频域算法对2维频谱的求解,扩展了频域成像算法对模型的适用性,减少了传统SAR成像的“工作状态盲区”。最后,通过不同运动模型下的仿真验证了算法的可行性、有效性。
