基于FW-PSO算法优化无线传感网络拓扑结构的方法
2021-03-17杨广媛
张 颖 杨广媛
(上海海事大学信息工程学院 上海 201306)
1 引言
无线传感网络(Wireless Sensor Network,WSN)[1]具有较高的抗毁性是各种实际应用中的一项重要需求。由于应用环境复杂,无线信号的传输极易发生中断、衰变等状况;另一方面,网络节点很容易受到恶意攻击或由于能量耗尽而导致网络拓扑分区,大大降低网络的连通性及覆盖范围,甚至会使整个网络瘫痪[2,3]。因此如何提高网络的抗毁性是WSN部署实施的关键问题。
现实世界中的网络都可以用复杂网络来表示。复杂网络中的无标度网络[4]对于随机攻击具有很强的抗毁性,但对故意攻击是脆弱的。其度分布近似服从“幂律分布”[5],故节点度小的节点占大部分,节点度大的节点占少数,但节点度较低的节点失效对网络的连通性影响并不明显。显然,构造具有无标度特性的WSN拓扑能够使其具有更强的抗毁性。
网络抗毁性分为静态抗毁性和动态抗毁性,其中动态抗毁性又称为级联抗毁性。如果一个传感器节点在WSN中失效会导致负载重新分配到相邻节点,不断增加的负载可能会导致整个网络出现级联问题,这将严重影响网络的性能,甚至会导致整个网络崩溃。在设计WSN的拓扑结构时,不仅要考虑网络性能,还要考虑级联故障。Motter等人[6]提出了级联失效的简化模型,分析了产生级联失效的原因。文献[7]进一步发现无标度网络的级联故障具有幂律特征。崔文岩等人[8]为了控制复杂网络中级联失效的扩散,提出了节点度和介数中心性相关的边缘加权模型。由于网络的节点和链路具有处理和传输数据的作用,一个链路或部分节点的故障会导致负载重新分配,进而导致其他节点的故障,但是进一步的负载重新分配将导致级联故障,于是Wang等人[9]研究了负载重新分配对抗毁性的影响。文献[10]提出一种基于非均匀负载再分配的级联故障模型。Ren等人[11]提出了另一种基于节点剩余能量的级联故障模型,该模型在负载重新分配时考虑到节点的剩余能量。尹荣荣等人[12]提出了一种基于可变负载和节点固定容量的级联故障模型,并求解出网络级联故障时负载的临界值。李黎等人[13]提出了一种基于有限资源来添加边的网络拓扑重构办法。以上研究都依赖于优化节点性能来控制级联故障,有的只注重研究单一节点或边受到攻击无法通信的情况,有的只分析网络的静态连接性能,并没有考虑在网络级联故障下如何构造强连通性及强抗毁性的拓扑结构。本文考虑网络的动态特性,通过智能优化算法构造具有最强连通性的网络拓扑结构,研究其优化后的网络在级联故障情况下的抗毁性能。
本文首先构建具有无标度特性的WSN,并提出了一种FW-PSO(FireWorks and Particle Swarm Optimization)算法,通过对模型变量和约束条件做适当的改变,将FW-PSO算法应用于具有无标度特性的WSN,对网络拓扑进行优化,并在不同攻击策略下对优化后的网络进行静态抗毁性和动态抗毁性分析。仿真实验表明,优化后的网络在遭受级联故障和随机故障时抗毁性明显提高。文章结构如下:第2节主要介绍级联故障模型的构建;第3节主要介绍提出的FW-PSO算法及基于该算法优化具有无标度特性的WSN拓扑结构的具体过程;第4节为仿真实验及结果分析;第5节对本文进行总结。
2 级联故障模型
在网络中,当一个节点发生故障时,未处理的数据将被重新分配给其邻居节点。为了维护网络流量,避免网络拥塞,高容量的邻居节点将被重新分配更多未处理的数据。因此,本文使用故障节点负载优先重分配原则的级联失效模型,其中节点的初始负载[14]被设置为节点度的函数。
(1) 将网络中节点j的初始负载Lj与它的节点度kj的函数关系定义为

其中, α ,β控制着节点初始负荷的强度,均为可调参数。节点的度 kj表示与该节点相邻的节点个数,即连接该节点的边的数目。
(2) 节点i的负载按照优先原则重新分配给邻居节点j,节点负载重分配原则描述为

其中,Γi为节点i上所有邻居节点的集合。
根据负载重新分配的原则,当节点i失效后节点j从i接收到的附加负载∆ Lij为

可以看出节点j接收到的额外负载∆ Lij中与参数 β的选择无关,故在仿真实验中不对β 进行设置。
(3) 节点容量C aj反映了负载的承载能力,并且受到网络成本的约束。假设节点j的容量与其初始负载成正比,则C aj描述为
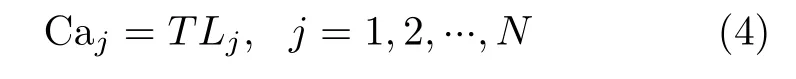
式中,T ≥1,为故障容忍参数。如果节点j接收到超出其容量的额外负载,即Lj+∆Lij>Caj,则节点j将失效。节点j的故障导致进一步的负载重新分配,这可能触发其他节点的故障并导致级联故障。
本文中采用C Fi表示节点i所导致的失效节点的数量[15],显然0 ≤CFi≤N −1,为了量化节点受到袭击后导致的网络全局级联故障的程度,采用了节点遭受袭击后的归一化指标,即

其中,A表示遭受袭击节点的集合,NA表示遭受袭击节点的数量。
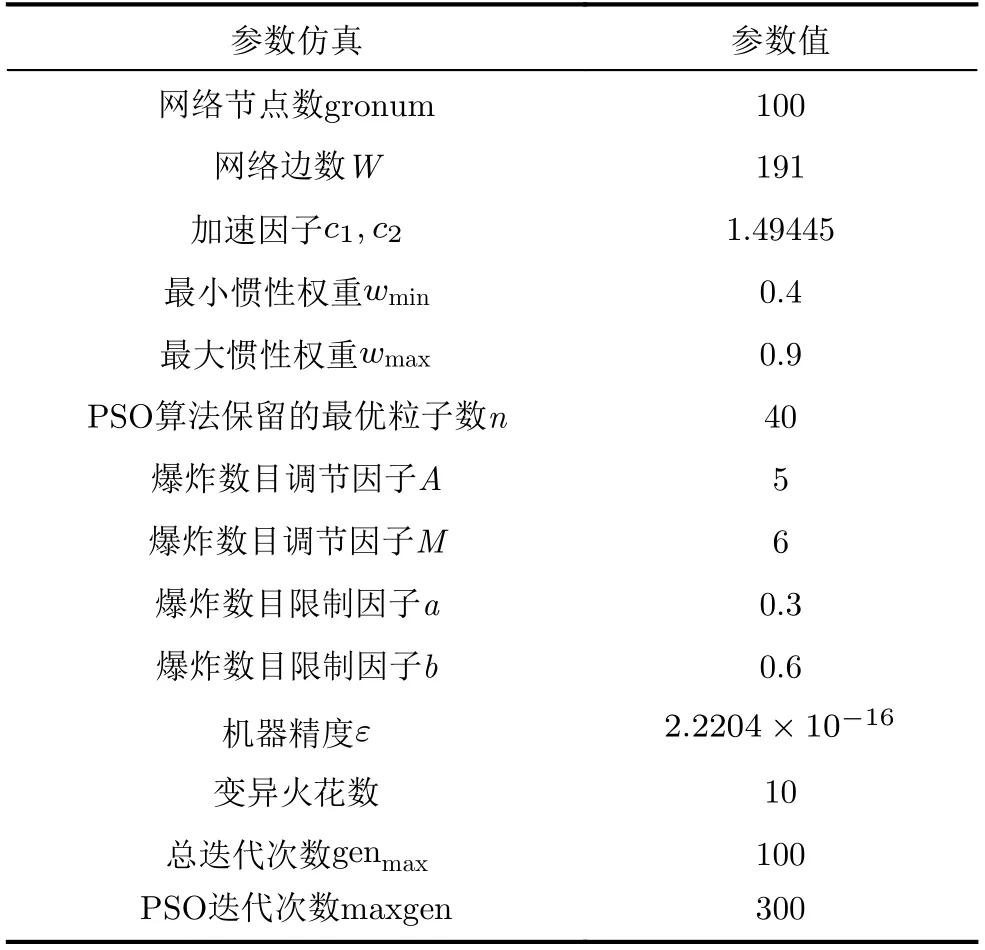
分析以上模型可知容忍参数 T 的大小直接影响网络是否故障。当 T很大时,任一节点的失效都不能导致级联故障。当 T很小时,任一节点的失效都会导致网络瘫痪。所以,网络存在着一个从自由态到拥塞态的转变,转变点就是关键阈值 Tc。当T >Tc时,网络中的每个节点都能够处理来自其他节点的额外负载,不会出现级联故障的现象,网络能够正常运行。但当T 显然 Tc是网络避免级联故障的容忍能力的最小值。Tc的值越小,网络在发生级联故障时的抗毁性就越强,所以关键阈值Tc能够很好地反映出网络的级联抗毁性。 3.1.1 PSO算法 在PSO(Particle Swarm Optimization)算法[16]中,如果粒子群的总数为n,搜索空间是D维,第i个粒子的位置表示为Xi=(xi1,xi2,···,xiD),速度变化率为Vi=(vi1,vi2,···,viD)。第i个粒子目前搜索到的最优位置为Pi=(pi1,pi2,···,piD),整个粒子群目前搜索到的最优位置为 Pg=(pg1,pg2,···,pgD),单个粒子每一步迭代的速度和位置则可表示为 其中, c1, c2为加速因子,均为常数。r1, r2为在[0,1]之 间的随机数。w 采用线性递减权值策略。定义为 其中, wmin为最小惯性权重,wmax为最大惯性权重, iter为 当前迭代次数,i termax为该算法迭代的总次数。 3.1.2 烟花算法 烟花算法[17]主要由3部分组成:爆炸算子、高斯变异算子和选择策略。假设烟花数量为Num,第i个烟花xi的爆炸半径Ai和 爆炸火花数目Si分别如式(9)、式(10) 其中,A和M均为常数,分别用来调整烟花的爆炸半径大小和产生的爆炸火花数目。f (xi)表 示烟花xi的适应度值,ymin=min(f(xi)),ymax=max(f(xi))。ε是机器精度,用来避免除以零的操作。其中,Si的边界定义为 式中,a, b为爆炸数目限制因子,均为常数。 为了增加爆炸烟花的多样性,引入高斯变异操作。烟花xi在维度k上执行高斯变异操作的方式为 其中,e表示均值和方差均为1的高斯分布。 在经过上述步骤产生爆炸火花和高斯变异火花后,将从所有的烟花、爆炸火花和高斯变异火花中选择一定数量的个体作为下一代烟花进行迭代。其中,适应度最好的被选入下一代,剩下的Num–1个烟花采用轮盘赌的方法进行选择,如式(13)、式(14) 其中,K表示所有烟花和两种火花(爆炸火花和高斯变异火花)的集合,R (Xi)表示当前个体到剩余其他个体之间的距离之和。P (Xi)表示当前烟花被选择的概率。 对于PSO算法,粒子在其历史最优解和当前全局最优解的指导下,能够快速找到更好的解,收敛速度快。然而,粒子群中粒子位置主要通过比较其自身位置、周围位置和粒子群中的当前最佳位置更新,模式较单一,因此在后期迭代计算中收敛速度不高,极易陷入局部最优。在烟花算法中,烟花可以通过爆炸和突变操作在整个搜索空间中找到全局最优解。为了利用两种算法的优点,本文提出了一种FW-PSO算法,该算法主要分以下3步: 步骤 1 PSO算法在进化到maxgen代后,保留适应度最优的n个粒子,删除适应度较差的gronum-n个粒子,其中gronum为种群规模。 步骤 2 保留下来的n个粒子进行烟花算法的爆炸、变异和选择操作,得到gronum-n粒子。 步骤 3 PSO保留的n个粒子与经过烟花算法优化得到的gronum-n粒子合并形成新的粒子群继续进行下次迭代,直到达到总迭代次数g enmax。 3.3.1 无标度特性的WSN拓扑结构模型 将WSN用一个无权无向图G =(V,E)描述,其中V ={v1,v2,···,vN} 是 一 组 节 点,E ={e(vi,vj)}是一组边,N =|V|是 网络中的节点总数,W =|E|表示边的数量。为了对网络进行建模,给出以下定义。 定义1(邻接矩阵):定义A (G)=(aij)N×N表示图的邻接矩阵,那么图 G就可以用其邻接矩阵表示。其中,aij的 取值集合为{aij=aji=1|e(vi,vj)∈E(G)}和{aij=aji=0|e(vi,vj) ∈/E(G)}。 定义2(拉普拉斯矩阵):若L (G)∈R×RN是图G的拉普拉斯矩阵,则L (G)= Dˆ(G)−A(G),其中Dˆ(G)=diag{di}为节点的度构成的对角矩阵。记拉 普 拉 斯 矩 阵 L(G) 的 特 征 根 为µi, i =1,2,···,N。将特征值从大到小排序可得:µN≥µN−1≥···≥µ2≥µ1=0。 定义3(代数连通度):定义 µ =µ2,当且仅当µ>0 时图是连通的。µ 即为图的代数连通度。 节点 vi和vj之间的冗余路径越多,网络的抗毁性越强。为了度量网络中的冗余路径,需计算任一节点对{ vi,vj} 之间长度为l 的路径数目nlij,然后对其求和,如式(15) 为了进一步化简式(17),给出以下引理。 引理1设 nl表 示网络中长度为l的闭途径的数目,则 其中,λi为 邻接矩阵A (G)的特征根。 将式(18)代入式(17)得 将式(19)变换得到式(20),就得到图 G 的自然连通度如式(19) 约束条件如式(22) 3.3.2 FW-PSO算法求解过程 首先,根据“增长”及“择优连接”[5]特性构造具有无标度特性的WSN网络,得到其邻接矩阵A(G)。又由于FW-PSO算法适合求解连续优化问题,所以需要对拓扑优化模型做一个变量变换。具体操作如下: (1) 在式(22)中aij表示的是邻接矩阵A (G)的下三角矩阵(不包括对角线),即(i>j。 故将N(N −1))/2个元素重新排列记入 X =x1,x2,···,xN(N−1)/2中。xi是属于0或者1的,若令X′=g(X{), 那么g (X)表示的就是 X 到 X′的映射,可得:=0|xi<0.5 or=1|xi≥0.5}。 (2) 将变量转换为连续变量。上步得到的 X 中 M 根据上述分析,基于FW-PSO算法优化网络拓扑结构过程的伪代码如表1。 本小节为了验证3.3节提出的网络拓扑优化算法的有效性,用MATLAB R2016a进行仿真实验。假设网络监控区域为1 00×100 m2,参数设置如表2。首先构造初始WSN网络拓扑并得到其邻接矩阵A(G)。然后通过表2设置的参数进行FW-PSO算法的初始化。再根据3.2节的FW-PSO算法步骤,通过FW-PSO算法得到式(21)的最优值,即具有最大自然连通度的WSN网络拓扑,实验结果如图1。 表1 FW-PSO算法的伪代码 图1(a)比较了几种优化算法中自然连通度随着进化代数增加的变化情况,从图中可以看出随着迭代次数的不断增加,拓扑结构的不断优化,自然连通度会不断增加,FW-PSO算法的自然连通度最优值达到9.5526,标准PSO算法、差分进化算法(Differential Evolution algorithm, DE)及初始网络拓扑分别为:9.0486, 8.7691和1.7559。图1(b)单独给出了PSO算法和烟花算法(FireWorks algorithm,FW)的性能比较,其中FW的最优值为9.1930。从图中可以看出,两者在第130次迭代附近有个曲线交叉,在迭代优化前期PSO算法表现出了比FW算法更强的搜索优势,而在后期FW算法的优势较大,这是因为PSO算法在早期虽然收敛速度快,但是由于缺少有效的振荡和变异措施,使得该算法在后期收敛速度较慢,易陷入局部寻优;而FW算法通过爆炸和突变操作使得解的多样性获得提高,具有较强的全局搜索能力。上述表明,经过拓扑优化,网络的抗毁性不断增强,且本文提出的FW-PSO算法比标准PSO算法及DE算法收敛速度更快,寻优结果更好。 为了研究优化前后网络拓扑的抗毁性,本小节将从动态抗毁性和静态抗毁性两方面分析。首先选择攻击策略为度大袭击(High-Degree, HD)和度小袭击(Lowest-Degree, LD),分析优化前后的网络抵御级联故障的能力,即动态抗毁性。度大袭击为袭击网络中度大的节点,度小袭击为袭击网络中度小的节点。然后,还分析了网络受到随机攻击时的静态抗毁性。 表2 仿真参数设置 图1 自然连通度随迭代次数变化情况 4.2.1 动态抗毁性 根据第2节提到的级联故障模型,分析优化前及由FW-PSO算法,PSO算法和DE算法优化后的网络拓扑在HD和LD这两种袭击策略下的阈值 Tc。为了避免偶然性,进行10次重复实验,取其平均值。对 α>1, α<1及α =1, 3种情况下进行抗毁性分析。结果如图2。 从图2(a)中可以看出α <1时,HD攻击时优化前的关键阈值 Tc为1.2,经过DE算法,PSO算法和FW-PSO算法优化后的网络的 Tc分别为1.14, 1.12和1.08; LD攻击时优化前的关键阈值 Tc为1.38,经过DE算法,PSO算法和FW-PSO算法优化后的网络的Tc分别为1.34, 1.31和1.28。图2(b)显示,α=1时,HD攻击时优化前的关键阈值 Tc为1.32,经过DE算法, PSO和FW-PSO算法优化后的网络的Tc分别为1.15, 1.13和1.10;LD攻击时优化前的关键阈值 Tc为1.33,经过DE算法,PSO算法和FW-PSO算法优化后的网络的 Tc分别为1.25, 1.22和1.20。图2(c)显示,α >1时,HD攻击时优化前的关键阈值 Tc为1.30,经过DE算法,PSO算法和FW-PSO算法优化后的网络的 Tc分别为1.22, 1.18和1.10;LD攻击时优化前的关键阈值 Tc为1.20,经过DE算法,PSO算法和FW-PSO算法优化后的网络的 Tc分别为1.18, 1.16和1.14。显然,无论在 α取何值的情况下,经本文所提出的FW-PSO算法优化后的网络在遭受到HD或LD攻击时的抗毁性都获得明显提高,且FW-PSO算法比DE算法和PSO算法对网络抗毁性的提升效果更好。 图2 α不同时,4种方法的抗毁性对比 4.2.2 静态抗毁性 为了更好地验证优化后网络的性能,分析在随机攻击下的静态抗毁性,给出了网络整体效率的概念,定义如式(23) 其中,lij为 节点i和j 之间的最短路径。上式在任何情况下都能够测度网络在受到攻击时的网络整体连通性。 图3 随机攻击时网络连通性对比 仿真实验结果如图3,从图中可以看出,优化后的网络在遭受到随机攻击时的连通性比优化前有了很大改进,说明优化后的网络抗毁性明显增强。随着随机攻击节点数的上升,网络系统的整体连通性不管对于初始网络还是几种算法优化后的网络都有下降的趋势,但是FW-PSO算法下降得最为缓慢,且始终保持较高的网络整体连通度。FWPSO算法优化后的网络比PSO算法和DE算法优化后的网络在面对随机故障时,网络的连通性更高,即FW-PSO算法较PSO算法和DE算法优化后的网络及未优化的初始网络在遭受随机攻击时拥有更好的抗毁性能,具有较佳的网络静态抗毁性。 本文提出了一种针对WSN的FW-PSO网络拓扑优化算法,该算法融合了烟花算法种群多样性和PSO算法搜索能力强的优点,具有较高的收敛速度和搜索性能。构建了具有无标度特性的WSN,并以自然连通度为寻优函数建模,通过变量变换,将FW-PSO算法运用到WSN网络拓扑优化中。通过实验分析了算法优化后网络的动态和静态抗毁性。仿真实验表明,本文所提算法对WSN网络拓扑优化后在网络动态和静态抗毁性上取得明显提升效果。3 基于FW-PSO算法优化具有无标度特性WSN拓扑的过程
3.1 PSO算法与烟花算法概述


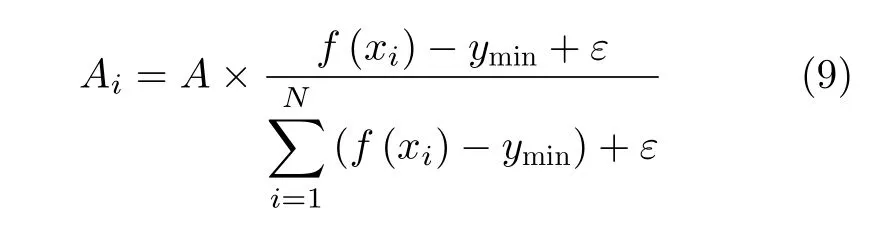
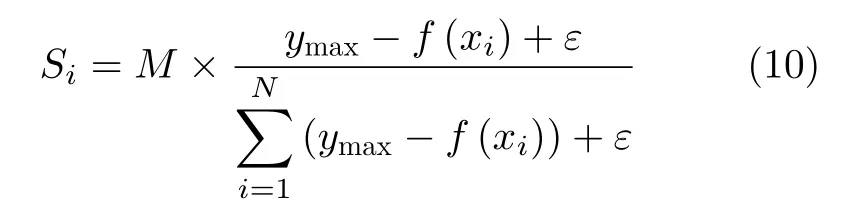
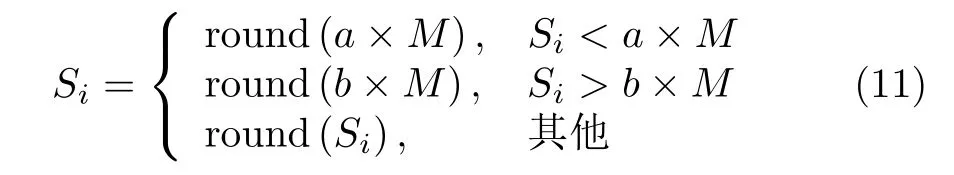

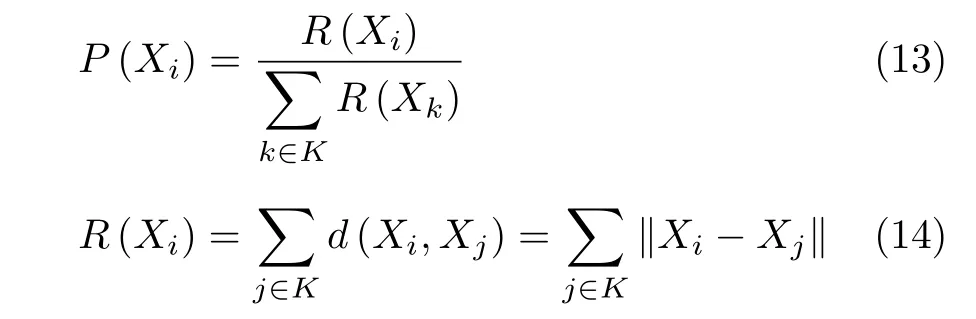
3.2 FW-PSO算法
3.3 无标度特性的WSN拓扑结构模型及优化求解过程




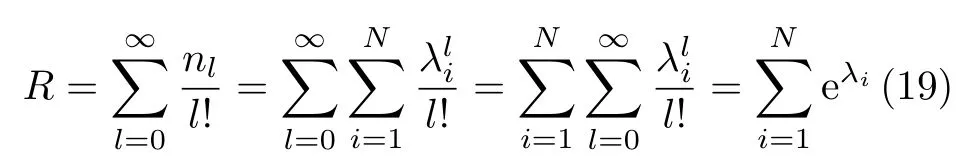

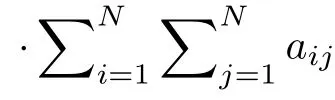



4 仿真实验及分析
4.1 优化拓扑结构的实验仿真

4.2 抗毁性分析


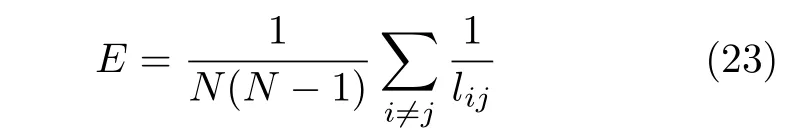

5 结论
