基于切比雪夫-迹迭代的大规模MIMO系统软输出信号检测

景小荣 文晶晶 雷维嘉②

①(重庆邮电大学通信与信息工程学院 重庆 400065)

②(移动通信技术重庆市重点实验室 重庆 400065)

1 引言

大规模多输入多输出(Multiple-Input Multiple-Output，MIMO)系统[1]由于基站端部署了大量的天线，给上行信号检测算法设计带来了严重的挑战。最大似然(Maximum Likelihood, ML)算法作为MIMO检测算法中的最优算法，其计算复杂度随发送天线数和调制信号阶数的增长呈指数规律上升，因此在实际系统中难以应用。于是，似然上升搜索 (Likelihood Ascent Search, LAS)算法[2]和主动禁忌搜索(Reactive Tabu Search, RTS) 算法[3]被提出用于大规模MIMO信号检测，然而，当系统采用高阶QAM调制时，两者性能并不理想。文献[4]提出一种改进的BP算法。然而，这些研究通常假设基站天线数 N 与用户数 K相等。在实用大规模MIMO系统中，受导频污染制约，用户数只能远小于基站天线数(假设用户配置单天线)，即系统负荷系数K /N ≪1。 而当K /N ≪1时，线性检测算法，例如迫零(Zero-Forcing, ZF)[5]和最小均方误差(Minimum Mean Square Error, MMSE)检测算法，可取得接近ML算法的性能；然而这两种算法涉及高维矩阵求逆运算，其复杂度约为O (K3)。于是，文献[6–9]则分别采用Neumann级数、牛顿迭代法和共轭梯度(Conjugate Gradient, CG)法和并行切比雪夫迭代(Parallelizable Chebyshev Iteration,PCI)方法来代替均衡矩阵求逆。

然而，随着5G技术的推进，未来无线通信要求提供更高的频谱效率，因此，格雷编码的具有正方形星座图的高阶正交幅度调制(Higher Quadrature Amplitude Modulation, HQAM)，比如256-QAM，因其同相和正交相具有对称性，调制和解调相对简单而被纳入5G标准规范。然而，HQAM由于调制星座图上信号点距离的急剧缩小又给信息比特的恢复带来严重的挑战，因此通常借助信道编码的软输出信息来获得可接受的检测性能。文献[10]基于高斯-希尔德迭代(Gauss Seidel Iteration, GSI)，提出一种低复杂度软输出信号检测算法；然而该算法采用较为低阶的调制模式，同时Max-Log-MAP算法被用于计算编码比特的对数似然比(Log-Likelihood Ratio, LLR)。对于HQAM, Max-Log-MAP算法将引起过高的计算复杂度。

在上述分析的基础上，本文针对大规模MIMO上行链路，基于MMSE准则，提出一种基于切比雪夫-迹迭代(Chebshev Trace Iteration, CTI)的低复杂度的软输出信号检测算法。与文献[9]方法不同，为了加快算法收敛速度，本文所提CTI算法是在迹迭代(Trace Iteration Method, TIM)算法[11]的基础上，结合Chebyshev方法而形成的；同时，在软信息计算方面，利用格雷编码调制信号的比特翻转特性，文中给出了一种新的LLR简化计算方法。数值仿真验证了本文所提软输出信号算法的有效性。

2 系统模型

考虑多用户大规模MIMO系统上行链路。假设基站配置 N 根天线，为 K个单天线用户同时提供服务，满足N ≫K 。 K个用户待传输的信息比特，分别经过各自的信道编码器和格雷编码的 22m-QAM调制器，形成 K×1 维发送符号矢量xc，满足E(xcxcH)=IK。在接收端，基站接收到的N ×1维信号yc可表示为

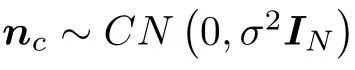
3 问题提出

采用MMSE接收，发送信号矢量xc估计值

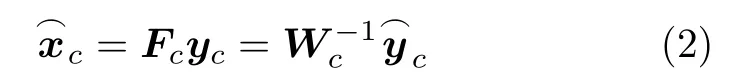
其中， Gc=Hc。令Uc=1Gc表示等效信道增益矩阵，则xc中第k 个符号的估计值

其中， µk表 示Uc中第( k,k)个 元素，即均衡后与xc,k对应的等效信道增益，c,k表示MMSE均衡后c,k中所包含的噪声加干扰项(Noise Plus Interference,NPI)，其对应方差为

其中，Uzk和 Ekk分 别表示Uc中 第( z,k)个元素和矩阵Ec=1Gc1中第( k,k)个 元素，k ,z=1,2,···,K。根据Max-Log-MAP准则，c,k中 的第b 个编码比特的LLR为

其中，γk=/表示第k 个用户的信干噪比(Signalto-Interference-plus-Noise Ratio, SINR),和分别表示第 b位为0 和1 的Q A M 调制符号集合，b=1,2,···,2m。

根据上述分析，求解MMSE均衡矩阵Fc和均衡后的等效信道增益矩阵 Uc及矩阵Ec均涉及1的计算，其计算复杂度高达 O(K3)；同时，对采用22m-QAM的多用户大规模MIMO系统，采用Max-Log-MAP算法计算用于信道译码的LLR，将涉及高达 O (K·2m·22m)的计算复杂度。为此，下面将给出一种低复杂度软输出信号检测算法。

4 基于切比雪夫-迹迭代的低复杂度软输出信号检测算法

本节首先给出基于CTI的大规模MIMO信号检测过程；接着分析了Max-Log-MAP算法计算LLR存在的问题；进而结合格雷编码的调制符号的比特翻转特性和二叉树结构，给出了一种融合三叉链表搜索的LLR简化计算方法；最后，对算法复杂度进行了分析。

4.1 CTI用于线性方程组求解

当矩阵 A为对称正定时，给定初始解向量，可利用CTI实现线性方程组 A x=b ≠0的迭代求解，而无需对矩阵 A进行求逆操作。

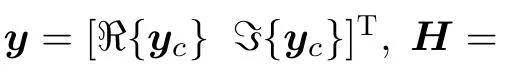
其中，x =[ ℜ{xc} ℑ{xc} ]T( 其中元素为 2m-PAM符号)，ℜ {·}和 ℑ {·}分别表示取实部和虚部。

确定初始解后，则采用CTI来迭代求解 x， 具体迭代过程如式(9)所示

其中，λt+1=2fCt(f)/Ct+1(f), Ct+1(f)=2fCt(f)−Ct−1(f)为 切比雪夫多项式，T r(W) 表示矩阵W 的迹， f=1/|1−w·ηmin/Tr(W)| , w=2Tr(W)/(ηmax+ηmin), ηmax和 ηmin分 别表示矩阵W 的最大特征值和最小特征值，具体定义见文献[13]， t=1,2,···,T,T表示最大迭代次数。

观察上述过程，利用CTI思想实现发送向量x 的迭代估计，而无需计算矩阵W 的逆。

4.2 基于传统的Max-Log-MAP算法的LLR计算

由x=W−1，则在第t 次迭代结束后，存在收敛到x 时 ，也将对应收敛于矩阵W−1。 由x(t)=则对应地由式(10)迭代求解

4.3 LLR简化计算方法

4.3.1 MMSE扩展预处理

对信道矩阵 H 、接收信号矢量y 和噪声矢量n进行扩展，即令

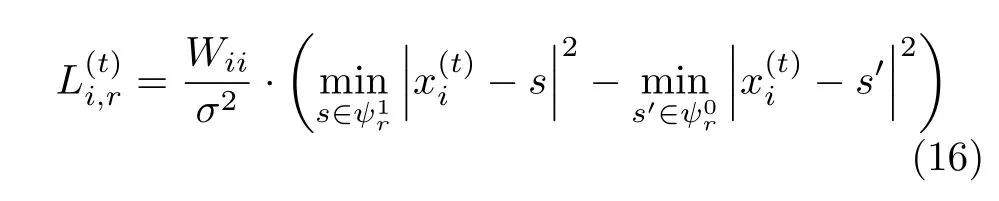
4.3.2 基于Max-Log-MAP算法的LLR简化计算

Max-Log-MAP算法按照式(16)计算各用户编码比特的LLR所需计算量为 O (2K·m·2m)，对于采用HQAM的多用户大规模MIMO系统来说，该计算量将构成软输出信号检测算法中的主要部分。于是，下面将给出一种LLR简化计算方法。

引理1[15]由格雷编码的比特矢量(bm,bm−1,···,b1)映射成P A M 信号，其第 l比特的翻转次数为TC(l)=2m−l(不考虑最高位比特返回原始比特状态)，其中l =1,2,··· ,m。

由引理1，根据br∈{0,1}的比特翻转特性，格雷编码的 2m-PAM的 2m符号被分割成2m−r+1个集合，每个集合由 2r−1个 符号组成，以来表示由比特br确 定的第Br个集合，其中r =1,2,···,m。图1描绘了格雷编码的16-PAM符号集合划分过程，其中五角星代表，方形代表硬判决结果sML，三角形代表。

如果令由 2m个 2m-P A M 符号组成的集合+1表 示根结点，即第1结点层，Bm+1=0，则在第m −r+2 结点层，2m−r+1个集合分别代表2m−r+1个 子结点，于是 2m-PAM符号集合的递归分割结果可用一满二叉树来表示(图1中黑色虚线所示)，而对内存需求非常小的三叉链表恰好可用来存储二叉树。根据二叉树和三叉链表之间的对应关系，文中用同样也表示三叉链表中结点，只不过对于三叉链表中的结点， 其包含3个指针域和2个数据域，其中3个指针域分别为该结点的左孩子指针(Lchild)、该结点的右孩子指针(Rchild)和该结点的父指针(Parent)，而2个数据域分别为Br的数值及其奇偶性(Parity)，其中Br∈{0,1,··· ,2m−r+1−1}。三叉链表中结点的结构如图2所示。特别说明，对于根结点+1，其数据域为空集，Parent为空指针，而对于叶子结点，Lchild和Rchild均为空指针。

图2 三叉链表结点示意图

由前述知：将信号模型从复数域转化到实数域，等效于将 22m-QAM分解为两路相互正交的同相和正交相 2m- PAM。对于 2m-PAM信号，其信号空间由 2m−1个 幅度阈值− (2m−2)d , − (2m−4)d,···,(2m−4)d , ( 2m−2)d 划分成 2m个间隔。因此，可采用二分法通过 m次比较就可确定所处的区间，进而得到 sML及其在 2m-PAM符号集合中的下标 qML；同时，与sML对应的格雷编码比特向量b∗=(−1···)也相应地确定下来。

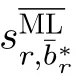
综合4.1节和4.3节的分析，表1给出基于CTI的软输出信号检测算法的步骤，其中式(1)—式(6)为基于CTI的信号检测过程，式(7)—式(20)则为LLR简化计算过程。

4.4 算法复杂度分析和对比

以浮点运算数，对本文提出的基于CTI的软输出信号检测算法(仿真图中用CTI来标识)的复杂度进行分析，同时将其与基于Cholesky分解的软输出MMSE算法，基于Neumann级数展开的软输出MMSE检测算法[6]、基于CG的软输出MMSE检测算法[8]、基于GSI的MMSE软输出检测算法[10]进行对比(以Cholesky,Neumann,CG和GSI来标识)。由于基于MMSE准则的对比算法和本文所提基于CTI的软输出信号检测算法都必须计算滤波矩阵W 和匹配滤波输出信号，故该部分计算复杂度在分析中不予考虑。

表1 基于CTI的软输出检测算法的步骤

基于CTI的软输出信号检测算法的计算复杂度主要来源于以下3部分：

第1部分确定初始解 x(0)涉 及计算D−1、矩阵D−1与 向量的乘法，其所需浮点数为 4K；而确定x(1), T r(W), w , ηmax, ηmin及 f 所需浮点运算数依次为12K2+4K+1, 2 K −1, 3, 5, 5和4(计算x(1)采用类似于文献[9]的方法，将矩阵与矩阵间的运算调整为矩阵与矢量间的运算，以减小计算复杂度，后面对x(t)的计算采用类似操作。)W x =。在第t 次迭代需要计算Ct+1(f), λt+1，进

第2部分是采用CTI迭代求解线性方程组而计算x(t+1)， 因此，第t 次迭代共需8K2+8K+6次浮点运算。

第3部分是LLR简化计算。在迭代信号检测完成后，计算各用户编码比特的LLR需确定 sML和sqr∗，对于sML只需采用简单的二分比较法就可确定，故不计入运算量。对于 K个用户所包含的2Km 编码比特，确定sqr∗所需浮点运算数为4 Km；计算式(17)，还需1 0Km+5K次浮点运算，因此，LLR 简化计算所需浮点运算量为1 4Km+5K。

由后续仿真可知，CTI算法在迭代次数T =3时趋于收敛，因此，图3给出CTI, CG, GSI算法在T =3 , Neumann算法在Neumann序列级数TN=3的计算复杂度对比，图3中同时也给出了Cholesky算法的复杂度。由图3可知，本文所提CTI算法的计算复杂度远远小于其它对比算法，这主要是本文提出的软输出信号检测算法不但通过CTI避免了高维矩阵逆，而且还对LLR计算进行了简化，其中简化LLR计算对于降低整个软输出信号检测算法的计算复杂度起主要作用。

图3 各种算法浮点运算次数与用户个数的关系(256-QAM)

5 仿真结果及分析

采用蒙特卡洛仿真来验证文中提出基于CTI的MMSE软输出信号检测算法的性能。仿真中，信道编码采用码率为1/2，生成码字为[ 133o177o]的标准卷积码，调制模式为256-QAM，用户平均发送功率设定为1。接收端基站采用软输入维特比译码方法进行译码。

在N =128, K =16，图4给出本文提出的基于CTI的软输出信号检测算法的收敛性能图。由图可知，随SNR递增，CTI算法的BER明显降低，但当迭代次数 T ≥3时，其性能曲线基本趋于平稳，即算法实现收敛，因此，在图3和后续仿真中我们选择迭代次数T =3。

在 N =128, K =16，图5给出CTI算法与GSI,CG, Neumann, Cholesky算法的BER性能随SNR变化的对比图。由图5中可知，随SNR增加，各算法BER均逐渐减小；然而由于本文所提CTI算法采用了Chebshev加速，提升了整个算法的收敛速度，因此，在T =3下CTI算法相比于CG, GSI, Neumann 3种检测算法，更加逼近Cholesky算法的性能。

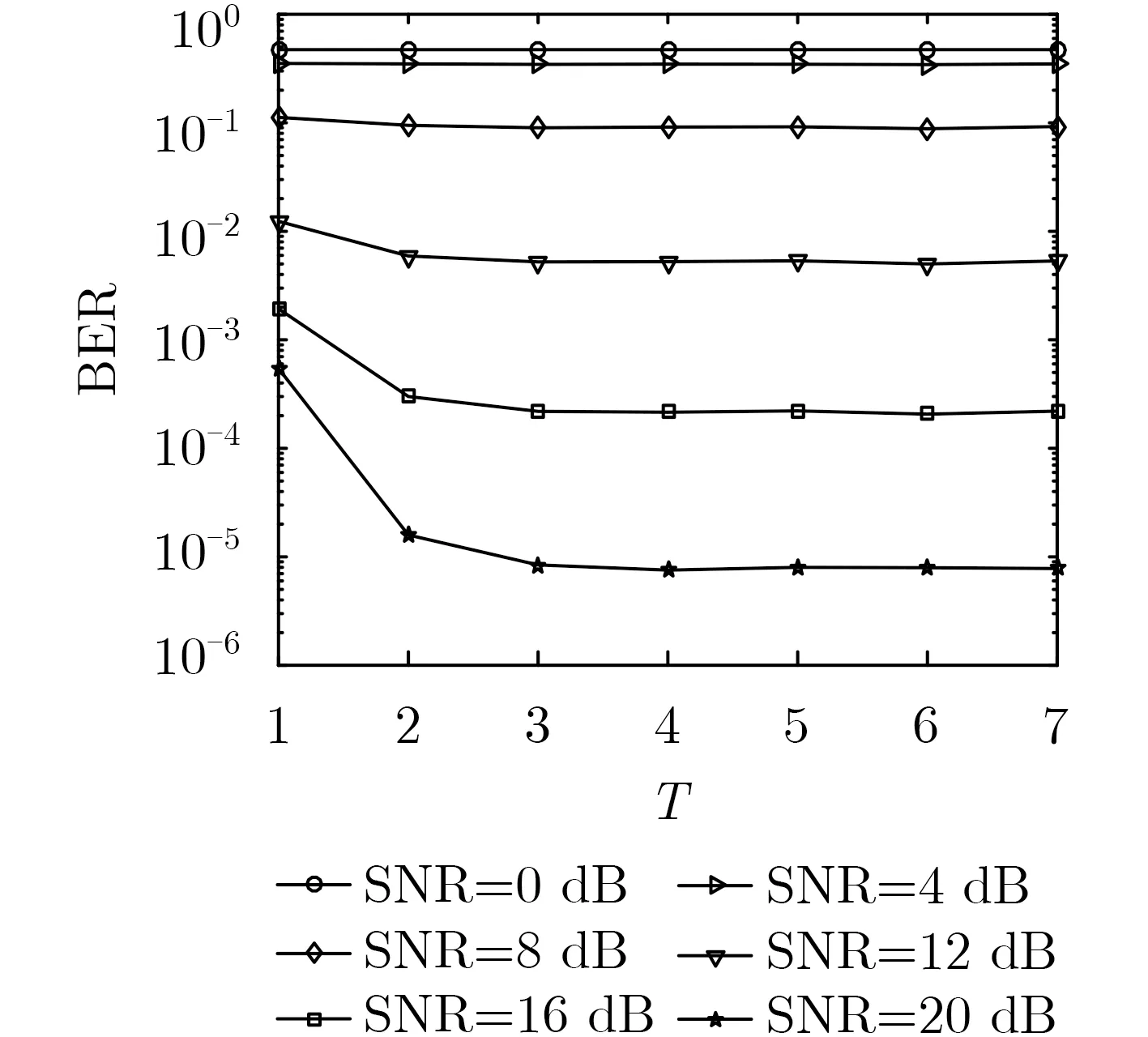
图4 收敛性能曲线图

图5 检测性能随SNR变化的曲线图

当SNR=16 dB, K =16，图6给出CTI, GSI,CG, Neumann及Cholesky算法的BER性能随基站天线数 N 变化的曲线图。受基站天线数 N增加而引起大规模MIMO阵列增益的提升的影响，使CTI算法及其对比算法性能均得到不同程度的改善。然而，在基站天线数相对较少时，CTI算法性能，明显优于Neumann, CG和GSI算法；当基站天线数大于128时，CTI算法可取得接近于Cholesky算法的性能。

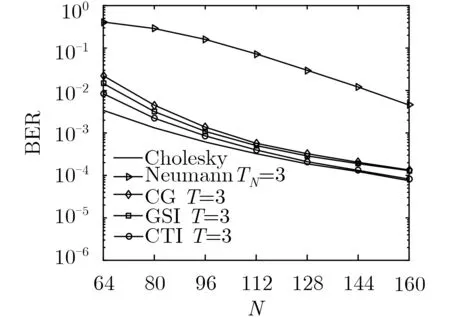
图6 检测性能随基站天线数变化的曲线图

图7在S NR=16 dB, N =128，给出CTI, GSI,CG, Neumann算法以及Cholesky算法BER性能随用户数 K 变化的曲线图。由图7可知，随 K增加，由于用户间干扰逐渐增强，所有检测算法的性能均出现下降。然而，本文所提CTI算法相比Neumann, CG和GSI算法，仍具有一定的性能优势。这说明本文所提算法更适宜用户数相对较多的应用场景。

图7 各算法随用户数变化的性能对比

6 结束语

在大规模MIMO系统中，MMSE算法可取得接近最优的检测性能。但MMSE检测算法涉及高维矩阵求逆运算。同时，当采用HQAM调制时，传统的硬判决检测器很难取得良好的性能。因此，本文基于MMSE框架，提出一种适用于格雷编码的HQAM的大规模MIMO 系统的软输出信号检测算法。在该算法中，通过利用CTI，有效地规避了高维矩阵的求逆运算；同时，利用格雷编码的 22m-QAM信号转化成实数域后的格雷编码的 2m-PAM信号的比特翻转特性，实现了LLR的简化计算。仿真表明，该算法最多3次迭代就可取得接近MMSE算法的性能。然而，需要指出的是，本文所提软输出信号检测算法假设用户配备单根天线，当用户端配置多天线时，发送信号矢量与各用户采取的传输模型(比如空分复用、发射分集等)密切相关，于是，基于CTI算法对信号进行检测时则需要进行相应的调整，针对这些新问题，将在后续研究中深入展开。