家用新能源系统经济运行研究
2021-03-17赵为光赵静强凌泽昊
赵为光,赵静强,杨 莹,凌泽昊
(黑龙江科技大学 电气与控制工程学院,哈尔滨 150022)
0 引 言
家用新能源是光伏发电发展的一个重要方向,太阳能资源分布广泛,家庭能量管理系统为住宅用户提供需求响应,通过减少高峰负荷和将高峰小时需求转移到非高峰时间来降低电力的发电成本,避免不必要的发电,优化了家庭负荷匹配[1-4]。
文献[5]提出了以余电充电比例因子为核心的协调调度策略,得到优化调度方案并进行经济性分析。文献[6]提出了一种实时经济调度方法,依据经济学中边际成本等于边际收益时综合效益最大的原理制定实时经济调度方案。文献[7]计算分布式光伏电站的度电成本和收益,分析了并网电压等级和电量消纳方式对分布式光伏发电成本、收益的影响。文献[8]采用随机机会约束规划建立分布式家庭并网光伏系统优化调度模型。
然而以上文献都没有考虑到多余发电量或者负荷所需的不足电量通过蓄电池和电网的分配比例的问题,也没有考虑到光伏发电能够减少碳排放产生环保收益的问题。该文通过传统与优化家庭光伏发电系统调度策略的对比,针对家庭光伏发电系统的经济调度模型,提出了2个决策变量因子,保证家庭用户的经济收益最大;光伏发电减少二氧化碳的排放,继而减少了除污成本,对环境有一定的保护作用,能够得到环保收益。此文算例以家庭光伏发电系统1天24小时为一个调度周期,建立了经济调度模型,证实该模型的确能提高家庭用户的经济效益,不仅能优化用电结构得到家庭用户最大收益,还能对电网系统进行有效的“削峰填谷”,提高电网稳定性。
1 传统调度策略
现在越来越多的家庭用户响应国家号召,安装了家庭光伏发电系统,该系统大多使用“自发自用,余电上网”模式。该模式是指光伏发电系统产生的电量主要是由用户自己使用,多余电量馈入电网。
家庭光伏发电结构如图1所示,主要由光伏电池,蓄电池和逆变器以及一些负载(如电视,空调、电热水器等)所构成。家庭光伏发电系统将户用光伏系统与电网相连。白天在太阳光的照射下,光伏阵列产生的直流电流通过智能汇流箱,一部分对蓄电池进行充电,一部分传送到逆变器转化为交流电,供给家庭负荷,剩余部分接入电网运行;当阳光不足时,蓄电池向逆变器送电,经逆变器转化为交流电供家庭负荷使用,若蓄电池电量不足,此时需要电网对负荷供电。

图1 家用新能源系统结构图Fig.1 Structure diagram of family new energy system
常见的电价政策为峰谷分时电价,一般蓄电池在峰时段放电,谷时段充电。这样的蓄电池充放电策略存在有很大的限制性。若峰时段的光伏发电量大于负荷所需电量,则此时有剩余电量,该部分剩余电量应该存入蓄电池,即对蓄电池充电,与上述蓄电池在峰时段放电相矛盾。
这种传统策略的实施有很大的随机性和波动性,光伏阵列不具备调度自动化的功能,加大了电网控制与调度运行的难度,容易导致蓄电池组过充、过放,无法充分发挥蓄电池的循环次数,减少它的使用寿命,进而增加光伏发电系统的成本,则本策略不适用。
2 优化调度模型
为了解决传统调度策略的局限性,考虑了光伏政策收入、售电收益、买电成本、系统的维护成本和蓄电池的折损费用5种因素,给出了家用光伏发电系统储能经济优化调度模型,优化光伏发电量大于负荷的售电比例和光伏发电量小于负荷的买电比例。
2.1 决策变量
家庭光伏发电系统产生的电量首先满足家庭负荷,若光伏发电量大于负荷用电量,剩余的电量才会提供给蓄电池和电网;若光伏发电量小于负荷用电量,电量不足的部分由蓄电池和电网提供给家庭负荷。该文提出了2个决策变量因子(售电比例ω(t)和买电比例λ(t))在该系统中协作,ω(t)分配剩余电量并入电网的比例,λ(t)分配电量不足的部分由蓄电池和电网提供的比例。
2.2 光伏电池模型
光伏电池与辐射强度以及温度有关,通过预测每天的太阳辐照强度,就可以估算出其产生的最大功率,光伏发电功率输出为
式中:Ppv为光伏电池的输出有功功率;fpv为光伏发电单元的功率因数;Ypv为光伏阵列的额定容量;GT为实际环境下太阳辐照强度;GTS为标准测试条件下的太阳辐照强度;αp为光伏电池板的功率温度系数;TCS为光伏电池的温度;TC为当前光伏电池的温度,为了便于计算,不考虑电池温度的影响,在有光照时近似取47 ℃。
2.3 储能蓄电池模型
蓄电池荷电状态(State of Charge,SOC)是指电池使用一段时间后剩余电量Eremain与未使用前的蓄电池容量Enominal的比值,按照百分比表示蓄电池荷电状态,其数学模型为[9]
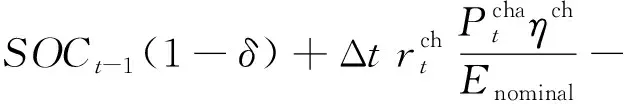

2.4 目标函数
1)能量优化调度的时间为1天24 h,以分配售电比例ω(t)和买电比例λ(t)为优化的决策变量因子,最终实现家庭用户的最大化收益。家庭用户在峰谷分时电价的政策下的收入为光伏政策补贴和售电收益,支出为买电成本、系统的运行维护成本和蓄电池的折旧成本,优化目标函数为
式中:C为家庭光伏发电系统在1天内的最终收益,将调度周期(1天)按小时划分为T个阶段;Csub(t)为家庭光伏发电系统在t时段的光伏政策收入;Csell(t)为家庭光伏发电系统并网卖电收入;Cbut(t)为家庭用户买电费用支出;COM(t)为光伏电池和蓄电池的运行维护支出;Ccost,bat(t)为蓄电池的折旧支出;Pbuy(t)和Psell(t)为t时段家庭用户从电网的购电量和卖入电网的售电量;C0为家庭用户并网售电价格;Cprice为系统从电网的购电价格;PL(t)为t时段家庭负荷的用电量;ω(t)为家庭光伏发电量供给负荷以后多余的电量出售给电网的比例;λ(t)为家庭光伏发电量供给负荷不足的部分从电网购买的比例;k1和k2为光伏电池和蓄电池的运行维护成本支出系数;nB为调度周期内蓄电池总充放电转换次数;Fscost为蓄电池一次转换的折损费用;FB为蓄电池的更换成本;CB为蓄电池标况下额定充放电次数;F为光伏政策补贴。
2)光发电系统在运行过程中没有废气排放,不会对当地环境空气质量产生污染,是最清洁的能源之一。在建造光伏发电系统的过程中会损耗能量产生二氧化碳,所以应该减去制造过程产生的二氧化碳2 525 kW·h,则环保收益为
CP=α(HtPpvPR·N-2525)EI
式中:CP为环保收益;α为二氧化碳折算系数,也可以叫除污成本;Ht为每年的峰值日照时数;Ppv为光伏系统功率;PR为系统综合效率;N为寿命周期年数;EI为二氧化碳排放指数。
传统的发电厂通过化石燃料如煤产生电能,同时产生对环境造成污染的气体,产生的主要是CO2,需要对产生的污染气体进行除污才能将合格的气体排出,因此传统的发电厂会存在除污成本。然而光伏发电不会产生CO2,因此该环保收益就是节省的除污成本。
2.5 约束条件
2.5.1 荷电状态约束
考虑到使用蓄电池期间的维护保养,延长蓄电池的使用寿命,因此要对蓄电池的储能电量和充放电功率进行约束。
SOCmin≤SOC≤SOCmax
上式防止了蓄电池过充和过放。为保证蓄电池的使用年限,规定蓄电池的荷电状态为20%~90%,即SOCmin=0.2,SOCmax=0.9。
2.5.2 储能充放电功率约束
蓄电池深度充放电会影响其使用年限,所以蓄电池的充电功率和放电功率不能超过其额定容量的20%,即
式中:E=20 kW·h,为蓄电池的额定容量;Δt为1 h。
2.5.3 分配比例约束
决策变量因子ω(t)和λ(t)是应该优化的变量,ω(t)分配光伏发电量供给负荷后的剩余电量、λ(t)分配光伏发电量供给负荷的不足电量,二者的约束范围为
2.5.4 系统调度约束
当家庭光伏发电系统的发电量大于家庭负荷的用电量时,剩余光伏发电量部分就按照决策变量因子ω(t)对其进行优化调度,约束为
Psell(t)=[Ppv(t)-PL(t)]ω(t)
Pcha(t)=[Ppv(t)-PL(t)][1-ω(t)]
当家用新能源系统的发电量小于家庭负荷的用电量时,由决策变量因子λ(t)进行优化调度,约束为
Pbuy(t)=[PL(t)-Ppv(t)]λ(t)
Pdis(t)=[PL(t)-Ppv(t)][1-λ(t)]
2.5.5 功率供需平衡约束
家用新能源系统应满足以下功率平衡式,约束条件为
PL(t)=Ppv(t)+Pbuy(t)+
Pdis(t)-Psell(t)-Pcha(t)
当Ppv(t)>PL(t)时,就不需要从电网买电或者通过蓄电池放电了,即Pbuy(t)=0和Pdis(t)=0,约束条件为
PL(t)=Ppv(t)-Psell(t)-Pcha(t)
当Ppv(t) PL(t)=Ppv(t)+Pbuy(t)+Pdis(t) 遗传算法不需要推导和附加信息,寻优规则具有非确定性、自组织、自适应和自学习性等特点,所以本算例中使用遗传算法对目标函数进行寻优,运算流程如图2所示。 图2 遗传算法流程图Fig.2 Flow chart of genetic algorithm 以某一家庭光伏发电用户在1天24 h所需的负荷为例进行分析。该家庭的光伏总装机容量为8 kW,蓄电池的额定容量为20 kW。算例采用峰谷分时电价,峰时段(8∶00-22∶00)电价为0.58元/(kW·h),谷时段(22∶00-8∶00)电价为0.32元/(kW·h)。该地针对光伏发电国家补贴和当地补贴一共0.63元/(kW·h)。该地区脱硫燃煤标杆上网电价为0.3597元/(kW·h)。表1和表2为家庭光伏调度周期内可间断用电负荷和基本用电负荷的基本数据,表3为调度周期内的太阳辐射强度,图3为家庭用户所需负荷曲线和光伏发电量曲线。 表1 可间断用电负荷Table 1 Interruptible electricity load 表2 基本用电负荷Table 2 Essential electricity load 表3 调度周期内的太阳辐射强度Table 3 Solar radiation intensity in dispatching period 从图3可以看出,家庭光伏发电系统的发电量主要集中在调度期的中间时刻,此时光伏发电量大于负荷用电量。家庭用户的日负荷用电量在2个峰谷时段,上午和晚上为峰时段。 图3 家庭用户所需负荷和光伏发电量Fig.3 Load required by family users and photovoltaic power generation 通过遗传算法对该优化调度模型进行求解,主要参数包括初始化种群数目为NP=50,染色体二进制编码长度为L=20,最大进化代数为G=100,交叉概率pc=0.8以及变异概率pm=0.1。调度周期为1天24个小时,根据调度模型和约束条件,通过Matlab仿真寻优,得到图4分配比例因子ω的优化曲线和图5分配比例因子λ的优化曲线。图6为优化调度策略下的经济方案。 图4 ω的优化曲线Fig.4 Optimization curve of ω 从图3~5可以看出,0∶00-8∶00主要是比例因子λ起决定性作用,此时家庭负荷不足的电量需要从电网中获得或者通过蓄电池放电满足日常需求。0∶00-8∶00为谷时段电价0.32元/(kW·h),此时应该从电网中买入电量给负荷供电。9∶00-19∶00主要是比例因子ω起决定性作用,此时家庭光伏发电量大于家庭负荷所需的电量,除了提供给家庭日负荷以外盈余的部分需要卖给电网或者对蓄电池充电。从图5可以看出,9∶00-19∶00盈余的电量大部分都卖给了电网,少部分对蓄电池进行充电,用来维持晚上光伏发电不足时,蓄电池可以供应家庭负荷。20∶00-22∶00时为峰时段电价0.58元/(kW·h),电价较高,此时应该由蓄电池放电供给家庭负荷,避免从电网中买入较高的电价。23∶00-24∶00主要是比例因子λ起决定性作用,光伏发电量为0,家庭负荷也比较少,且此时购买电价为0.32元/(kW·h),则优先从电网中购买电量提供给负荷。0∶00-8∶00为谷时段,此时的电价也比较低,该系统从电网中买电能节省电费开支,在一定程度上能够“填谷”;9∶00-19∶00是用电高峰期,该系统不从电网中获取电量,不增加电网的负担,还能供给电网,缓解了电网的压力,在一定程度上达到了“削峰”的目的。 图5 λ的优化曲线Fig.5 Optimization curve of λ 图6 优化调度策略下的经济方案Fig.6 The economic scheme under optimized dispatching strategy 根据第1.1节的传统调度策略,得到图7传统调度策略下的经济方案。从图7可以看出,14∶00-18∶00有多余电量卖给电网,其余时间都是蓄电池充放电以保证家庭负荷的需求。蓄电池充放电次数过多,对蓄电池的损耗也比较大。在用电高峰期,大部分光伏发电量都存入了蓄电池,用电低谷期,大部分时段都是蓄电池供电,也不利于“削峰填谷”。 图7 传统调度策略下的经济方案Fig.7 The economic scheme under traditional dispatching strategy 通过优化调度策略和传统调度策略的对比,很容易发现,优化调度策略能够改良家庭用户用电的方式,有效地对电网进行削峰填谷,不仅使用户收益达到了最大化,还有效地缓解了电网的压力。表4为2种调度策略下的经济效益对比。 表4 两种调度模式的收益对比Table 4 Revenue comparison of two dispatching modes 光伏发电是值得大力推广的清洁能源,家庭光伏发电系统有效地减少了CO2的排放,节省了除污成本,节约了对环境保护的成本,环保收益为37.156元。 在峰谷电价的基础上,对家庭光伏发电系统的储能经济调度模型进行了研究,引入售电比例ω和买电比例λ这2个决策变量比例因子,通过合理分配售电和买电的比例,利用遗传算法对模型进行寻优求解。结果表明,所研究家庭用户的优化调度比传统调度得到的收益更多,能够节约家庭开支;优化了用电结构,能够在峰时段供给电网,在谷时段大量减少电网电量,减轻了电网的压力,提高了电网的供电可靠性,验证了该优化研究的正确性。2.6 优化调度算法

3 算例分析
3.1 算例数据
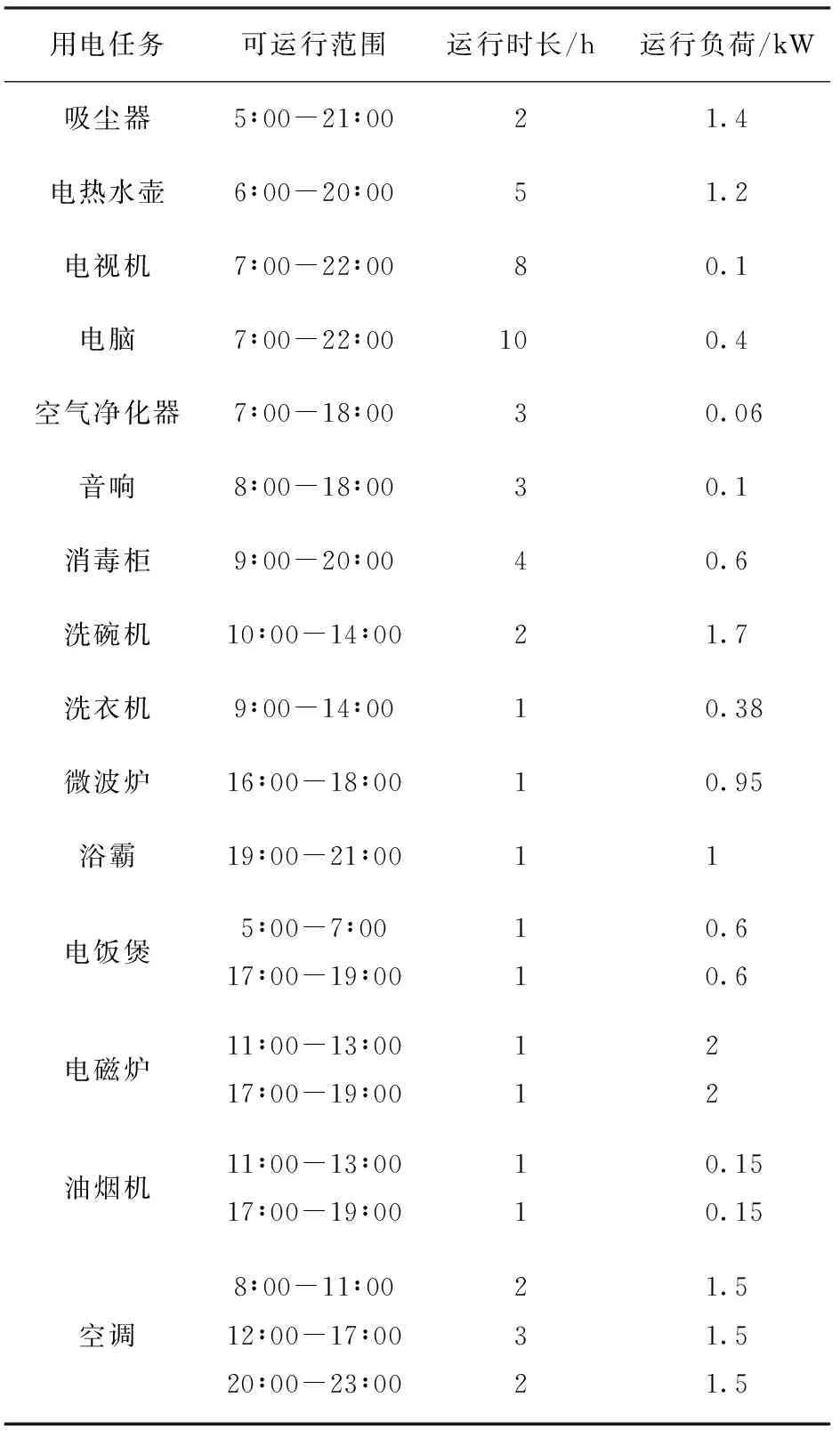



3.2 结果分析



4 结 语
