基于双二阶广义积分器的DFIG次同步振荡抑制策略
2021-03-17祖光鑫武国良张雄鑫李国强张美伦刘智洋
祖光鑫,武国良,张雄鑫,李国强,张美伦,刘智洋,郑 君
(1.国网黑龙省电力有限公司电力科学研究院,哈尔滨150030;2.哈尔滨工业大学,哈尔滨150001)
0 引 言
通常风电场都建设在偏远地区,因此将风能通过机电转换后,需要较远距离的电能输送,才能将新能源电力输出至负荷[1-3]。现代电网中常在线路中采用串补电容的方式降低电感效应的影响,从而提高输电线路的功率因数。串补电容的方法往往会使得电网产生低于电网频率的低频振荡[4-5]或次同步振荡[6-7]。
次同步振荡能量转换的输入与输出形式分为三类,其中次同步控制相互作用(sub-synchronous control interaction, SSCI)是由新能源发电系统的变流器与线路中的串补电容耦合振荡引起的。采用串补电容的双馈感应电机(Doubly Fed Induction Generator,DFIG)电系统如图1所示,这是随着风电渗透率逐步提高引起的电力系统中一种次同步振荡现象。SSCI的产生和传递与机械轴系没有关联,在输电线路中的发散速度更快,对于电网系统的危害更大。
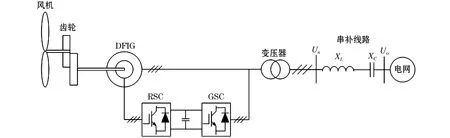
图1 采用串补电容的DFIG电系统Fig.1 DFIG electric system with series compensation capacitor
当线路发生次同步振荡时,电压中的谐波分量会在DFIG的定子中产生相应频率的谐振电流。谐振电流同样也会对转子电流产生影响。该谐振电流分量使得转子电流再次发生畸变。转子侧变流器(Rotor side converter,RSC)检测到含有谐振分量的畸变电流,通过电流反馈及闭环调节调整转子电压产生,进而使DFIG的转子电压中产生谐振分量,由此电压分量会再次产生转子谐振电流分量,周而复始循环造成系统振荡。
文献[8]采用补偿阻尼改进系统的控制策略进而抑制特定频率下的振荡。文献[9]分析了DFIG导致SSCI的原因。文献[10]分析了DFIG内部及外部参数对次同步振荡产生影响。
1 DFIG的数学模型
DFIG转子侧的双PWM变流器中,RSC的主要控制目标是控制DFIG系统的整体输出功率,使DFIG能够运行于最大风能跟踪模式。RSC通常采用定子磁链定向或电网电压定向。当采用电网电压定向的矢量控制,忽略定子电阻Rs,DFIG的定子电压为
us=Rsis+jω1Ψs≈jω1Ψs
(1)
式中:us、is、Rs、Ψs分别为定子侧电压、电流、电阻、磁链,ω1为电网电压角速度。
于是电网电压定向的前提下有
(2)
式中:us,d、us,q为定子电压的d、q轴分量,Ψs,d、Ψs,q为定子磁链的d、q轴分量,Us为定子侧电压幅值。
DFIG定子侧输出的有功及无功功率表达式如(3)所示:
(3)
式中:Ps,out、Qs,out分别为定子侧输出的有功和无功分量,ir,d、ir,q为转子电流的d、q轴分量,Lm为定转子绕组间互感,Ls为定子绕组自感。
由式(2)和式(3)可知,DFIG通过前馈补偿后,其定子侧输出的有功及无功功率已经近似解耦。DFIG转子侧d轴及q轴的电压方程如下:
(4)

转子磁链可表示为
(5)
将(5)代入(4)可得
(6)
2 次同步振荡下的锁相技术
图2是传统的数字PLL的控制框图。PLL通过在d、q坐标系下构建闭环,使得Vq=0,此时电网电压矢量与PLL对于电网电压矢量估计值相等,即锁相成功[11]。

图2 传统锁相环控制框图Fig.2 Control block diagram of traditional PLL
通常认为理想电网电压的表达式如(7)所示:
(7)
通过Clark变换可得到
(8)
通过Park变换可以得到
(9)
将式(9)代入式(8)可得
(10)
式中:ω0为锁相环对于电网角速度的估计,φ0为电网电压矢量与锁相对于电网电压环矢量的估计二者之间的相角差。
(11)
其中:
(12)
进行Clark变换后,有
Vαβ=[VαVβ]T=[Tαβ]Vabc
(13)
其中可知
(14)
在两相静止坐标系下电压正序分量的表现形式如下:

[Tαβ][T+][Tαβ]-1Vαβ=
(15)

由(15)不难发现,要想在两相静止坐标系下对次同步工况的电压中提取出正序分量,就需要将输入信号偏移90°。图3为双二阶广义积分器的控制框图。

图3 双二阶广义积分器控制框图Fig.3 Control block diagram of biquadratic generalized integrator
通过图3双二阶广义积分器的控制框图,能够获得其传递函数如式(16)及(17)所示:
(16)
(17)
做完实验后,学生进行分组汇报。其余小组汇报的时候,有的小组也还在弄自己的东西,教师也没有过多地批评和干涉。结束后,每个小组收拾好自己的实验材料交给教师,教师进行拓展和小结后,科学课就这样结束了,有的学生感觉很有意思,个别学生觉得无聊。不知道是内容太简单还是不喜欢这样的一种教学方式,科学课是否真的点燃学生的探究激情,也还真的值得研究。

图4 双二阶广义积分器的锁相环控制框图Fig.4 Control block diagram of PLL with biquadratic generalized integrator
当DFIG并入的电网发生次同步振荡时,设置电网电压中具有10 Hz的谐波分量,具体的仿真电压波形见图5(a)。图5(b)所示为常规PLL,PLL的电压频率和幅值均有低频扰动分量。图5(c)所示为改进的双二阶广义积分器的锁相环很好地解决了次同步振荡的问题。

图5 次同步振荡下的仿真波形Fig.5 Simulation waveforms under sub-synchronous oscillation
3 基于次同步振荡抑制的转子变流器谐振控制
3.1 转子变流器谐振控制策略
将RSC数学模型进行变换可以得到
(18)
(19)
电流矢量闭环控制框图如图6所示。
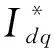
由图6控制框图可得输出电流与指令电流传函为

图6 阻感性负载电流闭环Fig.6 Closed loop of resistance-inductance load current
(20)
可以得到其误差传递函数为
(21)
由式(21)及式(22)得到,当控制器增益|G(s)|≥1时,有|G(s)GP(s)|≥1,可得|F(s)|≈1且|E(s)|≈0。因此在某频率下如果|G(s)|≥1,则谐振控制器可以在该频率下实现无静差控制。举一个例子,如果期望抑制频率为40 Hz的次同步电流分量,图6中
(22)
式中:Kr为增益系数,ωc为截止频率,ωsub为次同步振荡频率。
在针对DFIG次同步振荡抑制的控制中采用基于直接谐振控制的定子电流次同步分量抑制策略。图7为RSC直接谐振控制器的控制框图。
如图7所示,通过PI调节器及谐振控制器二者协调控制,共同输出相减后由电流定向而决定。由式(18)可知,RSC控制器调节输出的参考电压指令矢量形式可表示为

图7 转子侧变流器直接谐振控制Fig.7 Direct resonance control of rotor side converter
(23)

3.2 转子变流器谐振控制性能仿真分析
对次同步振荡影响下的DFIG进行仿真如图7所示。首先在0.4 s在电网电压中加入次同步振荡分量,0.6 s时通过在转子侧变流器中增加谐振控制器环节以抑制次同步振荡。
根据仿真结果(图8)次同步振荡下DFIG定子电流仿真曲线,当DFIG风电系统发生次同步振荡以后,电机定子输出的电流具有明显次同步谐波含量,在0.6 s处加入谐振控制环节之后,次同步谐波电流含量明显减小。
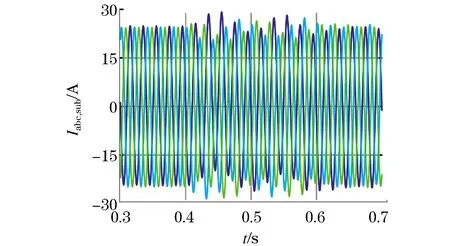
图8 DFIG定子电流Fig.8 Current of DFIG stator
图9为定子单相电压与电流曲线图,通过仿真结果可以看到,在改进控制策略中加入谐振控制环节以后,这种改进使得DFIG风电系统对次同步电压分量的抗扰动能力增强。

图9 定子单相电压与电流曲线Fig.9 Single-phase voltage and current of stator
4 结 语
在建立了DFIG系统数学模型的基础上,对理想电网电压条件下DFIG的数学模型进行了分析。对现代风电场远距离输电中配置串补电容会导致风电场的DFIG机组发生次同步振荡的影响进行了分析,分别考虑了次同步振荡对锁相环及转子侧变流器畸变电压的影响。在此基础上提出了相应的次同步振荡抑制策略,并通过仿真与物理模拟实验验证了所提控制策略的可行性与有效性。
