基于功率的电量智能修复算法研究
2020-12-28于海洋
梅 迪,蒋 蕾,于海洋,禹 加
(国网辽宁省电力有限公司发展策划部,辽宁 沈阳 110000)
0 引 言
受数据采集终端和传输通道等影响,目前营销部门用电信息采集系统的采集成功率仅为60%左右[1]。晚上24点开始采集数据,会导致数据的准确性和实时性较低,实时准确的电力数据才能真正满足电力和经济关系的分析需求,实现电力看经济的目标[2]。本文通过运用异常电量智能修复算法,为行业、公司以及国家等提供真实可用的电量数据。
1 用户电量异常
用户电量通过表底和倍率计算,因此电量异常包含表底异常和倍率异常两种。其中,表底异常包括表底缺失和表底突变。表底缺失是指营销专业用电信息采集系统获取到的表底数值为空[3]。表底突变是指营销专业用电信息采集系统获取到的表底数值较大,计算得出的用户电量超过该用户电量阈值。倍率异常指电能表本身的综合倍率数值异常。综合倍率是电压互感器倍率和电流互感器倍率的乘积[4]。如果营销专业用电信息采集系统获取到的电表倍率为空,那么计算的用户电量为空,则为电量缺失,如果计算的用户电量超过该用户电量阈值,则为电量突变。
2 数据补全方法
对用户的异常电量需要进行数据补全。本文介绍的数据补全方法包含平均值法、基于电量的周期均值法以及功率预测法[5]。
2.1 平均值法
平均值法是一种相对简单快速的计算方法。若某一天的电量诊断为异常,则采取前一段时间电量的平均值作为当天的电量。公式如下:

式中,Ei+1为用户第i+1天的电量,Ei为用户每天的电量,电量的单位为kW·h。n为参与平均电量计算的天数,本文取10天。由式(1)可看出,若用户某天电量异常,则采用该日期往前推10天的电量求和取平均值作为该天电量。该算法简单易懂,但由于没有考虑周末对电量的影响因素,因此数据的准确度不高。若前几天的电量均为修正值,则会大大降低当天数据准确度。
2.2 周期均值法
周期均值法是指在缺失电量的当天向前推1周、2周、3周等,然后取平均值。公式如下:

式中,Et为当天修正后的电量,Ei当天往前推整周的电量,i=t-7、t-14、t-21…,n为参与平均电量计算的个数,本文取3。即i=t-7、t-14、t-21。
由式(2)可以看出,周期均值法在计算缺失日电量时,避免了周末因素,算法简单易懂,缺点是周期较长和样本较少。当样本选取较多时,周期较长,用户用电规律可能发生变化,导致预测电量准确度降低。
2.3 功率预测法
电量的定义为功率数据在时间轴上的积分,也就是说电量是由功率计算出来的。通过历史功率数据和电量数据预测当日电量值,使得预测电量数据准确度更高,更可靠。利用这种方法预测时,需要获取每天0:00~16:00的功率数据曲线,然后计算每天的平均功率,剔除功率不可用数据。平均功率的计算公式如下:

式中,P平均为每天0:00~16:00的平均功率,Pi为每天0:00~16:00每个时刻的功率数据,1小时代表1个点,,功率的单位为kW。n为实际参与计算平均功率的点数。
2.3.1 计算电量增长系数k
(1)若T-0和T-2日有功率和电量数据,则采用下列公式计算电量增长系数:

式中,P平均T-0为预测当日T-0日平均功率数据,P平均T-2为预测当日往前推两日T-2的平均功率数据功率单位为kW。
(2)若T-0和T-2日无功率或电量数据,则往前推1周、2周、3周等查找既有功率又有电量的日期,采用前几周的数据求取电量增长系数。计算公式如下:
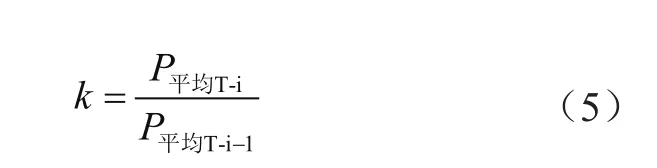
式中,P平均T-i为预测当日往前推1周、2周、3周直至有负荷和电量周的平均功率数据,P平均T-i-1为预测当日往前推1周、2周、3周直至有负荷及电量周的前一日的平均功率数据,i=7、14、21等,平均功率的单位为kW。
2.3.2 预测当天电量数据
(1)若T-0和T-2日有功率和电量数据,则用下列公式计算当日电量:

式中,ET-0为当日预测电量,ET-2为T-2日已计算出的电量,k为电量增长系数。
(2)若T-0和T-2日无功率或电量数据,则用下列公式计算当日电量:

式中,ET-0为当日预测电量,ET-i-1为T-i-1日已计算出的电量。
功率预测法同时考虑了功率、电量以及周期因素。若存在功率和电量,则可直接进行预测,若功率或电量不全,则按周期(剔除周末影响)寻找功率和电量较全的日期,算出电量增长系数,再进行电量预测。这样既避免了平均值法的反复修正,又消纳了周末影响,且数据周期不长,避免用户用电性质发生变化,从而提高用户电量预测的准确性。
3 算例分析
以辽宁省3个典型用户为例,用户1是沈阳桃李面包有限公司,用户2是沈阳浑南矿业有限责任公司,用户3是沈阳礼拜天食品有限责任公司,预测电量时间为2020年7月31日。为验证功率预测法的优越性,选取的3个典型用户该日的电量齐全,未发生异常。如果当天用户电量异常,则分别采用平均值法、周期均值法以及功率预测法修正用户电量,并将修正后的电量与用户真实电量进行偏差比较,验证功率预测法的合理性和准确性。典型用户在7月份10号到31号的日电量如表1所示,7月29日典型用户功率数据如表2所示,7月31日典型用户功率数据如表3所示。
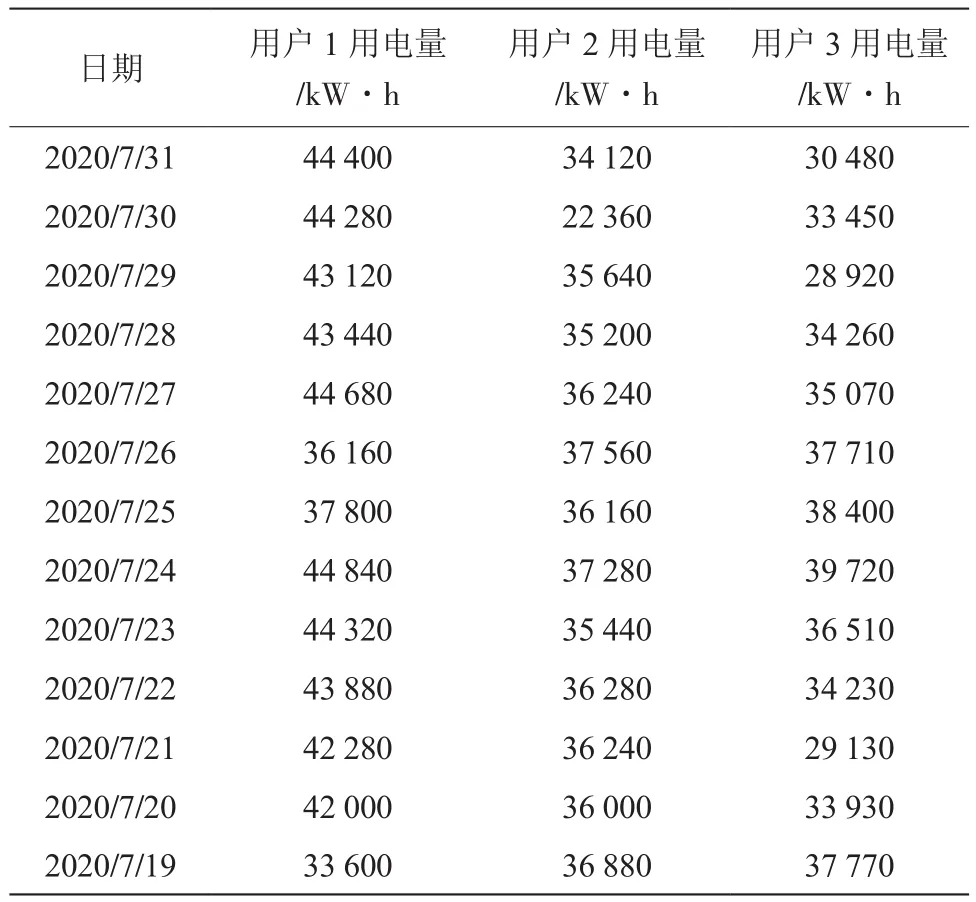
表1 典型用户7月份日电量
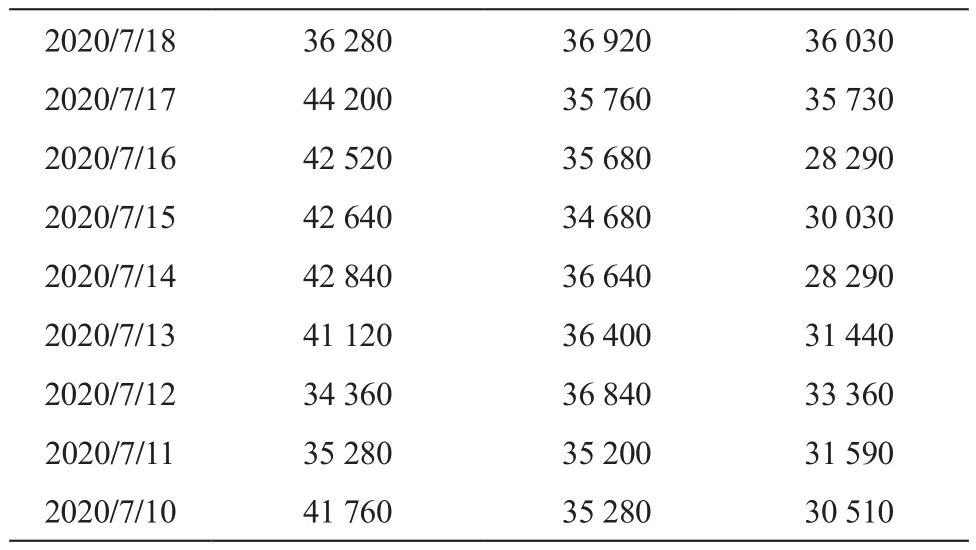
续表1

表2 7月29日典型用户功率数据

表3 7月31日典型用户功率数据
根据以上3种数据补全方法分别进行数据修正,得到修正结果如表4所示。根据表4的修正结果可以看出,平均值法和周期均值法的偏差率有高有低,波动较大,最大偏差率达15%左右,准确度较低。而功率预测法是基于功率和实采电量数据进行的预测修复,不受气温和时间等外部因素的影响,偏差率稳定于2%左右,波动较小,准确度较高。验证了功率预测法的合理性和准确性。

表4 修正结果比对
4 结 论
针对用电信息系统表底数据一次采集成功率较低,售电量分析对电量数据实时性要求较高的现状,本文提出了一种基于功率和电量数据相结合的算法修复异常数据。该算法不受季节、时间以及周期等影响,准确度较高,通过算例计算分析,验证了功率预测法的优越性,促使电量数据归真。
