基于改进BP神经网络的光伏发电预测模型
2021-03-17何家裕吴杰康杨金文余方明梁继深
何家裕,吴杰康,杨金文,余方明,庄 仲,梁继深
(广东工业大学 自动化学院, 广州 510006)
0 引 言
随着经济的高速发展,化石燃料和其他不可再生的自然资源走向枯竭,全球生态环境不断恶化,我国能源的供应和需求间的问题日益突出[1]。作为世界最大的能源消费国和二氧化碳排放国,开展节能发电调度,建立一个最大化利用可再生能源和其他清洁能源,以减少不可再生能源的消耗和污染物的排放和安全、高效、清洁的电力系统是迫在眉睫的[2]。根据“十二五”规划,中国的可再生能源的发电量迅速增长,特别是风力发电、太阳能光伏发电保持较快的年增长,在世界上连续领先多年[3]。随着光伏发电装机容量的增加,大规模的光伏并网,而太阳能光伏发电存在间歇性和不稳定等问题,为了减少光伏发电对电力系统的影响,提高电力系统运行的可靠性,需要尽可能精确地预测光伏发电系统的发电量。
近年来,许多专家对太阳能光伏发电预测技术进行了研究并获得了不少成果。其中,太阳能光伏发电预测技术主要可以分为统计时间序列方法、物理方法和混合方法。统计时间序列方法高度依赖历史数据,主要的方法包括人工神经网络、支持向量机等;物理方法主要取决于物理状态和大气中的太阳辐射的动态运动之间的相互关系,主要的方法包括数值天气预报、卫星成像等;混合方法是统计时间序列方法和物理方法的任意结合[4]。文献[5]提出了一种ANN-MLP模型用于意大利的里雅斯特GCPV电厂前24小时的太阳辐射强度预测。文献[6]提出了一种ELM-ANN模型用于太阳能发电预测。文献[7]提出了一种LS-SVM模型进行麦地那城的气象的短期预测。文献[8]将小波变换(WT)、模糊ARTMAP(FA)和萤火虫(FF)相结合,进行太阳能光伏发电输出功率的短期预测。文献[9]提出了一种基于WT和深度卷积神经网络(DCNN)预测光伏发电功率的新型混合方法。
为了提高电网的运行可靠性和提高对太阳能资源的利用率,建立了基于最大偏差相似准则的混沌遗传-BP神经网络的光伏发电预测模型。本模型使用最大偏差相似性准则算法和混沌算法优化传统的遗传算法,将优化后的遗传算法对BP模型进行优化。本预测模型与CS-SVM模型、BP模型和GA-BP模型相比,具有更快的计算速度和更高的预测精度。
1 影响光伏发电的气象因素
由于光伏发电输出主要由太阳辐射强度决定,而天气的剧烈变化,云层的流动,风速的波动性和随机性会直接影响到太阳辐射强度的强弱[10-11]。大规模光伏发电并入微电网系统会使系统产生不确定性,从而影响微电网的正常运行。因此,有必要分析天气、风速等气象因素对太阳能光伏发电的影响。以下分析以澳大利亚昆士兰大学的UQCentre太阳能433 kW光伏电站的实时播报系统记录的连续3天天气状况为晴天的光伏发电功率数据以及气象数据为研究对象对实际风速、环境温度、环境湿度和太阳辐射强度对太阳能光伏发电功率的影响进行分析。
1.1 实际太阳辐射强度对太阳能光伏发电的影响
图1表明了太阳能光伏发电功率与实际太阳辐射强度间的关系。可以清晰地看出,实际太阳辐射强度与太阳能光伏发电功率之间是呈正相关的关系,太阳能光伏发电功率与实际太阳能辐射强度的曲线有相同的趋势,光伏发电功率随着太阳辐射强度的变化而变化,因此,证实了太阳能光伏发电功率主要是受太阳能辐射强度的影响。

图1 PV发电功率与太阳能辐射强度关系Fig.1 Relationship between PV power and solar radiation intensity
1.2 环境温度对太阳能光伏发电的影响
图2为环境温度与太阳能光伏发电间的关系图。从图2可以看出,早上随着温度的上升,太阳能光伏发电功率也随之上升,经验所得,通常中午的温度达到当天温度的最高值,此时的太阳能发电功率同样达到最大值,午后随着温度的下降,太阳能光伏发电功率也随之下降,因此,可以得出,环境温度的变化对太阳能发电功率产生影响。

图2 PV发电功率与环境温度关系Fig.2 Relationship between PV power and ambient temperature
1.3 环境湿度对太阳能光伏发电的影响
图3是环境湿度与太阳能光伏发电关系的曲线。从图3可以清楚地看出,环境湿度随着太阳能发电功率的上升随之快速下降,下降到太阳能光伏功率达到最大值后,环境湿度保持不变,而随着发电功率下降到最低点,环境湿度回升到最高点,可以得出,其湿度的变化主要是由于当太阳光照强度的增强,大气中的水汽蒸发,使环境的湿度降低,因此,可以得出,环境湿度的变化对太阳能发电功率产生影响。

图3 PV发电功率与环境湿度关系Fig.3 Relationship between PV power and ambient humidity
1.4 实际风速对太阳能光伏发电的影响
除了上述的3个气象因素,风速也是影响太阳能光伏发电的气象因素之一,如图4所示。从图4可以看出,随着太阳能光伏发电功率的迅速上升,实际风速波动性下降,而随着太阳能光伏发电功率曲线的下降,风速随之回升。可以得出,风速的变化在一定程度上会影响到太阳能光伏发电功率。

图4 PV发电功率与实际风速关系Fig.4 Relationship between PV power and wind speed
2 改进后的BPNN微网光伏功率预测模型
2.1 混沌优化
混沌运动存在于许多自然和人造系统中,到目前为止,混沌定义的概念还没有完全建立起来,其运动是随机的、无序的、复杂的[12]。混沌具有遍历性,即可以在有限区间内进行永不重复、形态复杂的运动[13]。该文使用Logistic方程对初始种群进行混沌优化。Logistic方程为[13]
xn+1=μxn(1-xn)
(1)
式中:μ代表的是控制变量,其值为4时,此刻系统的状态为完全混沌状态;xn的取值在(0,1)之间,但取值不能为混沌变量的3个不动点0.25,0.5,0.75。
2.2 GA-BP算法
遗传算法(GA)是一种基于达尔文的生物进化论而产生的群体随机搜索技术和方法。由于算法是多点搜索,具有较好的全局寻优能力,能处理各类非线性问题,因此被广泛地运用在负荷预测、优化问题等。其主要地步骤包括:选择操作、交叉操作和变异操作。
人工神经网络(ANN)是一种基于生物神经网络的信息处理方法,主要由输入层、隐含层和输出层组成。目前最为广泛使用的ANN模型之一的是BP神经网络模型,但该模型的本质为梯度下降法,其收敛速度相比其他算法较慢,在优化过程中易陷入局部最优。为解决以上问题,结合GA算法,通过GA算法优化BP算法的权值和阈值,大大提升了BP算法的收敛速度。
2.3 最大偏差相似准则
最大偏差相似准则算法(MDSC)可以对曲线进行刻画,此时的曲线需要是同类别的且刻画只能针对曲线之间的形态相似性。这种算法的灵活性非常强,因为其可以自由选择相似度、偏离度等条件,不仅如此,这种算法还可以选择很多种精度对曲线之间的相似程度进行测量[14]。
根据文献[14],MDSC的步骤如下:
设有n个m维的时间序列数据,第i个时间序列数据为Xi=(Xi1,Xi2,…,Xim),Xik(≥0)为第i个时间序列的第k个时间点的数据,i=1,2,…,n;k=1,2,…,m。
设Sij,k为xi和xj对应时间点间的欧式距离,i,j=1,2,…,n,k=1,2,…,m,计算公式如下:
Sij,k=|xik-xjk|
(2)
设Sij,k中有nij个满足条件Sij,k≤λ,则称nij为xi与xj两个时间差的相似点数;设Sij中有mij个满足条件Sij,k<λ,称mij是xi与xj两个时间差的最大连续偏离时点数i,j=1,2,…n,k=1,2,…,m。其中,λ(0≤λ≤1)为预设常数,称为最大偏差,其可以对阈值进行衡量,当Sij,k≤λ时,则认为时间序列点xik和xjk相似,如果满足Sij,k≤λ这个条件,那么则认为两个时间点是相似的,如果不满足就不相似。mij的具体表达式为
(3)
以时间序列xi为对比中心,计算xj与xi之间的nij和mij(i,j=1,2,...,n),如果满足下列两个条件:
1)为预设常数,称为相似度;
2)mij≤m0,其中m0=[β×m],β(0≤β≤1-α)是常数,一般都是预先设定好的,叫做偏离度。
就可以认为两个时间点是相似的,且这两个条件就是最大偏差相似性准则。
2.4 改进后的BP神经网络光伏功率预测流程
为了克服两种算法各自的缺点,发挥两种算法的长处,文中将BP神经网络、遗传算法与最大偏差相似性准则和混沌优化结合,应用神经网络的非线性映射、预测和遗传算法全局优化的能力,以及混沌优化的遍历性,使得网络同时具备学习和进化的能力。基本思想为先用基于最大偏差相似性准则的混沌遗传算法对网络进行训练,找到一个较优解,然后将此最优解对BP神经网络的初始权值和初始阈值进行优化[15-18]。
在应用BP神经网络对光伏发电输出功率进行预测之前,需要对光伏发电历史数据进行归一化处理,采用公式(4)对光伏发电历史数据进行归一化处理:
(4)
式中,xi,k所表示的是负荷值,此时的天数是第i天且时刻为k;xmin,xmax代表的物理意义是光伏发电功率数据最大值和最小值。这样可以使得负荷数据落在[0,1]内,加快神经网络的收敛。
基于最大偏差相似性准则的CGA-BP神经网络模型的步骤如下:
步骤1:初始化BP神经网络。
在此步骤将文中第一部分的4个气象因素(太阳辐射强度、环境温度、环境湿度、实际风速)和时间(时间的设置:时间为8:00,即将输入设置为8;时间为8:15即将输入设置为8.25;时间为8:30即将输入设置为8.5;时间为8:45即将输入设置为8.75,以此类推)作为BP神经网络的输入,输出为太阳能光伏发电功率,隐含层数目根据实际情况进行确定。
步骤2:种群初始化。
在此步骤,根据步骤1的BP神经网络结构进而确定遗传算法个体编码的长度,遗传算法个体编码的长度计算公式为
L=a×b+b×c+b+c
式中:a为输入层节点数;b为隐含层节点数;c为输出层节点数。对种群个体进行实数编码,每个个体的长度均为L。
步骤3:对初始种群进行混沌处理。
在此步骤,根据式(1)产生的随机数生成初始种群,再通过式(5)、(6)将初始种群映射到解空间。
(5)
xi=zi(xi,max-xi,min)+xi,min
(6)
步骤4:计算种群适应度,从中找出最优个体。
此步骤采用式(7)计算种群适应度,并将种群适应度值最小的作为最优个体。
(7)
式中:n为BP神经网络输出节点数;yi为BP神经网络第i个节点的期望输出;oi为第i个节点的预测输出;k为系数。
步骤5:选择操作。本案例中使用轮盘赌法进行选择操作。
步骤6:交叉操作。本案例中使用实数交叉法进行交叉操作。
步骤7:变异操作。
步骤8:对种群的所有个体由式(3)计算个体与全局最优个体间的相似度nij和偏离度mij,并由最大偏差相似性准则判断个体与全局最优个体是否相似,直至遍历种群中所有个体。
步骤9:将与全局最优个体相似的个体进行混沌处理。
步骤10:判断进化是否结束,若否,则返回步骤4。
步骤11:将全局最优个体进行顺序拆分处理,将处理后的个体分别对BP神经网络的初始权值和初始阈值进行优化。
步骤12:对样本进行训练,然后再进行计算得到系统的输出值和真实值之间的差值。
步骤13:如果误差在系统的允许范围之内,进行步骤14;否则,转到步骤12。
步骤14:应用训练后的网络进行预测,将预测结果进行输出。
改进后的BP神经网络算法的流程图如图5所示。

图5 改进后的BP神经网络算法流程图Fig.5 Flow chart of improved BP neural network algorithm
3 算例与分析
3.1 数据来源
以2018年1月1日至1月25日澳大利亚昆士兰大学的UQCentre太阳能433 kW光伏电站的实时播报系统记录的光伏发电功率数据以及气象数据为研究对象,时间选取早上六点到下午六点,时间分辨率为15 min,即每天选取49个时间点。本仿真将时间长度为1 d设置为短期负荷预测,将时间长度为3 d设置为长期负荷预测。为了验证算法的有效性,在Matlab2018b的环境下利用了Matlab自带的神经网络工具箱建立了4种预测模型:
1)布谷鸟算法优化支持向量机算法的太阳能光伏发电预测模型(CS-SVM模型);
2)传统的BP神经网络太阳能光伏发电预测模型(BP模型);
3)遗传算法(GA)优化BP神经网络的太阳能光伏发电预测模型(GA-BP模型);
4)改进后的BP神经网络太阳能光伏发电预测模型(改进后BP模型)。
3.2 参数选择
为降低神经网络的随机性而造成的误差,此文采用试错法[16]对隐含层数目进行确定。首先任意给定参数,接下来的每次选值除了改变隐含层数目,其余参数均保持不变的情况下,通过反复进行30次重复实验,并取其平均值作为所在隐含层数的平均绝对误差百分比(MAPE)。最后可得,当隐含层数目为9时可以使得平均绝对误差百分比最小,结果如图6所示。

图6 隐含层神经元数目与MAPE的关系Fig.6 Relationship between the number of neurons in hidden layer and MAPE
除了隐含层数目的设置外,还有BP算法的参数设置,遗传算法的参数设置如表1所示。此外,将最大偏差相似性准则中的最大偏差α设置为0.1。

表1 BP算法与GA算法参数Table 1 Parameters for BP algorithm and GA algorithm
3.3 预测模型结果评估
根据相关文献,目前对于太阳能光伏预测模型的评估有MSE、MAPE和MAE等方法[15-18],该文选取平均绝对误差百分比(MAPE)和均方误差(MSE)作为模型的评估方法。
3.4 仿真结果与分析
图7~10分别为CS-SVM、BP、GA-BP和改进后BP模型的短期光伏发电功率预测结果。可以看出,CS-SVM模型的预测输出基本偏离期望输出,而在早上6:00到8:00时段,BP模型的预测曲线基本偏离期望输出曲线,而GA-BP模型和改进后BP模型在该时段基本拟合,而在中午12:00到14:00时段,BP模型和GA-BP模型的预测输出曲线明显地偏离期望输出曲线,而改进后的BP模型,全天的预测输出曲线与期望输出预测曲线基本拟合。因此可以得出在这4种模型中,效果最好的为改进后BP模型,其次是GA-BP模型和BP模型,效果最差的为CS-SVM模型。

图7 CS-SVM短期预测输出Fig.7 Short-term prediction output of CS-SVM

图8 BP神经网络短期预测输出Fig.8 Short-term prediction output of BP neural network

图9 GA-BP神经网络短期预测输出Fig.9 Short-term prediction output of GA-BP neural network

图10 改进后的BP神经网络短期预测输出Fig.10 Short-term prediction output of improved BP neural network
图11~14分别为CS-SVM、BP、GA-BP和改进后的BP模型的短期光伏发电预测误差。结合表2可以看出,BP模型和GA-BP模型的预测误差的最大误差绝对值均超过9,CS-SVM模型的最大误差绝对值最高高达18.44,而此文提出的改进后BP模型预测误差绝对值基本维持在2.5以下,说明本模型能准确地对太阳能光伏发电功率进行短期功率预测。
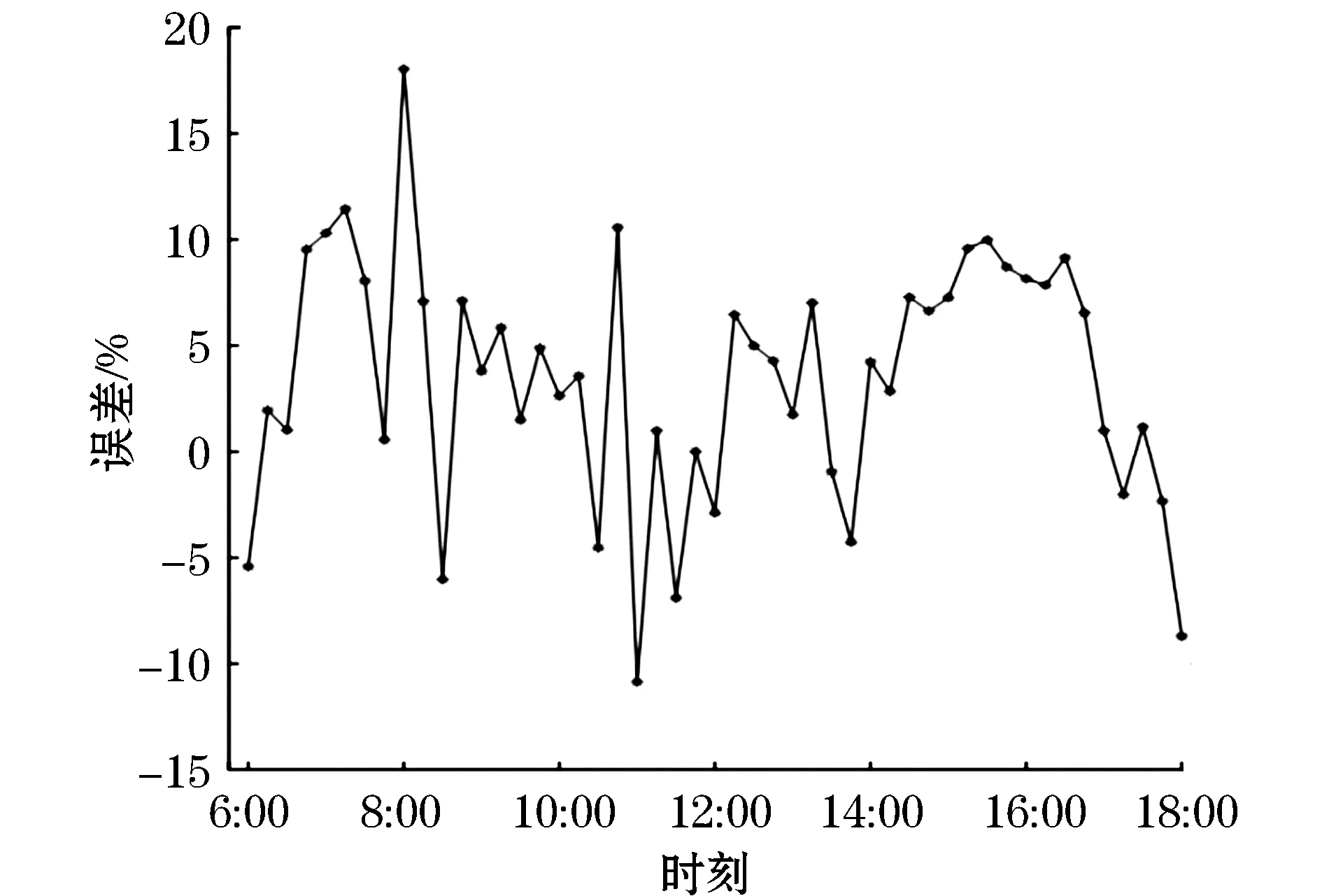
图11 CS-SVM短期预测误差Fig.11 Short-term prediction error of CS-SVM

图12 BP神经网络短期预测误差Fig.12 Short-term prediction error of BP neural network

图13 GA-BP神经网络短期预测误差Fig.13 Short-term prediction error of GA-BP neural network.

图14 改进后的BP神经网络短期预测误差Fig.14 Short-term prediction error of improved BP neural network

表2 不同算法的短期预测结果及误差Table 2 Short-term prediction results and errors based on different algorithms
CS-SVM、BP、GA-BP和改进后BP模型的长期光伏发电功率预测结果分别由图15~18表示。可以看出,CS-SVM模型和BP模型的预测输出曲线和期望输出曲线偏离明显,GA-BP模型和改进后BP模型的预测输出曲线和期望输出曲线基本拟合,但相比于BP模型和GA-BP模型,改进后BP模型预测精度相对较高。

图15 CS-SVM长期预测输出Fig.15 Long-term prediction output of CS-SVM

图16 BP神经网络长期预测输出Fig.16 Long-term prediction output of BP neural network

图17 GA-BP神经网络长期预测输出Fig.17 Long-term prediction outputof GA-BP neural network

图18 改进后的BP神经网络长期预测输出Fig.18 Long-term prediction output of improved BP neural network
CS-SVM、BP、GA-BP和改进后BP模型的长期光伏发电功率预测误差结果分别由图19~22表示。结合表3可以看出,虽然在早上6点到7点时段BP模型的预测精度为最低,但是在全天功率预测时,CS-SVM模型的预测精度波动最大误差绝对值接近9,BP模型的预测精度波动最大误差绝对值接近20,而虽然GA-BP模型的最大误差绝对值最大为4,但其曲线波动较大,而改进后的BP误差曲线基本维持在绝对值为2的范围附近,因此,改进后的BP模型的长期太阳能负荷预测效果优于CS-SVM模型、BP模型和GA-BP模型。

图19 CS-SVM长期预测误差Fig.19 Long-term prediction error of CS-SVM

图20 BP神经网络长期预测误差Fig.20 Long-term prediction error of BP neural network

图21 GA-BP神经网络长期预测误差Fig.21 Long-term prediction error of GA-BP neural network

图22 改进后的BP神经网络长期预测误差Fig.22 Long-term prediction error of improved BP neural network

表3 不同算法的长期预测结果及误差Table 3 Long-termprediction results and errors based on different algorithms
表4为不同模型短期预测误差的对比,表5为不同模型长期预测误差的对比。从表4和表5的平均绝对百分比误差和均方根误差可以看出,BP、GA-BP和改进后BP这3种模型对于光伏发电的预测精度都比较高,其平均绝对误差百分比都在10%以下,而CS-SVM无论是短期太阳能光伏发电功率还是长期太阳能光伏发电功率,效果较差,而提出的改进后BP神经网络的整体预测结果具有较高精度。除此之外还可以看出4种模型的长期光伏发电功率预测精度比短期光伏发电功率预测的精度低,但改进后BP网络的预测精度相比于CS-SVM模型、BP模型和GA-BP模型依具有较高精度。

表4 不同模型短期预测误差对比Table 4 Comparison of short-term prediction errors of different models

表5 不同模型长期预测误差对比Table 5 Comparison of long-term prediction errors of different models
4 结 语
为了提高光伏发电功率预测模型的准确性,提出了一种基于最大偏差相似性准则的混沌遗传-BP神经网络光伏功率预测模型。该模型首先应用混沌优化算法对遗传算法的初始种群进行混沌处理,改善了初始种群的分布特性。其次,采用最大偏差相似性准则对种群进行筛选,将筛选后的种群进行混沌映射,它可以使算法跳出局部最优解,提高算法收敛到全局最优解的可能性。最后,改进的遗传算法用于优化神经网络的初始权重和阈值,以防止神经网络在训练期间陷入局部最优。提出的基于最大偏差相似性准则的混沌遗传-BP神经网络光伏功率预测模型可为光伏发电预测提供参考。
