借助经典模型 模拟试题命制

福建省德化第一中学(362500) 吴志鹏

高考试卷中有许多经典题目,这些题目之所以能够成为“经典”,在于其能够成为后续教与学的好帮手,为后续的教与学起到良好的示范作用,不仅如此,经典的高考试题对于试题的命制也有着很好的启发作用, 为命制试题提供依据,命题教师能够更好地体会经典试题的灵魂与精髓,从中提取模型,熟练掌握命题的原则和技巧,进行试题的命制尝试,本文以2016年全国卷II 文、理科填空题的第12 题为例,谈谈如何借助经典高考试题模拟命制高中数学试题.

一、模拟试题命制的程序

借助经典的高考试题进行试题的模拟命制,首先要对高考试题进行详细的解读,了解其考查的主要知识点和相关知识点,理解其所蕴含的数学思想、方法,以及核心素养;其次要弄清高考试题的命制手法, 为试题命制提供依据和思路,如下文的引例1、2 首先是利用两个中心对称图象的交点来设计和命制试题;其次要对试题进行改造与变式,把对称这个特征融入到相应的函数或问题情境之中,对试题的条件或结论进行变更;最后要对所设计的问题进行验证、完善以保证其科学性与思想性,同时进行难度预测,最终形成符合相关要求的试题.

二、借助经典,提取模型

引例1(2016年高考全国II 卷理科第12 题)已知函数f(x) (x ∈R)满足f(−x) = 2−f(x),若函数y=与y=f(x)图像的交点为(x1,y1),(x2,y2),··· ,(xm,ym), 则=( ).

A.0 B.mC.2mD.4m

解函数f(x)(x ∈R)的图象与函数y=的图象均为中心对称图形,且对称中心均为(0,1),则两图象相应的交点也会关于点(0,1)对称且对称中心不在函数图象上,所以交点必为偶数个, 则m为偶数, 有×0 = 0,0+m=m.

引例2(2016年高考全国II 卷文科第12 题)已知函数f(x)(x ∈R)满足f(x)=f(2−x),若函数y=|x2−2x−3|与y=f(x)图像的交点为(x1,y1),(x2,y2),··· ,(xm,ym),则=( ).

A.0 B.mC.2mD.4m

解因为函数y=f(x) 的图像关于直线x= 1 对称,y=|x2−2x −3|=|(x −1)2−4|, 其图像关于直线x= 1 对称.所以它们图像的交点也关于直线x= 1 对称.当m为偶数时,=m; 当m为奇数时,+1=m.故选B.

对比引例1 和2 的两道试题,不难发现试题均给出两个具有自对称图象的函数,其中引例1 给出了两个具有相同对称中心的函数, 引例2 则给出两个具有相同对称轴的函数,两个函数图象相交,结合交点的对称性,求各个交点横(纵)坐标和,两个试题的命制有着“异曲同工”之妙.学生若能熟练从两类函数(抽象与具体函数)中提取函数图象的对称特征,解决问题也就能够“水到渠成”.同样的,这样的一个经典高考试题也给我们平时的数学试题的命制提供一种可借鉴的模型,即构建“两个具有对称性的函数图象相交,求其交点的横(纵)坐标和”.有了这样的一个数学模型,我们即可动手实施试题的模拟命制.

三、改造模型,命制试题

1 基本函数模型的选择

由于试题缘自于两个具有对称性(中心对称、轴对称)函数的图象的交点,命制试题可选择从基本函数的模型入手.

(1) 具体的函数模型关于原点成中心对称的的一些函数(奇函数)如:f(x) =x,f(x) =x3,f(x) =,f(x) =sinx,f(x)=tanx,关于y轴对称的函数(偶函数)如:f(x)=x2,f(x)=cosx,f(x)=|x|,f(x)=ln|x|,f(x)=e|x|等.

(2) 抽象的函数模型若函数y=f(x)的定义域为R,且满足条件f(a+x) =f(b −x),则函数y=f(x)的图象关于直线x=对称,反之亦然.若函数y=f(x)的定义域为R, 且满足条件:f(a+x)+f(b −x) = 2c, 则函数y=f(x)的图象关于点成中心对称,反之亦然.

2 基本函数模型的改造

对所选取的基本模型进行加工、处理,变换模型的呈现形式,以考查学生直观想象、数学建模、数学抽象、数学运算等核心素养, 通过改造还可以更好地调整试题的难度系数,以使得试题的命制更科学、合理.以下我们通过构造(1,2)为对称中心的函数进行说明.

(1) 直接改造由一些具有对称性的函数图象经过平移、伸缩和对称等变换, 其对称性保持不变这一性质, 所以可通过这样的一种方式对一些具有对称性的基本函数作一定的改造: 将奇函数y=图象向右平移一个单位, 再向上平移两个单位得y=此时, 所给的函数f(x) =的图象便是关于点(1,2)成中心对称.又如选取奇函数y=x3作为基本函数, 通过同样的平移变换则可得函数y= (x −1)3+2 =x3−3x2+3x+1,这样函数f(x) =x3−3x2+3x+1 图象的对称中心也是点(1,2).对于抽象函数, 也可利用平移、伸缩等手段对相关模型进行加工、改造.如函数y=f(x)的定义域为R,且满足f(a+x)+f(b −x) = 2c, 则函数y=f(x) 的图象关于点成中心对称, 反之亦然.我们可作如下改造: 函数y=f(x+1) 关于点(0,2)成中心对称或是函数y=f(x+1)−2 是一个奇函数;或函数y=f(x)的定义域为R,且满足条件:f(1+x)+f(1−x) = 4.这样的改造也是可以获得函数y=f(x)图象关于点(1,2)成中心对称.

(2) 间接改造为使改造后的模型的一种条件更为隐蔽,更好地考查学生的某些方面的核心素养,如运算素养,我们可通过运算公式f(x)+f(2−x)=4 完成模型的改造,如:已知函数为f(x) =此时函数y=f(x)的图象也关于点(1,2)中心对称.

3 搭建特定模型,命制试题

完成基本模型的改造之后,我们必须将改造过的两个函数模型有机地结合在一起、置入背景,融模型于特定的背景之中,搭建出特定的模型,以便更好的对所命制的试题进行科学、合理的呈现,如:

(1) 移植变换构建模型把改造后的基本函数模型移植到经典的高考试题所构建的数学模型之中,这样就能高效地命制出试题.

选取两个具体函数模块进行组合

例1函数y=的图象与函数y=sinπ(x−1)+2(−2 ≤x≤4)的图象所有交点的横坐标之和等于( )

A.2 B.4 C.6 D.8

命题思路本题选择了两个以(1,2)为对称中心的具体函数组合命制试题,考查学生转化函数,奇、偶函数图象的变换,以及利用对称性进行求值等知识.

解函数y=的图象是奇函数y=的图象向右平移1 个单位再向上平移2 个单位得到的, 图象关于点(1,2)对称.函数y= sinπ(x −1)+2 的图象是由函数y= sinπx的图象向右平移1 个单位再向上平移2 个单位得到, 因而函数y= sinπ(x −1) + 2 的图象关于点(1,2) 对称.作草图可知函数y=的图象与函数y= sinπ(x −1)+2(−2 ≤x≤4)的图象交点共有2 对,每一对交点关于点(1,2)成中心对称,横坐标之和为2,故所有交点的横坐标之和等于4.选B.

例2(将一个抽象函数与一个具体函数进行组合)已知函数f(x)(x ∈R)满足f(1−x)+f(1+x)=4,若函数y=与y=f(x) 图像的交点为(x1,y1),(x2,y2),··· ,(xm,ym),则=( ).

A.0 B.mC.2mD.3m

命题思路本题给出了一个有对称中心的抽象函数和一个具有相同对称中心的具体函数,结合交点的对称性求各个交点横坐标与纵坐标的和,若能熟练从两类函数(抽象与具体函数)挖掘图象的对称特征,则可以顺利求解.

解题目所给的抽象函数与具体函数均有对称中心(1,2), 则相应的交点也会关于点(1,2) 对称, 所以×4 = 2m, 则=m+2m=3m.选择D.

例3(对两个抽象函数加以组合)已知函数f(x)(x ∈R)满足f(1−x)+f(1+x) = 4,若函数y=g(x −1)+2 是一个奇函数,函数y=g(x)与y=f(x)图像的交点分别为(x1,y1),(x2,y2),··· ,(xm,ym),则m∑i=1(xi+yi)=( ).

A.0 B.mC.2mD.3m

命题思路本题给出了两个有相同对称中心的抽象函数,求各个交点横坐标与纵坐标的和,若能熟练从两个抽象函数寻找出图象的对称特征,则可顺利求解.(解法同例2,过程从略.)

(2) 逆向变换构建模型把问题的条件和结论进行逆向转换,由果到因,进行思考与命制试题.

例4已知函数f(x) =x3−3x2+ 3x+ 1, 函数y=g(x+ 1) 关于点(0,2) 成中心对称, 若函数f(x) =x3−3x2+3x+1 与y=g(x)图像的交点横坐标和为3,则两个函数图象交点的个数值为( )

A.1 B.2 C.3 D.4

命题思路本题给出了有相同对称中心的一个抽象函数和一个具体函数,通过逆向变换,把两对称函数函数的图象交点的横(纵)坐标值的和,判断两函数图象交点的个数或转化成求函数零点的个数或转化求解方程的根的个数等问题.建构模型即给出交点纵坐标的和,求交点的个数.

解由于三次函数f(x)=ax3+bx2+cx+d(a ̸=0)的图象的对称中心为这点恰为三次函数的拐点(凹凸分界点).本题利用三次函数对称特征构造出对称中心为(1,2)的函数,y=g(x)的对称中心也是(1,2),交点横坐标和为3,说明两函数图象有三个交点,其中对称中心也是两函数图象的一个交点.

(3) 类似变换构建模型通过类比知识内容、迁移解题思路、方法等变换构建相似的模型,命制试题进行考查.

例5已知函数f(x) =x2−2x+ae|x−1|有唯一零点,则a=( ),

命题思路将具有对称中心的函数变换为轴对称函数的进行对称函数模型的构造,并利用其函数图象交点的对称性进行问题的设计、命制试题,利用类似变换,构建模型,命制试题也是教师平时命题常用的一种手法.

解令g(x) =x2−2x,h(x) =ae|x−1|, 则 函 数f(x) =g(x) +h(x).由于函数g(x)、h(x) 的图象均关于直线x=1 成轴对称,因而函数f(x)的图象关于直线x=1对称.又因为函数y=f(x)有唯一零点,所以必有f(1)=0,解得a=1,所以选D.

(4) 弱(强)化条件构建模型加强条件与弱化条件是利用模型命制试题常用的两种方法,通过弱(强)化题目所给的条件增加或降低试题的难度,使它适合不同层次的学生.

例6设函数f(x) = (x −1)2sin(x −1) + 2 在区间[−1,3]上的最大值和最小值分别为M,m,试确定M+m的值.

命题思路把两个具有对称中心的函数的交点改造成为一个有对称中心的函数图象在某个对称区间的最大值与最小值的和,通过弱化条件进行试题的改造,有时也可收到意想不到的效果.

解因为函数f(x) = (x −1)2sin(x −1)+2 的图象可以看作是函数g(x)=x2·sinx的图象向右平移1 个单位,再向上平移2 个单位而得到的,由于g(x)是奇函数,关于原点成中心对称,所以f(x)的图象关于点(1,2)成中心对称,图象的最高点与最低点也关于点(1,2)对称,所以M+m=4.

例7已知函数为f(x)=的值为( )

A.2019 B.2020 C.4039 D.4040

命题思路给定一具有对称中心(1,1)的函数,把两个函数弱化为一个函数,通过对结论的设计,利用对称的性质进行求解计算,通过条件弱化进行试题的改造,所以这些更见教师命制试题的功底和能力.

解因为f(x)+f(2−x) = 2,其图象关于点(1,1)成中心对称,即f(x)+f(2−x)=2,从而有

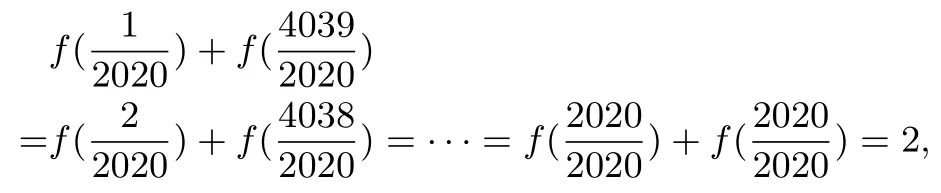
所以

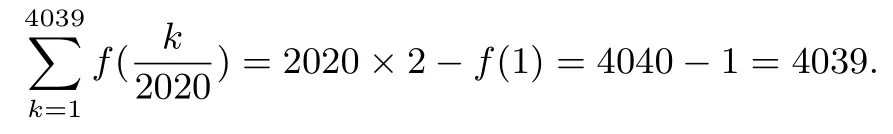
故选C.

四、加强验证,完善试题

科学性和思想性是评价试题命制好坏的一个很重要标准.试题的科学性要求试题合理、完整,经得起“推敲”,做到零失误.在命题过程中,除了要保证文字、符号、标点和图表准确无误之外,更要从不同角度运用逻辑推理的方法进行多次推理、演算,以保证结论的存在性和正确性.尽最大可能地保证试题命制的科学性,杜绝技术性错误的产生.试题思想性则是一道题目是否能够成为经典之作,是否具有一定的启示性,是否成为“好题”的关键.为此,要求命题者要给试题注入数学思想,让数学思想溶解于试题的情境中.如本文所罗列的高考试题和其变式问题,其函数解析式均具有对称的特征,融入了对称的数学思想,而使得试题的意境优美而富有活力.显然借助经典的高考试题是试题命制作的一种手段,也是高效的.试题模拟命制完成之前,可借助学生和同行的解答以保证试题的完整性和科学性,不出现漏洞;也可以借助说题这种教研形式进行试题的深度研究,以达到数学思想性的要求.

试题的命制方法有很多,“经典”的高考试题是教师平时命制试题的“源泉”,充分提取高考试题的模型,通过植入变换、逆向变换、类似变换、数形变换、几何变换、弱(强)化条件等方法进行试题的命制尝试,充分体验高考经典试题的命制手法,灵活模拟试题的命制,应该成为教师教学的一项基本功,也一定会为教师的教育教学带来良好的收益.