基于综合难度系数模型的高考数学试题评价研究
——以2019和2020年高考理科数学全国Ⅱ卷为例
2021-03-17四川师范大学数学科学学院610000徐思迪
四川师范大学数学科学学院(610000) 徐思迪 张 红
一、引言
2014年《国务院关于深化考试招生制度改革的实施意见》的颁布,标志着新一轮考试招生制度改革全面启动[1].随着高考改革的逐步深化,社会各界对教育不断重视,大众对高考也愈发关注.在2019年6月《国务院办公厅关于新时代推进普通高中育人方式改革的指导意见》中强调要深化考试命题改革,提高命题质量,优化考试内容,科学设置试题难度[2].《2019年普通高等学校招生全国统一考试大纲》及《2020年普通高等学校招生全国统一考试大纲》明确提出数学应用问题难度要符合考生的水平,兼顾试题的基础性、综合性和应用性[3].
数学高考难度一直以来是教师、学生、家长关注的焦点,数学高考也是数学课程的重要组成部分,直接反映数学课程的内容,成为教学的导向.同时也是评价学生获得数学知识的指标.数学高考题的质量不但影响着数学课程的质量及水平,而且也是影响数学教育质量的重要因素.因此,对于高考试题的难度分析,有助于优化试卷内容,科学设置试题,提高命题质量;也能帮助一线教师更透彻地分析试卷,明晰高考试卷的变化趋势,提高教学质量.
笔者借助综合难度系数模型以2019 和2020年高考理科数学全国Ⅱ卷为研究对象,通过科学统计和分析,在技术层面对试卷做出较为科学的解析以供参考.
二、综合难度系数模型
综合难度系数模型来源于Nohara(2001)提交给美国国家教育统计中心的工作报告,报告中对NAEP2000、TIMSSR、PISA2000 进行比较, 首次提出了总体难度(Overall difficulty)的概念[4].其中涉及“扩展性问题”、“实际背景”、“运算”、“多步推理”四个难度因素[5].国内学者鲍建生通过对平均难度的不足进行分析.以Nohara(2001)模型作为蓝本,根据我国具体特点进行调整, 保留原模型的“背景”、“运算”、“推理”三个因素,取消“题型”因素,用“知识含量”、“探究”取而代之,在这一模型下各因素的划分如表1 所示[6].
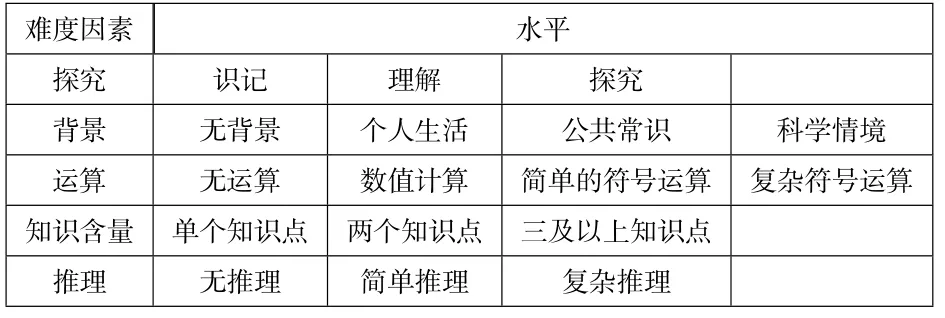
表1:难度因素划分水平)高考文科数学全国卷选填题考查状况分布
为了对每个因素的难度水平进行量化,研究者须对不同难度因素中的不同水平赋予一定的权重系数,对不同的水平由低到高按照1,2,3,4 进行赋值,作为权重.如“知识含量”有三个水平,它们的权重分别为1,2,3,再根据具体情况对试题的各个难度因素进行编码,最后利用下列模型进行计算:
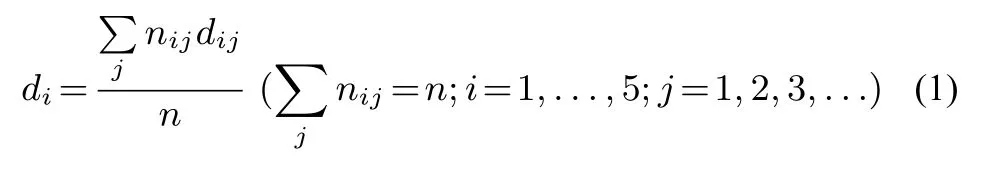
其中,di依次分别表示“探究”“背景”“运算”“知识含量”和“推理”五个难度因素上的取值;dij为第i个难度因素的第j个水平的权重(依水平分别取1,2,3,....) ;nij表示这组题目中属于第i个难度因素的第j个水平的题目的个数,它的总和等于这组题目的总数n[7].根据统计分析结果得到综合难度系数雷达图.
综合难度系数模型是一种利用等级权重来测量和比较难度的研究方法,在教材比较中运用的较为广泛,如鲍建生学者对中英两国初中数学期望课程的难度比较研究,给我国数学课程改革提供有价值的参考建议.朱娅梅利用综合难度系数模型对中美初中数学教材综合难度做比较研究,总结出中国教材可以从美国教材编写中得到的启示.然而综合难度系数模型在试卷难度的比较分析中应用较少,与综合难度系数模型相关的试卷分析有: 张玉环等人运用综合难度模型从国际视野中审视中国高考,并提出新高考的命题建议;邓振江通过综合难度系数模型对2015-2016年数学试题进行分析对2017年的备考提出建议;武小鹏等人根据高考数学试题,对综合难度系数模型进行改进,在原模型中加入思维方式和有无参数,并对各因素的水平按照高考题目做详细的界定和准确的划分,使得模型与高考试卷更加切合.
本研究保留鲍建生的综合难度系数模型中的“推理”、“知识含量”两个因素, 在“运算”因素上, 由于数学试题基本涉及到运算,有数值和符号等不同的运算形式,故将鲍建生提出的“无运算”“数值运算”、“简单符号运算”及“复杂符号运算”四个水平划分为“无运算”、“简单数值运算”、“复杂数值运算”“简单符号运算”“复杂符号运算”五层水平.在“是否含参”因素上完全采用武小鹏等人的划分,将“是否含参”划分为“无参数”和“有参数”两个水平.由于试卷中解答题分值占比较高,同时,一道数学解答题包含多个小问题,然后,不同的小问题之间有的相互联系,有的单独成立, 则会出现递进的梯度形式.因此, 对于解答题, 增加“梯度”因素.将“梯度”因素划分为两个水平分别为“问题单独成立”“问题间互相关联”.
依据上述模型对是否含参、运算水平、推理能力、知识含量、认知水平、梯度六大因素进行编码,以下图表为不同因素不同水平的内涵及权重[7]如表2 所示,这里将选用调整后的模型对2019 和2020年高考理科数学全国Ⅱ卷进行分析.

表2:综合难度系数模型各因素权重及内涵
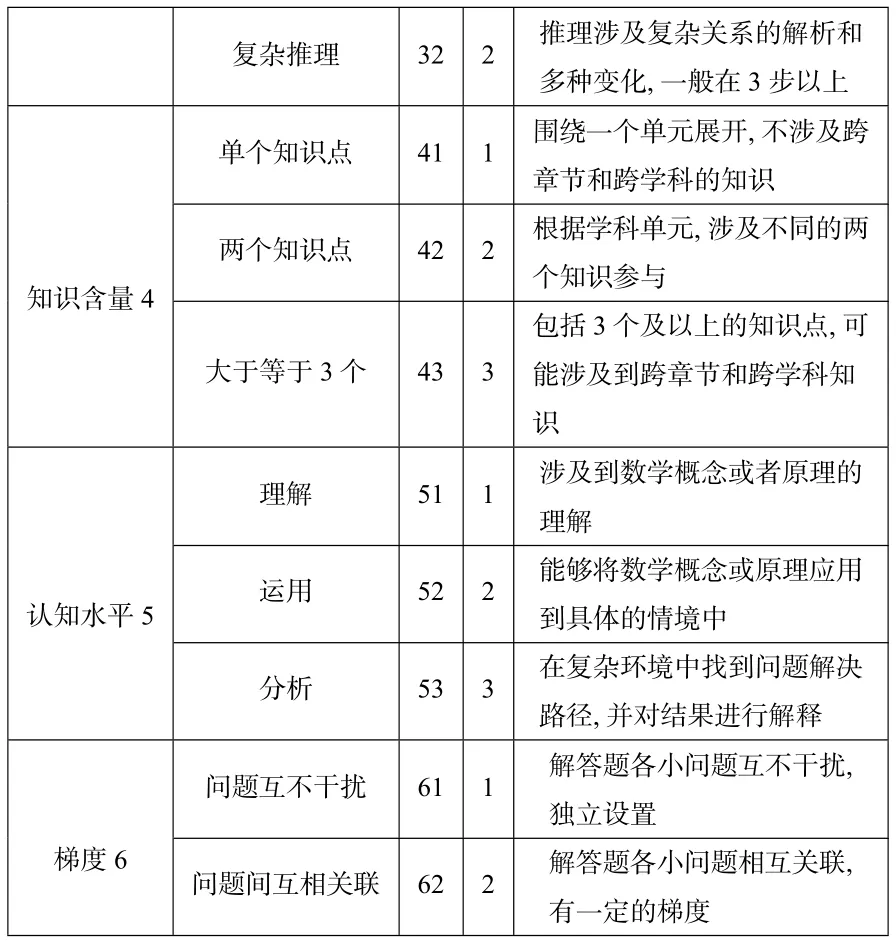
复杂推理32 2推理涉及复杂关系的解析和多种变化,一般在3 步以上知识含量4单个知识点41 1围绕一个单元展开,不涉及跨章节和跨学科的知识两个知识点42 2根据学科单元,涉及不同的两个知识参与大于等于3 个43 3包括3 个及以上的知识点,可能涉及到跨章节和跨学科知识认知水平5理解51 1涉及到数学概念或者原理的理解运用52 2能够将数学概念或原理应用到具体的情境中分析53 3在复杂环境中找到问题解决路径,并对结果进行解释梯度6问题互不干扰61 1解答题各小问题互不干扰,独立设置问题间互相关联62 2解答题各小问题相互关联,有一定的梯度
三、2019-2020年高考理科数学全国Ⅱ卷统计分析
本研究选取了2019 和2020年高考理科数学全国Ⅱ卷为研究对象,基于更改后的模型对试卷从“是否含参”、“运算水平”、“推理”、“知识含量”、“认知水平”、“梯度”这六个因素进行分析.
根据表1、表2 的定义对2019、2020年两套试题进行赋值编码.例如2020 高考理科试题全国Ⅱ卷第6 题、第10 题,2019年高考理科试题全国Ⅱ卷第8 题、第10 题,可编码如下:
例1(2020 高考全国Ⅱ卷理科第6 题) 数列{an}中,a1= 2,am+n=aman, 若ak+1+ak+2+···+ak+10=215−25,则k=
A.2 B.3 C.4 D.5
此题属于有参数、简单符号计算、简单推理、知识含量有两个知识点、运用类试题.
例2(2020年高考全国Ⅱ卷理科第10 题)已知∆ABC的面积为的等边三角形,且其顶点都在球O的球面上,若球O的表面积为16π,则O到平面ABC的距离为

此题属于无参数、复杂数值计算、复杂推理,知识含量三个及以上,分析水平的试题.
例3(2019年高考全国Ⅱ卷理科第8 题) 若抛物线y2= 2px(p >0)的焦点是椭圆= 1 的一个焦点,则p=
A.2 B.3 C.4 D.5
此题属于有参数、简单符号运算、简单推理、知识点为三个以上、运用水平的试题.
例4(2019年高考全国Ⅱ卷理科第20 题) 已知函数f(x)=lnx −
(1)讨论f(x)的单调性, 并证明f(x)有且仅有两个零点;
(2)设x0是f(x)的一个零点, 证明曲线y= lnx在点A(x0,lnx0)处的切线也是曲线y=ex的切线.
此题属于有参数、简单符号运算、复杂推理、知识含量三个以上、分析水平、问题单独成立互不干扰的试题.
上述例题可根据表2 中的各因素权重编码表如下所示:
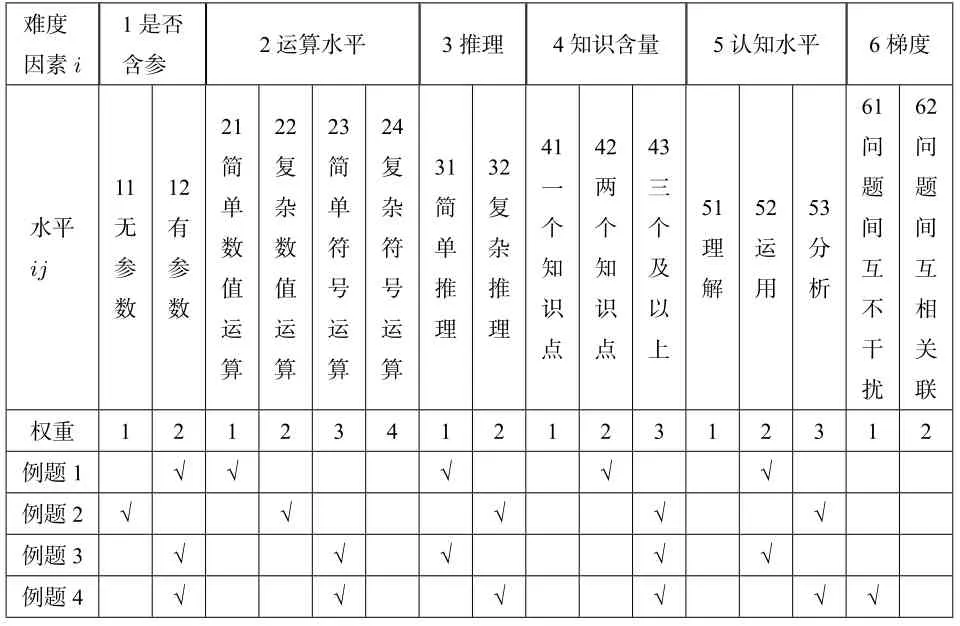
表3:例题难度系数编码表
按照表2 中的编码的各因素权重与内涵对2019年和2020年的两套高考试卷进行了编码,其中综合难度系数按照公式(1)计算得到.最终形成原编码数据表(略),通过计算统计得到表4.
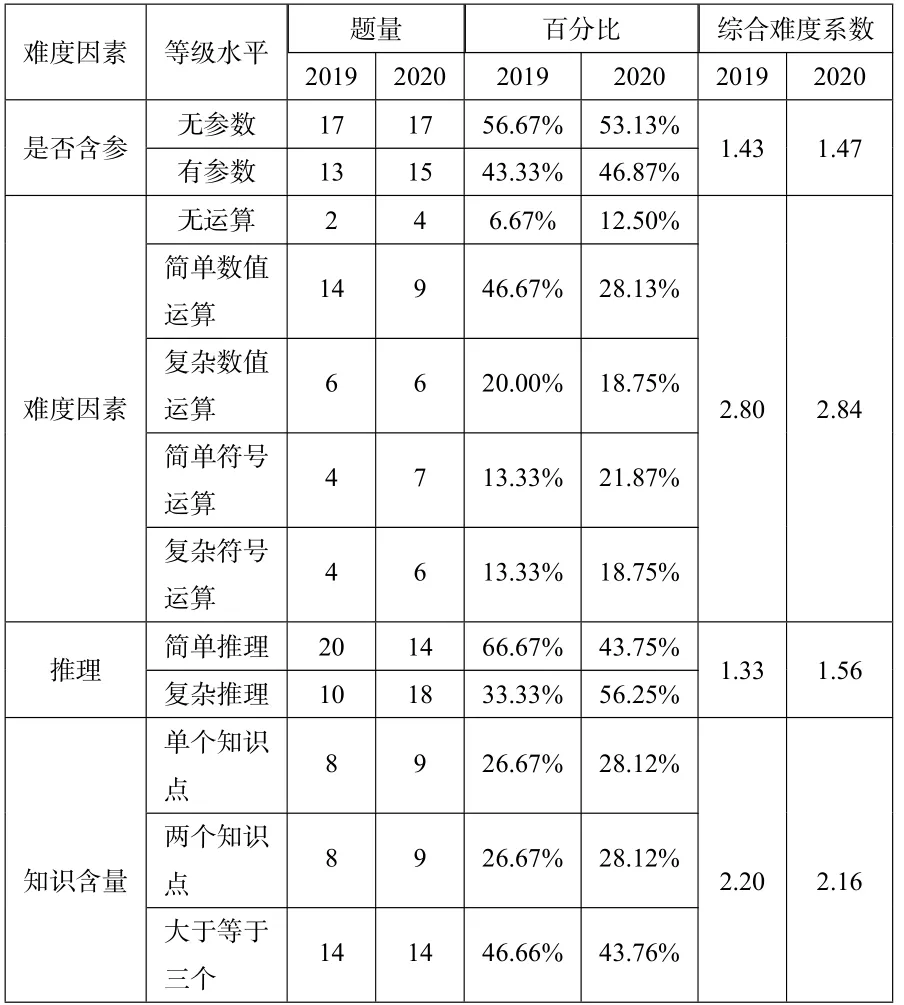
表4:2019 和2020年高考理科数学全国Ⅱ卷综合统计
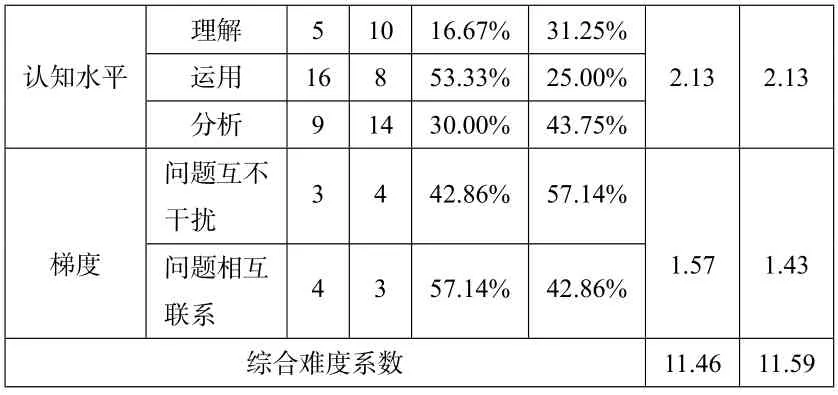
认知水平理解5 10 16.67%31.25%2.13 2.13运用16 8 53.33%25.00%分析9 14 30.00%43.75%梯度问题互不干扰3 4 42.86%57.14%1.57 1.43问题相互联系4 3 57.14%42.86%综合难度系数11.46 11.59
四、各难度因素的特征分析
根据表4 的统计结果,下面将以2019年和2020年高考理科数学全国Ⅱ卷的不同难度因素水平进行比较分析,以此为基础对高考考察的侧重点进行说明,最后利用综合难度模型雷达图做整体分析.
1.是否含参因素
根据统计表4, 按照是否含参因素中“无参数”、“有参数”两个水平各自所占的百分比绘制折线图如图1 所示.
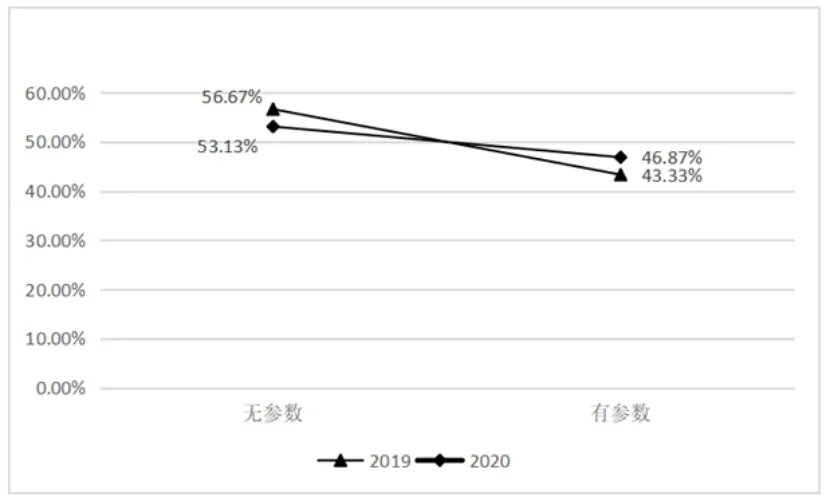
图1
在是否含参因素方面, 2019 和2020年无参数题目占比分别为56.67%、53.13%.有参数题目占比为43.44% 和46.87%.参数作为数学学科符号考察的方面,在高考题目中层出不穷.就这两年的试题而言,2020年有参数的题目数量多于2019年的题目数量.说明2020年高考理解相对抽象,题目难度加大.
2.运算水平因素
根据统计表4,按照无运算、简单数值运算、复杂数值运算、简单符号运算、复杂符号运算五种水平各自所占的百分比绘制折线图如图2 所示.
从上图可知,高考试题对于运算的考查较为全面,从无运算到复杂符号运算均有所涉及到的题目.就试题各自比例而言,2019年简单数值运算考查相对较多,2020年的考查较为均匀,比例相当.体现出高考试题对能力考查兼顾试题的基础性、综合性和应用性[3].也体现出不同学生有不同的能力发展的理念[8].就这两年的试题而言,在运算难度因素方面,2020年的试题对考生的运算水平要求相对较高,计算难度偏大.
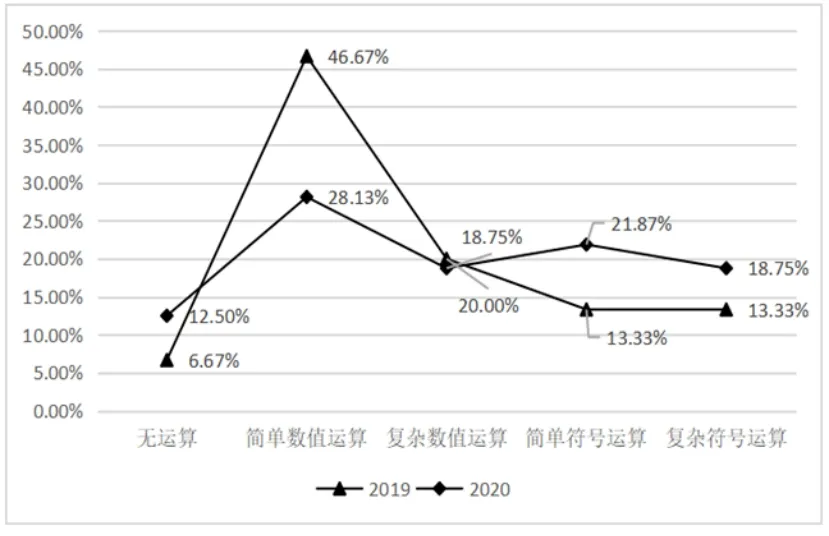
图2
3.推理能力因素
统计显示,2019年和2020年全国高考理科全国Ⅱ卷.按照简单推理、复杂推理两个水平按照所占百分比例绘制折线图如图3 所示.
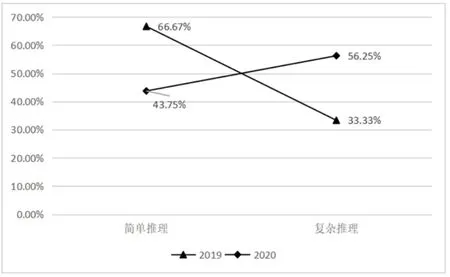
图3
在推理因素方面,2019 和2020年在简单推理题目占比分别为66.67%、43.75%.复杂推理题目占比分别为33.33%、56.25%.从试题分布来看对于推理论证能力和抽象能力的考查贯穿于全卷, 说明推理能力是高考试卷能力考察的重点,并强调高考试题具有科学性、严谨性、抽象性的特点,这与全国统一考试大纲相互呼应[3].就这两年试卷而言,2020年复杂推理方面的题目数量多于简单推理题目数量,复杂推理题目比例远高于2019年的比例.说明2020年的试题对学生的推理能力要求更严,标准更高.
4、知识含量因素根据统计表4,按照知识含量的三个水平,按照所占百分比例绘制出折线图,如图4 所示.
从统计表和图4 中,我们可以看到,高考试卷在知识含量方面,多以三个及以上的知识点为主,体现出高考试卷知识点考察的综合性.对于数学知识点的考察,既全面又突出重点.从试题分布方面来说,解答题主要是多个知识点的结合.对于高中教师说,在教学中应注重学生知识的迁移,关注不同章节不同学科多个知识点的联系和应用.在原有知识的基础上进一步加深拓展,逐级深化.就这两套试卷比较而言,知识含量基本相当,没有明显的差别.
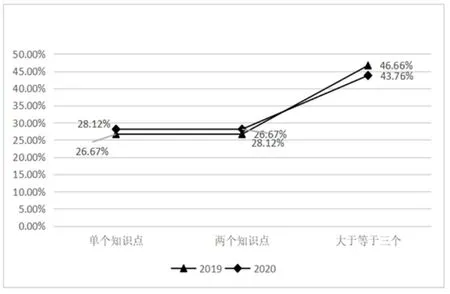
图4
5.认知水平因素
根据统计表4,对认知水平因素方面的理解、运用、分析三个水平各自所占百分比例绘制折线图如图5 所示.

图5
从上图可知,两套试卷在认知水平上都很注重理解、运用、分析这三个方面,不同认知水平的在试题中均有涉及,一定程度上体现了高考在认知因素考查上的全面性.从全卷试题分布来看,分析类题目多以解答题为主,选择题与填空题主要是理解与运用类,体现出高考试题的层次性.就试卷比较而言,2019年和2020年的试卷对于认知因素侧重不同,在分析水平的考察上,2020年明显高于2019年,对学生在复杂问题情境中寻找到解答途径的能力要求更高.因此,就认知水平方面,2020年的试卷难度明显高于2019年试卷.
6.梯度因素
梯度因素的统计结果见图6 所示.
由图6 可以看出,2019年和2020年全国高考理科全国Ⅱ卷在“梯度”因素方面存在着明显的差异,2019年的解答题中体现着“问题互不干扰”层次的题目比例低于2020年的试题,但,2019年属于“问题间相互联系”水平的题目所占比例高于2020年的试题,约高出14.28%.从梯度因素方面来看,2019年试题在解答题方面较2020年,小问题之间的关联更大,对学生的提出了更高的要求.
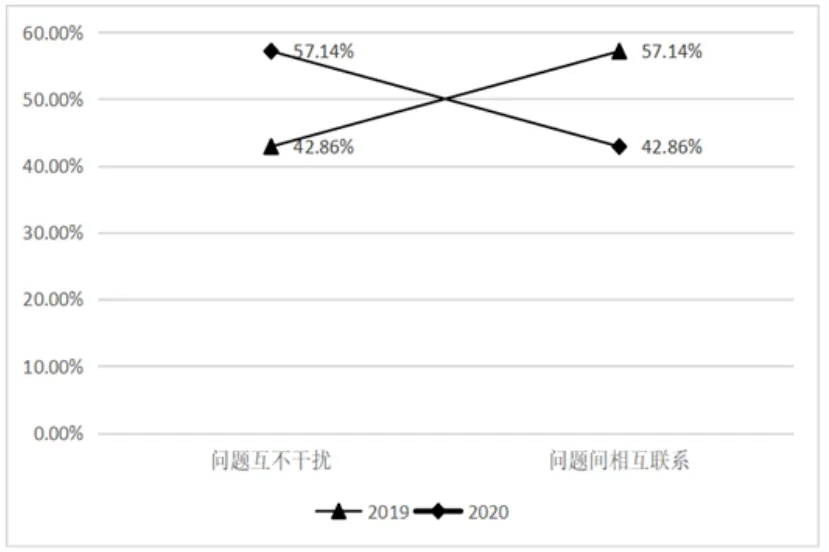
图6
7.综合难度系数分析
根据“是否含参”、“运算”“推理”、“知识含量”、“认知水平”、“梯度”这6 个因素在试题中的分布,为了进一步考察两卷的难度,对2019年和2020年全国高考理科数学全国Ⅱ卷不同因素不同水平的题目进行统计.利用综合难度系数计算公式(1)计算出各个因素的加权平均,得到以下结果如表5.
根据上表得到综合难度综合难度雷达图,如图7 所示.
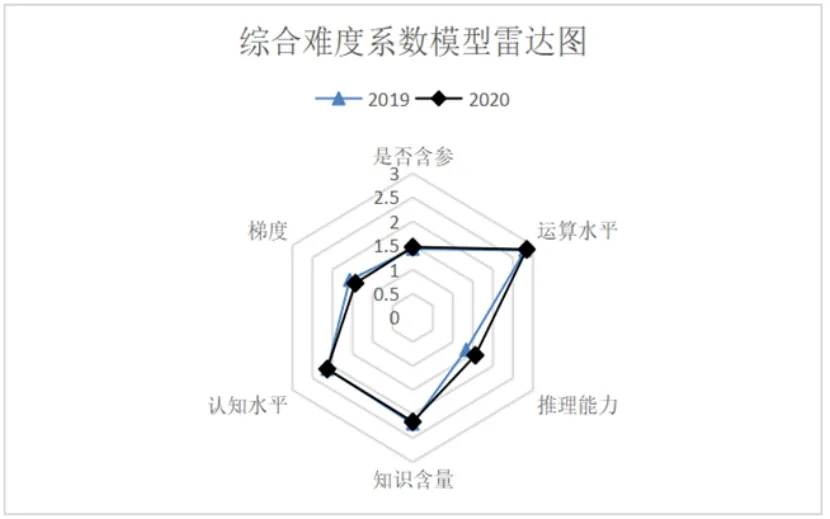
图7
根据图7 和表5,两套试题在是否含参、认知水平、运算水平、知识含量、推理能力、梯度这六个因素中,程度相当.在一定程度上, 说明了高考试题在考察数学基础知识的基础上,不仅注重数学方法的考察同时也注重考察数学能力,并呈现出在基本能力考察上的稳定性和一致性.在表5 中,可以看出2020年的总难度系数为11.59,2019年总难度系数为11.46.在雷达图的整体态势来看,2019年的考题在六个因素上,相对平衡; 在2020年的试卷上,强调考察学生的运算水平.因此,就两套试题而言,2020年试题在部分因素难度系数相对较大,难度相对较高.
需要说明的是,2019年和2020年的试题在试题数量和分值上有差异,分析可能会出现一些偏差.由于不同学生数学学习能力有差异性,针对同一试题,对于不同学生难度也不尽相同,因此综合难度系数只是一个理论值.
五、结论与启示
根据分析结果,我们发现,2020年高考理科数学全国Ⅱ卷的难度较2019年稳中求变,难度略有升高.两份试卷突出考察学生的运算能力,并且知识综合性较强.综合分析图表得到高考试题的以下特点.
(一)具有稳定性和全面性
在高考试卷中,对于是否含参、运算、推理、知识含量、认知水平、梯度方面的难度系数中趋于稳定,在卷面布局方面均以22 道必做题与1 道选做题组成,说明试卷布局稳定.在解答题方面以高中数学课程重点章节为主要考察对象,如三角函数、数列、函数、解析几何、立体几何,说明考察要点稳定.在客观题部分,考查基础知识的基础上,注重数学思想方法、数学能力的考查.从试卷总体来说,试题兼顾了基础性和综合性.从知识含量角度来看,内容分布均衡,问题多样化,既全面又突出重点,对于支撑学科知识体系的重要内容占有重要的比例,同时知识考察内容丰富而全面,具备全面性的特征.
(二)运算性与抽象性并举
运算求解能力是思维能力和运算技能的结合[1].统计数据表明,高考数学试题在“运算”因素的考察上,不仅有传统的简单数值运算,也有相当数量的符号运算.在客观题方面,数值运算居多,解答题方面多以符号运算与复杂数值运算为主.这充分说明高考试卷突出考察学生运算能力.就两套试卷而言,2019年和2020年的试卷在运算因素上,2020年试题计算量增多,对学生运算能力要求更高,试卷难度更大.
在推理因素方面,不仅有清晰的简单逻辑推理也有复杂的逻辑推理.符合课程标准中的让不同学生有不同的发展的要求.2020年试卷在推理因素上的难度系数明显高于2019年,这说明试卷对学生的逻辑推理能力有更高的标准.因此,高考试卷一定会考察学生的基础运算能力,还会要求学生根据问题条件从大量的数据中抽选出有用信息,进行合理的推断、分析,选择快捷的运算途径,最终得出结果.高中教师在日常教学工作中,要注重对学生推理、归纳、总结的能力的培养,让学生习惯于对数学公式进行推导,体会数学的公理化体系.
(三)兼顾综合性和系统性
数学学科的系统性和严密性决定了数学知识之间深刻的内在联系,包括各部分知识的纵向联系和横向联系[3].解答题方面尤其注重在知识网络的交汇点处设计试题,对知识点进行综合考察,使得对数学基础知识的考察达到必要的深度.试题不但系统性地考察学生的数学思想、逻辑推理、运算能力,而且让学生洞察到数学学科的美丽与全貌,因而,高考试题中的综合性和系统性特点不容小觑.
基于以上研究,建议命题者在优化试题结构,科学合理命题的同时,充分利用综合难度系数模型对试卷做难度预测,并对每个题目进行深层次的分析与评价,准确把握试卷难度,从而使考题设置科学合理,努力实现考察数学综合素养的要求.
