剖析向量高考题 抓准复习着力点
2021-03-17上海南汇中学201399
上海南汇中学(201399) 宋 磊
1 高考对向量的考查内容和要求
《普通高中数学课程标准(2017年版2020年修订)》对向量进行了刻画: 向量理论具有深刻的数学内涵、丰富的物理背景.向量既是代数研究对象,也是几何研究对象,是沟通几何与代数的桥梁,是描述直线、曲线、平面、曲面以及高维空间数学问题的基本工具,是进一步学习和研究其他数学领域问题的基础,在解决实际问题中发挥重要作用.基于向量的重要性,平面向量是高考的重要考点之一.
高考对平面向量的考查主要有三个层面: 知识层面,直接考查向量的线性运算、数量积、垂直或平行关系、基底、模与夹角、向量基本定理等;方法层面,重点考查数形结合、转化与化归、分类讨论、函数与方程等思想方法;素养层面,主要考查数学运算、直观想象、逻辑推理和数学建模等核心素养.2020年全国高考向量试题遵循了“考查基础知识的同时,注重了思想方法和核心素养考查”的原则,很好地考查了知识点、思想方法和数学素养.
2 2020年高考向量试题剖析
平面向量融数、形于一体, 具有几何和代数的“双重身份”,由于其知识的特点,在试题的基础性、综合性、灵活性、创新性、难度设计和区分度设计等方面提供了广泛的试题命制空间,因而决定了其必然会成为历年高考试题中的热点内容.笔者以2020年高考数学全国文理和各省市真题卷为例,撷取若干典型问题剖析,以期找寻试题中所含知识要点、思想方法,探求数学本质,感悟核心素养,进而指导和反思向量教学,为2021年高考复习抓准着力点.
2.1 注重向量基本运算
低中难度的向量问题考查基本上是基于线性运算和数量积运算, 以符号形式和坐标形式两种方式, 展开平行、垂直、夹角、模等问题的考查.
例1(2020年高考新课标Ⅰ卷文科第14 题) 设向量a=(1,−1),b=(m+1,2m −4),若a⊥b,则m=____.
例2(2020年高考新课标Ⅲ卷文科第6 题)在平面内,A,B是两个定点,C是动点,若−A→C ·−B−→C= 1,则点C的轨迹为( )
A.圆 B.椭圆 C.抛物线 D.直线
例3(2020年高考新课标Ⅱ卷理科第13 题)已知单位向量a,b的夹角为45◦,ka −b与a垂直,则k=____.
例4(2020年高考新课标Ⅲ卷理科第6 题) 已知 向 量a,b满 足|a|= 5,|b|= 6,a · b=−6,则cos〈a,a+b〉=( ).
例5(2020年高考新课标Ⅰ卷理科第14 题)设a,b为单位向量,且|a+b|=1,则|a −b|=____.
例6(2020年高考北京卷第13 题)已知正方形ABCD的边长为2,点P满足则=____;=____.
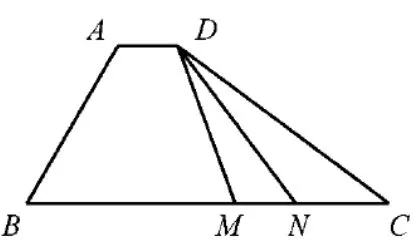
例7(2020年高考天津卷第15 题) 如图, 在四边形ABCD中,∠B= 60◦,AB=3,BC= 6, 且则实数λ的值为____,若M,N是线段BC上的动点,且的最小值为____.
2.2 注重代数运算与几何推理相结合
由于向量是沟通代数与几何的有力工具,向量问题的解决途径一般有两个: 一是代数法, 从向量的线性运算、数量积、平面向量基本定理以及坐标表示等方面思考,将问题转化为代数中的有关问题解决;二是几何法,通过向量的几何意义以及向量的基本运算将其转化为平面几何问题.很多向量的综合问题需要代数运算与几何推理相结合.
例8(2020年高考上海卷第12 题)已知平面向量a1,a2,b1,b2,··· ,bk(k ∈N∗) 是平面内两两互不相等的向量,|a1−a2|= 1, 且对任意的i= 1,2 及j= 1,2,··· ,k,|ai −bj|∈{1,2},则k最大值为____.
解析不妨设a1== (0,0),a2=(1,0), 则bj=(x,y),由|ai −bj| ∈{1,2},可得:= 1或√= 2, 且故点Bj位于以原点为圆心,1 或2 为半径的圆上,并且位于以(1,0)为圆心,1 或2 为半径的圆上,故k的最大值即为图中所示的交点个数.

2.3 突出向量与其它知识的交汇
向量是沟通代数与几何的重要工具,是联系不等式、函数、三角、数列、几何等多项内容的桥梁.因此,向量与其它知识的交汇自然深受高考命题专家的青睐.
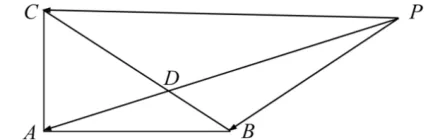
例9(2020年高考江苏卷第13 题)在∆ABC中,AB=4,AC=3,∠BAC=90◦,D在边BC上, 延长AD到P, 使得AP= 9, 若为常数), 则CD的长度是____.
方法1由A,D,P三点共线, 可设若m ̸=0 且m ̸=,则B,D,C三点共线, 故λm+−m) = 1, 解得λ=, 由AP= 9得AD= 3.由AB= 4,AC= 3, ∠BAC= 90◦, 得BC= 5, 故cos ∠ACD=在∆ACD中, 由余弦定理,cos ∠ACD=解得CD=若m= 0,则C,D重合,此时CD的长度为0.若m=则重合,此时PA=12,不合题意,舍去.
综上,CD的长度为0 或
方法2设化简整理, 得=−2ma+ (2m −3)b, 两边平方, 得=4m2a2+(2m −3)2b2,即81=64m2+9(2m −3)2,解得m=0 或m=若m=0,则重合,此时CD的长度为0.若m=设
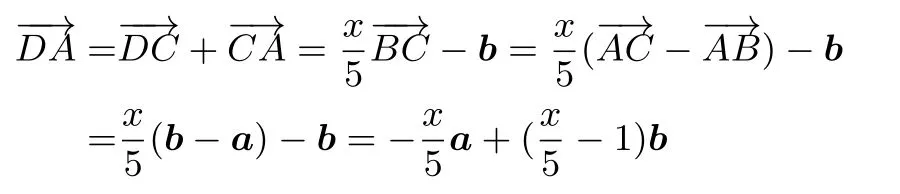
综上,CD的长度为0 或
方法3以A为原点,AB所在直线为x轴,AC所在直线为y轴, 建立平面直角坐标系, 则A(0,0),B(4,0),C(0,3),设P(x,y),由得(−x,−y)=m(4−x,−y)+−m)(−x,3−y),故化简整理, 得故P(8m,9−6m),由AP=9,得(8m)2+(9−6m)2= 81, 解得m= 0 或m=若m= 0, 则重合,此时CD的长度为0.若m=则直线PA的方程lP A:y=直线BC的方程为lBC:y=联立方程解得故
综上,CD的长度为0 或
方法4以A为原点,AB所在直线为x轴,AC所在直线为y轴, 建立平面直角坐标系, 设∠PAB=θ, 则A(0,0),B(4,0),C(0,3),P(9 cosθ,9 sinθ),由得(−9 cosθ,−9 sinθ) =m(4−9 cosθ,−9 sinθ)+−m)(−9 cosθ,3−9 sinθ),故化简整理,得解得m=0 或m=下同方法3.
评析方法1 利用了平面向量共线定理及余弦定理,通过解三角形的方法求出答案;方法2 利用平面向量基本定理,采用基底法;方法3 利用坐标法,结合解析几何相关知识解决;方法4 结合三角,采用参数法,利用坐标解决.
例10(2020年高考浙江卷第17 题)设e1,e2为单位向量,满足a=e1+e2,b=3e1+e2,设a,b的夹角为θ,则cos2θ的最小值为____.
方法1由|2e1−e2|≤√得4−4e1·e2+1 ≤2,即e1·e2≥由e1,e2为单位向量,从而e1·e2∈令t=e1·e2,则
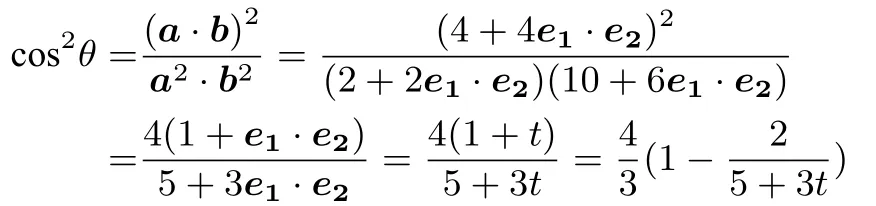
而y=上 单调递 增, 故cos2θ ∈从而cos2θ的最小值为
方法2设单位向量e1、e2所成的夹角为α, 则由|2e1−e2|≤即4−4 cosα+1 ≤2, 故cosα≥故cosα ∈a · b= (e1+e2)·(3e1+e2) = 4+4 cosα,|a|2=|e1+e2|2= 2+2 cosα,|b|2=|3e1+e2|2=10+6 cosα,从而cos2θ==,令t=3 cosα+5,则,故cos2θ=时,(cos2θ)min=
方法3设e1= (1,0),e2= (cosα,sinα), 则a=e1+e2=(1+cosα,sinα),b=3e1+e2=(3+cosα,sinα).由故由

得cos2θ=下同方法2.
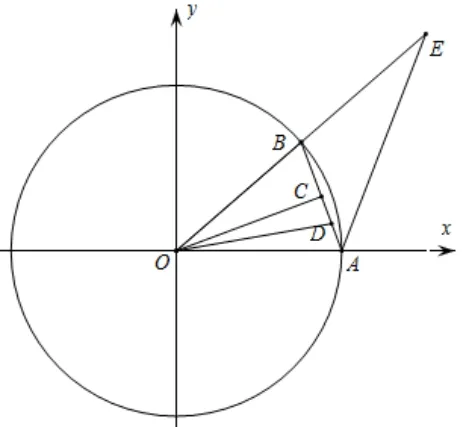
方法4如图, 在单位圆中, 取e1=e2=2e2=连结AB, 取AB的中点 为C,AC的中点为D.由|2e1−e2|≤得|AE|≤故cos ∠AOB≥可得|AB|≤即故a与b的夹角θ即的夹角∠COD, 故cos2θ= cos2∠COD==令|AB|=t, 则cos2θ=可得故(cos2θ)min=
评析方法1、2 均采用代数法符号运算,结合不等式、函数相关知识解决;方法3 采用坐标法;方法4 是转化为几何法解决.
3 抓准向量“三核心”,强化向量“四意识”
通过对2020 高考向量试题的剖析,可以帮助我们抓准复习的着力点,建构2021 高考复习的框架.笔者认为,应当抓准向量“三核心”,强化向量“四意识”.
3.1 向量“三核心”
向量复习的第一个核心是加强基本概念与基本运算的复习,主要包括平面向量基本定理、向量的模的运算和几何意义、向量的线性运算、共线向量、向量数量积及相关的向量夹角与向量垂直等内容,基本运算包括符号形式与坐标形式.
向量复习的第二个核心是明确向量代数与几何双角色,凸显双性.在复习过程中,例题的示范要凸显双性,如上文例9、例10 一样,让学生感受到手中有两招,可选择可优化,形成代数与几何这两个解题流程.
向量复习的第三个核心是注重平面向量运算工具的灵活使用,纵横交汇.由于平面向量作为沟通代数与几何的桥梁,其研究几何图形性质的工具性的作用非常明显,因此,以平面向量为背景或利用平面向量作为解题工具来命制高考试题,是数学高考试题命制的常见方法.在全面复习的基础上,重视对主干知识和重要思想方法的掌握,掌握向量在知识交汇处的主要考查途径和解决方式,让学生体会关于高考数学命题的新理念.
3.2 向量“四意识”
第一,向量复习要有“坐标意识”.“坐标法”是解决向量问题的重要途径,其优点是思维方式比较“固定”,学生容易掌握.坐标法的关键是合理建立直角坐标系,准确算出关键点的坐标.如上文例2、例6、例7 均可以用坐标法解决.
第二,向量复习要有“几何意识”.我们要引导学生主动挖掘向量问题的几何背景用以解题.很多时候,我们如果能将向量问题置于适当的几何背景之中,就能够使抽象问题直观化,将复杂的代数问题转化为几何问题,从而快速求解.
第三,向量复习要有“投影意识”.向量的数量积是向量非常重要的核心知识,而投影是对向量数量积本质的理解和把握, 在向量复习中要强化向量投影的意义和价值的认识.在解决向量数量积问题时,利用投影可能会事半功倍.
例11(2020年高考山东卷第7 题)已知P是边长为2的正六边形ABCDEF内的一点,则的取值范围是( )
A.(−2,6) B.(−6,2) C.(−2,4) D.(−4,6)
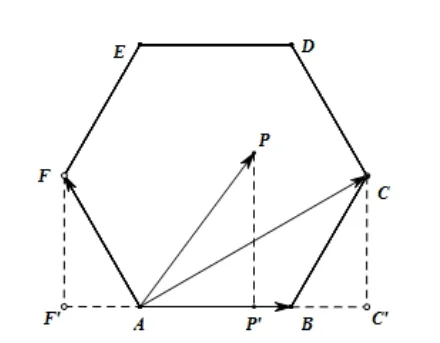
解析如图,根据正六边形的特征, 可以得到方向上的投影的取值范围是(−1,3),结合向量数量积的几何意义,可知的模与方向上的投影的乘积,所以的取值范围是(−2,6).
第四,向量复习要有“基底意识”.平面向量基本定理是向量知识体系中占有核心地位的定理,而“基底意识”的本质就是平面向量基本定理的灵活运用,难点是如何选择“基底”用于简化运算.上文中,例6、例7、例9、例10 都可以用“基底思想”来解决.
