一类具有比例时滞神经网络的全局幂稳定

谭服好，关开中

（五邑大学 数学与计算科学学院，广东 江门 529020）

自Chua 和Yang[1]提出细胞神经网络以来，其在聚类、图像处理、模式识别、优化问题等领域中的应用引起了广泛的研究[2-4]. 时滞不可避免地存在于神经网络中，并导致系统性能变差甚至不稳定，因此研究时滞对神经网络稳定性的影响具有重要的理论和实际意义. 比例时滞作为一类特殊的时滞类型存在于非线性系统和电动力学等领域[5-7]. 特别地，由于神经网络的“空间”属性以及比例时滞具有可控性和可预测性的优点，近年来，人们将比例时滞引入到神经网络中，并研究了各类比例时滞神经网络的稳定性问题. 文献[8]运用M-矩阵理论构造合适的Lyapunov 泛函，研究了一类比例时滞细胞神经网络的稳定性问题，建立了该神经网络平衡点的全局渐近稳定性条件，该条件是与时滞相关的. 文献[9]利用M-矩阵理论和不等式技巧，进一步研究了一类非自治比例时滞神经网络的稳定性，并获得了此类系统平衡点全局幂稳定的条件，但该条件是时滞无关的. 注意到，渐近稳定弱于幂稳定，且时滞有关的条件比时滞无关的相对更不保守，因此建立时滞有关的幂稳定性条件更有意义. 基于此，本文将建立一个新的Razumikhin 条件，并利用Lyapunov-Razumikhin 方法，尝试构建一类比例时滞神经网络平衡点与时滞有关的全局幂稳定条件，以期所得结果能够改进已有文献的结论.

1 模型与预备知识

设R 为实数集， R+为非负实数集， Rm表示具有范数的m维实线性赋范空间. 记C(R+, R+)={ψ: R+→R+是连续的}， K={u∈C(R+, R+):u(0) =0且u(s)关于s是严格递增的}，sgn(y)表示y的符号函数.

考虑以下具有比例时滞的神经网络模型：

这里yi(t)表示第i个神经元在t时刻的状态变量，q∈ (0,1)为比例因子，(1 -q)t为网络传输时滞函数，表示t时刻第i个神经元的自反馈强度；分别表示第j个神经元到第i个神经元在t时刻和qt时刻的连接强度；为yi(t)在t=0时刻的初始值，gi表示激活函数且满足下面的条件：

其中，li是非负常数，i=1,2, … ,m.记

定义1称为系统（1）的平衡点，如果其满足

由式（2），容易看出系统（1）具有平衡点(0, …, 0)T∈Rm.

为了研究系统（1）平衡点的稳定性，我们先研究下列一般的比例时滞微分系统：

本文总假定函数f满足一定的条件使得系统（3）在(0, +∞)存在唯一解. 注意到f(t, 0,0) =0，因此y(t) =0是系统（3）具有初始条件y(0) =0的平凡解.

定义2[5-6]令y(t)是系统（1）中的解，函数V: R+× Rm→R+为连续，则V沿该解的右上导数定义为：

定义3令y(t)是系统（3）的解，如果存在常数λ＞ 0和函数μ,ν∈K ，使得

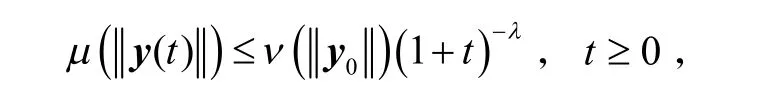
则称系统（3）的平凡解是全局弱幂稳定的. 特别地，当μ(s) =ν(s)=s时，称系统（3）的平凡解是全局幂稳定的.

2 主要结果

在本节中，我们将利用Lyapunov-Razumikhin 方法，建立系统（3）的平凡解和系统（1）的平衡点为全局幂稳定的条件.

定理1如果存在常数η＞ 0，ω,h∈C(R+, R+)，函数μ,ν∈K ，以及连续函数V(t,y) : R+×Rm→R，使得：

则系统（1）的平凡解是全局弱幂稳定的.

证明由条件可选取常数λ＞ 0满足

设V(t)=V(t,y(t))和Φ(t)=(1 +t)λV(t)，其中y(t)是系统（3）的解，易得Φ(t)≥V(t)，t≥ 0. 由i）得：下面证明：

注意到Φ(0)=V(0)，若式（5）不是对所有的t≥ 0成立，则存在使得进一步，存在＞0，得：

0＜q＜1，得即

计算可得：

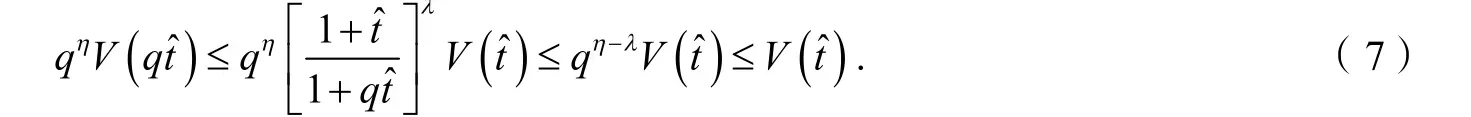
这就与式（6）中的最后一个不等式矛盾，定理得证.

推论1如果将定理1 中的条件i）替换为条件其中a,b和p是正数，则系统（3）的平凡解是全局幂稳定的.

下面利用定理1，建立神经网络（1）平衡点的全局幂稳定条件.

定理2如果式（2）成立且存在常数η＞ 0，使得

证明设y(t)是系统（1）的解，令根据式（2），并计算V(t)沿系统（1）解的右上导数，可得：

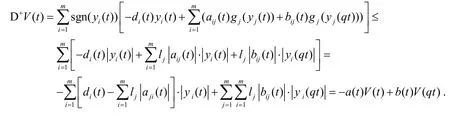
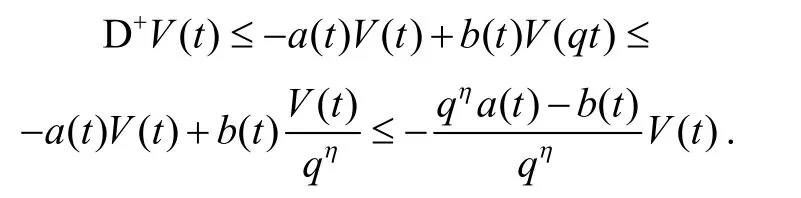
注1令其中由文献[9]中的定理3.2 可得: 如果矩阵-M是非奇异的M-矩阵，则系统（1）的零解是全局幂稳定的.

3 数值算例

在本节中，我们将给出两个数值例子来说明所得结果的有效性和合理性.

例1考虑以下具有比例时滞的神经网络：

取η=1，计算可得ρ=0.5＞0，从而定理2 的条件满足，因此系统（9）的平衡点是全局幂稳定的且收敛阶为1. 给定初值y(0) =0.5，运用Matlab 工具箱得到系统（9）的状态轨迹如图1 所示.

例2考虑下面具有比例时滞的二维神经网络：

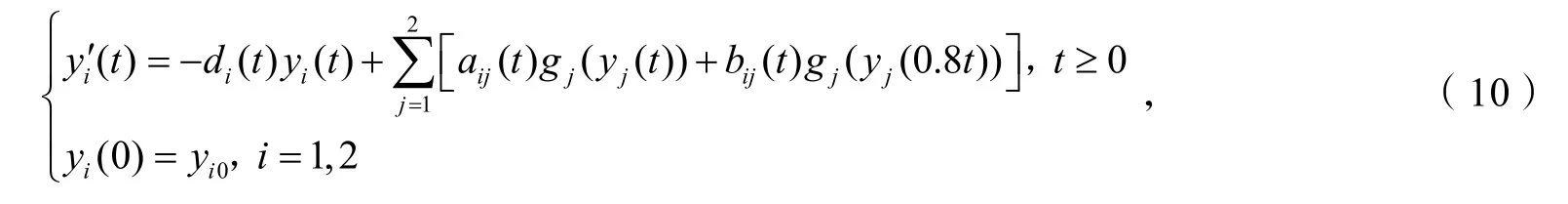
容易验证gi满足式（2）的条件且取η=1，经计算得a(t)=1 .5,b(t)=1 ,ρ=0.2＞0，故满足定理2 的条件，因此系统（10）的平衡点是幂稳定的. 图2 描述了系统（10）具有初始值y(0) =(0.8,0.4)T的状态.

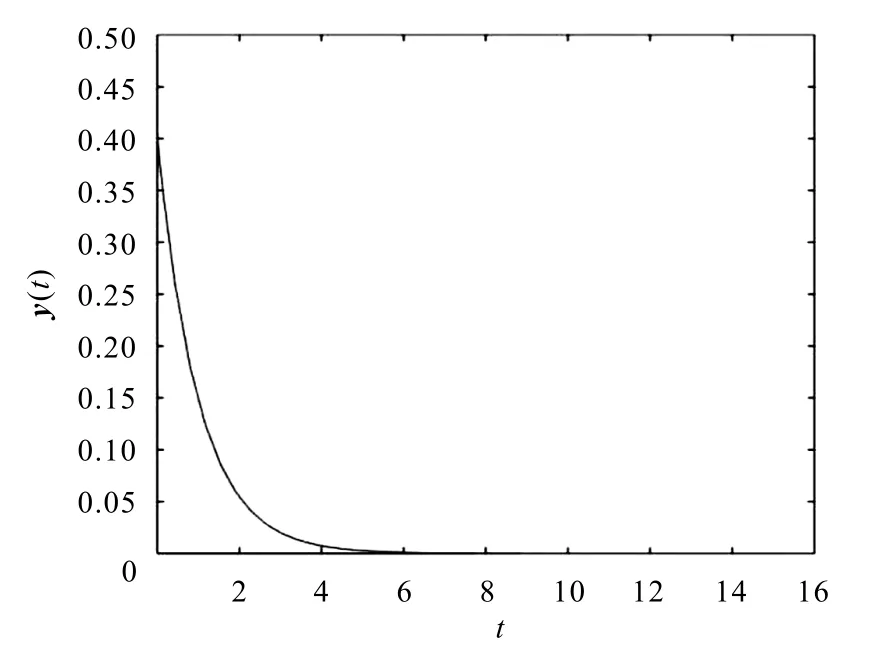
图1 系统(9)具有初始值y(0) =0.5的状态轨迹

图2 系统(10)具有初始值y(0) =(0.8,0.4)T的状态轨迹

注2简单计算，可得容易验证，矩阵-M不是非奇异的M-矩阵. 因此，根据注1，文献[9]中的定理3.2 不能应用于例2. 因此，我们的结果在一定程度上改进了文献[9]的相应结果.