不同表面凸起单元制动盘的热应力仿真分析
2021-03-17常宁黄尊地
常宁,黄尊地
(五邑大学 轨道交通学院,广东 江门 529020)
高速运行的轨道车辆速度突然降低时,其动能大部分会转变成制动盘与闸片接触生成的热能.由于制动盘与闸片的接触面积和散热效率有限,使得热量大量堆积,盘体温度急剧升高,导致盘体表面出现热裂痕而影响到车辆制动盘的寿命,甚至威胁列车的运行安全[1-3]. 随着列车行驶速度越来越快,制动盘表面单位面积分到的热量也越来越多,因此,研究列车处于减速状态时制动盘的散热情况,探究制动盘表面形态对其热量扩散的影响规律对优化制动盘性能有很大的意义.
目前,制动盘散热性能分析主要从改变制动盘材料[4]、优化制动盘散热筋结构[5]、优化仿真边界条件[6]、改变制动的盘表面结构[7]等方面开展研究. 现有研究中,多是通过在制动盘表面增加沟槽以改变制动盘的表面结构来研究表面微结构改变对制动盘散热性能的影响,很少考虑表面凸起结构对制动盘散热性能的影响. 本文基于热固耦合原理,以某型动车组制动盘为研究对象,建立常规光滑型、球型和堤坝型三种不同形状表面凸起单元的制动盘模型,对其进行热应力仿真分析,探究表面凸起单元对制动盘散热性能的影响,以期为制动盘热性能优化提供新的思路.
1 制动盘的结构与相关参数
1.1 制动盘结构参数
本文以某型动车组制动轴盘为研究对象建立常规制动盘模型,其结构参数如表1 所示.

表1 常规光滑型制动盘结构参数
为了改变制动性能,在常规制动盘表面增加球型和堤坝型两种表面凸起单元,建立带凸起的制动盘. 为确保制动过程平顺,在建立表面具有凸起单元的制动盘时,需要考虑凸起单元的密度. 堤坝型凸起制动盘在盘表面沿周向分布24 个凸起单元;球型凸起制动盘在盘表面沿周向分布24 个凸起单元,沿径向分布三层凸起单元. 制动盘模型如图1 所示.

图1 制动盘几何模型
仿真分析时认为制动盘材料为各向同性材料,材料性能不随温度变化而变化,3 种类型的制动盘盘体采用的材料具体参数如表2 所示.

表2 制动盘材料参数
1.2 制动工况
当列车碰到突发事件的时候,司机会实施紧急制动. 紧急制动持续的时间短,对制动盘的考验大,本文选取如表3 所示的紧急制动工况进行制动盘热性能分析.

表3 紧急制动工况参数
2 热分析模型边界条件及工况
在制动过程中,制动盘和闸片摩擦将动能转化为摩擦副间的热能,其间的热量传递方式有热传导、热对流、热辐射[8]. 由于制动作用时间较短,本文在分析时忽略热辐射对制动过程中温度场的影响,只考虑热传导和热对流[9].
2.1 热流密度
本文分析时将摩擦片与盘体摩擦产生的热能平均分配到整个盘体的摩擦面上,采用能量折算法求出的热量值均匀排布在摩擦表面上. 取热量转化率η= 0.9,每根轴上的摩擦面数为n,假设从制动开始到制动后t秒的过程中列车动能全部转化为热能,则由能量守恒定律可得出每个摩擦面吸收的热能[10]:

其中,M为轴重,kg;vt为制动t秒后的列车速度,m/s.
假定热量在全部接触面上平均分配,热流密度可以表达为:
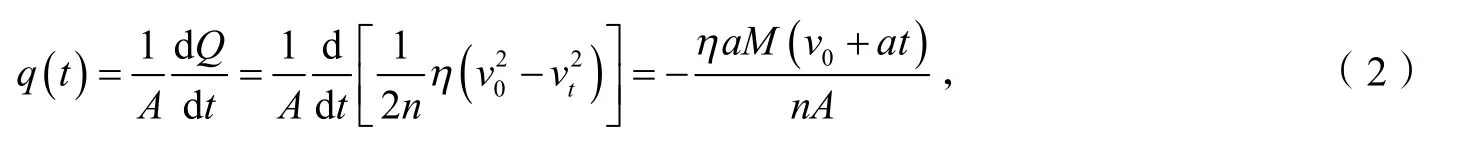
其中,A为单个摩擦面的面积, m2;a为制动减速度, m/s2.
将各个参数代入公式化简后,得热流密度计算公式为:

其中,常规制动盘的摩擦面积为 9.01 ×105mm2,堤坝型凸起制动盘的摩擦面积 1.31 ×105mm2,球型凸起制动盘的摩擦面积 1.01 ×105mm2.
2.2 对流换热模型
高速轨道车辆施行紧急制动时,制动盘位于高速流动的空气当中,此时的对流换热方式是受迫对流. 制动结束后列车停止运动,制动盘处于静止的空气场,此时的对流换热方式是自然对流. 对流换热系数h由多个因素共同影响,包括物体的外观、周围流体的流动条件等[11]. 本文采用的换热系数是平均换热系数,其计算公式为:

其中,t为时间,s;r为制动盘的径向半径,m;Pr为普兰特常数,取0.703;v为空气运动粘度,取 14.8 ×10-6m2/s ;λ为空气导热率,取 2.59 ×10-2W/((m⋅℃).
将各个参数代入公式简化后,得平均对流换热系数计算公式为:

2.3 载荷约束条件
在ANSYS 热分析环境中,热边界的约束方式通过以下过程来实现:
1)计算所得到的热流密度是以时间为单一变量的函数,在ANSYS 软件中可以通过一维函数来实现.
2)制动盘与其所处环境的空气产生的换热系数添加在制动盘的各个表面上,其中,对流换热系数有两个变量,即时间和制动盘的径向尺寸,以二维函数的形式在ANSYS 中实现.
3)初始温度载荷设定为22℃.
4)制动盘固定于车轴上且随着轮对旋转,对制动盘内圈x轴、y轴和z轴三个轴向上的平移施加约束条件.
3 结果与分析
3.1 温度场仿真结果与分析
1)列车在紧急制动时,制动盘和闸片发生摩擦产生了巨大的热量. 本文通过施加热流密度来模拟列车制动时制动盘产生的热量,热对流通过对流换热系数进行仿真.输入边界条件和相关参数进行仿真计算,得到如图2 所示的仿真结果. 从图2可以看出:在制动初期,制动盘的温度不断升高,此时处于高速空气流场中,制动盘的对流换热方式是受迫对流,盘体拥有比较高的对流换热系数,但制动盘表面的热量输入量依然远大于制动盘通过热传导和热对流传导到盘体其他区域或者消散到大气中的总量. 随着制动的进行,制动盘与空气的对流换热加强,温度有所下降. 制动结束53 s,在3 种制动盘当中,光滑制动盘的温度最高,有球型凸起的制动盘温度最低.

图2 三种制动盘的温度变化曲线图
图3为三种制动盘最高温度时的温度场云图. 通过仿真分析可知,在不同时刻,三种制动盘的最高温度集中在摩擦环上,光滑制动盘的最高温度较低,具有球型凸起的制动盘其最高温度最高. 此时的温度主要取决于摩擦面积,光滑制动盘的摩擦面积最大,单位面积分到的热量小,最高温度较低. 和光滑盘相比较,有凸起的制动盘除摩擦面外,其他区域温度则要低得多.

图3 三种制动盘最高温度时的温度分布云图
2)三种制动盘仿真的温度数据如表4 所示. 由表4 可知:表面带凸起的制动盘比常规光滑制动盘的温升速率高、最高温度高,但结束时温度低,其温度降比分别为16.8%、27.3%、71.7%.

表4 制动盘温度仿真结果对比
3.2 热应力场仿真结果分析
1)将上述温度场仿真计算所得的结果以边界条件的形式导入应力场进行热应力仿真分析,得到如图4 所示的制动盘不同时刻的热应力结果. 从图4可以看出:三种盘体最大应力的趋势都是先升高后降低,再缓慢上升. 第一次升高是由于制动盘摩擦面温度快速升高,导致了摩擦面和其他区域产生极大的温度差,从而引起应力上升,最高应力值在摩擦面上. 随着热量的传递,内圈处积累的热量也越来越多,材料膨胀受到限制,最终导致了盘体的内圈应力集中,出现了第二次应力上升.
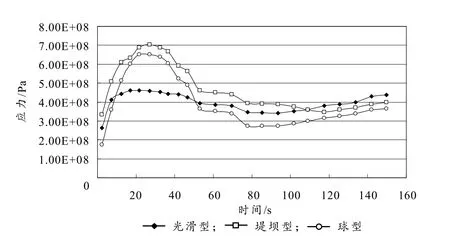
图4 三种制动盘的应力变化曲线图
表面凸起制动盘应力的第一个极值都比光滑制动盘大,原因是表面凸起制动盘的摩擦面积相对小,导致温度梯度更大,产生的热应力也更大. 在制动结束后,由于表面凸起制动盘暴露在大气中的面积更大,存在热量消散的连通通道,在散热上更具有优越性,在达到最大应力后,表面凸起制动盘的应力快速下降. 在应力第二次上升的时候,表面凸起制动盘的应力值均低于常规制动盘的应力值. 球型制动盘的应力值上升最快,也下降最快.
对于具有不同凸起的制动盘,应力变化不仅与制动盘温度有关,还与制动盘外形结构有关,因此三种制动盘应力达到最大值的时间、位置有差别. 图5 为三种制动盘最大应力时的热应力场分布云图. 从图5 可以看出:最大应力主要分布在制动盘与闸片的摩擦面上、凸起单元之间的平面上以及制动盘的内圈壁面上. 与常规制动盘相比,具有凸起单元的制动盘除上述区域应力较高外,其余位置应力都较低.

图5 三种制动盘最大应力时的热应力分布云图
2)三种制动盘应力仿真结果如表5 所示. 由表5 可知:表面带凸起的制动盘比常规制动盘应力上升速率更大、最大应力更高,结束时应力更低,其应力降比分别为23.7%、46.1%、55.4%.

表5 制动盘应力仿真结果对比
4 结论
本文在常规光滑型制动盘的基础上,增加了表面凸起单元,建立了堤坝型和球型两种表面凸起的制动盘,借助软件对3 种制动盘进行热应力仿真分析,结论如下:
1)表面带凸起的制动盘温度、应力变化率较大,常规制动盘温度、应力变化较缓. 制动结束后表面带凸起的制动盘温度、应力都低于常规制动盘. 结束时温度降比分别为16.8%、27.3%、71.7%,应力降比分别为23.7%、46.1%、55.4%. 表面带凸起的制动盘降温较快,对提高盘体散热性能、降低制动盘表面温度和应力有较好效果,其中,表面球型凸起的制动盘散热效果最佳.
2)在制动盘表面增加凸起单元,增加了热量消散的连通通道,可有效降低制动后制动盘的温度值和应力值,改善制动后制动盘散热效果.
