借作图手段 促深度思考

蔡燕清

[摘 要]高年级学生遇到的数学问题相比较之前更复杂难懂，这时是画图价值体现的最好时机。教师要让图形在繁杂的数量关系中显山露水，把抽象问题形象化、简单化，使学生体会图文“互译”的美妙，体现作图在解决问题中举足轻重的作用。

[关键词]作图;深度思考;思维能力

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）05-0010-02

虽然高年级学生已经具有一定的作图经验、技能及识图能力，也具有一定的抽象思维和逻辑推理能力，但他们大部分仍喜欢用所谓快捷、简单的公式和法则等解题，只是为做题而做题，缺乏深度思考，没能体会到“数形结合百般好”的真谛，长此以往，不利于学生的数学学习。本文利用一些经典习题来阐明如何借助作图促进高年级学生深度思考，从而提高他们的解题能力和数学素养。

一、利用成就动机，激发作图兴趣

美国哈佛大学教授麦克利兰认为，成就动机是一个个体追求自我价值的时候，通过方法达到最完美的状态。它是一种内在驱动力的体现，同时也能够直接影响人的行为活动、思维方式。学生遇到问题之所以不喜欢画图，是觉得画图是一种负担，没能把画图当作一种内在需求。因此，教师要深挖习题的思想性和延展性，让作图上升到解题的主导地位，促使学生通过作图解决问题，体验成功的快乐。

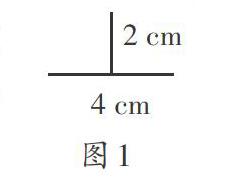
例如，教学人教版教材六年级下册“平面图形的面积复习课”时，教师设计了一道开放性习题：如图1，利用这两条线段能画出哪些图形？请画出后计算面积是多少。

学生通过粗画草图很快得到7个基本图形（如图2），并求出图形相应的面积。

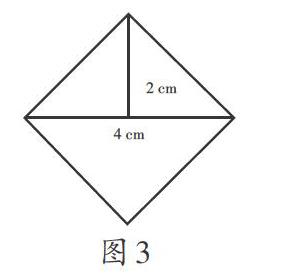
当学生为自己能画出这么多图形并计算出相应面积而沾沾自喜时，教师追问：“还有其他图形吗？”学生已是无计可施。这时教师适时引导学生观察三角形，并以手势为辅，学生顿悟，马上画出图3，并算出图形的面积为4×2÷2×2=8（cm2）。

此时教师继续启发学生看图思考：图3中的正方形的两条对角线跟正方形的面积有什么关系？学生经过思考得到4×4÷2=8（cm2），他们惊奇地发现正方形的面积=对角线×对角线÷2。温故时知新，这获得的是一种怎样的骄傲和愉悦。

有了这样的作图体验，学生找到了作图解题的乐趣，体会到作图解题的成就感，感受到作图的神奇。由此可见，教师要深挖习题的深度，让学生在作图中不断深入思考，让作图成为内驱力。

二、优选作图方式，提高解题能力

高年级学生经历了低、中年级利用实物图、色条图等数形结合解题的过程，已经进入高阶作图阶段——用线段图、数轴、正方形、圆等理解数和数量关系，升华到真正的“以形助数，化难为易”，在选择、辨析最优作图方式的过程中，思考力得到最大限度的提高。

例如，教学人教版教材六年级下册“正比例关系图像”后，笔者设计习题：王叔叔骑自行车从书店去银行花了4分钟，书店和银行之间的距离是600米，到达银行后马上用6分钟返回书店，同一时间李叔叔步行从银行去書店花了12分钟。（1）他们在途中第一次相遇用了几分钟？（2）他们在途中第二次相遇又用了几分钟？

学生有了两条线相交会有交点和正比例关系的作图经验，经过小组讨论得到解决方案：利用坐标轴来分析题中的数量关系（如图4）。

学生作完图后感觉一目了然：图中有两个交点，对应的时间分别是3分钟和8分钟，所以3分钟时他们第一次相遇，8分钟时他们第二次相遇。靠一张图就轻松解决了行程问题，学生感受到作图解决问题的直观和便捷，发自肺腑地感叹：“作图对解题真的起到了四两拨千斤的作用。”

三、对原图再创造，提高思考能力

利用图式让学生展开想象和思考，有利于学生创新品质的发展;目睹数在点和线之间的精彩演绎，亲历作图过程，学生就能感受到作图的魅力。

例如，学生画出图4后，教师让学生识图反思，进行再创造。

师：哪位同学能把图4再说一说？

生1：由图可知，书店和银行的距离是600米，王叔叔骑自行车从书店去银行用4分钟，2分钟行300米，可以看出，去时王叔叔所行路程和时间成正比例，他的速度是150米/分，到达后立即返回，用时6分钟，可知返回速度是600÷6=100（米/分），同时李叔叔从银行出发步行去书店用时12分钟，可知李叔叔步行速度是600÷12=50（米/分）。

生2：我还知道他们两人同时出发后经过3分钟在途中第一次相遇，经过8分钟在途中第二次相遇。

师：图中看到第一次相遇是3分钟 ，这3分钟的真正意义是什么？

生3：可以把图4转化为线段图，第（1）题就变成了求相遇时间的问题， 如图5。

生4：600÷（150+50）=3（分），所以图中两条线段相交的这个点对应的3分钟蕴含着“路程÷速度和=相遇时间”的数量关系。

师：第二次是在8分钟相遇，又蕴含什么道理？能用线段图把它们的数量关系表示出来吗？

（因为“相遇”一词的干扰，学生还是存在作图障碍;教师引导作图，如图6）

从再创造的线段图中，学生很快理解图4中第二次相遇时间8分钟蕴含追及问题中“追及时间=相差的路程÷速度差”的数量关系，同时从单条线段看出王叔叔到达银行，李叔叔已离开银行600÷150=4（分），也就是说李叔叔在王叔叔前4×50=200（米），所以第二次相遇时间即是王叔叔追上李叔叔的时间200÷（100-50）+4=8（分）。

学生从坐标图中识图之后创造出线段图，再在线段图的基础上进行抽象，总结出解题公式并熟练运用，这种“文字—图—脱图”的过程是学生思维剥茧抽丝的过程。由此可见，识图后把原图再创造，能加深对知识本质的理解，有利于思考能力的提升。

综上，教师应给予高年级学生作图的自主权，让学生根据实际选择合适的作图方式，自主构造，让作图帮助理解题意，真正发挥线段图的桥梁作用，使作图成为撬动学生主动思维的支点。

【本文系福建莆田市教育科学2020年度名师专项课题《基于启智数学的小学数学习题设计研究》（编号：PTMS20002）阶段性成果。】

（责编 金 铃）