“三数两差”帮你轻松做判断
2021-03-15魏先华
魏先华


平均数、中位数、众数、极差、方差(以下简称“三数两差”)是数据统计分析中的统计量,有着各自重要的意义。弄清“三数两差”的概念和意义,可以帮你轻松解决相关的问题。
一、根据概念做判断
例1 (2020·江苏无锡)已知一组数据:21,23,25,25,26,这组数据的平均数和中位数分别是( )。
A.24,25 B.24,24
C.25,24 D.25,25
【解析】这组数据的平均数是(21+23+25+25+26)÷5=24;把这组数据从小到大排列为:21,23,25,25,26,最中间的数是25,则中位数是25。
故选A。
【点评】本题考查的是平均数和中位数的概念。确定一组数据的中位数可以分两步进行:一排序,二取中。
例2 (2020·江苏南通)一组数据2,4,6,x,3,9的众数是3,则这组数据的中位数是( )。
A.3 B.3.5 C.4 D.4.5
【解析】∵这组数据2,4,6,x,3,9 的众数是3,
∴x=3,
从小到大排列这组数据为:2,3,3,4,6,9,处于中间位置的两个数是3和4,
∴这组数据的中位数是(3+4)÷2=3.5。
故选B。
【点评】本题考查的是众数和中位数的概念。同学们需要先根据众数的概念确定x 的值,然后再根据中位数的概念确定中位数。例3 (2020·江苏徐州)小红连续5天的体温数据如下(单位:℃):36.6,36.2,36.5,36.2,36.3。关于这组数据,下列说法正确的是( )。
A.中位数是36.5℃
B.众数是36.2℃
C.平均數是36.2℃
D.极差是0.3℃
【解析】A.把小红连续5天的体温从小到大排列为:36.2,36.2,36.3,36.5,36.6,处在中间位置的一个数是36.3,因此中位数是36.3℃,所以此选项错误;
B.出现次数最多的是36.2℃,因此众数是36.2℃,所以此选项正确;
C. 平均数为-x=(36.2+36.2+36.3+36.5+36.6)÷5=36.36℃,所以此选项错误;
D.极差是一组数据中的最大值与最小值的差,即为36.6-36.2=0.4℃,所以此选项错误。故选B。
【点评】本题考查的是中位数、众数、平均数、极差的概念。同学们在计算过程中只要细心就能不出错。
二、结合意义做判断
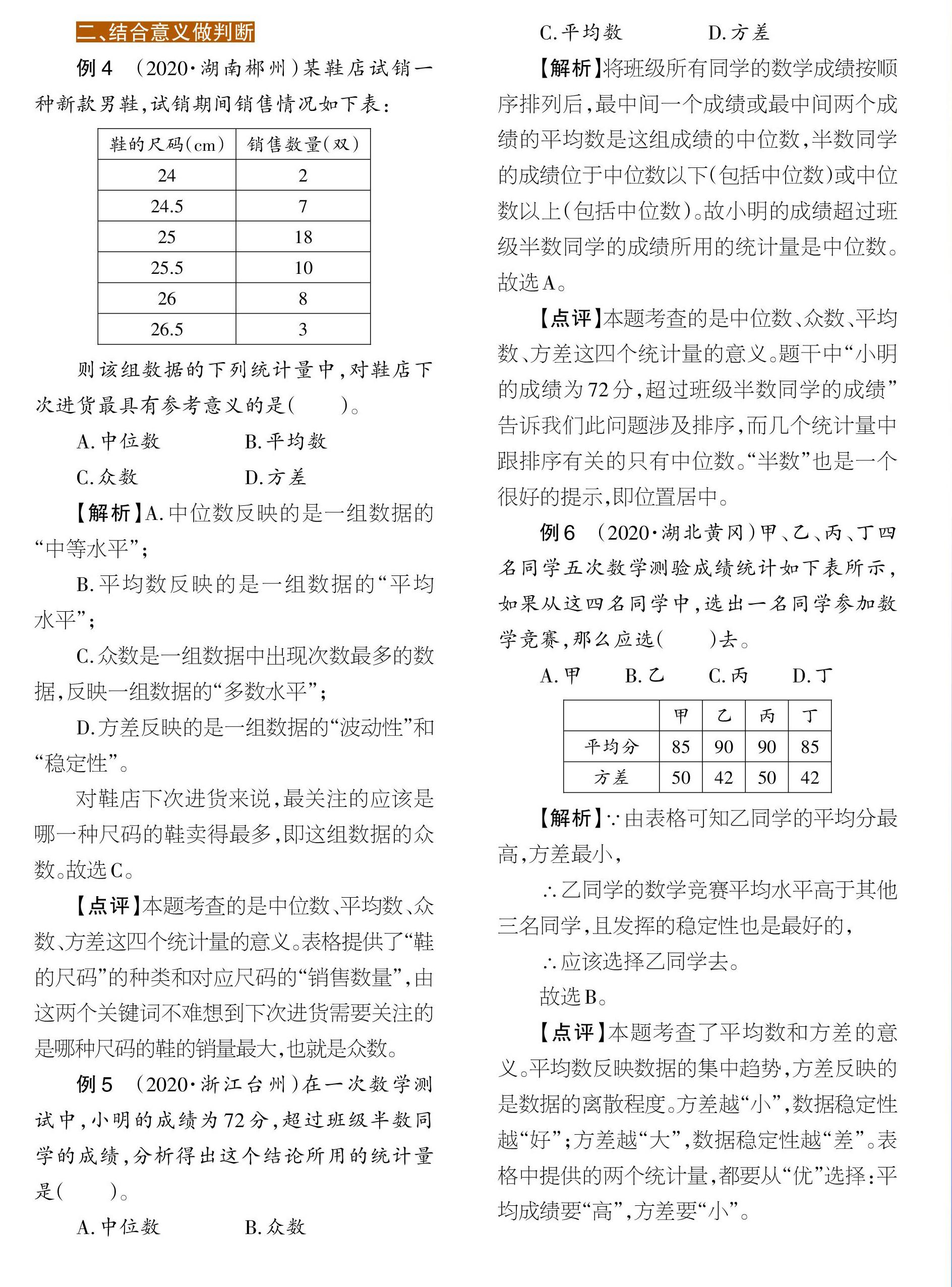
例4 (2020·湖南郴州)某鞋店试销一种新款男鞋,试销期间销售情况如下表:
则该组数据的下列统计量中,对鞋店下次进货最具有参考意义的是( )。
A.中位数 B.平均数
C.众数 D.方差
【解析】A.中位数反映的是一组数据的“中等水平”;
B. 平均数反映的是一组数据的“平均水平”;
C.众数是一组数据中出现次数最多的数据,反映一组数据的“多数水平”;
D.方差反映的是一组数据的“波动性”和“稳定性”。
对鞋店下次进货来说,最关注的应该是哪一种尺码的鞋卖得最多,即这组数据的众数。故选C。
【点评】本题考查的是中位数、平均数、众数、方差这四个统计量的意义。表格提供了“鞋的尺码”的种类和对应尺码的“销售数量”,由这两个关键词不难想到下次进货需要关注的是哪种尺码的鞋的销量最大,也就是众数。
例5 (2020·浙江台州)在一次数学测试中,小明的成绩为72分,超过班级半数同学的成绩,分析得出这个结论所用的统计量是( )。
A.中位数 B.众数
C.平均数 D.方差
【解析】将班级所有同学的数学成绩按顺序排列后,最中间一个成绩或最中间两个成绩的平均数是这组成绩的中位数,半数同学的成绩位于中位数以下(包括中位数)或中位数以上(包括中位数)。故小明的成绩超过班级半数同学的成绩所用的统计量是中位数。
故选A。
【点评】本题考查的是中位数、众数、平均数、方差这四个统计量的意义。题干中“小明的成绩为72分,超过班级半数同学的成绩”告诉我们此问题涉及排序,而几个统计量中跟排序有关的只有中位数。“半数”也是一个很好的提示,即位置居中。
例6 (2020·湖北黄冈)甲、乙、丙、丁四名同学五次数学测验成绩统计如下表所示,如果从这四名同学中,选出一名同学参加数学竞赛,那么应选( )去。
A.甲 B.乙 C.丙 D.丁
【解析】∵由表格可知乙同学的平均分最高,方差最小,
∴乙同学的数学竞赛平均水平高于其他三名同学,且发挥的稳定性也是最好的,
∴应该选择乙同学去。
故选B。
【点评】本题考查了平均数和方差的意义。平均数反映数据的集中趋势,方差反映的是数据的离散程度。方差越“小”,数据稳定性越“好”;方差越“大”,数据稳定性越“差”。表格中提供的两个统计量,都要从“优”选择:平均成绩要“高”,方差要“小”。
三、结合统计图做判断
例7 (2020·江苏泰州)2020年6月6日是第25个全国爱眼日,某校从八年级随机抽取50名学生进行了视力调查,并根据视力值绘制成统计图(如图1),这50名学生视力的中位数所在范围是。
【解析】∵一共调查了50名学生的视力情况,
∴这50个数据的中位数是第25个和第26个数据的平均数,由统计图可知第25个和第26个数据都落在4.65—4.95之间,
∴这50名学生视力的中位数所在范围是4.65—4.95。
故答案为4.65—4.95。
【点评】本题考查了根据图表信息确定中位数的方法。同学们需要先了解中位数的概念,再结合统计图得到相关的信息,最后才能解决问题。
例8 (2020·湖北咸宁)如图2是甲、乙两名射击运动员某节训练课的5次射击成绩的折线统计图,下列判断正确的是( )。
A.乙的最好成绩比甲高
B.乙的成绩的平均数比甲小
C.乙的成绩的中位数比甲小
D.乙的成绩比甲稳定
【解析】A.由折线统计图可知:甲运动员的成绩为6、7、10、8、9,乙运动员的成绩为8、9、8、7、8,甲的最好成绩为10环,乙的最好成绩为9环,所以此选项错误;
B.甲的成绩的平均数为(6+7+10+8+9)÷5=8,乙的成绩的平均数为(8+9+8+7+8)÷5=8,两者一样大,所以此选项错误;
C.甲的成绩的中位数为8,乙的成绩的中位数为8,两者一样大,所以此选项错误;
D.甲的成绩的方差为15[(6-8)2 +(7-8)2 +(8-8)2+(9-8)2+(10-8)2]=2,乙的成绩的方差为15[(8-8)2 +(9-8)2 +(8-8)2+(7-8)2+(8-8)2]=0.4,0.4<2,所以乙的成绩比甲稳定,所以此选项正确。
故选D。
【点评】本题考查了同学们的读图能力以及平均数、中位数、方差的计算方法。同学们可以由折线统计图得出甲和乙两名运动员五次射击的具体成绩,然后分别计算出平均数、中位数、方差,再作出比较。对于甲和乙的方差比较,本题其实也可以由甲和乙的折线统计图得出乙的折线图要比甲的折线图波动性小,所以乙的成绩稳定性更好。
(作者单位:江苏省盐城市神州路初级中学)
