口诀突破统计与概率

第八章统计和概率的简单应用领衔人：卞书彦组稿团队：江苏省盐城市盐都区数学教师发展共同体

统计与概率是初中数学的一个重要组成部分，与人们的生产与生活密切相关，也是中考必考知识点。下面我们利用口诀来解决有关数据的收集与整理、数据的分析以及概率的简单应用等问题。

一、数据的收集与整理

例1 （2020·广西）以下调查中，最适合采用全面调查的是（ ）。

A.检测长征运载火箭的零部件质量情况

B.了解全国中小学生课外阅读情况

C.调查某批次汽车的抗撞击能力

D.检测某城市的空气质量

解：A。

【点评】本题考查全面调查、抽样调查的意义。当调查的工作量不太大或者要求精度准确时，一般采用普查;当调查工作量比较大，普查本身无法完成，或者调查具有破坏性时，宜采用抽查。抽查时选择的样本还要具有代表性和广泛性。

例2 （2020·黑龙江大庆）为了了解某校某年级1000名学生一分钟的跳绳次数，从中随机抽取了40名学生的一分钟跳绳次数（次数为整数，且最高次数不超过150 次），整理后绘制成如图的频数直方图，图中的a、b 满足关系式2a=3b。后由于保存不当，部分原始数据模糊不清，但已知缺失数据都大于120。

请结合所给条件，回答下列问题：

（1）求问题中的总体和样本容量;

（2）求a、b 的值（请写出必要的计算过程）;

（3）如果一分钟跳绳次数在125次以上（不含125次）为跳绳成绩优秀，那么该校该年级学生跳绳成绩优秀的人数大约是多少？（注：该年级共1000名学生）

解：（1）总体是某校某年级1000名学生一分钟的跳绳次数，样本容量是40。

（2）由题意所给数据可知：50.5～75.5 的有4人，75.5～100.5的有16人，

∴a+b=40-4-16=20。

∵2a=3b，

∴解得a=12，b=8。

（3）1000× 840=200（人）。

答：该校该年级学生跳绳成绩优秀的大约是200人。

【点评】统计里，所考察对象的全体叫作总体，组成总体的每一个考察对象叫作个体，从总体中所抽取的一部分个体叫作总体的一个样本，样本中个体的数目叫作样本容量。某个对象出现的次数称为频数，频数与总次数的比值称为频率。其中，各组频数之和等于样本容量（总次数），各组频率之和等于1。我们要会用抽取的样本具有的特征来估计总体具有的特征。故我们总结为：

调查分普抽，抽样具有代表性，

总体和样本，两频之间关系明，

频数和为总，频率之和总为1。

二、数据的分析

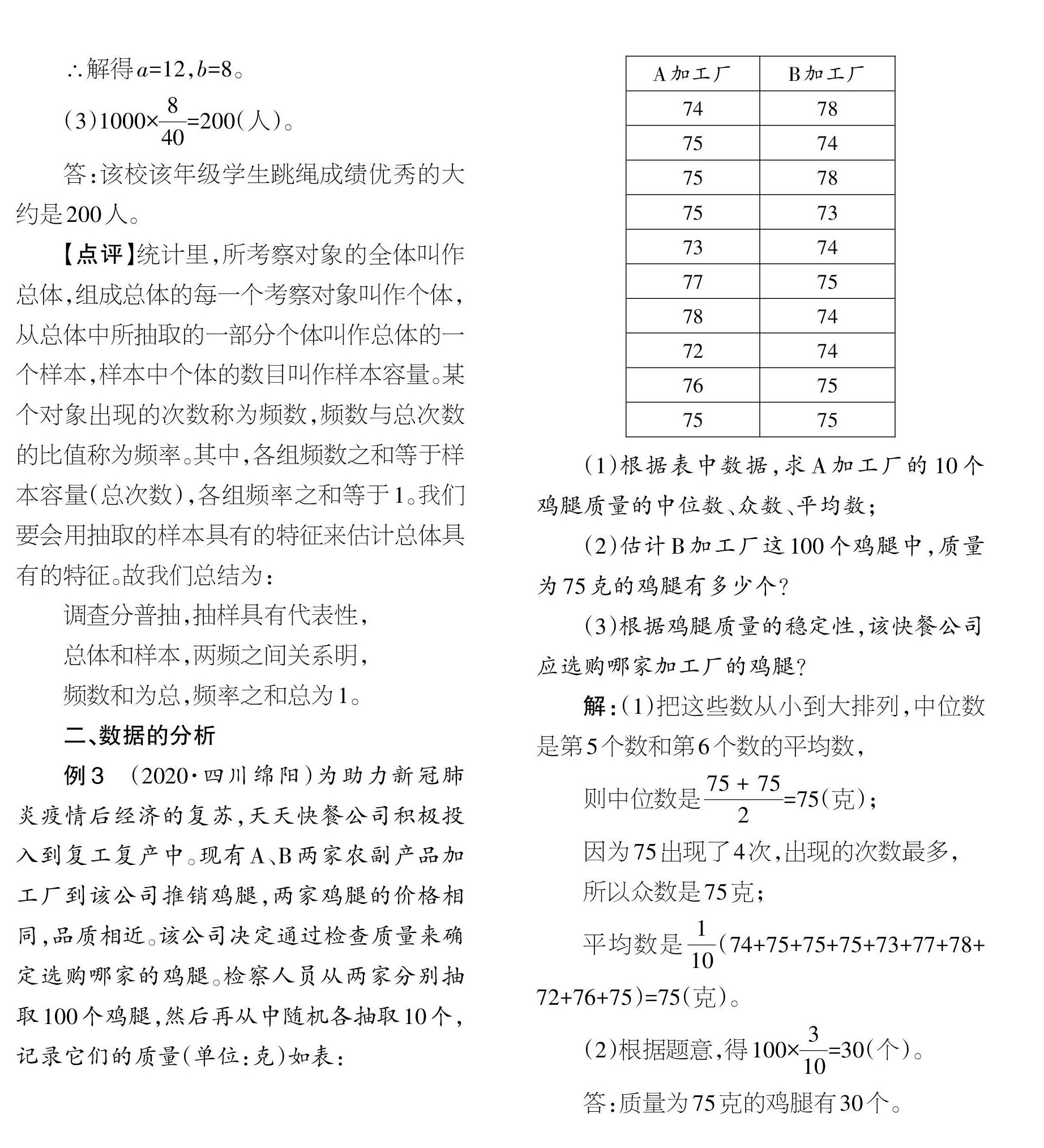
例3 （2020·四川綿阳）为助力新冠肺炎疫情后经济的复苏，天天快餐公司积极投入到复工复产中。现有A、B两家农副产品加工厂到该公司推销鸡腿，两家鸡腿的价格相同，品质相近。该公司决定通过检查质量来确定选购哪家的鸡腿。检察人员从两家分别抽取100个鸡腿，然后再从中随机各抽取10个，记录它们的质量（单位：克）如表：

（1）根据表中数据，求A 加工厂的10 个鸡腿质量的中位数、众数、平均数;

（2）估计B加工厂这100个鸡腿中，质量为75克的鸡腿有多少个？

（3）根据鸡腿质量的稳定性，该快餐公司应选购哪家加工厂的鸡腿？

解：（1）把这些数从小到大排列，中位数是第5个数和第6个数的平均数，

则中位数是75 + 752 =75（克）;

因为75出现了4次，出现的次数最多，

所以众数是75克;

平均数是110（74+75+75+75+73+77+78+72+76+75）=75（克）。（2）根据题意，得100× 310=30（个）。

答：质量为75克的鸡腿有30个。

（3）选B加工厂的鸡腿。

A 的方差是110[（74-75）2+4×（75-75）2+（76-75）2+（73-75）2+（72-75）2+（77-75）2+（78-75）2]=2.8。

B的平均数是110（78+74+78+73+74+75+74+74+75+75）=75，

B的方差是110[2×（78-75）2+4×（74-75）2+（73-75）2+3×（75-75）2]=2.6。

∵A、B 平均值一样，B 的方差比A 的方差小，B更稳定，

∴选B加工厂的鸡腿。

【点评】如果一组数据中所有数据的大小差异不大，那么平均数就能较好地反映这组数据的集中趋势。如果一组数据中的个别数据与其他数据的大小差异很大，那么平均数就不能很准确地反映这组数据的集中趋势，此时常采用中位数或众数描述这组数据的集中程度。而在描述数据的稳定性时主要看两差：极差与方差。极差是一组数据中最大值与最小值的差，能反映这组数据的变化范围;方差公式为s2=1n

[（x1-x）2+（x2-x）2+…+（xn-x）2]，一般说来，一组数据的方差越小，这组数据的离散程度就越小，这组数据就越稳定。

因此我们总结为：集中三数据，极端宜用中或众，离散看两差，方差值小而稳定。

例4 （2020·内蒙古呼伦贝尔）某校为了了解初中学生每天的睡眠时间（单位为小时），随机调查了该校的部分初中学生，根据调查结果，绘制出如图统计图。

请根据相关信息，解答下列问题：

（1）本次接受调查的初中学生人数为人，扇形统计图中的m= ，条形统计图中的n= ;

（2）所调查的初中学生每天睡眠时间的众数是，方差是;

（3）该校共有1600名初中学生，根据样本数据，估计该校初中学生每天睡眠时间不足8小时的人数。

解：（1）本次接受调查的初中学生有4÷10%=40（人），

m%=10÷40×100%=25%，

n=40×37.5%=15。

故答案为40，25，15。

（2）由条形统计图，可得众数是7，

x= 1

40×（5×4+6×8+7×15+8×10+9×3）=7，

s2= 1

40[（5-7）2×4+（6-7）2×8+（7-7）2×15+（8-7）2×10+（9-7）2×3]=1.15。

故答案为7，1.15。

（3）1600× 4 + 8 + 1540 =1080（人）。

即该校初中学生每天睡眠时间不足8小时的有1080人。

【点评】常用的统计图有条形统计图、折线统计图、扇形统计图以及频数分布直方图。条形统计图能清楚地描述各统计项目的数据;折线统计图能清楚地描述数据的变化过程和趋势;扇形统计图能清楚地描述各统计项目占总体的百分比;频数分布直方图用横轴表示考察对象数据的变化范围，用纵轴表示相应范围内数据的频数。

一般地，考题会用缺一些数据的两个及以上图表来设置，这就需要我们对照这些图表找出它们之间的对应关系，来解决有关问题，故曰：

统计有四图，互相照应提信息，分量求总量，量率对应除得全。

三、简单概率

例5 （2020·内蒙古呼伦贝尔）一个不透明的口袋中装有三个完全相同的小球，上面分别标有数字2， 3，5。

（1）从口袋中随机摸出一个小球，求摸出小球上的数字是无理数的概率（直接写出结果）。

（2）先从口袋中随机摸出一个小球，将小球上的数字记为x，把小球放回口袋中并搅匀，再从口袋中随机摸出一个小球，将小球上的数字记为y。请用列表法或画树状图法求出x 与y 的乘积是有理数的概率。

解：（1）摸出小球上的数字是无理数的概率为23。

（2）画树状图如下：共有9种等可能的结果，其中两个数字的乘积为有理数的有3种，

∴两次摸出的小球所标数字的乘积是有理数的概率为39=13。

【点评】此题考查的是用列表法或树状图法求概率。列表法可以不重复不遗漏地列出所有等可能的结果，适合于两步完成的事件;树状图法适合两步或两步以上完成的事件。解题时要注意此题是放回实验还是不放回实验。用到的知识点为：概率=所求情况数与总情况数之比。

例6 （2020·山东威海）小伟和小梅两名同学玩掷骰子的游戏，两人各掷一次均匀的骰子。以掷出的点数之差的绝对值判断输赢。若所得数值等于0、1、2，则小伟胜;若所得数值等于3、4、5，则小梅胜。

（1）请利用表格分别求出小伟、小梅获胜的概率。

（2）判断上述游戏是否公平。如果公平，请说明理由;如果不公平，请利用表格修改游戏规则，以确保游戏的公平性。

解：（1）用列表法表示所有可能出现的结果如下：

表中共有36种可能的结果，每一种结果出现的可能性相同，“差的绝对值”为0、1、2的共有24种，“差的绝对值”为3、4、5的共有12种，

所以P（小伟胜）=

，

P（小梅胜）=

。

答：小伟获胜的概率为23，小梅获胜的概率为13。

（2）∵23≠13，∴游戏不公平。

根据表格中“差的绝对值”的不同情况，要使游戏公平，则两人获胜的概率相等。于是修改为：两次掷的点数之差的绝对值为1，2，则小伟胜;否则小梅胜。这样小伟、小梅获胜的概率均为12。（规则修改不唯一）

【点评】当列举的可能结果比较多时，我们可采用列表法来解决。本题还考查了游戏的公平性。列举出所有的可能结果，求出相应的概率是解决问题的关键。我们在修改游戏规则时，一般使得游戏所分对象中包含的可能性结果一样多，有时也采用赋分制修改游戏规则，但一般不改变游戏具体方式。

例7 （2020·江苏徐州）在一个不透明的袋子里装有红球、黄球共20个，这些球除顏色外都相同。小明通过多次试验发现，摸出红球的频率稳定在0.25左右，则袋子中红球的个数最有可能是（ ）。

A.5 B.10 C.12 D.15

解：A。

【点评】本题主要考查了利用频率估计概率。大量重复试验时，事件发生的频率在某个固定位置左右摆动，并且摆动的幅度越来越小，根据这个频率稳定性，可以用频率的集中趋势来估计概率，这个固定的近似值就是这个事件的概率。

我们在解决概率有关问题时，采用：

概率树与表，分清放回不放回，

事件两三步，三步须用树状图，

试验等可能，多次频率估概率。

（作者单位：江苏省盐城市大冈初级中学）98 策略方法