你会解“非直角”三角形吗？

周炼

在“锐角三角函数”这一章中，同学们通过学习，大多可以掌握解直角三角形的方法，但如果题目中的三角形不是直角三角形，而是锐角三角形或钝角三角形，你还能根据其中的一些条件求出其他元素吗？解“非直角”三角形有哪些情形？它们与解直角三角形之间又有怎样的联系呢？

一、“两边一角”型

例1 如图1，在△ABC中，∠A为钝角，AB=25，AC=39，sinB=3/5，求tanC和BC的长。

【解析】这道题给出了三角形的其中两条边和一个锐角的三角函数值，但这些条件都不在直角三角形中，而是在一个钝角三角形中，要想将它们用起来，就要通过作辅助线给AB、AC、∠B、∠C都找到属于自己的直角三角形。通过分析我们发现，如果过点A作AD⊥BC于点D（如图2），那么在Rt△ADB中，由sinB=AD/AB=3/5，可以求出AD=15，再由勾股定理得出BD=

。在Rt△ADC中，同样由勾股定理可以得到

，从

，BC= BD+CD=20+3 6=56。

二、“两角一边”型

例2 如图3，在△ABC中，∠A=120°，∠C=45°，AB=2，求AC的長。

【解析】可能同学们看到∠A =120°这一条件会觉得无从下手，因为1200的角是钝角，其三角函数值已经超出了我们目前所学的内容。那么，如何对这一条件进行合理的转化呢？联系七年级学过的角的相关知识，不难想到虽然120°的角是钝角，但是其补角60°却是锐角，所以只要作出BA或者CA的延长线就可以将120°转为60°使用，但是到底延长哪一条边依然值得思考。这道题给出的条件是三角形中两个角的度数和一条边长，我们发现如果要同时构造关于∠A的补角，∠C以及边AB的直角三角形，只能延长CA，并过点B作CA延长线的垂线交于点D（如图4），根据锐角三角函数的定义以及特殊角的三角函数值，在Rt△ADB中可以求出AD=1，BD=3，在Rt△CDB中可以求出CD=3，从而AC=CD-AD=3-1。

三、“三边”型

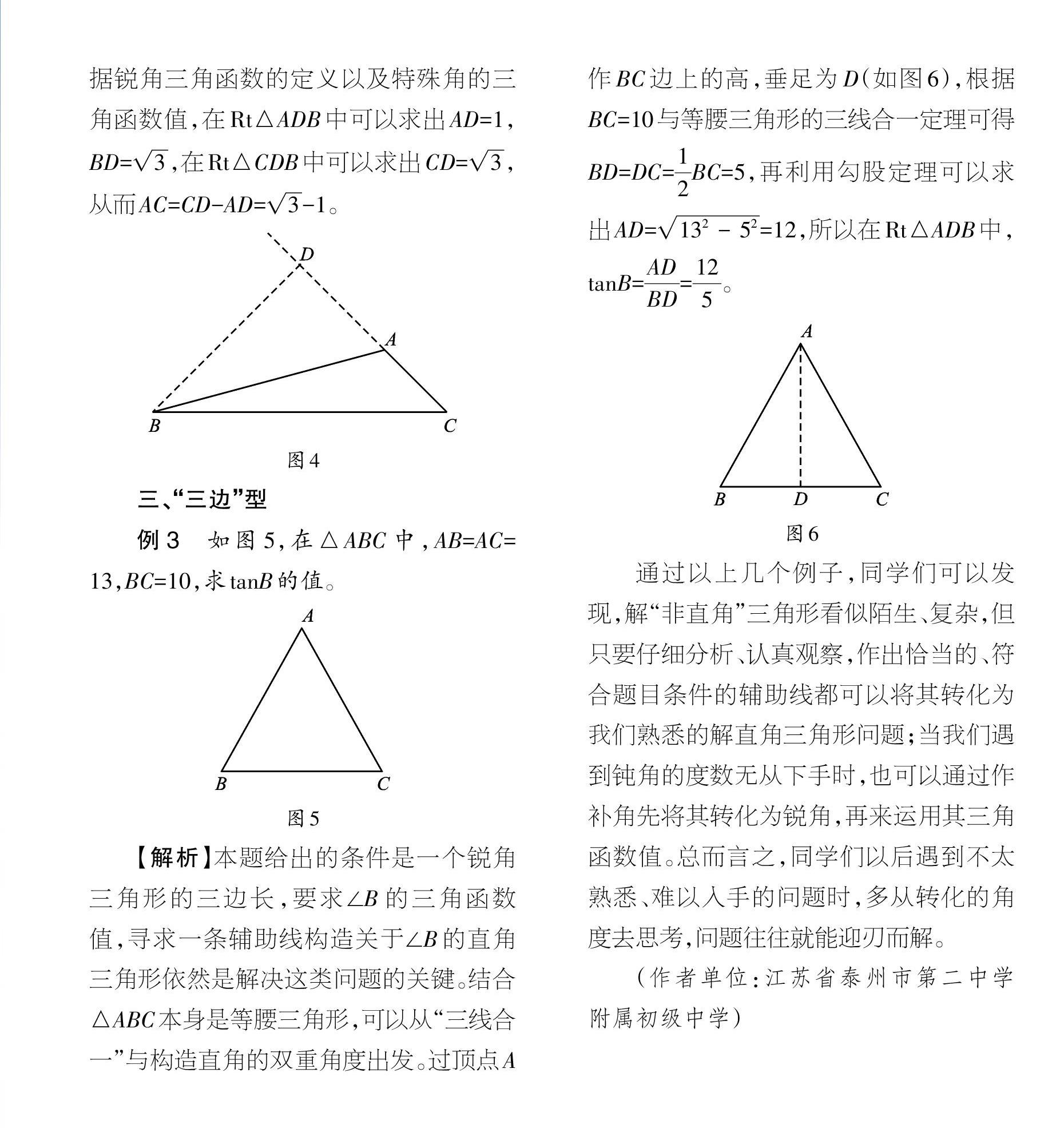
例3 如图5，在△ABC中，AB=AC=13，BC=10，求tanB的值。

【解析】本题给出的条件是一个锐角三角形的三边长，要求∠B的三角函数值，寻求一条辅助线构造关于∠B的直角三角形依然是解决这类问题的关键。结合△ABC本身是等腰三角形，可以从“三线合一”与构造直角的双重角度出发。过顶点A作BC边上的高，垂足为D（如图6），根据BC=10与等腰三角形的三线合一定理可得BD=DC=1/2BC=5，再利用勾股定理可以求出

，所以在Rt△ADB中，

。

通过以上几个例子，同学们可以发现，解“非直角”三角形看似陌生、复杂，但只要仔细分析、认真观察，作出恰当的、符合题目条件的辅助线都可以将其转化为我们熟悉的解直角三角形问题;当我们遇到钝角的度数无从下手时，也可以通过作补角先将其转化为锐角，再来运用其三角函数值。总而言之，同学们以后遇到不太熟悉、难以人手的问题时，多从转化的角度去思考，问题往往就能迎刃而解。

（作者单位：江苏省泰州市第二中学附属初级中学）