BeB+离子基态及激发态的势能函数与跃迁性质

袁 娣， 万明杰， 黄多辉

（1.宜宾学院计算物理四川省高校重点实验室，四川宜宾644007； 2.宜宾学院物理与电子工程学院，四川宜宾644007）

Be作为最轻的碱土金属元素被广泛地应用于制造轻便硬质合金.Be合金具有独特的物理化学性质，在太空、核工业等不同的领域中得到广泛地应用［1］.BeB是在20世纪90年代才被发现的，它具有化学性质稳定，低密度、高硬度、高声速的特点，这些特性使得BeB在火箭推进剂［2-3］、空间结构和光学镜中具有非常大的吸引力，引起了研究者的广泛关注.1994年，Boldyrev等［4］首次进行对BeB的电子结构从头计算研究，得出5个低电子态的电子结构和光谱常数.同年，Ornellas等［5］利用多参考双组态相互作用（MRSDCI）方法计算了BeB的20个低激发态的势能曲线和17个低激发态的偶极矩函数，他们利用获得的势能曲线（PECs）测定了13种低能态的电子结构和光谱性质.2003年，Pelegrini等［6］利用MRSDCI方法计算了BeB的Χ2Π和Α2Σ+态的势能函数、偶极矩和跃迁偶极矩，并确定这2个态的光谱常数、跃迁概率和辐射寿命.2018年，Zhou等［7］利用考虑Davidson修正的内收缩多参考组态相互作用（icMRCI+Q）的方法研究了16个低电子态的光谱常数、跃迁偶极矩和跃迁概率.经过前人的努力，对BeB分子的电子结构和光谱性质有了普遍的研究.但是到目前为止，实验上和理论上对BeB+离子的光谱性质和跃迁性质报道很少.研究正离子的电子结构和光谱性质可以帮助我们理解发生在彗尾、恒星大气和星际空间之间的物理化学过程，而且正离子还可以作为燃烧过程中研究化学动力学的监测探针［8］.BeB+离子是等离子体物理学和天体物理学研究领域里很重要的分子之一.因此，对于BeB+离子的研究尤为重要.为了进一步对BeB+离子的研究提供理论参数，本文着重计算了BeB+离子前3个离解通道对应的7个Λ-S态的势能曲线、光谱常数和跃迁性质.

1 计算方法

BeB+离子7个Λ-S态的电子结构是采用Werner等［9］开发的量子化从头算MOLPRO 2010程序包完成的.由于MOLPRO程序的限制性，本文计算时把对称性降到了C2v子群中.在核间距R＝0.08～3.0 nm范围内对BeB+离子进行了单点能计算，计算步长为0.01 nm，为了使得到的势能曲线的数据更加平滑，在平衡位置Re附近，步长选取为0.001 nm.在计算时，首先采用Hartree-Fock（HF）自洽场方法得到BeB+离子基态的初始猜测分子轨道和波函数，接着采用在完全活性空间自洽场中通过自动改变态的平均权重的动态权重方法（CASSCF）［10-11］来进行轨道优化得到多参考波函数，然后考虑Davidson修正的内收缩多参考组态相互作用（MRCI+Q）［12-15］方法计算BeB+离子7个Λ-S态的势能曲线.为了提高这些态的势能曲线的精度，对Be和B都采用了Dunning相关调和基函数并含扩散基的大基组aug-cc-pV5Z［16-18］.在CASSCF方法及MRCI方法计算过程中，Be的1s2s轨道为双占据的闭壳层轨道，Be的2p3s3p和B的1s2s2p轨道为活性轨道，记为CAS（4，12）.最后，采用M-S函数拟合得到每个电子态的光谱常数并利用Level 8.0［19］程序对各个电子态的爱因斯坦辐射系数Av′v″、弗兰克-康登因子f v′v″、总辐射速率Atotal和自发辐射寿命τ进行了预测.

2 结果与讨论

2.1 势能曲线及离解极限为了准确表达BeB+离子的势能函数，必须确定可能的电子态和合理的离解极限［20-21］.由于Be原子和B原子的基态电离能分别是75 192.64和66 928.04 cm-1［22］.因此，BeB+离子的第一离解通道为Be（1Sg）+B+（1Sg）.又因为Be原子和B原子第一激发态的能级分别为21 978.28和28 870.0 cm-1［22］，Be+和B+第一激发态的能级分别为31 928.744和37 335.54 cm-1［22］，所以BeB+离子第二离解通道为Be+（2Sg）+B（2Pu）、第三离解通道为Βe（3Pu）+Β+（1Sg）.根据原子分子反应静力学原理和Wigner-Witmer定则［23-24］，可以推算出第一个离解通道对应的BeB+离子的基态Χ1Σ+.本文采用MRCI+Q方法得到的BeB+离子前3个离解通道对应的7个Λ-S态的势能曲线如图1所示，基态Χ1Σ+的势能曲线具有稳定结构的极小点，表明BeB+离子的基态能稳定存在.第二个离解通道对应电子态a3Π、13Σ+、A1Π、B1Σ+，其中a3Π、13Σ+、A1Π的势能曲线均具有对应离子稳定结构的极小点，表明这3个激发态都能稳定存在.由于B1Σ+电子态与更高的C1Σ+电子态存在避免交叉，使得B1Σ+电子态具有了双势阱结构［25］，这说明对称性相同的2个电子态之间存在比较强的相互作用.为了得到准确的结果，对这2个电子态都进行了优化计算.第三个离解通道对应电子态23Π和33Σ+，其中23Π电子态的势能曲线也具有对应的稳定结构极小点，所以23Π电子态能稳定存在.33Σ+电子态也与更高的3Σ+电子态存在避免交叉现象，所以也具有了双势阱结构.计算结果和理论推导是相一致的，说明我们计算的势能函数是正确的.

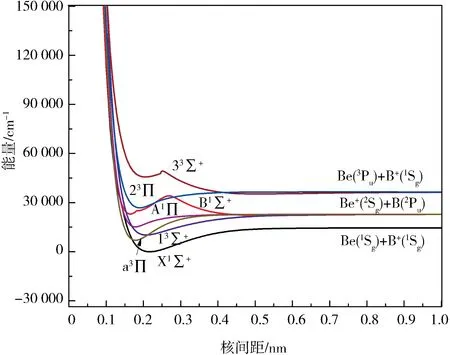
图1 BeB+离子7个电子态的势能曲线Fig.1 Potential energy curves for seven states of BeB+

下面计算3个离解通道之间的能量差来进一步验证计算结果的正确性，其结果见表1.前2个离解通道之间的能量差为8 266.03 cm-1，与实验值相差1.43 cm-1，相对误差仅为0.02%；第三个离解通道与第一个离解通道之间的能量差为21 871.53 cm-1，与实验值相差106.75 cm-1，相对误差仅为0.4%.可以看出，本文的离解极限能量差计算结果与实验值符合的很好，由此可以相信我们的计算结果是可靠的.

表1 BeB+离子分子态与原子态的离解关系Tab.1 Dissociation relationships between molecular states and atomic states of BeB+

2.2 光谱常数利用Level 8.0程序对BeB+离子7个Λ-S态的势能曲线进行拟合得到的光谱常数见表2.计算的BeB+离子的基态Χ1Σ+的平衡核间距Re＝0.217 0 nm，在平衡位置处其主要电子组态为1σ22σ23σ24σ2、权重为74.33%，次电子组态为1σ22σ23σ24σα5σβ、权重为9.31%.预测的势阱深度为1.814 3 eV，势阱能够支持61个振动态.

第一激发态a3Π和第二激发态13Σ+是来自第二离解通道的三重态，都是典型的束缚态.势阱深度分别为1.961 5和1.569 7 eV，势阱能够分别支持34个和69个振动态.a3Π在平衡位置Re＝0.178 9 nm处的主要电子组态为1σ22σ23σ24σα1πα，权重为89.41%，它主要来自于Χ1Σ+基态4σα→1πα的单电子激发，其绝热激发能Te＝7 019.903 5 cm-1.13Σ+在平衡位置Re＝0.207 4 nm处的主要电子组态为1σ22σ23σ24σα5σα，权重为91.73%，它主要来自于Χ1Σ+基态4σα→5σα的单电子激发，其绝热激发能Te＝10 239.139 2 cm1.

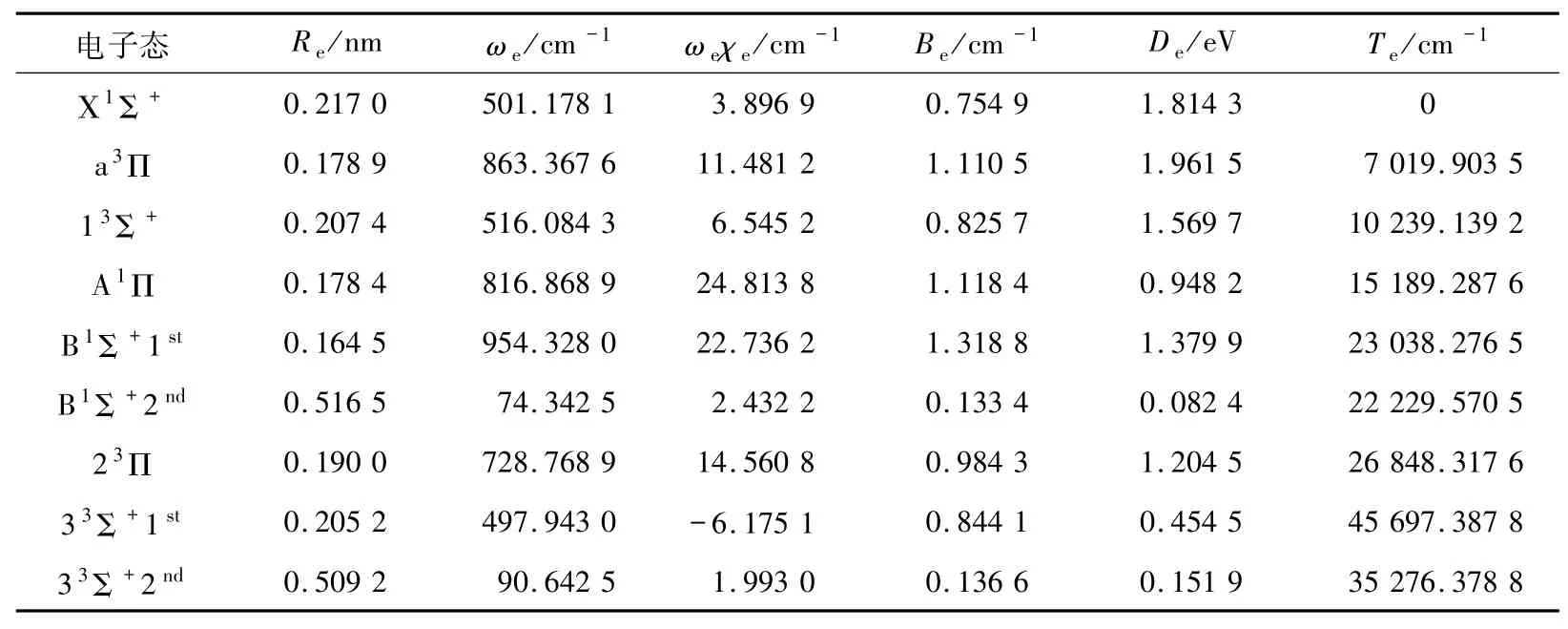
表2 BeB+离子7个电子态的光谱常数Tab.2 Spectroscopic constants of seven states of BeB+

第三激发态A1Π和第四激发态B1Σ+是来自第二离解通道的一重态.A1Π是典型的束缚态，势阱深度为0.948 2 eV，势阱能够支持22个振动态.在平衡位置Re＝0.178 4 nm处的主要电子组态为1σ22σ23σ24σα1πβ，权重为84.99%，它主要来自于Χ1Σ+基态4σβ→1πβ的单电子激发，其绝热激发能Te＝15 189.287 6 cm-1.B1Σ+是具有双势阱结构的电子态，在0.268 nm左右发生预解离.这是由于B1Σ+和更高的1Σ+电子态在该位置发生了避免交叉的现象.第一势阱深度为1.379 9 eV，势阱能够支持15个振动态.在平衡位置Re＝0.164 5 nm处的主要电子组态为1σ22σ23σ21πα和1σ22σ23σ21πβ，权重均为44.53%，它主要来自于Χ1Σ+基态4σα→1πα和4σβ→1πβ的单电子激发，其绝热激发能Te＝23 038.276 5 cm-1.第二势阱深度为0.082 4 eV，势阱能够支持27个振动态.在平衡位置Re＝0.516 5 nm处的主要电子组态为1σ22σ23σ24σα5σβ，权重为80.17%，它主要来自于Χ1Σ+基态4σβ→5σβ的单电子激发，其绝热激发能Te＝22 229.570 5 cm-1.

第五激发态23Π和第六激发态33Σ+是来自第三离解通道的三重态.23Π是典型的束缚态，势阱深度为1.204 5 eV，势阱能够支持28个振动态.在平衡位置Re＝0.190 0 nm处的主要电子组态为1σ22σ23σ25σα1πα，权重为78.96%，它主要来自于Χ1Σ+基态4σ→5σ和4σ→1π的双电子激发，其绝热激发能Te＝26 848.317 6 cm-1.33Σ+具有双势阱结构的电子态，在0.254 nm左右发生预解离.第一势阱深度为0.454 5 eV，势阱能够支持5个振动态.在平衡位置Re＝0.205 2 nm处的主要电子组态为1σ22σ23σ21πα2πα和1σ22σ23σ21πβ2πβ，权重分别为39.75%和39.74%，它主要来自于Χ1Σ+基态4σα→1πα、4σα→2πα和4σβ→1πβ、4σβ→2πβ的多电子激发，其绝热激发能Te＝45 697.387 8 cm-1.第二势阱深度为0.151 9 eV，势阱能够支持41个振动态.在平衡位置Re＝0.509 2 nm处的主要电子组态为1σ22σ23σ24σα6σα，权重为85.83%，它主要来自于Χ1Σ+基态4σα→6σα的单电子激发，其绝热激发能Te＝35 276.378 8 cm-1.

2.3 偶极矩和跃迁偶极矩偶极矩可以反应分子的成键性质，所以对BeB+离子7个Λ-S态的电偶极矩进行了理论计算.偶极矩是关于核间距的函数，其随核间距变化的曲线见图2.Χ1Σ+、a3Π、13Σ+、A1Π和23Π这5个电子态在平衡位置Re处的电偶极矩分别为0.861 2、1.643 1、-0.335 7、1.375 5和-0.314 9 a.u..B1Σ+和33Σ+由于避免交叉，他们的势能曲线都有2个势阱.他们的电偶极矩在2个势阱处的值分别为1.056 6、4.579 5、0.677 5和-3.701 5 a.u..值得一提的是，a3Π、13Σ+、A1Π、B1Σ+这4个电子态和Χ1Σ+、23Π、33Σ+这3个电子态的电偶极矩函数分别趋向于一个非零的数值，这是因为a3Π、13Σ+、A1Π、B1Σ+这4个电子态与离解极限Be++B相对应，Χ1Σ+、23Π、33Σ+这3个电子态均与离解极限Be+B+相对应，他们表现出相应的离子性质.这与前面的分析是一致的，说明我们的计算数据虽然现在没有实验值对比，但是也是正确可靠的.

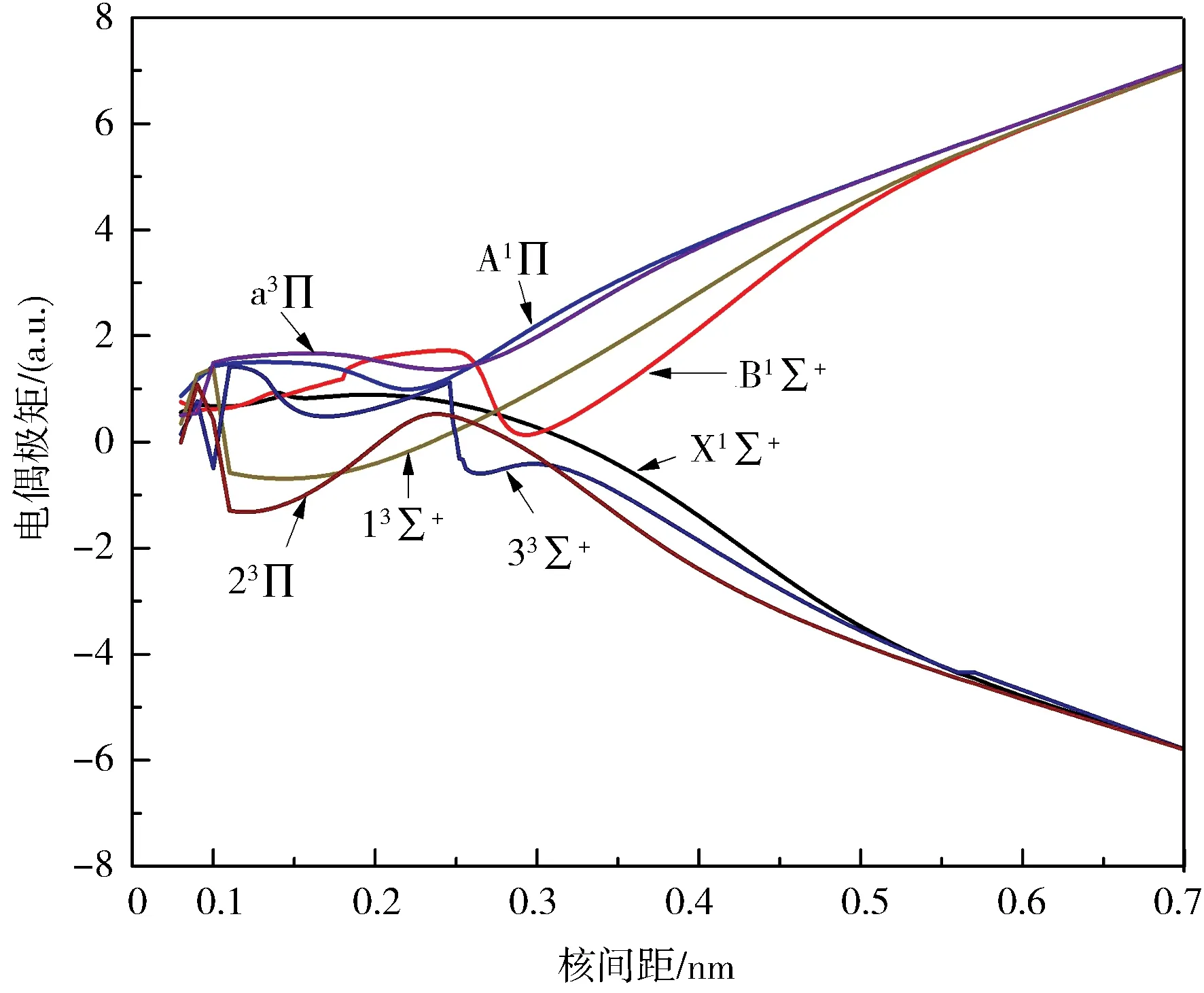
图2 BeB+离子7个电子态的电偶极矩Fig.2 The dipole moments for seven states of BeB+

根据跃迁选择定则计算了BeB+离子A1Π→Χ1Σ+、A1Π→B1Σ+、B1Σ+→Χ1Σ+、13Σ+→a3Π、23Π→13Σ+的跃迁偶极矩.跃迁偶极矩也是关于核间距的函数，其随核间距变化的曲线见图3.很清晰地看出，随着核间距的增加，A1Π→Χ1Σ+、A1Π→B1Σ+、B1Σ+→Χ1Σ+、13Σ+→a3Π和23Π→13Σ+跃迁偶极矩的函数值趋近于0，这是由于原子极限处的轨道禁止跃迁引起的.基于势能曲线和跃迁偶极矩，借助于Level 8.0程序，计算了最低5个电子态跃迁的爱因斯坦辐射系数Av′v″（单位为s-1）、弗兰克-康登因子f v′v″、总辐射速率Atotal（单位为s-1）和辐射寿命τ（单位为s）.B1Σ+由于具有双势阱结构，计算了第一个势阱，所有结果列于表3.可以看出，B1Σ+→Χ1Σ+与A1Π→Χ1Σ+相比，f v′v″小一些，这主要是由于B1Σ+与Χ1Σ+的平衡核间距差距更大，说明这2个态的波函数重叠较小，A1Π→B1Σ+跃迁的f v′v″是最大的，因为A1Π和B1Σ+的平衡核间距非常靠近，但是辐射寿命不具备足够短（10-6～10-8s），这表示并不能提供足够的激光冷却循环速率来产生自发辐射力.总的来说，这5个电子态跃迁的f v′v″都是很小的，不满足分子激光冷却的首要条件，即不具备高度对角化的f v′v″，所以都不具备激光冷却的可能性.

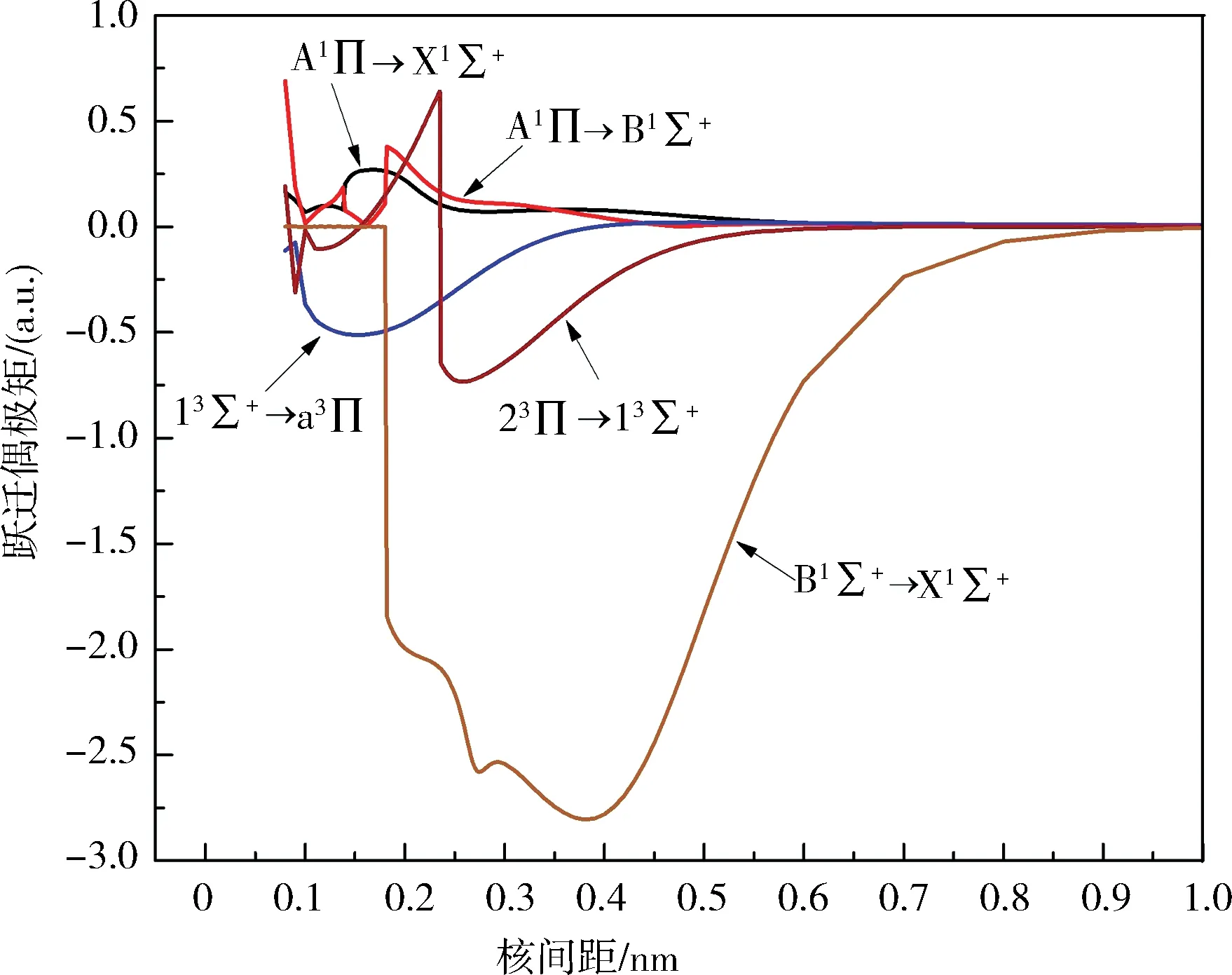
图3 BeB+离子的跃迁电偶极矩Fig.3 Transition dipole moments of BeB+

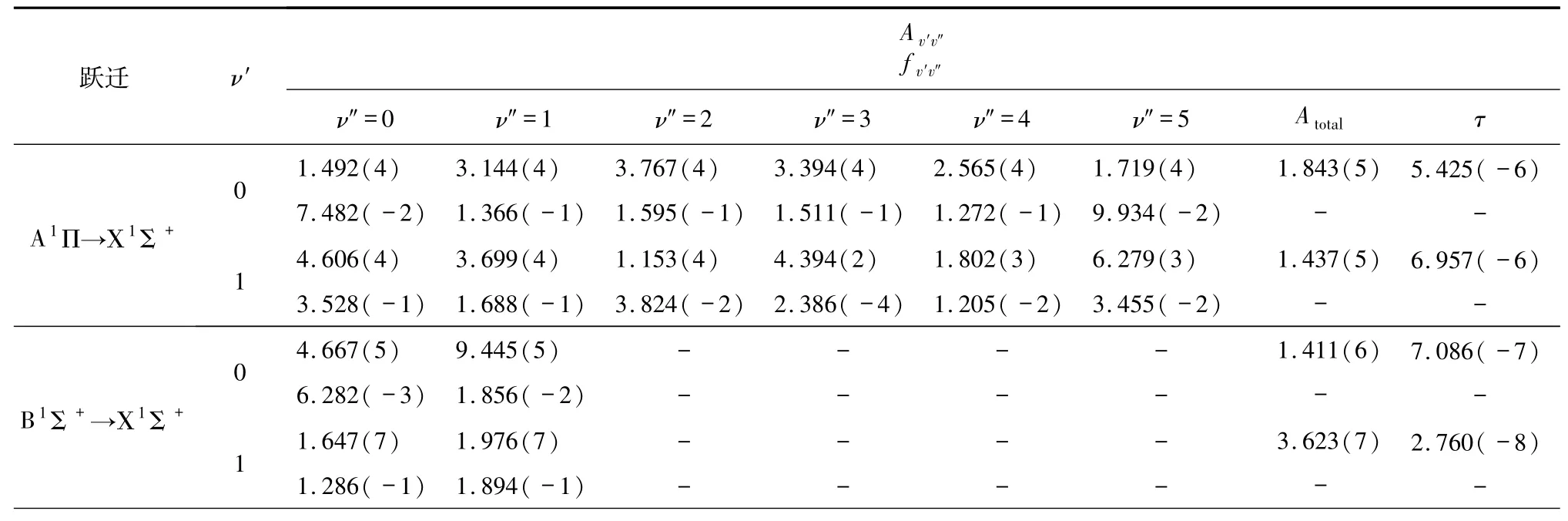
表3 A1Π→Χ1Σ+、B1Σ+→Χ1Σ+、13Σ+→a3Π跃迁的Av′v″、f v′v″、Atotal和τ值Tab.3 The Av′v″、f v′v″、Atotal andτof A1Π→Χ1Σ+、B1Σ+→Χ1Σ+and 13Σ+→a3Π

表 3（续）

3 结论

本文采用高精度多组态参考相互作用方法（MRCI），考虑Davidson修正（+Q）并结合相关一致基组aug-cc-pV5Z计算了BeB+离子前3个离解通道Be（1Sg）+B+（1Sg）、Be+（2Sg）+B（2Pu）、Be（3Pu）+B+（1Sg）对应的7个Λ-S态的势能曲线，继而通过LEVEL 8.0程序求解薛定谔方程得到7个Λ-S态的的光谱数据，最后根据计算的势能曲线、电偶极矩和跃迁偶极矩预测出BeB+离子最低5个电子态跃迁的爱因斯坦辐射系数Av′v″、弗兰克-康登因子f v′v″、总辐射速率Atotal和辐射寿命τ，发现这5个电子态跃迁的弗兰克-康登因子f v′v″都是很小的，不满足分子激光冷却的首要条件，所以都不具备激光冷却的可能性.

致谢宜宾学院计算物理四川省高等学校重点实验室开放课题基金（JSWL2018KFZ03）对本文给予了资助，谨致谢意.