单调变分不等式的改进次梯度外梯度算法
2021-03-15张双德夏福全
张双德, 夏福全, 黄 瑕
(四川师范大学 数学科学学院,四川成都610066)
设H是Hilbert空间,其内积和范数分别表示为〈·,·〉和‖·‖.变分不等式(VI)问题是求x*∈C,使得对∀x∈C,都有
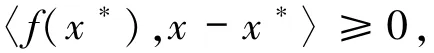
其中C是H中的一个非空闭凸子集,f:C→H是一个映射.变分不等式问题和它的解集分别用VI(C,f)和SOL(C,f)表示.变分不等式问题是优化理论中的一个基本问题,同时在结构分析、工程科学、经济科学、运筹学、自动控制等领域也具有广泛的应用[1-5].
为了解决变分不等式问题,Korpelevich[1]提出Rn空间中的外梯度算法(EG):

其中λ>0,PC是H→C的投影.在f是单调和Lipschitz连续且Lipschitz系数为的条件下,证明了算法所生成的序列收敛到解集中的一点.
在上述外梯度算法(EG)的每次迭代过程中,需要计算两次向C的投影,其中C是一个一般的非空闭凸集,这样的投影不容易实现.为了克服这个困难,Censor等[2]提出一种次梯度外梯度算法,该算法将(1)式中的投影换成向一个特殊结构的半空间Tk的投影:
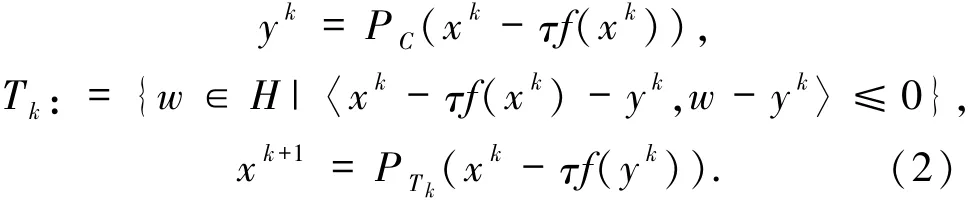
在映射f是单调和Lipschitz连续且Lipschitz系数为的条件下,证明了上述算法在Hilbert空间中的弱收敛性.接着,为了得到强收敛性,Censor等[6]又提出一种新的次梯度外梯度算法:

其中Tk与(2)式中相同.在f是单调和Lipschitz连续且Lipschitz系数为的条件下,证明了算法在Hilbert空间的强收敛性,但这个算法仍然需要计算一次向闭凸集C的投影,同时对映射f的Lipschitz系数的大小也有要求.
最近,He等[7]提出一种修正次梯度外梯度算法:

其中Tk与(2)式中相同.这个算法的两次投影均是向特殊结构的半空间投影,同时要求其中的βk满足恰当的线性搜索条件,从而不需要知道映射f的Lipschitz系数的大小,但只能得到该算法在Hilbert空间中的弱收敛结果.
受到文献[6-7]的启发,本文在文献[6]的基础上,将(3)式中向C的投影换成向文献[7]中的Ck投影,并选取与文献[7]相同的线性搜索条件,得到一种改进次梯度外梯度算法.当映射f满足单调和Lipschitz连续且Lipschitz系数大小未知的条件时,本文能得到该算法在Hilbert空间中的强收敛结果.同时,在算法迭代的过程中,只需要计算向特殊结构的半空间的投影,避免向一般闭凸集投影,计算更加容易.
1 预备知识
本节给出一些基本定义和引理.设H是Hilbert空间,C是H中的非空闭凸子集.{xk}强收敛到x记为xk→x,{xk}弱收敛到x记为xk⇀x.
定义1.1设C⊆H为非空闭凸子集,对∀x∈H,定义

为x在C上的投影.
定义1.2设凸函数c:H→R.c在x∈H处的次微分定义为

定义1.3设函数c:H→R.称c在x处是Gâteaux可微的,若x∈H,c′(x)∈H满足
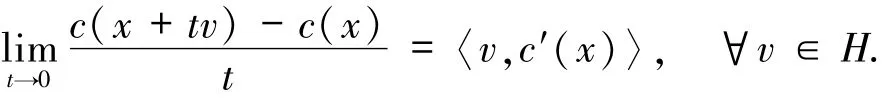
记c′(x)为c在x处的Gâteaux导数.
定义1.4设函数c:H→R,称c在x处是弱下半连续的,若xk弱收敛于x时有
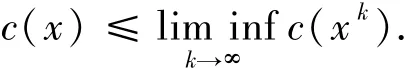
定义1.5设映射f:H→H,称f是
1)Lipschitz连续的,若存在L>0使得

2)单调的,若
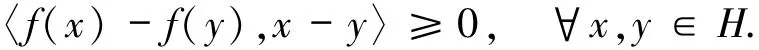
定义1.6设C⊆H,则C在v∈C处的法锥NC(v)定义为
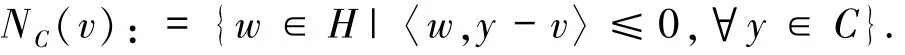
定义1.7设是H上的集值映射,则T是极大单调算子当且仅当满足
1)T是单调的即〈u-v,x-y〉≥0,∀u∈T(x),v∈T(y);
2)T的图像G(T):={(x,u)∈H×H|u∈T(x)}不包含于任何其他的单调算子的图像中.
引理1.1[8]设f:C→H是Lipschitz连续单调算子,定义
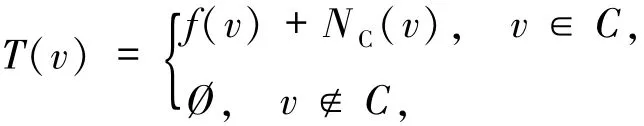
则T是极大单调算子.并且0∈Tv当且仅当v∈SOL(C,f).
引理1.2[9]任何Hilbert空间都具有Kadec-Klee性质,即是在H空间中的序列{xk}∞k=0,如果满足xk⇀x且‖xk‖→‖x‖,则有‖xk-x‖→0.
引理1.3[10]设凸函数c:H→R,则c在H上是下半连续的当且仅当c在H是弱下半连续的.
引理1.4[10]设凸函数c:H→R.如果c在x处是Gâteaux可微和次可微的,则有∂c(x)={c′(x)}.
引理1.5[11]设D⊆H为非空闭凸子集,则对∀x∈H,y∈D,有
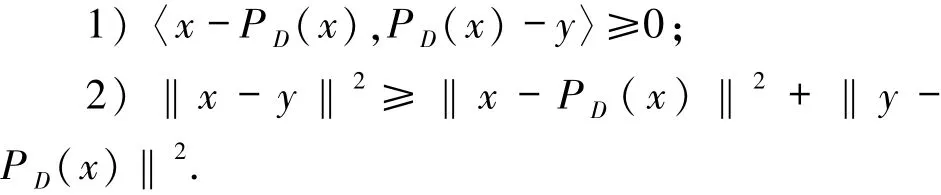
引理1.6[12]假设VI(C,f)的解集SOL(C,f)非空,x*∈C,则当x*∈SOL(C,f)时有以下2个条件的一个成立.
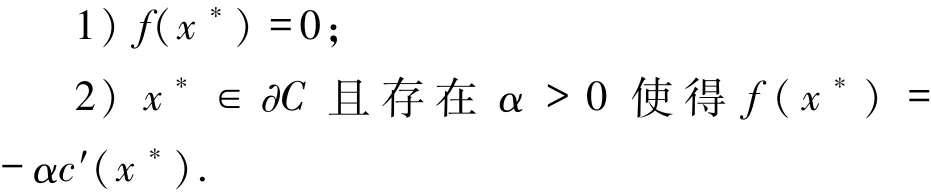
2 算法及收敛性分析
在本节中,非空闭凸集C定义为
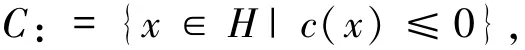
其中c:H→R是一个凸函数.同时在本文中,总假设下列条件满足:
条件2.1变分不等式VI(C,f)的解集SOL(C,f)非空.
条件2.2f:H→H是单调和Lipschitz连续的映射.
条件2.3函数c:H→R满足以下条件:
1)c(x)是凸函数;
2)c(x)在H上是下半连续的;
3)c(x)在H上Gâteaux可微的,且c′(x)在H上是M1-Lipschitz连续映射;
4)存在M2>0使得‖f(x)‖≤M2‖c′(x)‖,∀x∈∂C,∂C是C的边界.
注1条件2.3来源于文献[7],这是为了给出算法中的线性搜索条件,同时在算法的收敛性证明过程中也有重要作用.
算法2.1(改进次梯度外梯度算法)
步0:∀x0∈H,令k=0.
步1:构造半空间

计算

这里的βk=σρm k,σ>0,ρ∈(0,1).mk为满足下式的最小正整数:

其中M=M1M2,ν∈(0,1).
步2:构造半空间
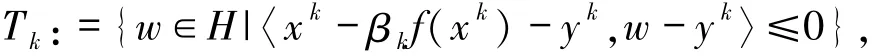
计算

步3:令
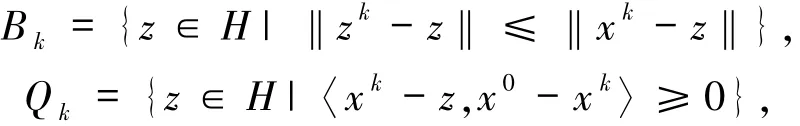
计算

步4:令k=k+1返回步1.
注2算法中Bk和Qk的构造来源于文献[4],与文献[5]相比这样做的好处在于只增加一次向超平面交的投影就能得到算法的强收敛性结果.
注3在算法2.1中,对任意的x∈C,都有

因此C⊆Ck.
又根据引理1.5和yk=PC k(xk-βkf(xk))有因此Ck⊆Tk.

为了证明算法2.1的收敛性,首先必须证明下面的引理.
引理2.1假设条件2.1-2.3成立.则由算法2.1生成的序列有界.
证明对所有的k≥0,容易看出Bk和Qk是闭凸集.再根据Qk的定义可得


因此

再由条件2.2有

因此

为了证明u∈Bk,即‖zk-u‖2≤‖xk-u‖2,下面分两种情况讨论:
情况1f(u)=0,则有
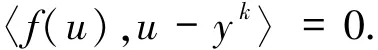
因此

根据Tk的定义和tk∈Tk有
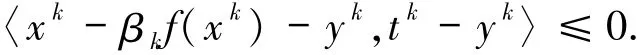
因此
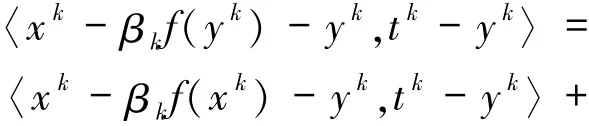
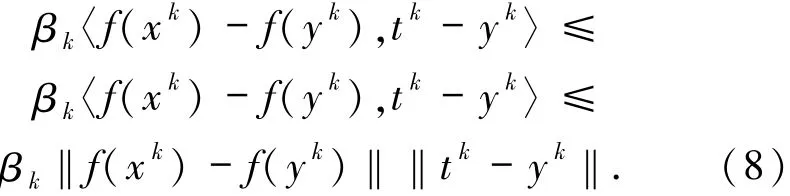
将(8)式代入(7)式中可得
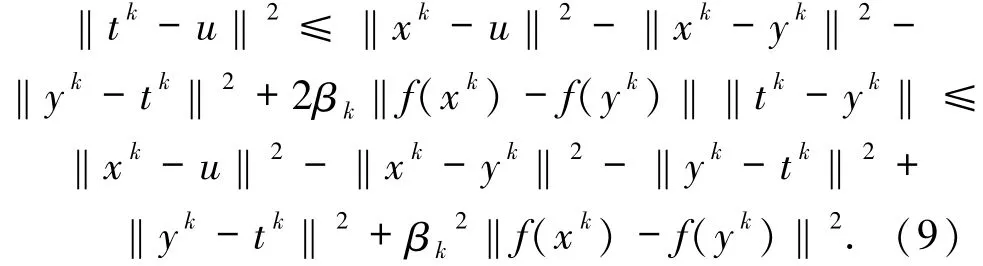
又根据(4)式可得
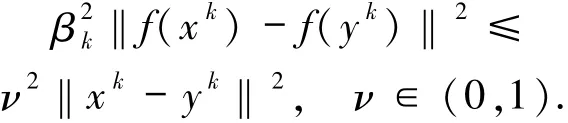
因此(9)式可化为

情况2f(u)≠0.根据引理1.6可知,存在α>0,使得f(u)=-αc′(u).由次微分不等式
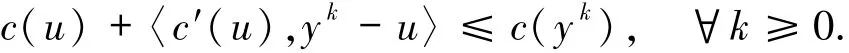
u∈∂C,c(u)=0可得
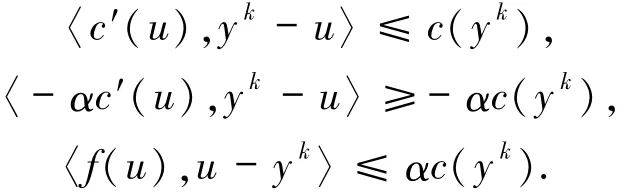
又因为yk∈Ck,即
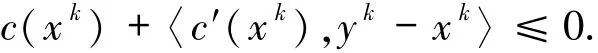
c′(x)在H上可微
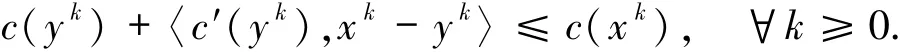
上两式相加可得

再根据条件2.3有

将(11)式代入(6)式中可得

将(8)式代入(12)式中可得
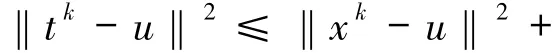

根据(4)式可将(13)式化简为
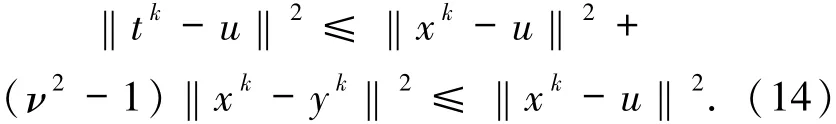
与情况1所得的不等式相同.再由zk的定义可知

将(10)式(或(14)式)代入(15)式中可得

根据(16)式以及Bk的定义可知u∈Bk,∀k>0.
下面利用归纳法证明u∈Bk∩Qk.
当n=0,Q0=H.则u∈B0∩Q0=B0,显然成立.
当n=k时,关系式成立,即u∈Bk∩Qk.下面去证明u∈Bk+1∩Qk+1成立.
由算法可知xk+1=PB k∩Q k(x0),因此有
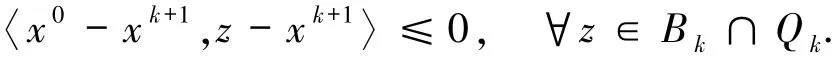
令z=u∈Bk∩Qk,则

因此u∈Qk+1,u∈Bk+1∩Qk+1.即u∈SOL(C,f)⊂Bk∩Qk,∀k>0.令u*=PSOL(C,f)(x0),因为u*∈SOL(C,f)⊂Bk∩Qk,xk+1=PB k∩Q k(x0).因此

定理2.1假设条件2.1-2.3成立.则由算法2.1生成的2个序列强收敛到SOL(C,f)中的一点u*,并且

证明首先条件2.1-2.3满足,则有引理2.1成立,即有界,易得也有界.由(5)式和xk+1∈Qk可得

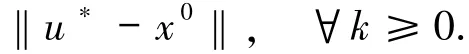
利用引理1.5和(5)式,令D=Qk,x=x0,y=xk+1可得

令k→∞,则有

又因为xk+1∈Bk,即
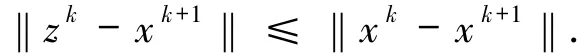
由三角不等式可得
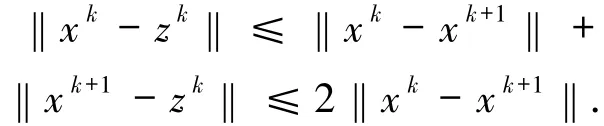
因此
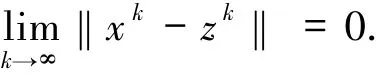
由(16)式可知

即

其中αk,ν∈(0,1),令k→∞,则有
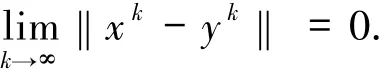
由条件2.2可知

在情况1中,由(9)式有

在情况2中,由(13)式有


又根据(4)式可得

将上式代入(19)式中可得到与(18)式相同的不等式.

再由(15)式有

结合上两式有

因此

其中αk,βk∈(0,1).令k→∞,则有
由三角不等式
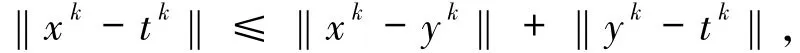
因此

下面首先证明x*∈C.根据yk∈Ck和Ck的定义可知

因此

由条件2.3的3)可知,c′(x)在H的任意有界子集上是有界的,即存在M′>0使得‖c′(xk)‖≤M′,∀k≤0.因此

又由条件2.3的2)可知c是下半连续的,根据定义1.4和引理1.3得

因此x*∈C.接下来证明x*∈SOL(C,f).令(v,w)∈G(T),由引理1.1则有w∈T(v)=f(v)+NC(v),因此
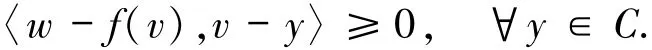
令y=x*,则有

又由yk=PC k(xk-βkf(xk)),因此

即

因此
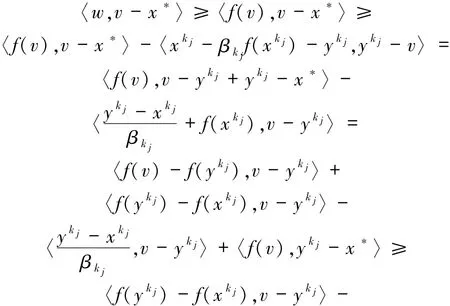

最后一个不等式根据f的单调性得出.
由于xk j⇀x*,则根据(17)式可知yk j⇀x*.在(20)式中令j→∞可得

因为T是极大单调算子,因此x*∈T-1(0)=SOL(C,f).由定理已知条件u*=PSOL(C,f)(x0),
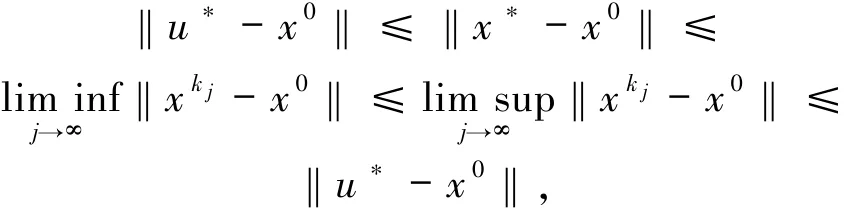
因此

即‖xk j-x0‖→‖x*-x0‖,且xk j-x0⇀x*-x0.则根据引理1.2可得‖xk j-x*‖→0.
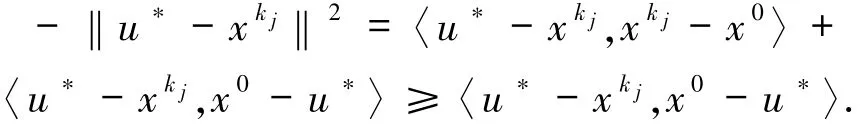
令j→∞可得

因此

假设xk强收敛到u*不成立,则一定存在ε>0和子序列使得
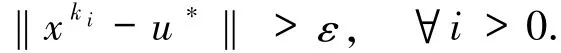
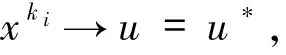
这与假设矛盾,因此xk→u*.
3 数值结果
在这部分内容中,利用例4.1给出算法2.1的计算机检验结果,同时与文献[7]的中的算法2.4(MSubEGM)和文献[6]的中的算法2.6(Censor)做比较.这些结果是用Matlab在CPU型号为2.0 GB的笔记本电脑上运行的.在算法2.1和算法MSub-EGM中,均取σ=1,ρ=0.6,ν=0.8,M=0.2,αk=0.4.在算法Censor中,取τ=0.4,αk=0.4.用iter来记迭代的步数,CPU来记运行所花费的时间,算法的终止条件为‖xk-yk‖≤ε.
例3.1定义

其中

初始点x0=(0,…,0).
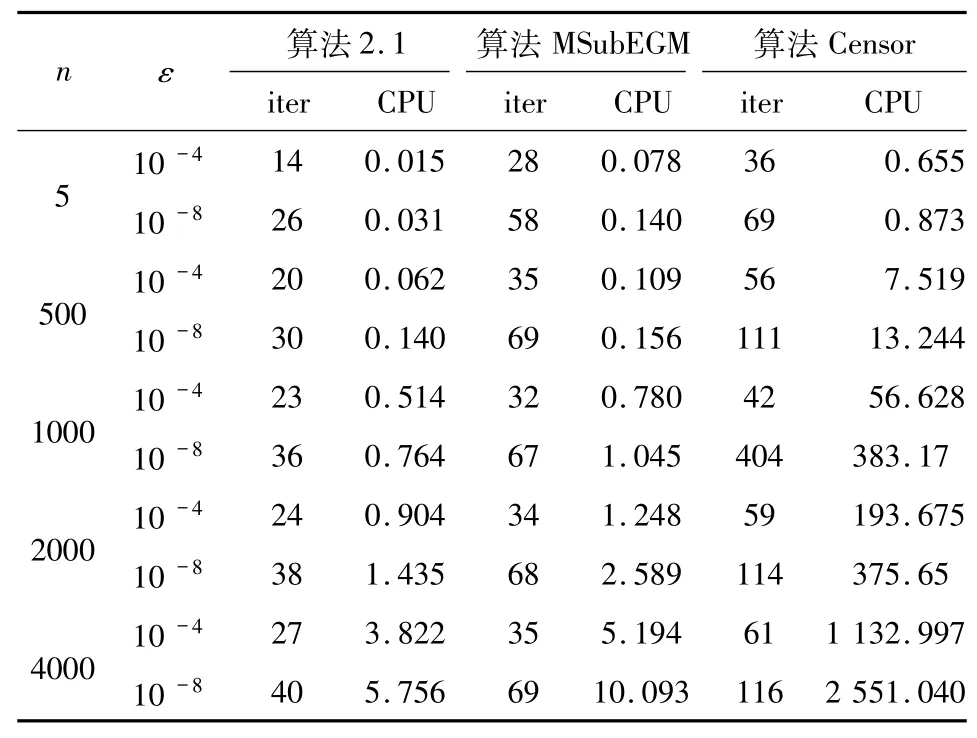
表1 例3.1的数值结果Tab.1 Numerical results of Example 3.1
